Published online by Cambridge University Press: 26 May 2017
Image inpainting methods recover true images from partial noisy observations. Natural images usually have two layers consisting of cartoons and textures. Methods using simultaneous cartoon and texture inpainting are popular in the literature by using two combined tight frames: one (often built from wavelets, curvelets or shearlets) provides sparse representations for cartoons and the other (often built from discrete cosine transforms) offers sparse approximation for textures. Inspired by the recent development on directional tensor product complex tight framelets (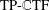 $\text{TP}\text{-}\mathbb{C}\text{TF}$s) and their impressive performance for the image denoising problem, we propose an iterative thresholding algorithm using tight frames derived from
$\text{TP}\text{-}\mathbb{C}\text{TF}$s) and their impressive performance for the image denoising problem, we propose an iterative thresholding algorithm using tight frames derived from 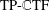 $\text{TP}\text{-}\mathbb{C}\text{TF}$s for the image inpainting problem. The tight frame
$\text{TP}\text{-}\mathbb{C}\text{TF}$s for the image inpainting problem. The tight frame 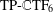 $\text{TP}\text{-}\mathbb{C}\text{TF}_{6}$ contains two classes of framelets; one is good for cartoons and the other is good for textures. Therefore, it can handle both the cartoons and the textures well. For the image inpainting problem with additive zero-mean independent and identically distributed Gaussian noise, our proposed algorithm does not require us to tune parameters manually for reasonably good performance. Experimental results show that our proposed algorithm performs comparatively better than several well-known frame systems for the image inpainting problem.
$\text{TP}\text{-}\mathbb{C}\text{TF}_{6}$ contains two classes of framelets; one is good for cartoons and the other is good for textures. Therefore, it can handle both the cartoons and the textures well. For the image inpainting problem with additive zero-mean independent and identically distributed Gaussian noise, our proposed algorithm does not require us to tune parameters manually for reasonably good performance. Experimental results show that our proposed algorithm performs comparatively better than several well-known frame systems for the image inpainting problem.