Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wu, Hualong
Gan, Jianzhou
Zhao, Bo
Gao, Wei
Guirao, Juan L.G.
and
Gao, Wei
2017.
On the computation of degree and distance mixing indices of Harary graphs and coronene polycyclic aromatic hydrocarbons.
Journal of Intelligent & Fuzzy Systems,
Vol. 33,
Issue. 5,
p.
3123.
Wu, Hualong
Zhao, Bo
Gan, Jianhou
and
Gao, Wei
2017.
Distance and indices computation in chains and nanotubes model as graph discrete dynamica systems.
Journal of Difference Equations and Applications,
Vol. 23,
Issue. 1-2,
p.
110.
Ahmad, Haseeb
Hussain, Muhammad
Nazeer, Waqas
and
Chu, Yu‐Ming
2020.
Distance‐based invariants of zigzag polyhex nanotube.
Mathematical Methods in the Applied Sciences,
Wang, Guangfu
and
Liu, Yajing
2020.
The edge-Wiener index of zigzag nanotubes.
Applied Mathematics and Computation,
Vol. 377,
Issue. ,
p.
125191.
Theresal, Santiagu
Xavier, Antony
and
Raja, S. Maria Jesu
2021.
Induced H-packing k-partition problem in certain carbon based nanostructures.
Journal of Mathematical Chemistry,
Vol. 59,
Issue. 6,
p.
1429.
Wang, Ying
Yousaf, Shamaila
Bhatti, Akhlaq Ahmad
and
Aslam, Adnan
2022.
Analyzing the expressions for nanostructures via topological indices.
Arabian Journal of Chemistry,
Vol. 15,
Issue. 1,
p.
103469.
Maria Jesu Raja, S.
and
Gracybaby, A.
2022.
Excessive Index of Certain Carbon Based Nanotubes.
Polycyclic Aromatic Compounds,
Vol. 42,
Issue. 6,
p.
3036.
Wang, Guangfu
Liu, Yajing
Wei, Jianxin
and
Liu, Jia-Bao
2023.
The Edge-Hyper-Wiener Index of Zigzag Single-Walled Nanotubes.
Polycyclic Aromatic Compounds,
Vol. 43,
Issue. 2,
p.
1509.


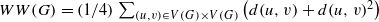 , where
, where 