Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T07:28:50.328Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGH ORDER EXPLICIT SECOND DERIVATIVE METHODS WITH STRONG STABILITY PROPERTIES BASED ON TAYLOR SERIES CONDITIONS

Part of: Numerical analysis: Ordinary differential equations

Published online by Cambridge University Press:  23 September 2022

A. MORADI Open the ORCID record for A. MORADI [Opens in a new window] ,
A. ABDI Open the ORCID record for A. ABDI [Opens in a new window]  and
G. HOJJATI Open the ORCID record for G. HOJJATI [Opens in a new window]
A. MORADI
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: [email protected], [email protected].
A. ABDI*
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: [email protected], [email protected]. Research Department of Computational Algorithms and Mathematical Models, University of Tabriz, Tabriz, Iran.
G. HOJJATI
Affiliation:
Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran; e-mail: [email protected], [email protected]. Research Department of Computational Algorithms and Mathematical Models, University of Tabriz, Tabriz, Iran.
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When faced with the task of solving hyperbolic partial differential equations (PDEs), high order, strong stability-preserving (SSP) time integration methods are often needed to ensure preservation of the nonlinear strong stability properties of spatial discretizations. Among such methods, SSP second derivative time-stepping schemes have been recently introduced and used for evolving hyperbolic PDEs. In previous works, coupling of forward Euler and a second derivative formulation led to sufficient conditions for a second derivative general linear method (SGLM), which preserve the strong stability properties of spatial discretizations. However, for such methods, the types of spatial discretizations that can be used are limited. In this paper, we use a formulation based on forward Euler and Taylor series conditions to extend the SSP SGLM framework. We investigate the construction of SSP second derivative diagonally implicit multistage integration methods (SDIMSIMs) as a subclass of SGLMs with order 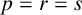$p=r=s$ and stage order 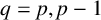$q=p,p-1$ up to order eight, where r is the number of external stages and s is the number of internal stages of the method. Proposed methods are examined on some one-dimensional linear and nonlinear systems to verify their theoretical order, and show potential of these schemes in preserving some nonlinear stability properties such as positivity and total variation.

Keywords

second derivative methodsmonotonicitystrong stability preservingTaylor seriesEuler equation

MSC classification

Primary: 65L05: Initial value problems
Type
Research Article
Information
The ANZIAM Journal , Volume 64 , Issue 3 , July 2022 , pp. 264 - 291
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdi, A., “Construction of high-order quadratically stable second-derivative general linear methods for the numerical integration of stiff ODEs”, J. Comput. Appl. Math. 303 (2016) 218–228; doi:10.1016/j.cam.2016.02.054.CrossRefGoogle Scholar
Abdi, A. and Behzad, B., “Efficient Nordsieck second derivative general linear methods: construction and implementation”, Calcolo 55 (2018) Article Id 28, 1–16; doi:10.1007/s10092-018-0270-7.CrossRefGoogle Scholar
Abdi, A., Braś, M. and Hojjati, G., “On the construction of second derivative diagonally implicit multistage integration methods”, Appl. Numer. Math. 76 (2014) 1–18; doi:10.1016/j.apnum.2013.08.006.CrossRefGoogle Scholar
Abdi, A. and Conte, C., “Implementation of second derivative general linear methods”, Calcolo 57 (2020) 1–29; doi:10.1007/s10092-020-00370-w.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “An extension of general linear methods”, Numer. Algorithms 57 (2011) 149–167; doi:10.1007/s11075-010-9420-y.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “Maximal order for second derivative general linear methods with Runge–Kutta stability”, Appl. Numer. Math. 61 (2011) 1046–1058; doi:10.1016/j.apnum.2011.06.004.CrossRefGoogle Scholar
Abdi, A. and Hojjati, G., “Implementation of Nordsieck second derivative methods for stiff ODEs”, Appl. Numer. Math. 94 (2015) 241–253; doi:10.1016/j.apnum.2015.04.002.CrossRefGoogle Scholar
Balsara, D. S. and Shu, C.-W., “Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy”, J. Comput. Phys. 160 (2000) 405–452; doi:10.1006/jcph.2000.6443.CrossRefGoogle Scholar
Barghi Oskouie, N., Hojjati, G. and Abdi, A., “Efficient second derivative methods with extended stability regions for non-stiff IVPs”, Comput. Appl. Math. 37 (2018) 2001–2016; doi:10.1007/s40314-018-0619-1.CrossRefGoogle Scholar
Butcher, J. C., Numerical methods for ordinary differential equations (Wiley,New York, 2016).CrossRefGoogle Scholar
Butcher, J. C. and Hojjati, G., “Second derivative methods with RK stability”, Numer. Algorithms 40 (2005) 415–429; doi:10.1007/s11075-005-0413-1.CrossRefGoogle Scholar
Califano, G., Izzo, G. and Jackiewicz, Z., “Strong stability preserving general linear methods with Runge–Kutta stability”, J. Sci. Comput. 76 (2018) 943–968; doi:10.1007/s10915-018-0646-5.CrossRefGoogle Scholar
Christlieb, A. J., Gottlieb, S., Grant, Z. and Seal, D. C., “Explicit strong stability preserving multistage two-derivative time-stepping schemes”, J. Sci. Comput. 68 (2016) 914–942; doi:10.1007/s10915-016-0164-2.CrossRefGoogle Scholar
Cockburn, B. and Shu, C.-W., “TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework”, Math. Comput. 52 (1989) 411–435; doi:10.2307/2008474.Google Scholar
Constantinescu, E. M. and Sandu, A., “Optimal explicit strong-stability-preserving general linear methods”, SIAM J. Sci. Comput. 32 (2010) 3130–3150; doi:10.1137/090766206.CrossRefGoogle Scholar
Ditkowski, A., Gottlieb, S. and Grant, Z. J., “Two-derivative error inhibiting schemes and enhanced error inhibiting schemes”, SIAM J. Numer. Anal. 58 (2020) 3197–3225; doi:10.1137/19M1306129.CrossRefGoogle Scholar
Ezzeddine, A. K., Hojjati, G. and Abdi, A., “Sequential second derivative general linear methods for stiff systems”, Bull. Iranian Math. Soc. 40 (2014) 83–100.Google Scholar
Ferracina, L. and Spijker, M. N., “Stepsize restrictions for total-variation-boundedness in general Runge–Kutta procedures”, Appl. Numer. Math. 53 (2005) 265–279; doi:10.1016/j.apnum.2004.08.024.CrossRefGoogle Scholar
Gottlieb, S., “On high order strong stability preserving Runge–Kutta and multi step time discretizations”, J. Sci. Comput. 25 (2005) 105–128; doi:10.1007/BF02728985.Google Scholar
Gottlieb, S., Ketcheson, D. I. and Shu, C.-W., Strong stability preserving Runge–Kutta and multistep time discretizations (World Scientific,Hackensack, 2011).CrossRefGoogle Scholar
Gottlieb, S., Shu, C.-W. and Tadmor, E., “Strong stability-preserving high-order time discretization methods”, SIAM Rev. 43 (2001) 89–112; doi:10.1137/S003614450036757X.CrossRefGoogle Scholar
Grant, Z., Gottlieb, S. and Seal, D. C., “A strong stability preserving analysis for explicit multistage two-derivative time-stepping schemes based on Taylor series conditions”, Commun. Appl. Math. Comput. 1 (2019) 21–59; doi:10.1007/s42967-019-0001-3.Google Scholar
Hesthaven, J., Gottlieb, S. and Gottlieb, D., Spectral methods for time dependent problems, Volume 21 of Cambridge Monographs of Applied and Computational Mathematics (Cambridge University Press,Cambridge, 2007).CrossRefGoogle Scholar
Higueras, I., “Representations of Runge–Kutta methods and strong stability preserving methods”, SIAM J. Numer. Anal. 43 (2005) 924–948; doi:10.1137/S0036142903427068.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R., Topics in matrix analysis (Cambridge University Press,Cambridge, 1991).CrossRefGoogle Scholar
Hundsdorfer, W. and Ruuth, S. J., “On monotonicity and boundedness properties of linear multistep methods”, Math. Comput. 75 (2005) 655–672; doi:10.1090/S0025-5718-05-01794-1.CrossRefGoogle Scholar
Izzo, G. and Jackiewicz, Z., “Strong stability preserving general linear methods”, J. Sci. Comput. 65 (2015) 271–298; doi:10.1007/s10915-014-9961-7.CrossRefGoogle Scholar
Izzo, G. and Jackiewicz, Z., “Strong stability preserving multistage integration methods”, Math. Model. Anal. 20 (2015) 552–577; doi:10.3846/13926292.2015.1085921.CrossRefGoogle Scholar
Izzo, G. and Jackiewicz, Z., “Strong stability preserving transformed DIMSIMs”, J. Comput. Appl. Math. 343 (2019) 174–188; doi:10.1016/j.cam.2018.03.018.CrossRefGoogle Scholar
Jiang, G.-S. and Shu, C.-W., “Efficient implementation of weighted ENO schemes”, J. Comput. Phys. 126 (1996) 202–228; doi:10.1006/jcph.1996.0130.CrossRefGoogle Scholar
Ketcheson, D. I., Gottlieb, S. and Macdonald, C. B., “Strong stability preserving two-step Runge–Kutta methods”, SIAM J. Numer. Anal. 49 (2011) 2618–2639; doi:10.1137/10080960X.CrossRefGoogle Scholar
Laney, C., Computational gasdynamics (Cambridge University Press,Cambridge, 1998).CrossRefGoogle Scholar
LeVeque, R. J., Finite volume methods for hyperbolic problems (Cambridge University Press,Cambridge, 2002).CrossRefGoogle Scholar
Moradi, A., Abdi, A. and Farzi, J., “Strong stability preserving second derivative diagonally implicit multistage integration methods”, Appl. Numer. Math. 150 (2020) 536–558; doi:10.1016/j.apnum.2019.11.001.CrossRefGoogle Scholar
Moradi, A., Abdi, A. and Farzi, J., “Strong stability preserving second derivative general linear methods with Runge–Kutta stability”, J. Sci. Comput. 85 (2020) Article Id 1, 1–39; doi:10.1007/s10915-020-01306-w.CrossRefGoogle Scholar
Moradi, A., Farzi, J. and Abdi, A., “Strong stability preserving second derivative general linear methods”, J. Sci. Comput. 81 (2019) 392–435; doi:10.1007/s10915-019-01021-1.CrossRefGoogle Scholar
Moradi, A., Farzi, J. and Abdi, A., “Order conditions for second derivative general linear methods”, J. Comput. Appl. Math. 387 (2021) Article Id 112488, 1–16; doi:10.1016/j.cam.2019.112488.CrossRefGoogle Scholar
Moradi, A., Sharifi, M. and Abdi, A., “Transformed implicit-explicit second derivative diagonally implicit multistage integration methods with strong stability preserving explicit part”, Appl. Numer. Math. 156 (2020) 14–31; doi:10.1016/j.apnum.2020.04.007.CrossRefGoogle Scholar
Qiu, J. X. and Shu, C. W., “Finite difference WENO schemes with Lax–Wendroff-type time discretizations”, SIAM J. Sci. Comput. 24 (2003) 2185–2198; doi:10.1137/S1064827502412504.CrossRefGoogle Scholar
Ramazani, P., Abdi, A., Hojjati, G. and Moradi, A., “Explicit Nordsieck second derivative general linear methods for ODEs”, ANZIAM J. 64 (2022) 69–88; doi:10.1017/S1446181122000049.Google Scholar
Spijker, M. N., “Stepsize conditions for general monotonicity in numerical initial value problems”, SIAM J. Numer. Anal. 45 (2007) 1226–1245; doi:10.1137/060661739.CrossRefGoogle Scholar
Sweby, P. K., “High resolution schemes using flux limiters for hyperbolic conservation laws”, SIAM J. Numer. Anal. 21 (1984) 995–1011; doi:10.1137/0721062.CrossRefGoogle Scholar
Toro, E. F., Riemann solvers and numerical methods for fluid dynamics, 3rd edn (Springer,Berlin–Heidelberg, 2009).CrossRefGoogle Scholar