Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T11:59:05.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Green's function of the clamped punctured disk

Published online by Cambridge University Press:  17 February 2009

Mitsuru Nakai  and
Leo Sario
Mitsuru Nakai
Affiliation:
Department of Mathematics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Japan
Leo Sario
Affiliation:
Department of Mathematics, University of California, Los Angeles, California, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If a thin elastic circular plate B: ∣z∣ < 1 is clamped (simply supported, respectively) along its edge ∣z∣ = 1, its deflection at z ∈ B under a point load at ζ ∈ B, measured positively in the direction of the gravitational pull, is the biharmonic Green's function β(z, ζ) of the clamped plate (γ(z, ζ) of the simply supported plate, respectively). We ask: how do β(z, ζ) and γ(z, ζ) compare with the corresponding deflections β0(z, ζ) and γ0(z, ζ) of the punctured circular plate B0: 0 < ∣ z ∣ < 1 that is “clamped” or “simply supported”, respectively, also at the origin? We shall show that γ(z, ζ) is not affected by the puncturing, that is, γ(·, ζ) = γ0(·, ζ), whereas β(·, ζ) is:

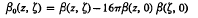
on B0 × B0. Moreover, while β((·, ζ) is of constant sign, β0(·, ζ) is not. This gives a simple counterexmple to the conjecture of Hadamard [6] that the deflection of a clampled thin elastic plate be always of constant sign:

The biharmonic Gree's function of a clampled concentric circular annulus is not of constant sign if the radius of the inner boundary circle is sufficiently small.

Earlier counterexamples to Hadamard's conjecture were given by Duffin [2], Garabedian [4], Loewner [7], and Szegö [9]. Interest in the problem was recently revived by the invited address of Duffin [3] before the Annual Meeting of the American Mathematical Society in 1974. The drawback of the counterexample we will present is that, whereas the classical examples are all simply connected, ours is not. In the simplicity of the proof, however, there is no comparison.

Type
Research Article
Information
The ANZIAM Journal , Volume 20 , Issue 2 , December 1977 , pp. 175 - 181
Copyright
Copyright © Australian Mathematical Society 1977

References

REFERENCES

[1]Bergman, S. and Schiffer, M., Kernel functions and elliptic differential equations in mathematical physics. (Academic Press, New York, 1953, 432 pp.).Google Scholar
[2]Duffin, R. J., “On a question of Hadamard concerning super-biharmonic functions”, J. Math. Physics 27 (1949), 253–258.Google Scholar
[3]Duffin, R. J., “Some problems of mathematics and science”, Bull. Amer. Math. Soc. 80 (1974), 1053–1070.Google Scholar
[4]Garabedian, P. R., “A partial differential equation arising in conformal mapping”, Pacific J. Math. 1 (1951), 485–524.CrossRefGoogle Scholar
[5]Garabedian, P. R., Partial differential equations. (Wiley, New York-London-Sydney, 1967, 672 pp.).Google Scholar
[6]Hadamard, J., “Mémoire sur le problème d'analyse relatif à l'équilibre des plaques élastiques encastrées”, Mémoires présentés par divers savants étrangers à l'Académie des Sciences, 33 (1908), 515–629.Google Scholar
[7]Loewner, C., “On generalization of solutions of the biharmonic equation in the plane by conformal mapping”, Pacific J. Math. 3 (1953), 417–436.CrossRefGoogle Scholar
[8]Nakai, M. and Sario, L., “A strict inclusion related to biharmonic Green's functions of clamped and simply supported bodies”, Ann. Acad. Sci. Fenn. A.I.3, 1977, 53–58.CrossRefGoogle Scholar
[9]Szegö, G., “Remark on the preceding paper by Charles Loewner”, Pacific J. Math. 3 (1953), 437–446.CrossRefGoogle Scholar