Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Yuji
and
Ge, Weigao
2003.
Asymptotic behavior of certain delay differential equations with forcing term.
Journal of Mathematical Analysis and Applications,
Vol. 280,
Issue. 2,
p.
350.
Liu, Yuji
and
Ge, Weigao
2004.
Stability theorems and existence results for periodic solutions of nonlinear impulsive delay differential equations with variable coefficients.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 57,
Issue. 3,
p.
363.
Liu, Yuji
and
Ge, Weigao
2004.
Global asymptotic behavior of solutions of a forced delay difference equation.
Computers & Mathematics with Applications,
Vol. 47,
Issue. 8-9,
p.
1211.
Qian, Chuanxi
and
Sun, Yijun
2007.
Global attractivity of solutions of nonlinear delay differential equations with a forcing term.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 66,
Issue. 3,
p.
689.
Benhammouda, Brahim
and
Vazquez-Leal, Hector
2016.
A new multi-step technique with differential transform method for analytical solution of some nonlinear variable delay differential equations.
SpringerPlus,
Vol. 5,
Issue. 1,
GÖKMEN, Elçin
and
SEZER, Mehmet
2020.
A MODIFIED TAYLOR COLLOCATION METHOD FOR PANTOGRAPH TYPE FUNCTIONAL DIFFERENTIAL EQUATIONS WITH HYBRID PROPORTIONAL AND VARIABLE DELAYS.
Mugla Journal of Science and Technology,
Vol. 6,
Issue. 1,
p.
1.
GÜRBÜZ, Burcu
2020.
A novel method for solving a class of functional differential equations.
Balıkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi,
Vol. 22,
Issue. 1,
p.
66.


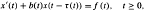
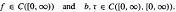
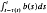 is asymptotically constant.
is asymptotically constant.