We study the equation

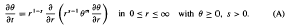
Here s is not necessarily integral; m is initially unrestricted. Material-conserving instantaneous source solutions of A are reviewed as an entrée to material-losing solutions. Simple physical arguments show that solutions for a finite slug losing material at infinity at a finite nonzero rate can exist only for the following m-ranges: 0 < s < 2, −2s−1 < m ≤ −1; s > 2, −1 < m < −2s−1. The result for s = 1 was known previously. The case s = 2, m = −1, needs further investigation. Three different similarity schemes all lead to the same ordinary differential equation. For 0 < s < 2, parameter γ (0 < γ < ∞) in that equation discriminates between the three classes of solution: class 1 gives the concentration scale decreasing as a negative power of (1 + t/T); 2 gives exponential decrease; and 3 gives decrease as a positive power of (1 − t/T), the solution vanishing at t = T < ∞. Solutions for s = 1, 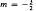are presented graphically. The variation of concentration and flux profiles with increasing γ is physically explicable in terms of increasing flux at infinity. An indefinitely large number of exact solutions are found for s = 1,γ = 1. These demonstrate the systematic variation of solution properties as m decreases from −1 toward −2 at fixed γ.