Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bäckdahl, Thomas
and
Valiente Kroon, Juan A.
2011.
The ‘non-Kerrness’ of domains of outer communication of black holes and exteriors of stars.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 467,
Issue. 2130,
p.
1701.
An, Zhongshan
2020.
Elliptic boundary value problems for the stationary vacuum spacetimes.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 1,
An, Zhongshan
2020.
Ellipticity of Bartnik Boundary Data for Stationary Vacuum Spacetimes.
Communications in Mathematical Physics,
Vol. 373,
Issue. 3,
p.
859.


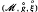 .
.