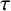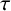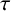1 Introduction
Over the past decade, there has been a growth of interest in transport equations in the form of hyperbolic reaction-diffusion partial differential equations (PDEs):
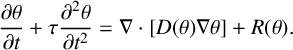 $$ \begin{align} \frac{\partial \theta}{\partial t}+\tau \frac{\partial^2 \theta}{\partial t^2}=\nabla\cdot[D(\theta)\nabla\theta]+R(\theta). \end{align} $$
$$ \begin{align} \frac{\partial \theta}{\partial t}+\tau \frac{\partial^2 \theta}{\partial t^2}=\nabla\cdot[D(\theta)\nabla\theta]+R(\theta). \end{align} $$
When
![]() $\tau =0$
, this equation is the extensively studied nonlinear reaction-diffusion equation of parabolic type. In standard physical applications that involve increasing entropy,
$\tau =0$
, this equation is the extensively studied nonlinear reaction-diffusion equation of parabolic type. In standard physical applications that involve increasing entropy,
![]() $D>0$
, except perhaps at
$D>0$
, except perhaps at
![]() $\theta =0$
where the equation might be degenerate with
$\theta =0$
where the equation might be degenerate with
![]() $D=0$
. In the case
$D=0$
. In the case
![]() $\tau>0$
, this equation is said to be a hyperbolic diffusion equation or a damped wave equation, depending on the application. Around 1870, Maxwell’s electromagnetic wave equation incorporated damping proportional to the conductivity of the medium [Reference Maxwell34]. In the following decade, Heaviside applied the linear telegraph equation [Reference Heaviside24] with a linear damping term to represent the decaying voltage as charge leaks between transmission lines that are separated by a dielectric medium (see for example, the review by Donaghy-Spargo [Reference Donaghy-Spargo16]). Unlike parabolic diffusion equations, hyperbolic diffusion equations predict a bounded speed of propagation of a local disturbance. For familiar irreversible transport phenomena of heat, with matter and charge obeying the second law of thermodynamics at the meso-scale, the unbounded propagation speed of a diffusion equation causes no practical problem. For example, the one-dimensional instantaneous point source solution of the linear diffusion equation is proportional to the Gaussian,
$\tau>0$
, this equation is said to be a hyperbolic diffusion equation or a damped wave equation, depending on the application. Around 1870, Maxwell’s electromagnetic wave equation incorporated damping proportional to the conductivity of the medium [Reference Maxwell34]. In the following decade, Heaviside applied the linear telegraph equation [Reference Heaviside24] with a linear damping term to represent the decaying voltage as charge leaks between transmission lines that are separated by a dielectric medium (see for example, the review by Donaghy-Spargo [Reference Donaghy-Spargo16]). Unlike parabolic diffusion equations, hyperbolic diffusion equations predict a bounded speed of propagation of a local disturbance. For familiar irreversible transport phenomena of heat, with matter and charge obeying the second law of thermodynamics at the meso-scale, the unbounded propagation speed of a diffusion equation causes no practical problem. For example, the one-dimensional instantaneous point source solution of the linear diffusion equation is proportional to the Gaussian,
![]() $t^{-1/2}\exp (-x^2/4Dt)$
. This diminishes so rapidly that at some finite distance from the source, the disturbance is so small that it is not physically measurable.
$t^{-1/2}\exp (-x^2/4Dt)$
. This diminishes so rapidly that at some finite distance from the source, the disturbance is so small that it is not physically measurable.
At very small time scales and micro-scale distances, at very low temperatures, and at very large time scales and astronomical distances, the bounded speed of propagation can be significant. In molecular materials, there is a short “collision time” delay
![]() $\tau $
before temperature gradients can lead to fluxes via intermolecular collisions. For neon gas at standard temperature and pressure, the standard formulae from kinetic theory for mean free path and mean kinetic energy [Reference Feynman, Leighton and Sands18] give
$\tau $
before temperature gradients can lead to fluxes via intermolecular collisions. For neon gas at standard temperature and pressure, the standard formulae from kinetic theory for mean free path and mean kinetic energy [Reference Feynman, Leighton and Sands18] give
![]() $\tau \approx 7\times 10^{-10}$
s and for monovalent metals,
$\tau \approx 7\times 10^{-10}$
s and for monovalent metals,
![]() $\tau \approx 10^{-14}$
s [Reference Maurer33]. Cattaneo [Reference Cattaneo11] modified the theory of heat conduction to a hyperbolic diffusion equation to partly account for the delay. The delayed heat flux under Fourier’s law is
$\tau \approx 10^{-14}$
s [Reference Maurer33]. Cattaneo [Reference Cattaneo11] modified the theory of heat conduction to a hyperbolic diffusion equation to partly account for the delay. The delayed heat flux under Fourier’s law is
![]() $J=-k(\theta )\nabla \theta (x,t-\tau )$
. Then by conservation of heat energy at density
$J=-k(\theta )\nabla \theta (x,t-\tau )$
. Then by conservation of heat energy at density
![]() $\mathcal E$
,
$\mathcal E$
,
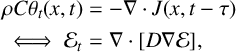 $$ \begin{align*} \rho C\theta_t(x,t)&=-\nabla\cdot J(x,t-\tau)\\ \iff \mathcal E_t&=\nabla\cdot[D\nabla \mathcal E], \end{align*} $$
$$ \begin{align*} \rho C\theta_t(x,t)&=-\nabla\cdot J(x,t-\tau)\\ \iff \mathcal E_t&=\nabla\cdot[D\nabla \mathcal E], \end{align*} $$
where
![]() $\rho $
is mass density,
$\rho $
is mass density,
![]() $\theta $
is absolute temperature, k is thermal conductivity, C is specific heat per unit mass and
$\theta $
is absolute temperature, k is thermal conductivity, C is specific heat per unit mass and
![]() $D=k/\rho C$
is thermal diffusivity. In the linear unidimensional model with constant transport coefficients,
$D=k/\rho C$
is thermal diffusivity. In the linear unidimensional model with constant transport coefficients,
![]() $\theta _t +\tau \theta _{tt}+O(\tau ^2)=D\theta _{xx}.$
In this equation, the spatial derivatives still occur within a self-adjoint operator, so that with homogeneous linear boundary conditions and smooth initial conditions, a series solution for
$\theta _t +\tau \theta _{tt}+O(\tau ^2)=D\theta _{xx}.$
In this equation, the spatial derivatives still occur within a self-adjoint operator, so that with homogeneous linear boundary conditions and smooth initial conditions, a series solution for
![]() $\theta (x,t)$
can be obtained as a trigonometric series after separation of variables.
$\theta (x,t)$
can be obtained as a trigonometric series after separation of variables.
Neglecting
![]() $O(\tau ^2)$
, wave-like solutions of this equation have a speed limit
$O(\tau ^2)$
, wave-like solutions of this equation have a speed limit
![]() $c=\sqrt {D/\tau }$
. By comparison theory, for hyperbolic diffusion with nonlinear bounded diffusivity function, the parameter D within this expression for the speed limit may be generalised to the least upper bound
$c=\sqrt {D/\tau }$
. By comparison theory, for hyperbolic diffusion with nonlinear bounded diffusivity function, the parameter D within this expression for the speed limit may be generalised to the least upper bound
![]() $D_{\max }$
. The delay
$D_{\max }$
. The delay
![]() $\tau $
may be much longer at very low temperatures. Tisza [Reference Tisza41] and Landau [Reference Landau30] gave alternative versions of “second sound” wave theory for the transport of heat in liquid helium.
$\tau $
may be much longer at very low temperatures. Tisza [Reference Tisza41] and Landau [Reference Landau30] gave alternative versions of “second sound” wave theory for the transport of heat in liquid helium.
At cosmological distances, relative to an inertial observer, material transport must be limited by the speed of light c. This can be achieved in a simple phenomenological model that is the hyperbolic diffusion equation [Reference Broadbridge, Kolesnik, Leonenko and Olenko10]. In some sense, the hyperbolic diffusion equation has been considered to be Lorentz invariant in three space and two time (
![]() $3+2$
) dimensions (see [Reference Ali and Zhang2]).
$3+2$
) dimensions (see [Reference Ali and Zhang2]).
Speed limits are naturally a consideration in modelling biological units, whether they be individual organisms or motile cells. Using the Chapman–Enskog expansion, Filbet et al. [Reference Filbet, Laurençot and Perthame19] derived hyperbolic models for chemotaxis, with a clear connection to parabolic models. Natalini et al. [Reference Natalini, Ribot and Twarogowska36] numerically compared degenerate parabolic and hyperbolic models for chemotaxis. Hernandez et al. [Reference Hernandez, Rincon, Herrera and Chavez25] developed a hyperbolic model for the movement of bacteria through a porous medium. In spatially dependent populations, individuals have a residence time in a home range of high population density before they decide to explore alternative regions of lower density. For example, if mobility of a fish population is modelled by diffusivity
![]() $D=$
100 km
$D=$
100 km
![]() $^2$
/yr and
$^2$
/yr and
![]() $\tau =0.02$
yr (one week), then the population wave has maximum speed 70 km/yr. This should not be considered to be a physical limit of instantaneous speed but as a practical longer-term limit due to hesitancy to migrate when the great majority consists of home-stayers compared with a minority of rangers [Reference Broadbridge, Hutchinson, Li and Mann9]. A reaction term then represents the reproduction of the species.
$\tau =0.02$
yr (one week), then the population wave has maximum speed 70 km/yr. This should not be considered to be a physical limit of instantaneous speed but as a practical longer-term limit due to hesitancy to migrate when the great majority consists of home-stayers compared with a minority of rangers [Reference Broadbridge, Hutchinson, Li and Mann9]. A reaction term then represents the reproduction of the species.
There have been relatively few studies of nonlinear hyperbolic reaction-diffusion equations. In particular, constructions of useful exact solutions are hard to find in the literature. King et al. [Reference King, Needham and Scott27] and Leach and Bassom [Reference Leach and Bassom31]) gave asymptotic properties and exact weak travelling wave solutions for the hyperbolic Fisher equation. Polyanin et al. [Reference Polyanin, Sorokin and Vyazmin37] produced some solutions with free functions when R has a special dependence on both density
![]() $\theta (x,t)$
and past density
$\theta (x,t)$
and past density
![]() $\theta (x,t-\tau )$
with a fixed delay. Lenzi et al. [Reference Lenzi, Lenzi, Zola and Evangelista32] constructed some exact solutions for models with linear source terms.
$\theta (x,t-\tau )$
with a fixed delay. Lenzi et al. [Reference Lenzi, Lenzi, Zola and Evangelista32] constructed some exact solutions for models with linear source terms.
For the parabolic case (
![]() $\tau =0$
), there is a class of function pairs
$\tau =0$
), there is a class of function pairs
![]() $(D(\theta ), R(\theta ))$
that gives rise to a special nonclassical symmetry and exact solutions by functional separation of variables [Reference Goard and Broadbridge23], allowing for Dirichlet, Neumann and Robin boundary conditions [Reference Ern, Guermond, Ern and Guermond17] in terms of the flux potential on compact domains [Reference Broadbridge and Bradshaw-Hajek5]. The question then naturally arises as to whether such a construction still applies in the case
$(D(\theta ), R(\theta ))$
that gives rise to a special nonclassical symmetry and exact solutions by functional separation of variables [Reference Goard and Broadbridge23], allowing for Dirichlet, Neumann and Robin boundary conditions [Reference Ern, Guermond, Ern and Guermond17] in terms of the flux potential on compact domains [Reference Broadbridge and Bradshaw-Hajek5]. The question then naturally arises as to whether such a construction still applies in the case
![]() $\tau>0$
. The answer is indeed in the affirmative. In Section 2, we develop the nonclassical symmetry reduction for conformable function pairs
$\tau>0$
. The answer is indeed in the affirmative. In Section 2, we develop the nonclassical symmetry reduction for conformable function pairs
![]() $(D(\theta ),R(\theta ))$
in which one or both of the functions depend on
$(D(\theta ),R(\theta ))$
in which one or both of the functions depend on
![]() $\tau $
. In those cases, we can construct an exact solution from any solution of the linear Helmholtz equation. This affords an infinite-dimensional class of exact solutions, not simply a two-dimensional class that would result from a sequence of successive classical symmetry reductions. Those special nonlinear hyperbolic reaction-diffusion equations are conditionally integrable.
$\tau $
. In those cases, we can construct an exact solution from any solution of the linear Helmholtz equation. This affords an infinite-dimensional class of exact solutions, not simply a two-dimensional class that would result from a sequence of successive classical symmetry reductions. Those special nonlinear hyperbolic reaction-diffusion equations are conditionally integrable.
In Section 3, we construct exact solutions for a Verhulst–Fisher–KPP class [Reference Kolmogorov, Petrovsky and Piscounov29] of population growth functions with
![]() $R=s\theta +\mathcal O(\theta ^2)$
at small
$R=s\theta +\mathcal O(\theta ^2)$
at small
![]() $\theta $
and
$\theta $
and
![]() $R=0$
at carrying capacity. This includes a solution for a single species within a fisheries no-take area. It is found that the critical domain size of a no-take area depends only on
$R=0$
at carrying capacity. This includes a solution for a single species within a fisheries no-take area. It is found that the critical domain size of a no-take area depends only on
![]() $D(0)$
and s, with no dependence on
$D(0)$
and s, with no dependence on
![]() $\tau $
. In Section 4, we construct exact solutions for a single species with weak Allee effect,
$\tau $
. In Section 4, we construct exact solutions for a single species with weak Allee effect,
![]() $R=s\theta ^2+\mathcal O(\theta ^3)$
at small
$R=s\theta ^2+\mathcal O(\theta ^3)$
at small
![]() $\theta $
, and still with a carrying capacity so that
$\theta $
, and still with a carrying capacity so that
![]() $R=0$
at
$R=0$
at
![]() $\theta =\theta _c>0.$
In Section 5, we find exact solutions for nonlinear heat transport with a reaction term that is exactly the nonanalytic Arrhenius combustion term [Reference Fowler21] for a monomolecular reaction at the leading order of
$\theta =\theta _c>0.$
In Section 5, we find exact solutions for nonlinear heat transport with a reaction term that is exactly the nonanalytic Arrhenius combustion term [Reference Fowler21] for a monomolecular reaction at the leading order of
![]() $\tau $
.
$\tau $
.
2 Nonclassical symmetry reduction of a conditionally integrable PDE
For ease of analysis, we will sometimes use the Kirchhoff flux potential u as the dependent variable [Reference Kirchhoff28]:
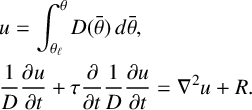 $$ \begin{align}\begin{aligned} &u=\int_{\theta_\ell}^\theta D(\bar\theta)\,d\bar\theta,\\ &\frac{1}{D}\frac{\partial u}{\partial t}+\tau\frac{\partial }{\partial t}\frac{1}{D}\frac{\partial u}{\partial t}=\nabla^2u+R. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &u=\int_{\theta_\ell}^\theta D(\bar\theta)\,d\bar\theta,\\ &\frac{1}{D}\frac{\partial u}{\partial t}+\tau\frac{\partial }{\partial t}\frac{1}{D}\frac{\partial u}{\partial t}=\nabla^2u+R. \end{aligned}\end{align} $$
Here,
![]() $\theta _l$
is some concentration level of significance. For example,
$\theta _l$
is some concentration level of significance. For example,
![]() $\theta _\ell $
is often chosen to be zero, or a zero of the reaction function,
$\theta _\ell $
is often chosen to be zero, or a zero of the reaction function,
![]() $R(\theta _\ell )=0$
which gives a uniform fixed-point solution. Then up to order
$R(\theta _\ell )=0$
which gives a uniform fixed-point solution. Then up to order
![]() $\tau $
, the flux density is
$\tau $
, the flux density is
![]() ${\mathbf J}(x,t)=-\nabla u(x,t-\tau ).$
When
${\mathbf J}(x,t)=-\nabla u(x,t-\tau ).$
When
![]() $\tau =0$
, there are some paired combinations of functions
$\tau =0$
, there are some paired combinations of functions
![]() $(D(\theta ),R(\theta ))$
that result in equation (2.1) admitting the simple nonclassical symmetry
$(D(\theta ),R(\theta ))$
that result in equation (2.1) admitting the simple nonclassical symmetry
This one-parameter transformation is not an invariance transformation for equation (2.1), so it is not a classical symmetry. However, under this transformation, there are invariant solutions of equation (2.1) that are compatible with the invariant surface condition [Reference Arrigo and Beckham4], which in this case is simply the equation
![]() $u_t=Au$
. This is just the condition that there is an invariant solution
$u_t=Au$
. This is just the condition that there is an invariant solution
![]() $u=f(x_j,t)$
satisfying
$u=f(x_j,t)$
satisfying
![]() $(d/d\epsilon )[u'-f(x_j',t')]=0.$
For every Lie symmetry, there is a canonical coordinate system consisting of independent invariants plus a translation variable
$(d/d\epsilon )[u'-f(x_j',t')]=0.$
For every Lie symmetry, there is a canonical coordinate system consisting of independent invariants plus a translation variable
![]() $\xi $
that undergoes simple translation
$\xi $
that undergoes simple translation
![]() $\xi '=\xi +\epsilon $
under the action of the symmetry operation. For example, for rotations by angle
$\xi '=\xi +\epsilon $
under the action of the symmetry operation. For example, for rotations by angle
![]() $\epsilon $
about the origin in the plane, two independent invariants are the dependent variable u and the radial coordinate r. One translation variable is the polar angle
$\epsilon $
about the origin in the plane, two independent invariants are the dependent variable u and the radial coordinate r. One translation variable is the polar angle
![]() $\phi $
. In the current case, we have invariants
$\phi $
. In the current case, we have invariants
![]() $x^j$
and
$x^j$
and
![]() $\Phi =ue^{-At}$
, while t is a translation variable. Then after symmetry reduction, invariant solutions have the form of a functional separation of variables
$\Phi =ue^{-At}$
, while t is a translation variable. Then after symmetry reduction, invariant solutions have the form of a functional separation of variables
![]() $u(\theta )=\Phi ({\mathbf x})e^{At}$
. Note that, in general,
$u(\theta )=\Phi ({\mathbf x})e^{At}$
. Note that, in general,
![]() $\theta $
is a nonlinear function of u, so it is not simply exponential in t. For the relationship between Lie symmetry and separability in many familiar standard PDEs, we refer to [Reference Miller, Levi and Winternitz35].
$\theta $
is a nonlinear function of u, so it is not simply exponential in t. For the relationship between Lie symmetry and separability in many familiar standard PDEs, we refer to [Reference Miller, Levi and Winternitz35].
General noninvariant solutions may be written in the form
![]() $u=\Phi ({\mathbf x},t)e^{At}$
. Before any reduction of variables, this is to be regarded as a change of variables
$u=\Phi ({\mathbf x},t)e^{At}$
. Before any reduction of variables, this is to be regarded as a change of variables
![]() $(x_j,t,u)\to (x_j,t,\Phi )$
. Under that change of variable, the PDE in equation (1.1) is equivalent to
$(x_j,t,u)\to (x_j,t,\Phi )$
. Under that change of variable, the PDE in equation (1.1) is equivalent to
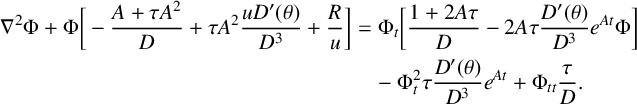 $$ \begin{align} \nabla^2\Phi+\Phi\bigg[-\frac{A+\tau A^2}{D}+\tau A^2\frac{uD'(\theta)}{D^3}+\frac Ru\bigg] &=\Phi_t\bigg[\frac{1+2A\tau}{D}-2A\tau\frac{D'(\theta)}{D^3}e^{At}\Phi\bigg] \nonumber \\ &\quad -\Phi_t^2\tau\frac{D'(\theta)}{D^3}e^{At}+\Phi_{tt}\frac\tau D. \end{align} $$
$$ \begin{align} \nabla^2\Phi+\Phi\bigg[-\frac{A+\tau A^2}{D}+\tau A^2\frac{uD'(\theta)}{D^3}+\frac Ru\bigg] &=\Phi_t\bigg[\frac{1+2A\tau}{D}-2A\tau\frac{D'(\theta)}{D^3}e^{At}\Phi\bigg] \nonumber \\ &\quad -\Phi_t^2\tau\frac{D'(\theta)}{D^3}e^{At}+\Phi_{tt}\frac\tau D. \end{align} $$
The first square bracketed term is autonomous in t when R and D are related by
where
![]() $k^2$
is a real valued function of x, independent of t. Thence, in the consequent form of equation (2.2), we have the general form of a PDE that is consistent with the proposed nonclassical symmetry. Noting that
$k^2$
is a real valued function of x, independent of t. Thence, in the consequent form of equation (2.2), we have the general form of a PDE that is consistent with the proposed nonclassical symmetry. Noting that
![]() $D(\theta )=u'(\theta )$
, if
$D(\theta )=u'(\theta )$
, if
![]() $R(\theta )$
is specified as a function, then equation (2.3) is a second-order nonlinear differential equation for
$R(\theta )$
is specified as a function, then equation (2.3) is a second-order nonlinear differential equation for
![]() $u(\theta )$
. When
$u(\theta )$
. When
![]() $\tau =0$
, it reduces to a first-order differential equation that is also separable when
$\tau =0$
, it reduces to a first-order differential equation that is also separable when
![]() $k=0$
. If the flux potential
$k=0$
. If the flux potential
![]() $u(\theta )$
is specified as a function, then each of the modelling functions
$u(\theta )$
is specified as a function, then each of the modelling functions
![]() $D(\theta )$
and
$D(\theta )$
and
![]() $R(\theta )$
follows directly from
$R(\theta )$
follows directly from
![]() $u(\theta )$
by differentiation
$u(\theta )$
by differentiation
![]() $D(\theta )=u'(\theta )$
and by explicit algebraic construction in equation (2.3).
$D(\theta )=u'(\theta )$
and by explicit algebraic construction in equation (2.3).
When
![]() $\Phi _t({\mathbf x},t)$
is identically zero, the reduced equation for
$\Phi _t({\mathbf x},t)$
is identically zero, the reduced equation for
![]() $\Phi ({\mathbf x})$
has no coefficients that depend on t. Then there is a consistent reduction of variables. For the remainder of this article, we assume that
$\Phi ({\mathbf x})$
has no coefficients that depend on t. Then there is a consistent reduction of variables. For the remainder of this article, we assume that
![]() $k^2$
is simply constant. Then the reduced equation is simply the linear Helmholtz equation
$k^2$
is simply constant. Then the reduced equation is simply the linear Helmholtz equation
From every member of the infinite dimensional solution space of the Helmholtz equation, a solution can be constructed for the nonlinear hyperbolic reaction diffusion equation (1.1) that has the structure of equation (2.3). However, this does not give all the solutions of equation (1.1), only those satisfying the side condition
![]() $u_t=Au$
with
$u_t=Au$
with
![]() $du/d\theta =D(\theta )$
. In that sense, the nonlinear PDE is conditionally integrable. This is to be compared with a classical Lie symmetry, in which case equation (2.2) would immediately be autonomous in t. That is to say, the equation itself, and not just a particular subclass of solutions, would be invariant. Generally speaking, reduction of a PDE by successive classical Lie symmetries leads to an ordinary differential equation and a finite- rather than infinite-dimensional manifold of solutions.
$du/d\theta =D(\theta )$
. In that sense, the nonlinear PDE is conditionally integrable. This is to be compared with a classical Lie symmetry, in which case equation (2.2) would immediately be autonomous in t. That is to say, the equation itself, and not just a particular subclass of solutions, would be invariant. Generally speaking, reduction of a PDE by successive classical Lie symmetries leads to an ordinary differential equation and a finite- rather than infinite-dimensional manifold of solutions.
3 Reaction term of Fisher–KPP type
For a model of Fisher–KPP type [Reference Fisher20, Reference Kolmogorov, Petrovsky and Piscounov29], the target reaction function is considered to be the canonical Verhulst form
![]() $R(\theta )=s\theta (1-\theta )$
, where the density is dimensionless, having been scaled by the carrying capacity. To approximate the structure of a target reaction function
$R(\theta )=s\theta (1-\theta )$
, where the density is dimensionless, having been scaled by the carrying capacity. To approximate the structure of a target reaction function
![]() $R(\theta )$
, it is convenient to express equation (2.3) as
$R(\theta )$
, it is convenient to express equation (2.3) as
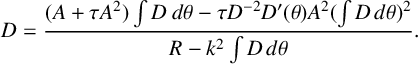 $$ \begin{align} D=\frac{(A+\tau A^2)\int D~d\theta-\tau D^{-2}D'(\theta)A^2(\int D\,d\theta)^2}{R-k^2\int D\,d\theta}. \end{align} $$
$$ \begin{align} D=\frac{(A+\tau A^2)\int D~d\theta-\tau D^{-2}D'(\theta)A^2(\int D\,d\theta)^2}{R-k^2\int D\,d\theta}. \end{align} $$
Consider a model of Fisher–KPP type
![]() $R=s\theta -s\theta ^2+\mathcal O(\theta ^3);~ D=D_0+\mathcal O(\theta )$
near
$R=s\theta -s\theta ^2+\mathcal O(\theta ^3);~ D=D_0+\mathcal O(\theta )$
near
![]() $\theta =0$
with
$\theta =0$
with
![]() $D_0>0$
and
$D_0>0$
and
![]() $s>0$
. Then equation (3.1) implies
$s>0$
. Then equation (3.1) implies
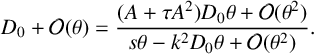 $$ \begin{align*}D_0+\mathcal O(\theta)=\frac{(A+\tau A^2)D_0\theta +\mathcal O(\theta^2)}{s\theta-k^2D_0\theta+\mathcal O(\theta^2)}.\end{align*} $$
$$ \begin{align*}D_0+\mathcal O(\theta)=\frac{(A+\tau A^2)D_0\theta +\mathcal O(\theta^2)}{s\theta-k^2D_0\theta+\mathcal O(\theta^2)}.\end{align*} $$
Taking the limit
![]() $\theta \to 0$
in equation (3.1) gives
$\theta \to 0$
in equation (3.1) gives
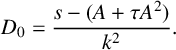 $$ \begin{align} D_0=\frac{s-(A+\tau A^2)}{k^2}. \end{align} $$
$$ \begin{align} D_0=\frac{s-(A+\tau A^2)}{k^2}. \end{align} $$
Choose
![]() $D_0(\theta )=D(0)$
(constant). Then apply equation (3.1) as a recurrence relation
$D_0(\theta )=D(0)$
(constant). Then apply equation (3.1) as a recurrence relation
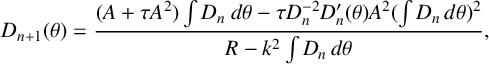 $$ \begin{align*} D_{n+1}(\theta)=\frac{(A+\tau A^2)\int D_n~d\theta-\tau D_n^{-2}D_n'(\theta)A^2(\int D_n\,d\theta)^2}{R-k^2\int D_n\,d\theta}, \end{align*} $$
$$ \begin{align*} D_{n+1}(\theta)=\frac{(A+\tau A^2)\int D_n~d\theta-\tau D_n^{-2}D_n'(\theta)A^2(\int D_n\,d\theta)^2}{R-k^2\int D_n\,d\theta}, \end{align*} $$
where R is kept at the target
![]() $R(\theta )=s\theta (1-\theta ).$
For some cases of the parabolic (
$R(\theta )=s\theta (1-\theta ).$
For some cases of the parabolic (
![]() $\tau =0$
) model with R bounded, such as in the Arrhenius reaction term, this gives a contraction map on
$\tau =0$
) model with R bounded, such as in the Arrhenius reaction term, this gives a contraction map on
![]() $L^\infty $
that converges to the partner
$L^\infty $
that converges to the partner
![]() $D(\theta )$
that solves equation (3.1). It is not known if this can be a contraction map when
$D(\theta )$
that solves equation (3.1). It is not known if this can be a contraction map when
![]() $\tau>0$
. In any case, the first iteration gives a useful function
$\tau>0$
. In any case, the first iteration gives a useful function
![]() $D_1$
from which a useful partner reaction term
$D_1$
from which a useful partner reaction term
![]() $R_1(\theta )$
can be constructed explicitly from equation (3.1) by integration:
$R_1(\theta )$
can be constructed explicitly from equation (3.1) by integration:
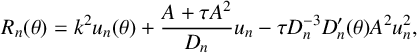 $$ \begin{align*} R_n(\theta)=k^2u_n(\theta)+\frac{A+\tau A^2}{D_n}u_n-\tau D_n^{-3}D_n'(\theta)A^2 u_n^2, \end{align*} $$
$$ \begin{align*} R_n(\theta)=k^2u_n(\theta)+\frac{A+\tau A^2}{D_n}u_n-\tau D_n^{-3}D_n'(\theta)A^2 u_n^2, \end{align*} $$
where
![]() $u_n(\theta )=\int _{\theta _\ell }^\theta D_n(\bar \theta )\,d\bar \theta $
. However,
$u_n(\theta )=\int _{\theta _\ell }^\theta D_n(\bar \theta )\,d\bar \theta $
. However,
![]() $\theta _\ell $
is chosen to be zero so that
$\theta _\ell $
is chosen to be zero so that
![]() $R\to 0$
as
$R\to 0$
as
![]() $\theta \to 0$
, the necessity of which is shown in the sequel. The construction of Broadbridge and Bradshaw-Hajek [Reference Broadbridge and Bradshaw-Hajek5] for
$\theta \to 0$
, the necessity of which is shown in the sequel. The construction of Broadbridge and Bradshaw-Hajek [Reference Broadbridge and Bradshaw-Hajek5] for
![]() $\tau>0$
now extends to
$\tau>0$
now extends to
![]() $\tau \ge 0$
:
$\tau \ge 0$
:
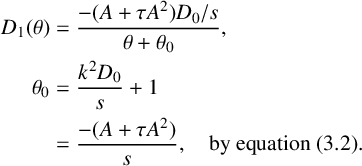 $$ \begin{align*} D_1(\theta)&=\frac{-(A+\tau A^2)D_0/s}{\theta+\theta_0}, \\ \theta_0&=\frac {k^2D_0}{s}+1\\ &=\frac{-(A+\tau A^2)}{s}, \quad \mbox{by equation}\ (3.2). \end{align*} $$
$$ \begin{align*} D_1(\theta)&=\frac{-(A+\tau A^2)D_0/s}{\theta+\theta_0}, \\ \theta_0&=\frac {k^2D_0}{s}+1\\ &=\frac{-(A+\tau A^2)}{s}, \quad \mbox{by equation}\ (3.2). \end{align*} $$
Assume
![]() $A<0$
. Then,
$A<0$
. Then,
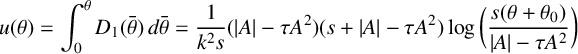 $$ \begin{align*} u(\theta)=\int _0^\theta D_1(\bar\theta)\,d\bar\theta=\frac{1}{k^2s}(|A|-\tau A^2)(s+|A|-\tau A^2)\log \bigg( \frac{s(\theta+\theta_0)}{|A|-\tau A^2}\bigg) \end{align*} $$
$$ \begin{align*} u(\theta)=\int _0^\theta D_1(\bar\theta)\,d\bar\theta=\frac{1}{k^2s}(|A|-\tau A^2)(s+|A|-\tau A^2)\log \bigg( \frac{s(\theta+\theta_0)}{|A|-\tau A^2}\bigg) \end{align*} $$
and
 $$ \begin{align*} R_1&=\log\bigg(1+\frac{\theta }{\theta_0}\bigg)\bigg[\bigg(\frac{(s+|A|-\tau A^2)}{ s}\bigg)(|A|-\tau A^2)-(|A|-\tau A^2)(\theta+\theta_0)\bigg]\\ &\quad +\tau A^2(\theta+\theta_0)\bigg[\log\bigg(1+\frac{\theta }{\theta_0}\bigg)\bigg]^2=s\theta+\mathcal O(\theta^2). \end{align*} $$
$$ \begin{align*} R_1&=\log\bigg(1+\frac{\theta }{\theta_0}\bigg)\bigg[\bigg(\frac{(s+|A|-\tau A^2)}{ s}\bigg)(|A|-\tau A^2)-(|A|-\tau A^2)(\theta+\theta_0)\bigg]\\ &\quad +\tau A^2(\theta+\theta_0)\bigg[\log\bigg(1+\frac{\theta }{\theta_0}\bigg)\bigg]^2=s\theta+\mathcal O(\theta^2). \end{align*} $$
Note that
![]() $R_1(\theta )$
has zeros at
$R_1(\theta )$
has zeros at
![]() $\theta =0$
and where
$\theta =0$
and where
![]() $\theta =\bar \theta _c$
such that
$\theta =\bar \theta _c$
such that
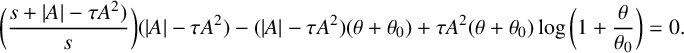 $$ \begin{align*}\bigg(\frac{s+|A|-\tau A^2)}{ s}\bigg)(|A|-\tau A^2)-(|A|-\tau A^2)(\theta+\theta_0)+\tau A^2(\theta+\theta_0)\log\bigg(1+\frac{\theta }{\theta_0}\bigg)=0.\end{align*} $$
$$ \begin{align*}\bigg(\frac{s+|A|-\tau A^2)}{ s}\bigg)(|A|-\tau A^2)-(|A|-\tau A^2)(\theta+\theta_0)+\tau A^2(\theta+\theta_0)\log\bigg(1+\frac{\theta }{\theta_0}\bigg)=0.\end{align*} $$
This transcendental equation can be expressed in normal form as
where
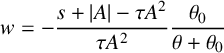 $$ \begin{align*} w=-\frac{s+|A|-\tau A^2}{\tau A^2}\frac{\theta_0}{\theta+\theta_0} \end{align*} $$
$$ \begin{align*} w=-\frac{s+|A|-\tau A^2}{\tau A^2}\frac{\theta_0}{\theta+\theta_0} \end{align*} $$
and
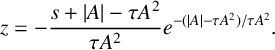 $$ \begin{align*} z=-\frac{s+|A|-\tau A^2}{\tau A^2}e^{-(|A|-\tau A^2)/\tau A^2}. \end{align*} $$
$$ \begin{align*} z=-\frac{s+|A|-\tau A^2}{\tau A^2}e^{-(|A|-\tau A^2)/\tau A^2}. \end{align*} $$
Note that as
![]() $\tau \to 0$
,
$\tau \to 0$
,
![]() $\theta _0\to |A|/s, \bar \theta _c\to 1, z\to 0$
and
$\theta _0\to |A|/s, \bar \theta _c\to 1, z\to 0$
and
![]() $w\to -\infty $
. Therefore, the solution is
$w\to -\infty $
. Therefore, the solution is
where
![]() $W_{-1}$
is the real negative branch of the Lambert W function [Reference Corless, Gonnet, Hare, Jeffrey and Knuth14]. Then,
$W_{-1}$
is the real negative branch of the Lambert W function [Reference Corless, Gonnet, Hare, Jeffrey and Knuth14]. Then,
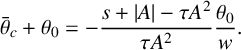 $$ \begin{align*} \bar\theta_c+\theta_0=-\frac{s+|A|-\tau A^2}{\tau A^2}\frac{\theta_0}{w}. \end{align*} $$
$$ \begin{align*} \bar\theta_c+\theta_0=-\frac{s+|A|-\tau A^2}{\tau A^2}\frac{\theta_0}{w}. \end{align*} $$
When
![]() $\tau> 0$
, the positive root
$\tau> 0$
, the positive root
![]() $\bar \theta _c$
of
$\bar \theta _c$
of
![]() $R_1$
is now larger than 1. However, we can rescale the dependent variable to
$R_1$
is now larger than 1. However, we can rescale the dependent variable to
![]() $\Theta =\theta /\bar \theta _c$
to achieve a reaction diffusion equation with zero reaction at
$\Theta =\theta /\bar \theta _c$
to achieve a reaction diffusion equation with zero reaction at
![]() $\Theta =1$
,
$\Theta =1$
,
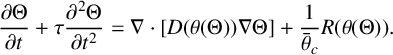 $$ \begin{align*} \frac{\partial \Theta}{\partial t}+\tau \frac{\partial^2 \Theta}{\partial t^2}=\nabla\cdot[D(\theta(\Theta))\nabla\Theta]+\frac{1}{\bar\theta_c}R(\theta(\Theta)). \end{align*} $$
$$ \begin{align*} \frac{\partial \Theta}{\partial t}+\tau \frac{\partial^2 \Theta}{\partial t^2}=\nabla\cdot[D(\theta(\Theta))\nabla\Theta]+\frac{1}{\bar\theta_c}R(\theta(\Theta)). \end{align*} $$
Note that after rescaling
![]() $\theta $
, the governing equation still takes the form of equation (1.1) and the nonlinear coefficient functions still obey a relationship of the form in equation (2.3).
$\theta $
, the governing equation still takes the form of equation (1.1) and the nonlinear coefficient functions still obey a relationship of the form in equation (2.3).
A zero population boundary condition represents lethal over-harvesting in the exterior of a protected reserve. With zero population at a circular boundary
![]() $r=a$
, there is a solution of the form
$r=a$
, there is a solution of the form
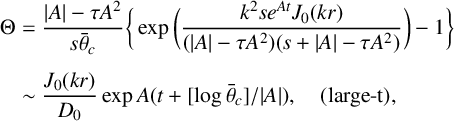 $$ \begin{align*} \Theta&=\frac{|A|-\tau A^2}{s\bar\theta_c}\bigg\{\exp \bigg (\frac{k^2se^{At}J_0(kr)}{(|A|-\tau A^2)(s+|A|-\tau A^2)}\bigg )-1\bigg\}\\[5pt] &\sim \frac{J_0(kr)}{D_0}\exp A(t+[\log\bar\theta_c]/|A|),\quad \mbox{(large-t)}, \end{align*} $$
$$ \begin{align*} \Theta&=\frac{|A|-\tau A^2}{s\bar\theta_c}\bigg\{\exp \bigg (\frac{k^2se^{At}J_0(kr)}{(|A|-\tau A^2)(s+|A|-\tau A^2)}\bigg )-1\bigg\}\\[5pt] &\sim \frac{J_0(kr)}{D_0}\exp A(t+[\log\bar\theta_c]/|A|),\quad \mbox{(large-t)}, \end{align*} $$
where
![]() $k=\lambda _{0,1}/a$
,
$k=\lambda _{0,1}/a$
,
![]() $\lambda _{0,1}\approx 2.404$
(first zero of Bessel
$\lambda _{0,1}\approx 2.404$
(first zero of Bessel
![]() $J_0$
[Reference Skellam39]). For specified linear homogeneous boundary conditions for
$J_0$
[Reference Skellam39]). For specified linear homogeneous boundary conditions for
![]() $u(x,t)$
on a compact connected domain, k is of the form
$u(x,t)$
on a compact connected domain, k is of the form
![]() $\lambda /a$
, where the geometric length scale a and the dimensionless factor
$\lambda /a$
, where the geometric length scale a and the dimensionless factor
![]() $\lambda $
depend on the geometry of the domain. For a line segment of length a,
$\lambda $
depend on the geometry of the domain. For a line segment of length a,
![]() $k=\pi /a$
. For a rectangle,
$k=\pi /a$
. For a rectangle,
![]() $\lambda =\pi $
and a is the hyperbolic root mean square length of sides [Reference Broadbridge and Hutchinson8]. Now consider the Fisher–KPP class with
$\lambda =\pi $
and a is the hyperbolic root mean square length of sides [Reference Broadbridge and Hutchinson8]. Now consider the Fisher–KPP class with
![]() $R=s\theta + \mathcal O(\theta ^2).$
The fundamental relationship in equation (3.2) implies
$R=s\theta + \mathcal O(\theta ^2).$
The fundamental relationship in equation (3.2) implies
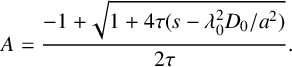 $$ \begin{align} A=\frac{-1+\sqrt{1+4\tau(s-\lambda_0^2D_0/a^2)}}{2\tau}. \end{align} $$
$$ \begin{align} A=\frac{-1+\sqrt{1+4\tau(s-\lambda_0^2D_0/a^2)}}{2\tau}. \end{align} $$
In applications such as no-take areas for conservation within fisheries, it is important that the extinction point
![]() $\theta =0$
be unstable. Then it is necessary that
$\theta =0$
be unstable. Then it is necessary that
![]() $A>0$
which, by equation (3.3), is equivalent to
$A>0$
which, by equation (3.3), is equivalent to
Importantly, this is independent of the delay
![]() $\tau $
. In the case
$\tau $
. In the case
![]() $\tau =0$
, this is the well-known criterion for instability of the extinction point, originally obtained by linear stability theory [Reference Skellam39].
$\tau =0$
, this is the well-known criterion for instability of the extinction point, originally obtained by linear stability theory [Reference Skellam39].
Figure 1 Solvable model of Fisher–KPP type. Parameters used:
![]() $A=-1.5, s=1, k=2.4048$
.
$A=-1.5, s=1, k=2.4048$
.
For the example with
![]() $\tau =0.1, s=1, ~A=-1.5$
, in Figure 1, the partner diffusivity and reaction functions are plotted as functions of the scaled population density. Note that by equation (3.2), D must decrease with
$\tau =0.1, s=1, ~A=-1.5$
, in Figure 1, the partner diffusivity and reaction functions are plotted as functions of the scaled population density. Note that by equation (3.2), D must decrease with
![]() $\tau $
whenever
$\tau $
whenever
![]() $A\ne 0$
. With larger delay
$A\ne 0$
. With larger delay
![]() $\tau $
, diffusivity is lower to achieve the same nonzero decay rate
$\tau $
, diffusivity is lower to achieve the same nonzero decay rate
![]() $-A$
. Conversely, if both
$-A$
. Conversely, if both
![]() $D_0$
and s were prescribed, decay would be more rapid in the case of larger
$D_0$
and s were prescribed, decay would be more rapid in the case of larger
![]() $\tau $
. In fact, in the first application of the telegraph equation by Heaviside,
$\tau $
. In fact, in the first application of the telegraph equation by Heaviside,
![]() $\tau $
was proportional to the electrical resistance of the medium.
$\tau $
was proportional to the electrical resistance of the medium.
4 Reaction term of Huxley form with weak Allee effect
The simplest form of an equation with weak Allee effect [Reference Allee and Bowen3] is the Huxley equation (see [Reference Chin12] and the references therein), which has
Again, it is assumed here that the density has been scaled by the carrying capacity so that it is dimensionless. In fact, this reaction term arises as the growth of a density of a new favourable allele under Mendelian inheritance [Reference Russell38], not the Fisher equation as is frequently supposed (for example, see [Reference Broadbridge, Bradshaw, Fulford and Aldis6]). As a model of population growth, at low population, it has the per-capita growth rate
![]() $R/\theta \approx s\theta -s\theta ^2$
increasing from zero, rather than being a positive constant or decreasing from a positive constant, as in the Malthusian and Verhulst models [Reference Iannelli and Pugliese26]. Since the growth rate is not negative near
$R/\theta \approx s\theta -s\theta ^2$
increasing from zero, rather than being a positive constant or decreasing from a positive constant, as in the Malthusian and Verhulst models [Reference Iannelli and Pugliese26]. Since the growth rate is not negative near
![]() $\theta =0$
, this is a weak Allee effect rather than a strong Allee effect (see for example, Courchamp et al. [Reference Courchamp, Berec and Gascoigne15]). Consider
$\theta =0$
, this is a weak Allee effect rather than a strong Allee effect (see for example, Courchamp et al. [Reference Courchamp, Berec and Gascoigne15]). Consider
![]() $R=s\theta ^2+\mathcal O(\theta ^3)$
and
$R=s\theta ^2+\mathcal O(\theta ^3)$
and
![]() $D=D_0+\mathcal O(\theta )$
near
$D=D_0+\mathcal O(\theta )$
near
![]() $\theta =0$
with
$\theta =0$
with
![]() $D_0>0$
and
$D_0>0$
and
![]() $s>0$
. Then equation (3.1) implies
$s>0$
. Then equation (3.1) implies
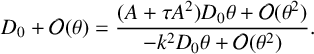 $$ \begin{align*} D_0+\mathcal O(\theta)=\frac{(A+\tau A^2)D_0\theta +\mathcal O(\theta^2)}{-k^2D_0\theta+\mathcal O(\theta^2)}. \end{align*} $$
$$ \begin{align*} D_0+\mathcal O(\theta)=\frac{(A+\tau A^2)D_0\theta +\mathcal O(\theta^2)}{-k^2D_0\theta+\mathcal O(\theta^2)}. \end{align*} $$
Taking the limit
![]() $\theta \to 0$
in equation (3.1) gives the result
$\theta \to 0$
in equation (3.1) gives the result
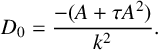 $$ \begin{align*} D_0=\frac{-(A+\tau A^2)}{k^2}. \end{align*} $$
$$ \begin{align*} D_0=\frac{-(A+\tau A^2)}{k^2}. \end{align*} $$
Then,
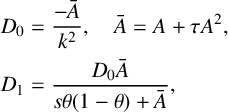 $$ \begin{align*} D_0&=\frac{-\bar A}{k^2}, \quad \bar A=A+\tau A^2, \\[1pt] D_1&=\frac{D_0\bar A}{s\theta(1-\theta)+\bar A}, \end{align*} $$
$$ \begin{align*} D_0&=\frac{-\bar A}{k^2}, \quad \bar A=A+\tau A^2, \\[1pt] D_1&=\frac{D_0\bar A}{s\theta(1-\theta)+\bar A}, \end{align*} $$
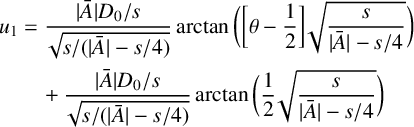 $$ \begin{align} u_1&=\frac{|\bar A|D_0/s}{\sqrt{s/(|\bar A|-s/4)}}\arctan \bigg(\bigg[\theta-\frac 12\bigg] \sqrt{\frac{s}{|\bar A|-s/4}}\bigg) \\[1pt] &\quad +\frac{|\bar A|D_0/s}{\sqrt{s/(|\bar A|-s/4)}}\arctan \bigg(\frac 12\sqrt{\frac{s}{|\bar A|-s/4}}\bigg)\nonumber \end{align} $$
$$ \begin{align} u_1&=\frac{|\bar A|D_0/s}{\sqrt{s/(|\bar A|-s/4)}}\arctan \bigg(\bigg[\theta-\frac 12\bigg] \sqrt{\frac{s}{|\bar A|-s/4}}\bigg) \\[1pt] &\quad +\frac{|\bar A|D_0/s}{\sqrt{s/(|\bar A|-s/4)}}\arctan \bigg(\frac 12\sqrt{\frac{s}{|\bar A|-s/4}}\bigg)\nonumber \end{align} $$
and
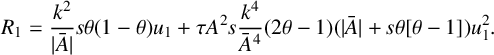 $$ \begin{align*} R_1=\frac{k^2}{|\bar A|}s\theta(1-\theta)u_1+\tau A^2 s\frac{k^4}{\bar A^4}(2\theta-1)(|\bar A|+s\theta[\theta-1])u_1^2. \end{align*} $$
$$ \begin{align*} R_1=\frac{k^2}{|\bar A|}s\theta(1-\theta)u_1+\tau A^2 s\frac{k^4}{\bar A^4}(2\theta-1)(|\bar A|+s\theta[\theta-1])u_1^2. \end{align*} $$
From equation (4.1),
![]() $\theta \to \infty $
as
$\theta \to \infty $
as
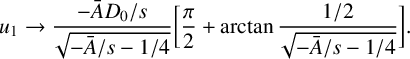 $$ \begin{align*}u_1\to\frac{-\bar AD_0/s}{\sqrt{-\bar A/s- 1/4}}\bigg[\frac\pi 2+\arctan \frac{1/2}{\sqrt{-\bar A/s- 1/4}}\bigg].\end{align*} $$
$$ \begin{align*}u_1\to\frac{-\bar AD_0/s}{\sqrt{-\bar A/s- 1/4}}\bigg[\frac\pi 2+\arctan \frac{1/2}{\sqrt{-\bar A/s- 1/4}}\bigg].\end{align*} $$
Therefore, the maximum value of
![]() $u_1$
must be chosen to be much less than that limiting value. Again, when
$u_1$
must be chosen to be much less than that limiting value. Again, when
![]() $\tau>0$
, the positive zero
$\tau>0$
, the positive zero
![]() $\bar \theta _c$
of
$\bar \theta _c$
of
![]() $R_1$
exceeds 1. After rescaling by
$R_1$
exceeds 1. After rescaling by
![]() ${\Theta =\theta /\bar \theta _c}$
, the compatible diffusivity function and reaction function are plotted in Figure 2.
${\Theta =\theta /\bar \theta _c}$
, the compatible diffusivity function and reaction function are plotted in Figure 2.
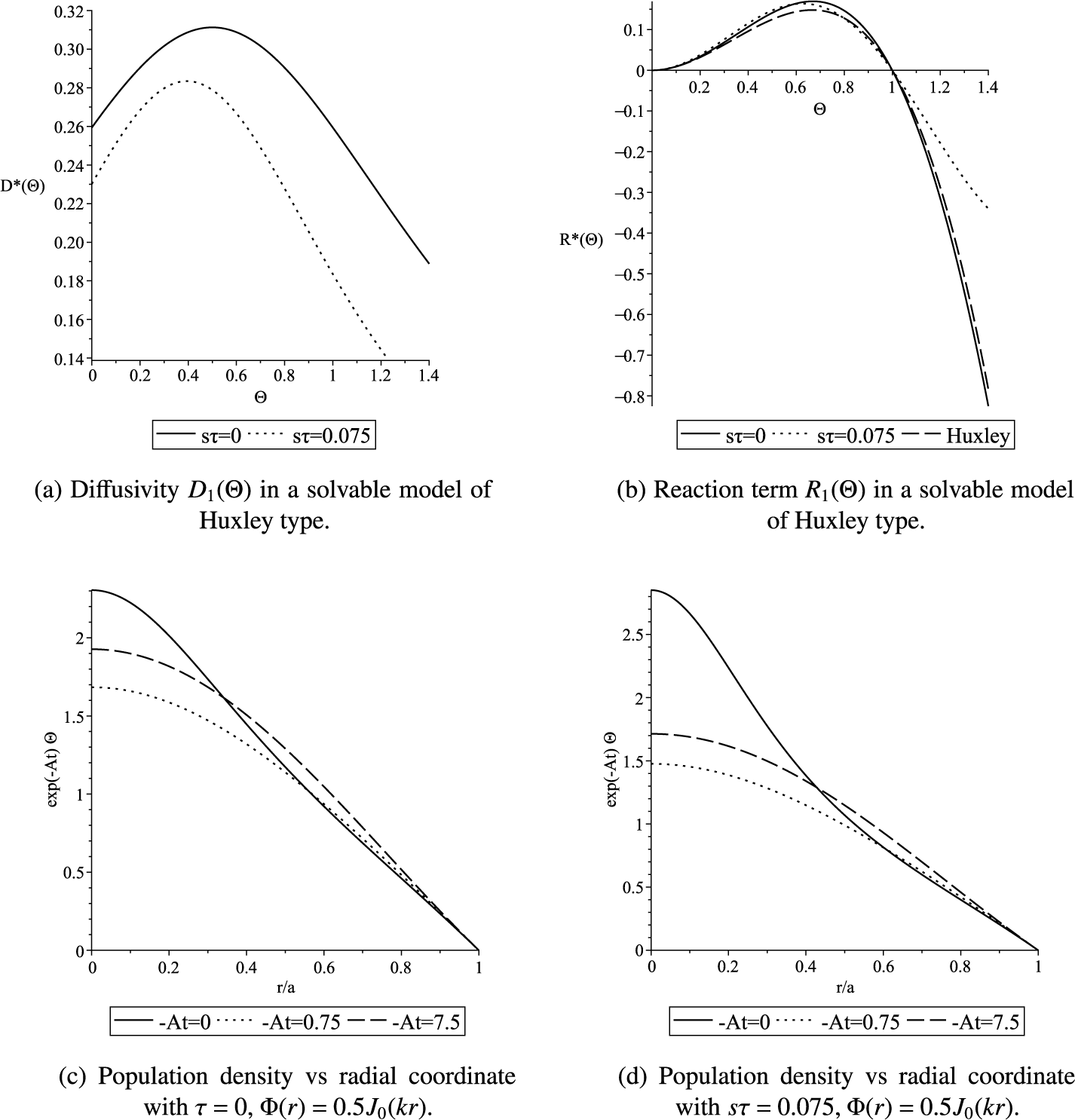
Figure 2 Solvable model of Huxley type. Parameters used:
![]() $A=-1.5, s=1, k=2.4048$
.
$A=-1.5, s=1, k=2.4048$
.
As expected, again with larger delay
![]() $\tau $
, diffusivity is lower to achieve the same logarithmic decay rate
$\tau $
, diffusivity is lower to achieve the same logarithmic decay rate
![]() $-A$
. Conversely, if both
$-A$
. Conversely, if both
![]() $D_0$
and s were prescribed, decay would be more rapid in the case of larger
$D_0$
and s were prescribed, decay would be more rapid in the case of larger
![]() $\tau $
.
$\tau $
.
5 Arrhenius combustion
With
![]() $\theta $
being the absolute temperature, a heat source is of the form
$\theta $
being the absolute temperature, a heat source is of the form
![]() $\rho C R$
, where
$\rho C R$
, where
![]() $\rho $
is density of the medium, C is heat capacity and the rate of temperature increase due to combustion is
$\rho $
is density of the medium, C is heat capacity and the rate of temperature increase due to combustion is
From the Gibbs canonical distribution [Reference Gibbs22], typically
![]() $B=\Delta E/k_B$
, where
$B=\Delta E/k_B$
, where
![]() $\Delta E$
is a molecular activation energy and
$\Delta E$
is a molecular activation energy and
![]() $k_B$
is Boltzmann’s constant. This reaction function is difficult to handle analytically. It is not an analytic function; all derivatives
$k_B$
is Boltzmann’s constant. This reaction function is difficult to handle analytically. It is not an analytic function; all derivatives
![]() $d^nR_0/d\theta ^n$
approach 0 as
$d^nR_0/d\theta ^n$
approach 0 as
![]() $\theta \to 0$
. In the case
$\theta \to 0$
. In the case
![]() $\tau =0$
, the only known exact solution for temperature is that given by Broadbridge et al. [Reference Broadbridge, Bradshaw-Hajek and Triadis7]. The solution requires
$\tau =0$
, the only known exact solution for temperature is that given by Broadbridge et al. [Reference Broadbridge, Bradshaw-Hajek and Triadis7]. The solution requires
![]() $k=0$
and
$k=0$
and
![]() $A>0$
; consequently, the solution is unbounded in both time and space. Given the Arrhenius reaction term, the appropriate solution of equation (2.3) was found to be [Reference Broadbridge, Bradshaw-Hajek and Triadis7]
$A>0$
; consequently, the solution is unbounded in both time and space. Given the Arrhenius reaction term, the appropriate solution of equation (2.3) was found to be [Reference Broadbridge, Bradshaw-Hajek and Triadis7]
where the function
![]() $E_i$
is the exponential integral and
$E_i$
is the exponential integral and
![]() $c_1$
is an arbitrary positive constant with units K m2 s
$c_1$
is an arbitrary positive constant with units K m2 s
![]() $^{-2}$
. Since
$^{-2}$
. Since
![]() $D(\theta)=u'(\theta)$
,
$D(\theta)=u'(\theta)$
,
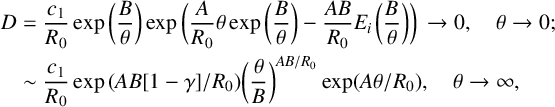 $$ \begin{align*} D&=\frac{c_1}{R_0}\exp\bigg(\frac B\theta\bigg)\exp\bigg(\frac {A}{R_0}\theta\exp\bigg(\frac B\theta\bigg)-\frac{AB}{R_0}E_i\kern1.2pt\bigg(\frac B\theta\bigg)\bigg) \, \to 0, \quad \theta\to 0;\\ &\sim \frac{c_1}{R_0}\exp{(AB[1-\gamma]/R_0)}\bigg(\frac\theta B\bigg)^{AB/R_0}\exp(A\theta/ R_0), \quad \theta\to\infty, \end{align*} $$
$$ \begin{align*} D&=\frac{c_1}{R_0}\exp\bigg(\frac B\theta\bigg)\exp\bigg(\frac {A}{R_0}\theta\exp\bigg(\frac B\theta\bigg)-\frac{AB}{R_0}E_i\kern1.2pt\bigg(\frac B\theta\bigg)\bigg) \, \to 0, \quad \theta\to 0;\\ &\sim \frac{c_1}{R_0}\exp{(AB[1-\gamma]/R_0)}\bigg(\frac\theta B\bigg)^{AB/R_0}\exp(A\theta/ R_0), \quad \theta\to\infty, \end{align*} $$
where
![]() $\gamma =0.5772\ldots $
is Euler’s number. More generally, with
$\gamma =0.5772\ldots $
is Euler’s number. More generally, with
![]() $\tau \ge 0$
, this diffusivity function has a partner reaction function
$\tau \ge 0$
, this diffusivity function has a partner reaction function
This reaction function agrees asymptotically with the Arrhenius reaction as
![]() $\theta \to 0$
and as
$\theta \to 0$
and as
![]() $\theta \to \infty .$
From the form of the reaction and diffusivity functions, there are intrinsic temperature, time and length scales, namely,
$\theta \to \infty .$
From the form of the reaction and diffusivity functions, there are intrinsic temperature, time and length scales, namely,
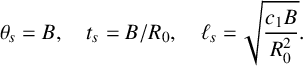 $$ \begin{align*} \theta_s=B, \quad t_s=B/R_0, \quad \ell_s=\sqrt{\frac{c_1B}{R_0^2}}. \end{align*} $$
$$ \begin{align*} \theta_s=B, \quad t_s=B/R_0, \quad \ell_s=\sqrt{\frac{c_1B}{R_0^2}}. \end{align*} $$
In terms of the dimensionless variables
![]() $\vartheta =\theta /\theta _s$
,
$\vartheta =\theta /\theta _s$
,
![]() $t^*=t/t_s$
and
$t^*=t/t_s$
and
![]() $r^*=r/\ell _s$
, equation (1.1) is normalised to
$r^*=r/\ell _s$
, equation (1.1) is normalised to
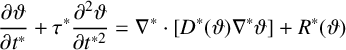 $$ \begin{align*} \frac{\partial \vartheta}{\partial t^*}+\tau^* \frac{\partial^2 \vartheta}{\partial t^{*2}}=\nabla^*\cdot[D^*(\vartheta)\nabla^*\vartheta]+R^*(\vartheta) \end{align*} $$
$$ \begin{align*} \frac{\partial \vartheta}{\partial t^*}+\tau^* \frac{\partial^2 \vartheta}{\partial t^{*2}}=\nabla^*\cdot[D^*(\vartheta)\nabla^*\vartheta]+R^*(\vartheta) \end{align*} $$
with
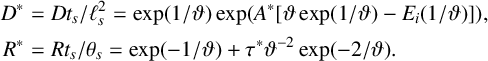 $$ \begin{align*} D^*&=Dt_s/\ell_s^2=\exp(1/\vartheta)\exp(A^*[\vartheta \exp(1/\vartheta)-E_i(1/\vartheta)]), \\ R^*&=Rt_s/\theta_s=\exp(-1/\vartheta)+\tau^*\vartheta^{-2}\exp(-2/\vartheta). \end{align*} $$
$$ \begin{align*} D^*&=Dt_s/\ell_s^2=\exp(1/\vartheta)\exp(A^*[\vartheta \exp(1/\vartheta)-E_i(1/\vartheta)]), \\ R^*&=Rt_s/\theta_s=\exp(-1/\vartheta)+\tau^*\vartheta^{-2}\exp(-2/\vartheta). \end{align*} $$
The dimensionless time lag parameter is
![]() $\tau ^*=R_0\tau /B$
. The other dimensionless parameter is
$\tau ^*=R_0\tau /B$
. The other dimensionless parameter is
![]() $A^*=AB/R_0$
. This is related to the diffusivity at activation temperature by
$A^*=AB/R_0$
. This is related to the diffusivity at activation temperature by
The ratio of the additional reaction component to the Arrhenius reaction is
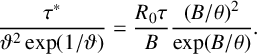 $$ \begin{align*} \frac{\tau^*}{\vartheta^2\exp(1/\vartheta)} =\frac{R_0\tau}{B}\frac{(B/\theta)^2}{\exp(B/\theta)}. \end{align*} $$
$$ \begin{align*} \frac{\tau^*}{\vartheta^2\exp(1/\vartheta)} =\frac{R_0\tau}{B}\frac{(B/\theta)^2}{\exp(B/\theta)}. \end{align*} $$
This approaches 0 at very small and very large
![]() $\theta $
, and it attains the maximum value
$\theta $
, and it attains the maximum value
![]() $4R_0\tau /e^2B$
at
$4R_0\tau /e^2B$
at
![]() $\theta =0.5 B$
. This is a small fraction, equivalent to the ratio of the heat released over one collision time to the total heat content of the material at activation temperature. As an example, with
$\theta =0.5 B$
. This is a small fraction, equivalent to the ratio of the heat released over one collision time to the total heat content of the material at activation temperature. As an example, with
![]() $k=0$
, there is an elementary radial solution
$k=0$
, there is an elementary radial solution
![]() $u/u_0=\log (r/a)$
(
$u/u_0=\log (r/a)$
(
![]() $u_0$
constant) to the exterior problem with boundary condition
$u_0$
constant) to the exterior problem with boundary condition
![]() $\theta (a,t)=0$
. The isotherms follow exactly from the mapping
$\theta (a,t)=0$
. The isotherms follow exactly from the mapping
The radial solution is plotted in Figure 3. At the circle
![]() $r=a_1>a$
, the radial heat flux density
$r=a_1>a$
, the radial heat flux density
![]() $j(r)$
, which is
$j(r)$
, which is
![]() $-u'(r)$
, satisfies
$-u'(r)$
, satisfies
![]() $j(r)/u(r)=-\Phi '(r)/\Phi (r)=-u_0/a_1$
(constant). This may be interpreted as a physical generalisation of a Newtonian cooling law. Whereas the heat flux potential is
$j(r)/u(r)=-\Phi '(r)/\Phi (r)=-u_0/a_1$
(constant). This may be interpreted as a physical generalisation of a Newtonian cooling law. Whereas the heat flux potential is
![]() $u(\theta )$
, the inward heat flow at the boundary is proportional to the potential difference between the local temperature and that of a remote inner point. However, the inward heat flow through a finite boundary is not sufficient to prevent unbounded temperature rise due to combustion throughout the entire external region of infinite area.
$u(\theta )$
, the inward heat flow at the boundary is proportional to the potential difference between the local temperature and that of a remote inner point. However, the inward heat flow through a finite boundary is not sufficient to prevent unbounded temperature rise due to combustion throughout the entire external region of infinite area.
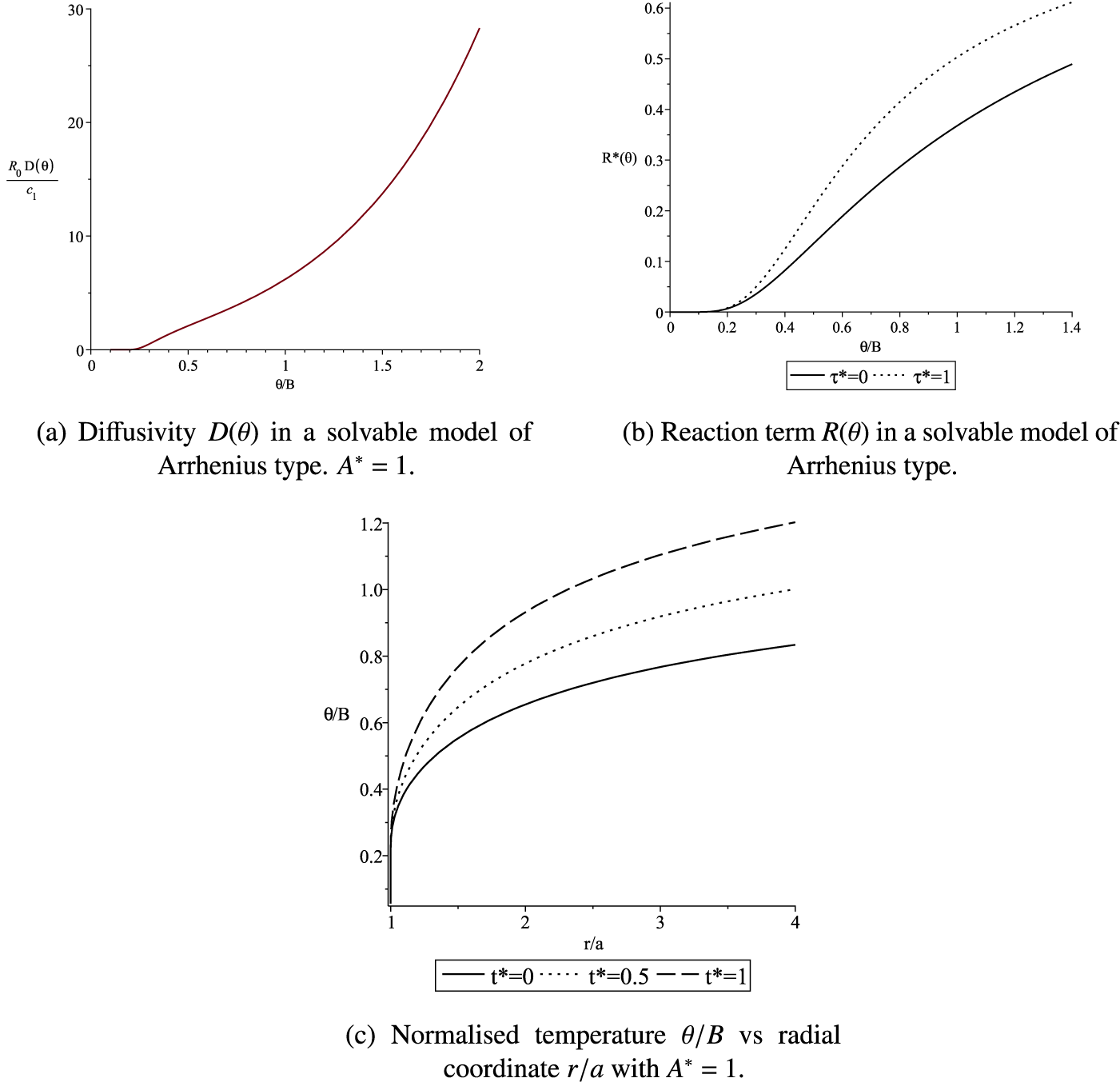
Figure 3 Solvable model of Arrhenius type.
In addition to the delay
![]() $\tau $
between setting up a density gradient and establishing a flux, there is a separate delay
$\tau $
between setting up a density gradient and establishing a flux, there is a separate delay
![]() $\tau _2$
between changing a density and changing a reaction rate before a sufficiently energetic collision takes place to overcome the activation energy. At first order in both
$\tau _2$
between changing a density and changing a reaction rate before a sufficiently energetic collision takes place to overcome the activation energy. At first order in both
![]() $\tau $
and
$\tau $
and
![]() $\tau _2$
,
$\tau _2$
,
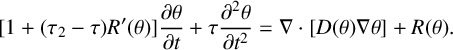 $$ \begin{align} [1+(\tau_2-\tau)R'(\theta)]\frac{\partial \theta}{\partial t}+\tau \frac{\partial^2 \theta}{\partial t^2}=\nabla\cdot[D(\theta)\nabla\theta]+R(\theta). \end{align} $$
$$ \begin{align} [1+(\tau_2-\tau)R'(\theta)]\frac{\partial \theta}{\partial t}+\tau \frac{\partial^2 \theta}{\partial t^2}=\nabla\cdot[D(\theta)\nabla\theta]+R(\theta). \end{align} $$
Since in the absence of harvesting, epidemics and environmental disasters, it normally takes several generations for a population growth rate to change appreciably, it is assumed that both
![]() $\tau R'(\theta )$
and
$\tau R'(\theta )$
and
![]() $\tau _2 R'(\theta )$
are small compared to 1. Equation (1.1) may result from the approximation
$\tau _2 R'(\theta )$
are small compared to 1. Equation (1.1) may result from the approximation
![]() $\tau _2=\tau $
. However, at temperatures well below observed ignition temperatures, the delay
$\tau _2=\tau $
. However, at temperatures well below observed ignition temperatures, the delay
![]() $\tau _2$
may be considerably longer than
$\tau _2$
may be considerably longer than
![]() $\tau $
. In applications to populations, an alternative approximation
$\tau $
. In applications to populations, an alternative approximation
![]() $\tau _2=0$
is implicit in the reaction-telegraph equation studied in [Reference Alharbi and Petrovskii1, Reference Cirilo, Petrovskii, Romeiro and Natti13]. This may apply to some single-cell organisms that multiply rapidly. In that case, the critical domain size increases with
$\tau _2=0$
is implicit in the reaction-telegraph equation studied in [Reference Alharbi and Petrovskii1, Reference Cirilo, Petrovskii, Romeiro and Natti13]. This may apply to some single-cell organisms that multiply rapidly. In that case, the critical domain size increases with
![]() $\tau $
[Reference Alharbi and Petrovskii1]. For vertebrates with a long gestation period, typically
$\tau $
[Reference Alharbi and Petrovskii1]. For vertebrates with a long gestation period, typically
![]() $\tau _2>\tau $
.
$\tau _2>\tau $
.
6 Discussion and conclusion
Physical fields that depend on both space and time generally evolve according to PDEs. Most exact solution methods involve reduction to an ordinary differential equation after assuming some symmetry. The most familiar solutions obtained in this way are steady states, uniform states, travelling waves, radial solutions and scale-invariant similarity solutions. For the applicable class of nonlinear PDEs studied here, another type of solution is available, that is, a solution with functional separation in which the time dependence is exponential:
![]() $u(\theta )=e^{At}\Phi (x)$
. The reduction is associated with a nonclassical symmetry that does not leave the governing PDE invariant, unless an extra algebraic constraint is added among the coefficient functions. Somewhat surprisingly, the constraint allows an exact solution to be constructed from any solution
$u(\theta )=e^{At}\Phi (x)$
. The reduction is associated with a nonclassical symmetry that does not leave the governing PDE invariant, unless an extra algebraic constraint is added among the coefficient functions. Somewhat surprisingly, the constraint allows an exact solution to be constructed from any solution
![]() $\Phi (x)$
to the linear Helmholtz equation. That means that this class of nonlinear PDE is conditionally integrable, yielding an infinite-dimensional space of exact solutions, albeit not the whole set of solutions. The general classification of conditionally integrable PDEs remains largely unexplored.
$\Phi (x)$
to the linear Helmholtz equation. That means that this class of nonlinear PDE is conditionally integrable, yielding an infinite-dimensional space of exact solutions, albeit not the whole set of solutions. The general classification of conditionally integrable PDEs remains largely unexplored.
In particular, in this article, we have concentrated on nonlinear hyperbolic reaction-diffusion equations in two space dimensions, for which, to our knowledge, no space–time-dependent exact solutions have been seen before. In recent times, such equations have been associated with speed-limited diffusion due to a delay
![]() $\tau $
between gradients and fluxes. For reaction-diffusion equations of Fisher–KPP type modified by sufficiently small
$\tau $
between gradients and fluxes. For reaction-diffusion equations of Fisher–KPP type modified by sufficiently small
![]() $\tau $
, we produced an exact solution approaching extinction due to lethal boundary conditions on the boundary of a circular domain, that is, not just the small-
$\tau $
, we produced an exact solution approaching extinction due to lethal boundary conditions on the boundary of a circular domain, that is, not just the small-
![]() $\theta $
approximation but the full nonlinear solution. It is well known from population models that such a solution exists only when the domain is smaller than some critical size. Importantly, we showed that the critical domain size does not depend on
$\theta $
approximation but the full nonlinear solution. It is well known from population models that such a solution exists only when the domain is smaller than some critical size. Importantly, we showed that the critical domain size does not depend on
![]() $\tau $
, therefore, it does not depend on the speed limit.
$\tau $
, therefore, it does not depend on the speed limit.
For population models of Huxley type with weak Allee effect, we again produced an extinction-bound solution within a circle when
![]() $\tau>0$
. For this type of model, the linear approximation near the extinction point has zero reaction, so linear stability analysis is not useful for determining the critical domain size. There have been some general qualitative results in that direction, but explicit results on critical domain size are lacking. Such results would be useful for conservation of invertebrate species, such as queen conch that exhibit an Allee effect [Reference Stoner and Ray-Culp40]. When gestation time is large compared to the mobility delay, the governing equation is modified to equation (5.1). The consequences of the gestation delay will be investigated in the future.
$\tau>0$
. For this type of model, the linear approximation near the extinction point has zero reaction, so linear stability analysis is not useful for determining the critical domain size. There have been some general qualitative results in that direction, but explicit results on critical domain size are lacking. Such results would be useful for conservation of invertebrate species, such as queen conch that exhibit an Allee effect [Reference Stoner and Ray-Culp40]. When gestation time is large compared to the mobility delay, the governing equation is modified to equation (5.1). The consequences of the gestation delay will be investigated in the future.
For a reaction-diffusion model of single-component combustion, we produced an exact finite-valued but unbounded solution with
![]() $\tau>0$
. In the limit
$\tau>0$
. In the limit
![]() $\tau \to 0$
, this reduces to the only known exact solution with standard Arrhenius reaction. When
$\tau \to 0$
, this reduces to the only known exact solution with standard Arrhenius reaction. When
![]() $\tau $
takes realistic small positive values, the relative change to the standard reaction term is bounded and small. As with the actual Arrhenius reaction term that is bounded, blow-up occurs in infinite time, not in finite time as occurs in models with artificial unbounded reaction terms.
$\tau $
takes realistic small positive values, the relative change to the standard reaction term is bounded and small. As with the actual Arrhenius reaction term that is bounded, blow-up occurs in infinite time, not in finite time as occurs in models with artificial unbounded reaction terms.