Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T10:11:54.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical values for a nonlinear difference equation

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theoretical Physics, Research School of Physical Sciences, Australian National University, G.P.O. Box 4, Canberra, A.C.T.2601.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper discusses equilibrium solutions and solutions with period two and period three for the difference equation

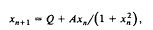
where Q and A are real, positive parameters. The equation was used by Bier and Bountis [1] as an example of a difference equation whose iteration diagram can show bubbles of finite length rather than the successive bifurcations usually expected. The paper examines in more detail what kind of solution can occur for given values of Q and A and establishes a series of critical curves which demarcate the regions in the (Q, A) plane where solutions of period two or period three occur and the subregions where these periodic solutions are stable. This makes it easy to see how Q and A can be combined into a one-parameter equation which gives a bubble, or a series of bubbles, in the iteration diagram.

Type
Research Article
Information
The ANZIAM Journal , Volume 28 , Issue 3 , January 1987 , pp. 340 - 361
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Bier, M. and Bountis, T. C., “Remerging Feigenbaum trees in dynamical systems”, Phys. Lett. A. 104 (1984), 239–244.CrossRefGoogle Scholar
[2]Brown, A., “A nonlinear difference equation with two parameters”, J. Austral. Math. Soc. Ser. B 26 (1985), 430–451.CrossRefGoogle Scholar
[3]Brown, A., “A nonlinear difference equation with two parameters–II”, J. Austral. Math. Soc. Ser. B 27 (1985), 145–166.CrossRefGoogle Scholar
[4]Cascais, J., Dilao, R. and da Costa, A. Noronha, “Chaos and reverse bifurcation in a RCL circuit”, Phys. Lett. A 93 (1983), 213–216.CrossRefGoogle Scholar
[5]Collet, P. and Eckmann, J. P., Iterated maps on the interval as dynamical systems (Birkhäuser, Boston, 1980).Google Scholar
[6]Coppel, W. A., “The solution of cubic equations by iteration”, Z. Angew. Math. Phys. 9a (1958), 380–383.CrossRefGoogle Scholar
[7]Klinker, T., Meyer-Ilse, W. and Lauterborn, W., “Period doubling and chaotic behaviour in a driven Toda oscillator,” Phys. Lett. A 101 (1984), 371–375.CrossRefGoogle Scholar
[8]May, R. M., “Simple mathematical models with very complicated dynamics”, Nature 261 (1976), 459–467.CrossRefGoogle ScholarPubMed
[9]MacDuffee, C. C., Theory of equations (Wiley, New York, 1954), 77.CrossRefGoogle Scholar
[10]Oppo, G. L. and Politi, A., “Collisions of Feigenbaum cascades”, Phys. Rev. A 30 (1984), 435–441.CrossRefGoogle Scholar