Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T07:32:53.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical point behaviour of the diffusion length for radiative transfer

Published online by Cambridge University Press:  17 February 2009

I. F. Grant  and
B. H. J. McKellar
I. F. Grant
Affiliation:
Physics (RAAF) Department, University of Melbourne, Parkville, Vic 3052, Australia
B. H. J. McKellar
Affiliation:
School of Physics, University of Melbourne, Parkville, Vic 3052, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Critical point behaviour of the diffusion length γ for the solutions of the radiative transfer equation deep in a homogenous medium is studied. The Legendre expansion of the medium's phase function P(cos ψ) is taken to be an infinite series and is characterized by the parameters h0, h1h2,…. A characteristic equation for γ is given in terms of an infinite continued fraction. From this equation it is shown that as any one of the hn, say hp, approaches zero, the others being held constant, γ behaves as 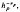, where the critical exponent is found to be vp = ½ for all p = 0, 1, 2,….

Type
Research Article
Information
The ANZIAM Journal , Volume 27 , Issue 2 , October 1985 , pp. 245 - 257
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Chandrasekhar, S., Radiative transfer, (Dover Publications, New York, 1960).Google Scholar
[2]Chu, C-M and Churchill, S. W., ‘Representation of the angular distribution scattered by a spherical particle’, J. Opt. Soc. Amer. 45 (1955), 958–962.CrossRefGoogle Scholar
[3]Hobson, E. W., The theory of spherical and ellipsoidal harmonics (Cambridge University Press 1931) Chapter VII.Google Scholar
[4]van de Hulst, H. C., ‘The spectrum of the anisotropic transfer equation’, Astronom. and Astrophys. 9 (1970), 366–373.Google Scholar
[5]Inonu, E., ‘Scaling and time reversal for the linear monoenergetic Boltzmann equation’, in Topics in mathematical physics (eds. Odabasi, H. and Akyuz, O.), (Colorado Associated University Press, 1977), 127–133.Google Scholar
[6]Kuscer, I., ‘Milne's problem for anisotropic scattering’, J. Math. Phys. 34 (1955), 256–266.CrossRefGoogle Scholar
[7]Lang, K. R., Astrophysical formulae, (Springer-Verlag, Berlin 1974) Sec. 2.7.CrossRefGoogle Scholar
[8]McKellar, B. H. J. and Box, M. A., ‘The scaling group of the radiative transfer equation’, J. Atmospheric Sci. 38 (1981), 1063–1068.2.0.CO;2>CrossRefGoogle Scholar
[9]Martin, A., ‘Analyticity in potential scattering’, Progress in elementary particle and cosmic ray physics, Vol. 8 (eds. Wilson, J. G. and Wonthuysen, S. A.) (North-Holland Publ. Co., Amsterdam, 1965) pp. 1–66.Google Scholar
[10]Martin, A. and Cheung, F., Analyticity properties and bounds of the scattering amplitudes (Gordon and Breach, New York, 1970). See footnote 1, p. 100.Google Scholar
[11]Paltridge, G. W. and Platt, C. M. R., Radiative processes in meteorology and climatology (Elsevier, Amsterdam, 1976) Ch. 2 and 4.Google Scholar
[12]Sobolev, V. V., Radiative transfer (Van Nostrand, Princeton, N.J., 1963).Google Scholar
[13]Stanley, H. E., Introduction to phase transitions and critical phenomena (Clarendon Press, Oxford, 1971).Google Scholar
[14]Wall, H. S., Continued fractions (Van Nostrand, New York, 1948).Google Scholar