Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-17T01:48:57.619Z Has data issue: false hasContentIssue false
  • English
  • Français

The commutation relation i[Y, Z] = 2Y and the absolutely continuous spectrum of Y

Published online by Cambridge University Press:  17 February 2009

J. V. Corbett
J. V. Corbett
Affiliation:
School of Mathematics and Physics, Macquarie University, North Ryde, N. S. W. 2113
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A relation between positive commutators and absolutely continuous spectrum is obtained. If i[Y, Z] = 2Y holds on a core for Z and if Y is positive then we have a system of imprimitivity for the group 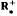on 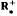, from which it follows that Y has no singular continuous spectrum.

Type
Research Article
Information
The ANZIAM Journal , Volume 23 , Issue 4 , April 1982 , pp. 420 - 427
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Cartier, P., “Quantum mechanical commutation relations and theta functions”, Proc. Sympos. Pure Math. 9 (Amer. Math. Soc., Providence, R. I., 1966), 361–383.Google Scholar
[2]Kato, T., “On the commutation relation AB − BA = C”, Arch. Rat. Mech. Anal. 10 (1962), 273–275.Google Scholar
[3]Kato, T., “Scattering theory”, in Studies in applied mathematics, (ed. Taub, A. H.) (Math. Assoc. Amer., Buffalo, N. Y., 1971).Google Scholar
[4]Mackey, G., “A theorem of Stone and von Neumann”, Duke Math. J. 16 (1949), 313–326.CrossRefGoogle Scholar
[5]Nelson, E., “Analytic vectors”, Ann. of Math. 70 (1959), 572–615.CrossRefGoogle Scholar