Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T11:10:50.316Z Has data issue: false hasContentIssue false
  • English
  • Français

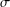CHARACTERIZATIONS OF THE BOREL $\unicode[STIX]{x1D70E}$-FIELDS OF THE FUZZY NUMBER SPACE

Part of: Real functions: Miscellaneous topics Miscellaneous topics in measure theory

Published online by Cambridge University Press:  15 May 2017

TAI-HE FAN Open the ORCID record for TAI-HE FAN [Opens in a new window]  and
MENG-KE BIAN Open the ORCID record for MENG-KE BIAN [Opens in a new window]
TAI-HE FAN*
Affiliation:
Faculty of Sciences, Zhejiang Sci-Tech university, Hangzhou, 310018, China email [email protected]
MENG-KE BIAN
Affiliation:
College of Mobile Telecommunications, Chongqing University of Posts and Telecom, Chongqing, 401520, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we characterize Borel 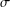$\unicode[STIX]{x1D70E}$-fields of the set of all fuzzy numbers endowed with different metrics. The main result is that the Borel 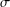$\unicode[STIX]{x1D70E}$-fields with respect to all known separable metrics are identical. This Borel field is the Borel 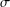$\unicode[STIX]{x1D70E}$-field making all level cut functions of fuzzy mappings from any measurable space to the fuzzy number space measurable with respect to the Hausdorff metric on the cut sets. The relation between the Borel 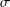$\unicode[STIX]{x1D70E}$-field with respect to the supremum metric 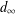$d_{\infty }$ is also demonstrated. We prove that the Borel field is induced by a separable and complete metric. A global characterization of measurability of fuzzy-valued functions is given via the main result. Applications to fuzzy-valued integrals are given, and an approximation method is presented for integrals of fuzzy-valued functions. Finally, an example is given to illustrate the applications of these results in economics. This example shows that the results in this paper are basic to the theory of fuzzy-valued functions, such as the fuzzy version of Lebesgue-like integrals of fuzzy-valued functions, and are useful in applied fields.

Keywords

fuzzy mappingBorel 𝜎-field on fuzzy number spacemeasurability of fuzzy-valued function

MSC classification

Primary: 26E50: Fuzzy real analysis
Secondary: 28E10: Fuzzy measure theory 90C70: Fuzzy programming
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 3-4 , April 2017 , pp. 265 - 275
Copyright
© 2017 Australian Mathematical Society 

References

Butnariu, D., “Measurability concepts for fuzzy mappings”, Fuzzy Sets and Systems 31 (1989) 77–82; doi:10.1016/0165-0114(89)90068-7.Google Scholar
Castaing, C. and Valadier, M., Convex analysis and measurable multifunctions, Volume 580 of Lect. Notes in Math. (Springer, Berlin, 1977); doi:10.1007/BFb0087685.Google Scholar
Diamond, P. and Kloeden, P., Metric spaces of fuzzy sets, theory and applications (World Scientific, Singapore, 1994).Google Scholar
Fan, T. H., “Equivalence of weak convergence and endograph metric convergence for fuzzy number spaces”, in: Fuzzy logic, soft computing, and computational intelligence, Proc. 11th Int. Fuzzy Systems Association World Congr., Beijing (Tsinghua University Press, Beijing, 2005) 41–49.Google Scholar
Fan, T. H. and Wang, G. J., “Endographic approach on supremum and infimum of fuzzy numbers”, Inform. Sci. 159 (2004) 221–231; doi:10.1016/j.ins.2003.08.008.CrossRefGoogle Scholar
Joo, S. Y. and Kim, Y. K., “The Skorokhod topology on space of fuzzy numbers”, Fuzzy Sets and Systems 111 (2000) 497–501; doi:10.1016/S0165-0114(98)00185-7.Google Scholar
Kaleva, O., “Fuzzy differential equations”, Fuzzy Sets and Systems 24 (1987) 301–317; doi:10.1007/978-3-642-35221-8_9.Google Scholar
Kim, Y. K., “Measurability for fuzzy valued functions”, Fuzzy Sets and Systems 129 (2002) 105–109; doi:10.1016/S0165-0114(01)00121-X.CrossRefGoogle Scholar
Luo, C. Z. and Han, L. Y., “Fuzzy representation of firm’s demands under the soft budget constraints”, Fuzzy Systems Math. 1 (1987) 127–134; http://www.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD$&$filename=MUTE198700020$&$dbname=CJFD8589.Google Scholar
Zhang, B. K., “On measurability of fuzzy-number-valued functions”, Fuzzy Sets and Systems 120 (2001) 505–509; doi:10.1016/S0165-0114(99)00061-5.CrossRefGoogle Scholar