Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T18:42:10.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Bubbles rising in an inclined two-dimensional tube and jets falling along a wall

Published online by Cambridge University Press:  17 February 2009

J. Lee  and
J.-M. Vanden-Broeck
J. Lee
Affiliation:
Department of Mathematics, Kwang Woon University, Wolgye-dong Nowon-Gu, Seoul 139–701, Korea
J.-M. Vanden-Broeck
Affiliation:
Department of Mathematics and Center for the Mathematical SciencesUniversity of Wisconsin-Madison, Madison, WI 53706
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The motion of a two-dimensional bubble rising at a constant velocity U in an inclined tube of width H is considered. The bubble extends downwards without limit, and is bounded on the right by a wall of the tube, and on the left by a free surface. The same flow configuration describes also a jet emerging from a nozzle and falling down along an inclined wall. The acceleration of gravity g and the surface tension T are included in the free surface condition. The problem is characterized by the Froude number 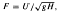the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained via series truncation for all values of 0 < β < π. The results extend previous calculations of Vanden-Broeck [12–14] for β = π/2 and of Couët and Strumolo [3] for 0 < β < π/2. It is found that the behavior of the solutions depends on whether 0 < β 2π/3 or 2π/3 ≤ β < π. When T = 0, it is shown that there is a critical value F of Froude number for each 0 < β 2π/3 such that solutions with γ = 0, π/3 and π - β occur for F > Fc F = Fc and F < Fc respectively, and that all solutions are characterized by γ = 0 for 2π/3 ≤ β < π. When a small amount of surface tension T is included in the free surface condition, it is found that for each 0 < β < π there exists an infinite discrete set of values of F for which γ = π - β. A particular value F* of the Froude number for which T = 0 and γ = π - β is selected by taking the limit as T approaches zero. The numerical values of F* and the corresponding free surface profiles are found to be in good agreement with experimental data for bubbles rising in an inclined tube when 0 < β < π/2.

Type
Research Article
Information
The ANZIAM Journal , Volume 39 , Issue 3 , January 1998 , pp. 332 - 349
Copyright
Copyright © Australian Mathematical Society 1998

References

[1] Birkhoff, G. and Carter, D., “Rising plane bubbles”, J. Math. and Mech. 6 (1957) 769–779.Google Scholar
[2] Collins, R., “A simple model of a plane gas bubble in a finite liquid”, J. Fluid Mech. 22 (1965) 763–771.CrossRefGoogle Scholar
[3] Couët, B. and Strumolo, G. S., “The effects of surface tension and tube inclination on a two-dimensional rising bublle”, J. Fluid Mech. 184 (1987) 1–14.CrossRefGoogle Scholar
[4] Dias, F. and J.-M. Vanden-Broeck, “Flows emerging from a nozzle and falling under gravity”, J. Fluid Mech. 213 (1990) 465–477.CrossRefGoogle Scholar
[5] Garabedian, P. R., “On steady-state bubble generated by taylor instability”, Proc. R. Soc. London Ser. A 241 (1957) 423–43.Google Scholar
[6] Keller, J. B., “Teapot effect”, J. Appl. Phys. 28 (1957) 859–864.CrossRefGoogle Scholar
[7] Keller, J. B. and Gee, J., “Flows of thin streams with free boundaries”, J. Fluid Mech. 59 (1973) 417–432.CrossRefGoogle Scholar
[8] Lee, J. and Vanden-Broeck, J.-M., “Two-dimensional jets falling from funnels and nozzles”, Phys. Fluids A 5 (1993) 2454–2460.CrossRefGoogle Scholar
[9] Maneri, C. C., “The motion of plane bubbles in inclined ducts”, Ph. D. Thesis, Polytechnic Institute of Brooklyn, New York.Google Scholar
[10] Reiner, M., “The teapot effect…a problem”, Phys. Today 9 (1956) 16–20.CrossRefGoogle Scholar
[11] Tuck, E.O., “Efflux from a slit in a vertical wal”, J. Fluid Mech. 1987 (1987) 253–264.CrossRefGoogle Scholar
[12] Vanden-Broeck, J.-M., “Bubbles rising in a tube and jets falling from a nozzle”, Phys. Fluids 27 (1984) 1090–1093.CrossRefGoogle Scholar
[13] Vanden-Broeck, J.-M., “Rising bubbles in a tube with surface tension”, Phys. Fluids 27 (1984) 2604–2607.CrossRefGoogle Scholar
[14] Vanden-Broeck, J.-M., “Pointed bubbles rising in a two-dimensional tube”, Phys. Fluids 29 (1986) 1343–1344.CrossRefGoogle Scholar
[15] Vanden-Broeck, J.-M. and Keller, J. B., “Pouring flows”, Phys. Fluids 29 (1986) 3958–3961.CrossRefGoogle Scholar
[16] Vanden-Broeck, J.-M. and Keller, J. B., “Pouring flows with separation”, Phys. Fluids A 1 (1989) 156–158.CrossRefGoogle Scholar
[17] Vanden-Broeck, J.-M. and Tuck, E. O., “Flow near the intersection of a free surface with a vertical wall”, SIAM J. Appl. Math. 54 (1954) 1–13.CrossRefGoogle Scholar