The asymptotic properties of solutions of the non-linear eigenvalue problem, associated with the homogeneoud Dirichlet problem for

are investigated. Here f and g are smooth functions of position in a finite plane region with a smooth boundary. The results for the positive solution are well established, but knowledge of other branches of solutions is scarce. Here positive solutions are pieced together across lines partitioning the domain, and variational arguments are framed, as an effective means of locating the lines, so that the composite function is everywhere a solution of *. Heuristic arguments suggest strongly that there is a close relationship between the nodal lines of * and certain classes of weighted geodesic lines defined by the classical variational problem for the functional

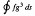
which provides an effective basis for computation. Some results are proved but others remain conjectures. Analogous results are proved for the associated ordinary differential equation. The geometry of the solutions is surprisingly restricted when the coefficients are spatially variable. The arguments are extended to a class of reactive, diffusive systems. It is possible to predict the pattern of domains of different outcomes in terms of properties of the surface on which the reactions occur, without a knowledge of the chemical kinetics. The results appear to provide a basis for stringent testing of the postulated role of reactive-diffusive mechanisms in the formation of complex patterns in biological species.