Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T11:03:22.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behavior of solutions to the Stefan problem with a kinetic condition at the free boundary

Published online by Cambridge University Press:  17 February 2009

J. N. Dewynne ,
S. D. Howison ,
J. R. Ockendon  and
Weiqing Xie
J. N. Dewynne
Affiliation:
Mathematical Institute, 24–29 St. Giles, Oxford OX1 3LB, U. K.
S. D. Howison
Affiliation:
Mathematical Institute, 24–29 St. Giles, Oxford OX1 3LB, U. K.
J. R. Ockendon
Affiliation:
Mathematical Institute, 24–29 St. Giles, Oxford OX1 3LB, U. K.
Weiqing Xie
Affiliation:
Mathematical Institute, 24–29 St. Giles, Oxford OX1 3LB, U. K.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the large time behaviour of the free boundary for a one-phase Stefan problem with supercooling and a kinetic condition u = −ε|⋅ṡ| at the free boundary x = s(t). The problem is posed on the semi-infinite strip [0,∞) with unit Stefan number and bounded initial temperature ϕ(x) ≤ 0, such that ϕ → −1 − δ as x → ∞, where δ is constant. Special solutions and the asymptotic behaviour of the free boundary are considered for the cases ε ≥ 0 with δ negative, positive and zero, respectively. 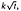We show that, for ε > 0, the free boundary is asymptotic to , δt/ε if < δ > 0 respectively, and that when δ = 0 the large time behaviour of the free boundary depends more sensitively on the initial temperature. We also give a brief summary of the corresponding results for a radially symmetric spherical crystal with kinetic undercooling and Gibbs-Thomson conditions at the free boundary.

Type
Research Article
Information
The ANZIAM Journal , Volume 31 , Issue 1 , July 1989 , pp. 81 - 96
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Carslaw, H. S. and Jaeger, J. C., Conduction of heat in solids (Oxford University Press, 1959).Google Scholar
[2]Chadam, J., Howison, S. D. and Ortoleva, P., “Existence and stability for spherical crystals growing in a supersaturated solution”, IMA J. Appl. Math. 39 (1987) 1–15.CrossRefGoogle Scholar
[3]Chadam, J. and Ortoleva, P., “The stability effect of surface tension on the development of the free boundary in a planar, one-dimensional, Cauchy-Stefan problem”, IMA J. Appl. Math. 30 (1983) 57–66.CrossRefGoogle Scholar
[4]Copson, E. T., Asymptotic expansions (Cambridge University Press, 1965).CrossRefGoogle Scholar
[5]Coriell, S. R. and Sekerka, R. F., “Oscillatory morphological instabilities due to nonequilib-rium segregation’, J. Crystal Growth 61 (1983) 499–508.CrossRefGoogle Scholar
[6]Crowley, A. B., “Some remarks on non-equilibrium solidification problems”, in Free and moving boundary problems, (eds. Hoffman, K. H. and Sprekels, J.), (Pitman, 1989).Google Scholar
[7]Fasano, A. and Primicerio, M., “New results on some classical parabolic free boundary problems”, Quart. Appl. Math. 38 (1981) 439–460.CrossRefGoogle Scholar
[8]Garinberg, G. A. and Chekmareva, O. M., “Motion of phase interface in Stefan problems”, Sov. Phys. Tech. Phys. 15 (1971) 1579.Google Scholar
[9]Howison, S. D., Ockendon, J. R. and Lacey, A. A., “Singularity development in moving boundary problems”, Quart. J. Mech. Appl. Math. 38 (1985) 343–360.CrossRefGoogle Scholar
[10]Krukowski, S. and Turski, L. A., “Time-dependent solution for a spherically symmetric freezing precipitate”, J. Crystal Growth 58 (1982) 631–635.CrossRefGoogle Scholar
[11]Lacey, A. A. and Ockendon, J. R., “Ill-posed boundary problems”, Control Cybernet. 14 (1985) 275–296.Google Scholar
[12]Lamé, G. and Clapeyron, B. P., “Memoire sur la solidification par refroidissement d'un globe liquide”, Annates Chimie Physique 47 (1831) 250–256.Google Scholar
[13]Schaefer, R. J. and Glicksman, M. E., “Fully time-dependent theory for the growth of spherical crystal nuclei”, J. Crystal Growth 5 (1969) 44–58.CrossRefGoogle Scholar
[14]Visintin, A., “Stefan problem with a kinetic condition at the free boundary”, Ann. Math. Pura Appl. (to appear).Google Scholar
[15]Xie, W., The Stefan problem with a kinetic condition at the free boundary, PreprintGoogle Scholar