Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T10:41:15.970Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATING THE KOHLRAUSCH FUNCTION BY SUMS OF EXPONENTIALS

Part of: Computational aspects Numerical approximation and computational geometry Integral equations, integral transforms Miscellaneous topics in measure theory

Published online by Cambridge University Press:  04 September 2013

MIN ZHONG ,
R. J. LOY  and
R. S. ANDERSSEN
MIN ZHONG*
Affiliation:
School of Mathematical Sciences, Fudan University, 200433 Shanghai, People’s Republic of China
R. J. LOY*
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 0200, Australia
R. S. ANDERSSEN*
Affiliation:
CSIRO Mathematics, Informatics and Statistics, GPO Box 664, Canberra, ACT 2601, Australia
*
✉[email protected]
✉[email protected]
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Kohlrausch functions 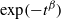$\exp (- {t}^{\beta } )$, with 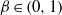$\beta \in (0, 1)$, which are important in a wide range of physical, chemical and biological applications, correspond to specific realizations of completely monotone functions. In this paper, using nonuniform grids and midpoint estimates, constructive procedures are formulated and analysed for the Kohlrausch functions. Sharper estimates are discussed to improve the approximation results. Numerical results and representative approximations are presented to illustrate the effectiveness of the proposed method.

Keywords

Kohlrausch functionsums of exponentialsapproximation

MSC classification

Secondary: 65D20: Computation of special functions, construction of tables 28E99: None of the above, but in this section 33F05: Numerical approximation and evaluation 65R10: Integral transforms
Type
Research Article
Information
The ANZIAM Journal , Volume 54 , Issue 4 , April 2013 , pp. 306 - 323
Copyright
Copyright ©2013 Australian Mathematical Society 

References

Anderssen, R. S., Davies, A. R. and de Hoog, F. R., “On the interconversion integral equation for relaxation and creep”, ANZIAM J. 48 (2007) C34–C266; http://journal.austms.org.au/ojs/index.php/ANZIAMJ/article/view/64.Google Scholar
Anderssen, R. S., Davies, A. R. and de Hoog, F. R., “On the sensitivity of interconversion between relaxation and creep”, Rheol. Acta 47 (2008) 159–167; doi:10.1007/s00397-007-0223-6.CrossRefGoogle Scholar
Anderssen, R. S., Davies, A. R. and de Hoog, F. R., “On the Volterra integral equation relating creep and relaxation”, Inverse Problems 24 (2008) 035009; doi:10.1088/0266-5611/24/3/035009.CrossRefGoogle Scholar
Anderssen, R. S., Edwards, M. P., Husain, S. A. and Loy, R. J., “Sums of exponentials approximations for the Kohlrausch function”, in: MODSIM2011, 19th International Congress on Modelling and Simulation (eds Chan, F., Marinova, D. and Anderssen, R. S.) (Modelling and Simulation Society of Australia and New Zealand, 2011), 263–369; http://www.mssanz.org.au/modsim2011/A3/anderssen.pdf.Google Scholar
Anderssen, R. S., Husain, S. A. and Loy, R. J., “The Kohlrausch function: properties and applications”, ANZIAM J. 45 (2004) C800–C816; http://journal.austms.org.au/ojs/index.php/ANZIAMJ/article/view/924.CrossRefGoogle Scholar
Berberan-Santos, M. N., “Analytical inversion of the Laplace transform without contour integration: application to luminescence decay laws and other relaxation functions”, J. Math. Chem. 38 (2005) 165–173; doi:10.1007/s10910-005-4961-3.CrossRefGoogle Scholar
Berberan-Santos, M. N., Bodunov, E. N. and Valeur, B., “Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential)”, Chem. Phys. 315 (2005) 171–182; doi:10.1016/j.chemphys.2005.04.006.CrossRefGoogle Scholar
de Gennes, P.-G., “Relaxation anomalies in linear polymer melts”, Macromolecules 35 (2002) 3785–3786; doi:10.1021/ma012167y.CrossRefGoogle Scholar
Feller, W., An introduction to probability theory and its applications, Volume II (Wiley, New York, 1966).Google Scholar
Lindsey, C. P. and Patterson, G. D., “Detailed comparison of the Williams–Watts and Cole–Davidson functions”, J. Chem. Phys. 73 (1980) 3348–3357; doi:10.1063/1.440530.CrossRefGoogle Scholar
Liu, Y., “Approximation by Dirichlet series with nonnegative coefficients”, J. Approx. Theory 112 (2001) 226–234; doi:10.1006/jath.2001.3589.CrossRefGoogle Scholar
Loy, R. J. and Anderssen, R. S., On the construction of Dirichlet series approximations for completely monotone functions, Math. Comp. to appear; doi:10.1090/S0025-5718-2013-02725-1.CrossRefGoogle Scholar
Macdonald, J. R., “Accurate fitting of immittance spectroscopy frequency-response data using the stretched exponential model”, J. Non-Cryst. Solids 212 (1997) 95–116; doi:10.1016/S0022-3093(96)00657-6.CrossRefGoogle Scholar
Macdonald, J. R., “Surprising conductive- and dielectric-system dispersion differences and similarities for two Kohlrausch-related relaxation-time distributions”, J. Phys.: Condens. Matter. 18 (2006) 629–644; doi:10.1088/0953-8984/18/2/019.Google Scholar
Montroll, E. W. and Bendler, J. T., “On Lévy (or stable) distributions and the Williams–Watts model of dielectric relaxation”, J. Stat. Phys. 34 (1984) 129–162; doi:10.1007/BF01770352.CrossRefGoogle Scholar
Ngai, K. L. and Roland, C. M., “Development of cooperativity in the local segmental dynamics of (poly)vinylacetate: synergy of thermodynamics and intermolecular coupling”, Polymer 43 (2002) 567–573; doi:10.1016/S1089-3156(01)00011-3.CrossRefGoogle Scholar
Nikonov, A., Davies, A. R. and Emri, I., “The determination of creep and relaxation functions from a single experiment”, J. Rheol. 49 (2005) 1193–1211; doi:10.1122/1.2072027.CrossRefGoogle Scholar
Penson, K. A. and Górska, K., “Exact and explicit probability densities for one-sided Lévy stable distributions”, Phys. Rev. Lett. 105 (2010) 210604; doi:10.1103/PhysRevLett.105.210604.CrossRefGoogle ScholarPubMed
Pollard, H., “The representation of ${e}^{- {x}^{\lambda } } $ as a Laplace integral”, Bull. Amer. Math. Soc. 52 (1946) 908–910; doi:10.1090/S0002-9904-1946-08672-3.CrossRefGoogle Scholar
Rambousky, R., Weiss, M., Mysz, H., Moske, M. and Samwer, K., “Structural relaxation and viscous flow in amorphous ZrAlCu above and below the glass transition temperature”, Mater. Sci. Forum 225–227 (1996) 83–88; doi:10.4028/www.scientific.net/MSF.225-227.83.CrossRefGoogle Scholar
Sasaki, N., Nakayama, Y., Yoshikawa, M. and Enyo, A., “Stress relaxation function of bone and bone collagen”, J. Biomechanics 26 (1993) 1369–1376; doi:10.1016/0021-9290(93)90088-V.CrossRefGoogle ScholarPubMed
Shlesinger, M. F. and Montroll, E. W., “On the Williams–Watts function of dielectric relaxation”, Proc. Natl. Acad. Sci. 81 (1984) 1280–1283; doi:10.1073/pnas.81.4.1280.CrossRefGoogle ScholarPubMed