Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T00:39:58.175Z Has data issue: false hasContentIssue false
  • English
  • Français

An expansion of bivariate spline functions

Published online by Cambridge University Press:  17 February 2009

Huan-Wen Liu
Huan-Wen Liu
Affiliation:
School of Mathematics and Applied Statistics, The University of Wollongong, Wollongong, NSW 2522, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ denote a triangulation of a planar polygon Ω. For any positive integer 0 ≤ r < k, let 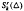denote the vector space of functions in Cr whose restrictions to each triangle of Δ are polynomials of total degree at most k. Such spaces, called bivariate spline spaces, have many applications in surface fitting, scattered data interpolation, function approximation and numerical solutions of partial differential equations. An important problem is to give the function expression. In this paper, we prove that, if (Δ, Ω) is type-X, then any bivariate spline function in 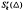can be expressed by a series of univariate polynomials and a special bivariate finite element function in 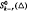satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space 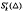. In addition, the dimension of 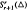for a kind of triangulation has been determined.

Type
Research Article
Information
The ANZIAM Journal , Volume 41 , Issue 4 , April 2000 , pp. 527 - 541
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Alfeld, P., Neamtu, M. and Schumaker, L. L., “Fitting scattered data on sphere-like surfaces using spherical splines”, J. Comp. Appl. Math. 73 (1996) 5–43.CrossRefGoogle Scholar
[2]Alfeld, P., Piper, B. and Schumaker, L. L., “An explicit basis for C 1 quartic bivariate splines”, SIAM J. Numer. Anal. 24 (1987) 891–911.Google Scholar
[3]Alfeld, P. and Schumaker, L. L., “The dimension of bivariate spline spaces of smoothness r for degree d ≥ 4r + 1”, Const. Approx. 3 (1987) 189–197.Google Scholar
[4]de Boor, C., “B-form basis”, in Geometric Modeling (ed. Farin, G.), (SIAM, Philadelphia, 1987) 21–28.Google Scholar
[5]de Boor, C., Hollig, K., Riemenschneider, S. and Ron, A. (eds.), Box splines (Springer-Verlag, New York, 1993).Google Scholar
[6]Chui, C. K. and Wang, J. Z., “On compactly supported spline wavelets and a duality principle”, Trans. Amer. Math. Society 330 (1992) 903–916.Google Scholar
[7]Chui, C. K. and Wang, J. Z., “A cardinal spline approach to wavelets”, Proc. Amer. Math. Society 113 (1991) 785–793.Google Scholar
[8]Chui, C. K. and Wang, R. H., “Multivariate spline spaces”, J. Math. Anal. Appl. 94 (1983) 197–221.Google Scholar
[9]Chui, C. K. and Wang, R. H., “On smooth multivariate spline functions”, Math. Comp. 47 (1983) 131–142.CrossRefGoogle Scholar
[10]Dahmen, W. and Micchelli, C. A., “Recent progress in multivariate splines”, in Approximation theory IV (eds. Chui, C. K., Schumaker, L. L. and Ward, J.) (Academic Press, 1983) 27–121.Google Scholar
[11]Farin, G., “Triangular Bernstein-Bézier patches“. Computer Aided Geometric Design 3 (1986) 87–127.Google Scholar
[12]Farin, G. (eds.), Curves and surfaces for computer aided geometric design, a practical guide (Academic Press, New York, 1988).Google Scholar
[13]Hong, D., “Spaces of bivariate spline functions over triangulations”, Approx. Theory and Appl. 7 (1991) 56–75.Google Scholar
[14]Hong, D., “A new formulation of Bernstein-Bézier based smoothness conditions for pp functions”, Approx. Theory and Appl. 11 (1995) 67–75.Google Scholar
[15]Hong, D. and Liu, H.-W. and Mohapatra, Ram, “Optimal triangulations and smoothness conditions for bivariate splines”, in Approximation theory IX, Vol. 2: Computational Aspects (eds. Chui, C. K., Schumaker, L. L.), (Vanderbilt University Press, Nashville, 1998) 129–136.Google Scholar
[16]Jia, R. Q., “B-net representation of multivariate splines”, Ke Xue Tong Bao (A Monthly Journal of Science) 11 (1987) 804–807.Google Scholar
[17]Jia, R. Q., “A dual basis for the integer translates of an exponential box spline”, The Rocky Mountain Journal of Mathematics 23 (1993) 223–242.CrossRefGoogle Scholar
[18]Li, Y. S. and Guan, L. T., “Bivariate polynomial natural spline interpolation to scattered data”, J. Comp. Math.: An International Journal on Numerical Methods, Analysis and Applications 8 (1990) 135–146.Google Scholar
[19]Liu, H.-W., “The double periodic spline space with degree k ≥ 4 on Type-1 triangulation”, CALCOLO 29 (1992) 269–289.Google Scholar
[20]Liu, H. W., “An integral representation of bivariate splines and the dimension of quadratic spline spaces over stratified triangulation”, Acta Math. Sinica 4 (1994) 534–543.Google Scholar
[21]Liu, H.-W., “The dimension of cubic spline space over stratified triangulation”, J. Math. Research. and Exposition 16 (1996) 199–208.Google Scholar
[22]Morgan, J. and Scott, R., “A nodal basis for C 1 piecewise polynomials of degree n ≥ 5”, Math. Comp. 29 (1975) 736–740.Google Scholar
[23]Morgan, J. and Scott, R., “The dimension of piecewise polynomials”, manuscript.Google Scholar
[24]Schumaker, L. L., “On the dimension of spaces of piecewise polynomials in two variables”, in Multivariable Approximation Theory (eds. Schempp, W. and Zeller, K.), (Birkhäuser, Basel, 1979) 396–412.Google Scholar
[25]Wang, R. H., “The structural characterization and interpolation for multivariate splines”, Acta. Math. Sinica 18 (1975), 91–106.Google Scholar
[26]Zwart, P., “Multivariate splines with non-degenerate partitions”, SIAM J. Numer. Anal. 10 (1973) 665–673.Google Scholar