Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T10:49:59.419Z Has data issue: false hasContentIssue false
  • English
  • Français

An algorithm for constructing biorthogonal multiwavelets with higher approximation orders

Published online by Cambridge University Press:  17 February 2009

Yang Shouzhi
Yang Shouzhi
Affiliation:
Department of Mathematics, Shantou University, Shantou 515063, P. R. China; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a pair of biorthogonal multiscaling functions, we present an algorithm for raising their approximation orders to any desired level. Precisely, let Φ(x) and 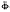(x) be a pair of biorthogonal multiscaling functions of multiplicity r, with approximation orders m and 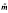, respectively. Then for some integer s, we can construct a pair of new biorthogonal multiscaling functions Φnew(x) = [ΦT (x), φr+1 (x), φr+2(x),… φr+s(x)]T and 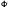new(x) = [ 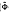(x) T, 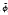r+1(x), 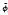r+2(x),… 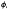r+s(x)]T with approximation orders n (n > m) and ñ (ñ > 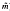), respectively. In addition, corresponding to Φnew(x) and 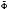new(x) a biorthogonal multiwavelet pair ψnew(x) and 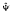new(x) is constructed explicitly. Finally, an example is given.

Keywords

biorthogonalmultiscaling functionsmultiwaveletsapproximation order.
Type
Research Article
Information
The ANZIAM Journal , Volume 47 , Issue 4 , April 2006 , pp. 513 - 526
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Chui, C. K. and Lian, J.-A., “A study on orthonormal multi-wavelets”, Appl. Numer. Math. 20(1996) 273–298.CrossRefGoogle Scholar
[2]Chui, C. K. and Lian, J.-A., “Construction of orthonormal multi-wavelets with additional vanishing moments”, Adv. Comput. Math. 24 (2006) 239–262.CrossRefGoogle Scholar
[3]Cohen, A., Daubechies, I. and Plonka, G., “Regularity of refinable function vectors”, J. Fourier Anal. Appl. 3 (1997) 295–324.CrossRefGoogle Scholar
[4]Dahmen, W. and Micchelli, C. A., “Biorthogonal wavelet expansion”, Constr Approx. 13 (1997) 293–328.CrossRefGoogle Scholar
[5]Heil, C. and Collela, D., “Matrix refinement equations: Existence and uniqueness”, J. Fourier Anal. Appl. 2 (1996) 363–377.Google Scholar
[6]Jiang, Q., “On the regularity of matrix refinable functions”, SIAM J. Math. Anal. Appl. 29 (1998) 1157–1176.CrossRefGoogle Scholar
[7]Jiang, Q., “Orthogonal multiwavelets with optimum time-frequency resolution”, IEEE Trans. Signal Process. 46 (1998) 830–844.CrossRefGoogle Scholar
[8]Lian, J.-A., “On the order of polynomial reproduction for multi-scaling functions”, Appl. Comp. Harm. Anal. 3 (1996) 358–365.CrossRefGoogle Scholar
[9]Lian, J.-A., “Orthogonal criteria for multiscaling functions”, Appl. Comput. Harmon. Anal. 5 (1998) 277–311.CrossRefGoogle Scholar
[10]Lian, J.-A. and Chui, C. K., “Analysis-ready multiwavelets (armlets) for processing scalar-valued signals”, IEEE Trans. Signal Process. Lett. 11 (2004) 205–208.CrossRefGoogle Scholar
[11]Lian, J.-A. and Chui, C. K., “Balanced multiwavelets with short filters”, IEEE Trans. Signal Process. Lett. 11 (2004) 75–78.CrossRefGoogle Scholar
[12]Plonka, G., “Approximation order provided by refinable function vectors”, Constr Approx. 13 (1997) 221–244.CrossRefGoogle Scholar
[13]Plonka, G. and Strela, V., “Construction of multiscaling functions with approximation and symmetry”, SIAM J. Math. Anal. Appl. 29 (1998)481–510.CrossRefGoogle Scholar
[14]Plonka, G. and Strela, V., “From wavelets to multiwavelets”, in Mathematical methods for curves and surfaces, II (eds. Daehlen, M., Lyche, T. and Schumaker, L. L.), (Vanderbilt Univ. Press, Nashville, TN, 1998) 1–25.Google Scholar
[15]Shen, Z., “Refinable function vectors”, SIAM J. Math. Anal. Appl. 29 (1998) 235–250.CrossRefGoogle Scholar
[16]Strela, V., “Multiwavelets: Regularity, orthogonality and symmetry via two-scale similarity transform”, Studies in Appl. Math. 98 (1997) 335–354.CrossRefGoogle Scholar
[17]Yang, S.-Z., “A fast algorithm for constructing orthogonal multiwavelets”, ANZIAM J. 46 (2004)185–202.Google Scholar
[18]Yang, S.-Z. and Cheng, Z.-X., “Orthonormal multi-wavelets on the interval [0, 1] with multiplicity r”, Acta Mathematica Sinica 45 (2002) 789–796.Google Scholar
[19]Yang, S.-Z., Cheng, Z.-X. and Wang, H.-Y., “Construction of biorthogonal multiwavelets”, J. Math. Anal. Appl. 276 (2002) 1–12.CrossRefGoogle Scholar