Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T07:12:27.599Z Has data issue: false hasContentIssue false
  • English
  • Français

HOPF BIFURCATION ANALYSIS OF A FRACTIONAL-ORDER HOLLING–TANNER PREDATOR-PREY MODEL WITH TIME DELAY

Part of: General theory in ordinary differential equations Functional-differential and differential-difference equations

Published online by Cambridge University Press:  05 April 2022

C. CELIK Open the ORCID record for C. CELIK [Opens in a new window]  and
K. DEGERLİ Open the ORCID record for K. DEGERLİ [Opens in a new window]
C. CELIK*
Affiliation:
Faculty of Arts and Sciences, Department of Mathematics, Yildiz Technical University, İstanbul, Turkey
K. DEGERLİ
Affiliation:
Faculty of Engineering and Natural Sciences, Department of Mathematics, Bahcesehir University, İstanbul, Turkey; e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a fractional-order delayed predator-prey model with Holling–Tanner-type functional response. Mainly, by choosing the dela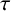y time $\tau $ as the bifurcation parameter, we show that Hopf bifurcation can occur as the delay time 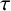$\tau $ passes some critical values. The local stability of a positive equilibrium and the existence of the Hopf bifurcations are established, and numerical simulations for justifying the theoretical analysis are also presented.

Keywords

fractional-ordertime-delayHopf bifurcationpredator-prey system

MSC classification

Primary: 34A08: Fractional differential equations
Secondary: 34K18: Bifurcation theory 34K20: Stability theory
Type
Research Article
Information
The ANZIAM Journal , Volume 64 , Issue 1 , January 2022 , pp. 23 - 39
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angstmann, C. N., Henry, B. I. and McGann, A. V., “A fractional-order infectivity SIR model”, Phys. A 452 (2016) 86–93; doi:10.1016/j.physa.2016.02.029.CrossRefGoogle Scholar
Bhalekar, S. and Daftardar-Gejji, V., “A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order”, J. Fract. Calc. Appl. 1 (2011) 1–9; https://www.researchgate.net/publication/245538900_A_Predictor-Corrector_Scheme_For_Solving_Nonlinear_Delay_Differential_Equations_Of_Fractional_Order.Google Scholar
Bhalekar, S., Daftardar-Gejji, V., Baleanu, D. and Magin, R., “Fractional Bloch equation with delay”, Comput. Math. Appl. 61 (2011) 1355–1365; doi:10.1016/j.camwa.2010.12.079.CrossRefGoogle Scholar
Çelik, C., “The stability and Hopf bifurcation for a predator-prey system with time delay”, Chaos Solitons Fractals 37 (2008) 87–99; doi:10.1016/j.chaos.2007.10.045.CrossRefGoogle Scholar
Çelik, C., “Hopf bifurcation of a ratio-dependent predator-prey system with time delay”, Chaos Solitons Fractals 42 (2009) 474–1484; doi:10.1016/j.chaos.2009.03.071.CrossRefGoogle Scholar
Çelik, C., “Dynamical behavior of a ratio dependent predator-prey system with distributed delay”, Discrete Contin. Dyn. Syst. Ser. B 3 (2011) 719–738; doi:10.3934/dcdsb.2011.16.719.Google Scholar
Çelik, C., “Dynamical analysis of a ratio dependent Holling–Tanner type predator-prey model with delay”, J. Appl. Funct. Anal. 8 (2013) 194–213; https://www.researchgate.net/publication/267673525_Dynamical_analysis_of_a_ratio_dependent_Holling-Tanner_type_predator-prey_model_with_delay.Google Scholar
Çelik, C. and Duman, O., “Allee effect in a discrete-time predator-prey system”, Chaos Solitons Fractals 40 (2009) 1956–1962; doi:10.1016/j.chaos.2007.09.077.CrossRefGoogle Scholar
Chen, X., “Periodicity in a nonlinear discrete predator-prey system with state dependent delays”, Nonlinear Anal. 8 (2007) 435–446; doi:10.1016/j.nonrwa.2005.12.005.CrossRefGoogle Scholar
Chen, Y. Q. and Moore, K. L., “Analytical stability bound for a class of delayed fractional-order dynamic systems”, Nonlinear Dyn. 29 (2002) 191–200; doi:10.1023/A:1016591006562.CrossRefGoogle Scholar
Chen, Y. Q., Vinagre, B. M. and Podlubny, I., “Continued fraction expansion approaches to discretizing fractional order derivatives—an expository review”, Nonlinear Dyn. 38 (2004) 155–170; doi:10.1007/s11071-004-3752-x.CrossRefGoogle Scholar
Deng, W., Li, C. and Lu, J., “Stability analysis of linear fractional differential system with multiple time delays”, Nonlinear Dyn. 48 (2007) 409–416; doi:10.1007/s11071-006-9094-0.CrossRefGoogle Scholar
Fowler, M. S. and Ruxton, G. D., “Population dynamic consequences of Allee effects”, J. Theoret. Biol. 215 (2002) 39–46; doi:10.1006/jtbi.2001.2486.CrossRefGoogle ScholarPubMed
Gopalsamy, K., “Time lags and global stability in two species competition”, Bull. Math. Biol. 42 (1980) 729–737; doi:10.1007/BF02460990.CrossRefGoogle Scholar
Guckenheimer, J. and Holmes, P., Nonlinear oscillations, dynamical systems and bifurcations of vector fields (eds Marsden, J. E. and Sirovich, L.), Volume 42 of Appl. Math. Sci. (Springer, New York, 1983); doi:10.1007/978-1-4612-1140-2.CrossRefGoogle Scholar
Hilfer, R., Applications of fractional calculus in physics (World Scientific, Singapore, 2000); doi:10.1142/3779.CrossRefGoogle Scholar
Huang, C., Song, X., Fang, B., Xiao, M. and Cao, J., “Modeling, analysis and bifurcation control of a delayed fractional-order predator-prey model”, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 28 (2018) 1850118; doi:10.1142/S0218127418501171.CrossRefGoogle Scholar
Izhikevich, E. M., Dynamical systems in neuroscience: the geometry of excitability and bursting (MIT Press, Cambridge, MA, 2007); doi:10.7551/mitpress/2526.001.0001.Google Scholar
Jarad, F., Abdeljawad (Maraaba), T. and Baleanu, D., “Fractional variational principles with delay within Caputo derivatives”, Rep. Math. Phys. 65 (2010) 17–28; doi:10.1016/S0034-4877(10)00010-8.CrossRefGoogle Scholar
Kilbas, A. A., Srivastava, H. M. and Trujillo, J. J., Theory and applications of fractional differential equations, 1st edn, Volume 204 of North-Holland Math. Stud. (Elsevier, Amsterdam, 2006); doi:10.1016/S0304-0208(06)80001-0.CrossRefGoogle Scholar
Kuznetsov, Y. A., Elements of applied bifurcation theory, 3rd edn (eds Antman, S. S., Marsden, J. E. and Sirovich, L.), Volume 112 of Appl. Math. Sci. (Springer, New York, 2004); doi:10.1007/978-1-4757-3978-7.CrossRefGoogle Scholar
Li, H. L., Zhang, L., Hu, C., Jiang, Y. L. and Teng, Z., “Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge”, J. Appl. Math. Comput. 54 (2017) 435–449; doi:10.1007/s12190-016-1017-8.CrossRefGoogle Scholar
Liu, X. and Fang, H., “Periodic pulse control of Hopf bifurcation in a fractional-order delay predator-prey model incorporating a prey refuge”, Adv. Difference Equ. 2019 (2019) 479; doi:10.1186/s13662-019-2413-9.CrossRefGoogle Scholar
Marsden, J. E. and McCracken, M., The Hopf bifurcation and its applications, Volume 19 of Appl. Math. Sci. (Springer-Verlag, New York, 1976); doi:10.1007/978-1-4612-6374-6.CrossRefGoogle Scholar
Miller, K. B. and Ross, B., An introduction to the fractional calculus and fractional differential equations (Wiley, New York, 1993); https://searchworks.stanford.edu/view/2738080.Google Scholar
Oldham, K. B. and Spanier, I., The fractional calculus: theory and applications of differentiation and integration to arbitrary order, Volume 111 of Math. Sci. Eng. (Academic Press, New York, 1974).Google Scholar
Pan, F., Cui, X., Xue, D. and Liu, L., “The Hopf bifurcation analysis in a delayed fractional SIR epidemic model”, 2018 Chinese Control and Decision Conf., Shenyang, China (IEEE Xplore, Shenyang, China, 2018), 3078–3082; doi:10.1109/CCDC.2018.8407653.Google Scholar
Podlubny, I., Fractional differential equations, Volume 198 of Math. Sci. Eng. (Academic Press, San Diego, CA, 1999); https://www.elsevier.com/books/fractional-differential-equations/podlubny/978-0-12-558840-9.Google Scholar
Sáez, E. and González-Olivares, E., “Dynamics of a predator-prey model”, SIAM J. Appl. Math. 59 (1999) 1867–1878; doi:10.1137/S0036139997318457.CrossRefGoogle Scholar
Samko, S. G., Kilbas, A. A. and Marichev, O. I., Fractional integrals and derivatives: theory and applications (Gordon and Breach Science Publishers, Yverdon,1993); https://searchworks.stanford.edu/view/2834325.Google Scholar
Wang, Z. and Wang, X., “Stability and Hopf bifurcation analysis of a fractional order epidemic model with time delay”, Math. Probl. Eng. 2018 (2018) 2308245; doi:10.1155/2018/2308245.Google Scholar
Wang, Z., Wang, X., Li, Y. and Huang, X., “Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay”, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 27 (2017) 1750209; doi:10.1142/S0218127417502091.CrossRefGoogle Scholar
Zhou, X., Wu, Y., Li, Y. and Yau, X., “Stability and Hopf bifurcation analysis on a two-neuron network with discrete and distributed delays”, Chaos Solitons Fractals 40 (2009) 1493–1505; doi:10.1016/j.chaos.2007.09.034.CrossRefGoogle Scholar