1. Introduction
In cryospheric sciences such as snow hydrology, avalanche formation/dynamics and snow climatology, daily new snow water equivalent (HNW, mm) and snow depth (HS, m) are important measurement categories. Together with wind speed, HNW is of significant practical importance for avalanche hazard estimation (Reference McClung and SchaererMcClung and Schaerer, 1993; Reference EgliEgli, 2008) and represents a key input parameter for spatially distributed snow models (e.g. Reference Lehning, Völksch, Gustafsson, Nguyen, Stähli and ZappaLehning and others, 2006; Reference Liston and ElderListon and Elder, 2006). The monitoring and modelling of water resources, represented by HS (respectively, snow water equivalent (SWE)), is the basic aim of snow hydrology (e.g. Reference Grayson and BlöschlGrayson and Blöschl, 2001; Reference Anderton, White and AlveraAnderton and others, 2002). In particular, estimates of the spatial and temporal distribution of HS (or SWE) are essential (Reference Luce, Tarboton and CooleyLuce and others, 1998; Reference SkaugenSkaugen, 2007) for water resources management (e.g. Reference Schaefli, Hingray and MusySchaefli and others, 2007) and flood prevention.
During the last decades, various expensive networks of manual and automatic point HS (and occasionally HNW) measurements have been set up in the Swiss Alps. Automatic methods have the advantage of providing data at high temporal resolution in terrain that is difficult to access. Reference Durand, Brun, Mérindol, Guyomarc’h, Lesaffre and MartinDurand and others (1993) presented a first analysis method for relevant meteorological parameters for snow models, while Reference Egli, Jonas and MeisterEgli and others (2009) investigated different methods to reveal a general feasibility benchmark in automatic estimation of HNW.
In this study, we present a virtual network (VN) to estimate HNW and HS on a regular grid (grid size 7 km) covering the entire Swiss Alps. The method is based on the HNW output data of the numerical weather prediction model (COSMO-7), developed by the Consortium for Small-Scale Modelling currently composed of the national weather services of Germany, Switzerland, Italy, Greece, Poland and Romania. The raw snow precipitation output of COSMO-7 drives a simple external accumulation/melting routine that allows HNW and HS to be computed for each gridcell. This routine does not account for individual physical processes (e.g. settling of snow cover and fresh snow). Instead, it evaluates bulk accumulation and melting rates based on COSMO-7 HNW data calibrated using observed HS data from existing snow-monitoring networks.
We believe that the VN presented here may introduce promising cost-effective options as input for spatially distributed snow hydrological models and avalanche risk management applications. If a numerical weather model and HS point measurement stations are available, a VN can be developed for other mountainous regions that are not as densely instrumented as the Swiss Alps.
2. Data
2.1. COSMO-7 model output data
A numerical weather prediction system is operated by MeteoSwiss (www.meteoswiss.ch) for a wide range of applications. This system is based on the COSMO-7 model (www.cosmo-model.org), which is a primitive equation model with non-hydrostatic, fully compressible dynamics. The prognostic variables include precipitation (separated into snow and rain) and many other meteorological parameters. COSMO-7 is used in two modes: (1) a free forecast mode, where the temporal evolution of the atmosphere is computed without any constraints other than the lateral boundary conditions from the driving model (European Centre for Medium-range Weather Forecasts, www.ecmwf.int/research), and (2) an assimilation mode to produce the best gridded representation of the atmosphere by blending available current observations with the model dynamic (the so-called data assimilation process). Note that no observed precipitation is assimilated in COSMO-7. The data assimilation process is not a simple interpolation of available observations, but instead produces a consistent state of the full atmosphere.
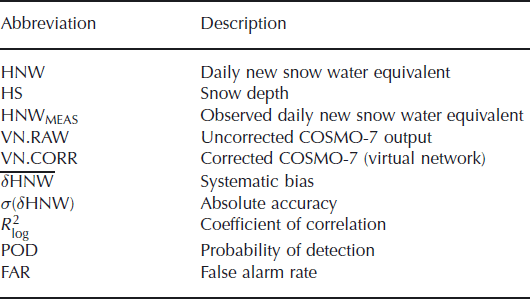
In this study we have chosen to use data from the assimilation mode of COSMO-7 between September 2005 and February 2008. For each day, snow precipitation (i.e. solid precipitation only) cumulated from 0000 UTC to 2400 UTC for the automatic reference stations (and from 0800 UTC to 0800 UTC on the following day for the manual reference stations) has been extracted from COSMO-7 and used to derive HNWVN.RAW at the surface. Introduced abbreviations are summarized in Table 1.
Table 1. Table of nomenclature
2.2. Point measurements
For this study, 141 stations spread over the entire range of the Swiss Alps (Fig. 1) were available to provide daily measurements of HS during the period September 2005 to February 2008. The sites have been carefully selected in flat open terrain, with as little wind influence as possible, to ensure regional representativeness of the HS/HNW estimation (Reference EgliEgli, 2008). In order to derive HNW from HS measurements, we used a simple parameterization proposed by Reference Egli, Jonas and MeisterEgli and others (2009):
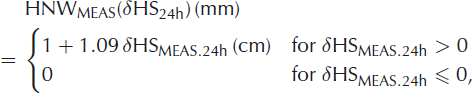
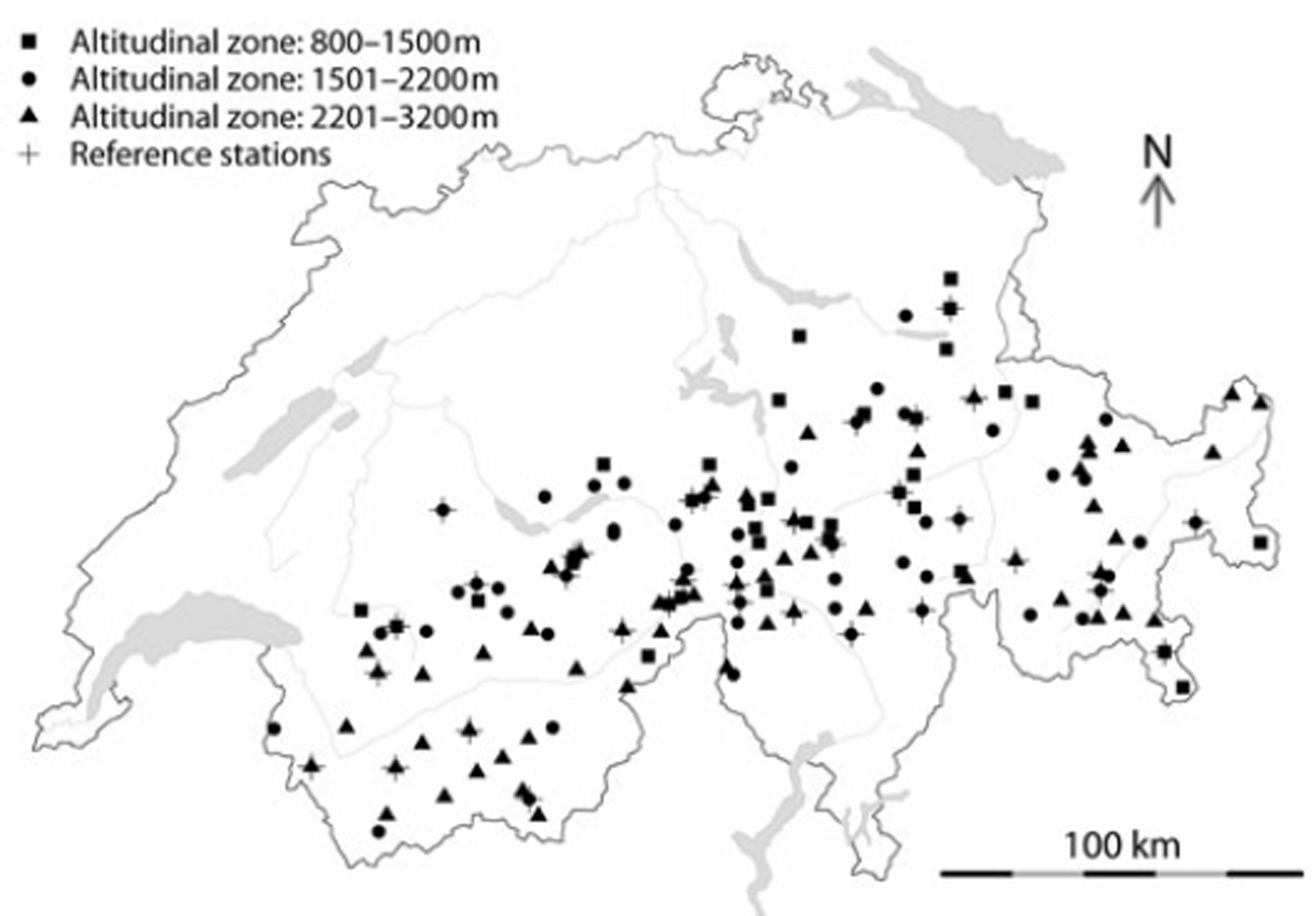
Fig. 1. Measurement stations: 141 point measurements of snow depths in the Alpine region over Switzerland. The stations are located at altitudes 800–3130 ma.s.l., where the three different elevation zones are indicated with squares, points and triangles. Reference stations are marked with a cross.
where δHSMEAS.24h denotes the 24 hour difference between an HS reading (measured here in centimetres) and the respective observations from the previous day. Possible limitations of using Equation (1) are discussed in section 4.1. Note that for automatic measurements from the network of the Intercantonal Measurement and Information System (IMIS; see Reference Rhyner and StevensRhyner and others, 2002), HS estimations were provided at 0000 h while manual HS readings (for observations, see Reference MartyMarty, 2008) were provided at around 0800 h. The values of HS were later checked for plausibility, and single missing/faulty values were corrected manually by interpolation. Finally, HNW was only calculated for the period 1 November–30 April for each season (analogous to Reference Egli, Jonas and MeisterEgli and others, 2009), while HS is considered during the entire seasons of 2005–08 if HS >0.
3. Methodology
3.1. Virtual network (VN)
HNW estimated by VN
The cumulated snow precipitation output of COSMO-7 (HNWVN.RAW) constituted the basis of the VN. Thirty-five snow stations (of 141) were set aside for adjusting HNWVN.RAW to measured HS (HNWMEAS). These stations are referred to as reference stations (Fig. 1, crosses), while the remaining 106 stations are referred to as control stations. All stations were separated into three different elevation bands (800–1500 m, 1501–2200 m and 2201–3200 m; see legend of Fig. 1).
Reference stations were selected to cover all regions and elevation bands approximately evenly, in the horizontal as well as in the vertical space. COSMO-7 mesh points were assigned to corresponding snow stations by searching the gridpoint with centre nearest to the station. The horizontal station coordinates deviated about ±2.7km on average (maximum ![]() from the centre of HNWVN.RAW, while the vertical difference between stations and respective HNWV N.RAW gridcells deviated by about ±250 m (Reference SchaubSchaub, 2007). The VN therefore covers an area of approximately 7 km × 7 km on the surface (horizontal). In comparison with the point measurement stations, a vertical distension of about 5 0 0 m is provided.
from the centre of HNWVN.RAW, while the vertical difference between stations and respective HNWV N.RAW gridcells deviated by about ±250 m (Reference SchaubSchaub, 2007). The VN therefore covers an area of approximately 7 km × 7 km on the surface (horizontal). In comparison with the point measurement stations, a vertical distension of about 5 0 0 m is provided.
The correction routine for HNWVN.RAW first identified possible outliers of HNWVN.RAW if HNWVN.RAW exceeded the maximum of HNWrMEAS at the reference stations (index r). Outliers were replaced by the maximum of HNWr MEAS for eachelevation band. Secondly, a correction matrix CorrMatr was calculated from the difference between HNWMEAS and HNWVN.RAW for each reference station and for each elevation band:
For all remaining locations (index c) of the respective elevation band, the values of the correction matrix were then interpolated by an inverse distance interpolation:
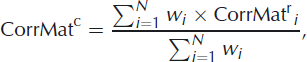
where
is the inverse distance weighting function. d represents the Euclidean metric distance operator and N is the total number of reference locations (N = 35 here). The corrected COSMO-7 HNW estimation for the control stations (HNWcVN . CORR) was then defined by:
where negative values of HNWcVN.CORR were set to zero.
HS estimation by the VN
HS is basically calculated from the summation of HNW during the accumulation period, while a simple melting procedure is used to calculate HS during the ablation period. To calculate a temporary term TEMP.HScVrN(t) for the COSMO-7 gridpoints, the values of HNWcVrN.CORR were added iteratively day by day:
Note that instead of a simple cumulation of HNWVcrN.CORR(t) for each day, this iterative procedure also allows HS to be determined for snowfall events during the melting period. However, at this point TEMP.HScVrN(t) does not indicate a real snow depth measure. In order to convert TEMP.HScVrN(t) to corresponding HS data, we employed data from the reference stations to calibrate TEMP.HScVrN(t) using a simple linear parameterization:
Again, such a parameterization was obtained for each elevation band separately. The resulting parameters of Equation (7) (slope and intercept) were subsequently used to convert TEMP.HS to HS at the control stations:
The above procedure was applied for all days (considered here as the period of accumulation) except during ablation, which is defined as all days if mean(HSrMEAS(t)) - mean(HSrMEAS(t - 4)) < 0 and mean(HSrMEAS(t)) < 0.75 × max(mean(HSr MEAS(t))). Note that this criterion does not take into account any information about the physical processes of melting (e.g. liquid water content). It approximately defines the point where the mean snow depth at the reference stations for each elevation band decreases due to melting conditions (Reference Egli and JonasEgli and Jonas, 2009). In case of melting conditions, we calculated a melting matrix from HSrMEAS(t) - HSr MEAS(t - 1) for every elevation band at the reference stations:
We calculated melt rates for all remaining locations using the inverse distance weighting method, in the same way as for Equations (3) and (4):
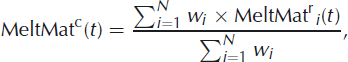
where
Finally, HS (for melting conditions) was derived for the control stations as
Note that at the very end of the winter season the reference stations would eventually melt out, preventing any melting rates from being derived. In this case, the final melting rates before meltout have been used for the interpolation. In addition, negative values of HSVN have been set to 0.
3.2. Parameters of verification
HNW verification
In order to validate the performance of HNWVN at the control stations (in the following the index c is not included) by comparing to the point measurements HNWMEAS, and to compare the results to the performance of other automatic methods, parameters of comparison were used (Reference Egli and JonasEgli and Jonas, 2009). The parameters are briefly summarized below.
-
1. Systematic bias
 :
:
-
2. The absolute accuracy σ(δHNW):
-
3.
 : The coefficient of correlation
: The coefficient of correlation  between log-transformed HNWV N and HNWMEAS.
between log-transformed HNWV N and HNWMEAS. -
4. POD and FAR: Parameters adopted from severe weather forecast theory (Reference Murphy and WinklerMurphy and Winkler, 1987) have been used to detect certain classes of snowfall events, namely the probability of detection (POD) and the false alarm rate (FAR). To calculate POD and FAR, we used contingency tables (Table 2) for four classes of HNW intensity (Snow-NoSnow: HNWMEAS ≥ 0 mm and < 1 mm; Low: HNWMEAS ≥ 1mm and < 15 mm; Medium: HNWMEAS ≥ 15 mm and < 30 mm; High: HNWMEAS ≥ 30 mm).
The POD and FAR were calculated for every class using
(15)
and
(16)
where b, c and d were derived from the contingency table (Table 2).
-
5. Ranking points: A ranking point scale for the overall assessment relative to other HNW estimation methods was tested in Reference Egli, Jonas and MeisterEgli and others (2009). For each comparative measure as described above, the best performance was rated with 7 points and the lowest performance with 0 points. The different ranking points for each parameter and class were added.
Table 2. Contingency table for the validation of the HNW estimations of the virtual network. The point measurements at the control sites HNWMEAS are observed and the estimations of the virtual network HNWVN are forecast
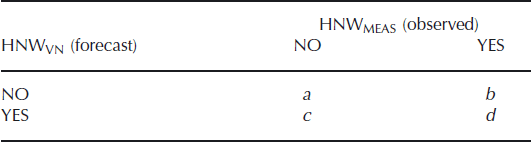
HS verification
HS data from the VN (HSVN) were validated against HSMEAS by applying the following parameters of comparison (Reference Egli and JonasEgli and Jonas, 2009), restricted to the control stations.
-
1. Systematic bias (α): The percent systematic bias α was determined by a least-squares fit to
(17)
where the standard error of α was also determined (errorα). Here, errorα is a measure of the spread of the data around the fitting line.
-
2. Absolute error (RMSE): The averaged absolute difference between HSVN and HSMEAS, the root-mean-squared error (RMSE), was included in the comparison statistics:
(18)
where i indexes one day of the analysed periods if either HSVNi > 0 or HSMEASi > 0. Since HS is investigated instead of SWE (Reference Egli, Jonas and MeisterEgli and others, 2009), a direct comparison of these studies by a ranking point score is not appropriate.
4. Results and Discussion
4.1. HNW
Results of the validation of HNWVN and HNWMEAS are listed in Table 3 and presented in Figure 2. The parameters of comparison were calculated for both HNWVN.CORR and HNWVN.RAW compared to HNWMEAS. For reference, they are listed together with corresponding results of other HNW estimation methods which were tested in Reference Egli, Jonas and MeisterEgli and others (2009). The parameters for VN.CORR and VN.RAW are averaged over all 106 control stations (Table 3: nations), where the lines below and above the end of the vertical bars in Figure 2 (as well as the numbers in brackets in Table 3) represent ±half of the standard deviation.
Table 3. Comparative statistics to assess the performance of VN relative to competing methods tested in Reference Egli, Jonas and MeisterEgli and others (2009); notation of the systematic bias ![]() the absolute accuracy (σ(5HNW)), the coefficient of correlation
the absolute accuracy (σ(5HNW)), the coefficient of correlation ![]() and the ranking point system are described in section 3.2
and the ranking point system are described in section 3.2
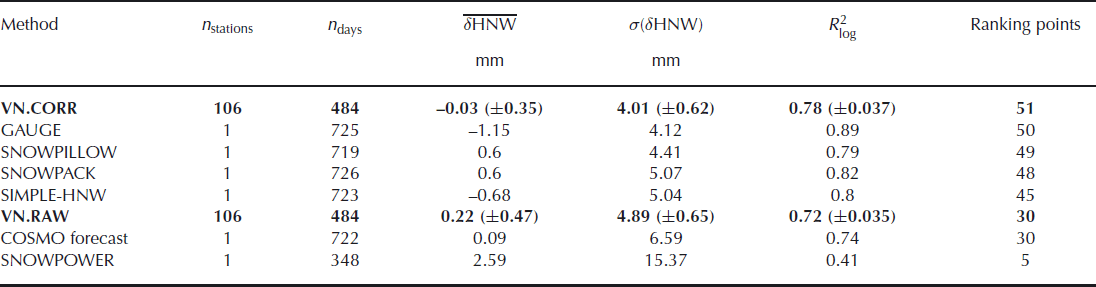
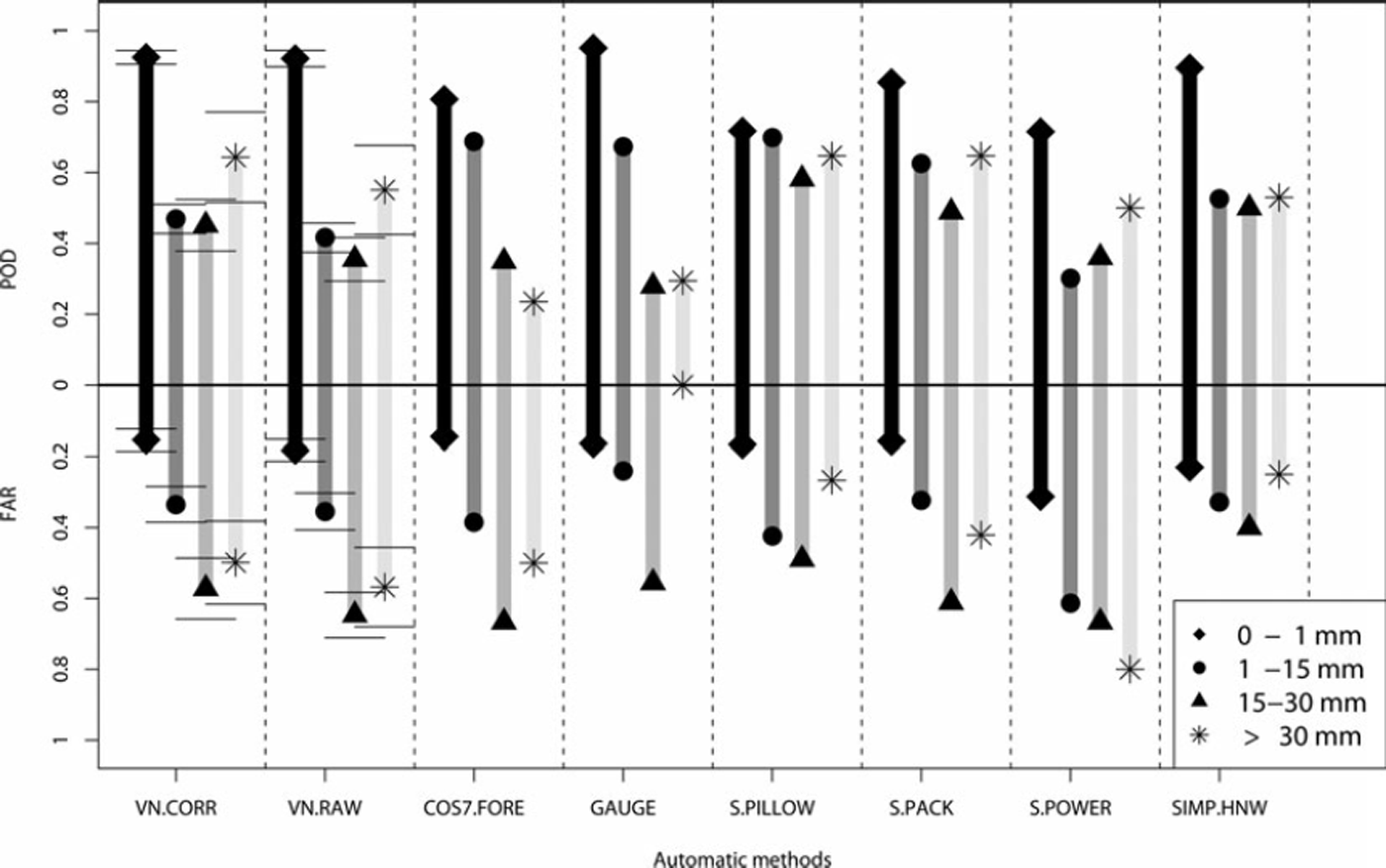
Fig. 2. POD and FAR values for the four different classes of HNW intensity (diamond, point, triangle, star). The values are listed either for single point measurements or the average of 106 control stations, where the error bars denote the deviation from the mean.
Table 3 summarizes the parameters for HNW comparison (![]() σ(δHNW) and
σ(δHNW) and ![]() ) in order of the highest ranking points. While
) in order of the highest ranking points. While ![]() indicates a general underestimation of HNW VN to HNWMEAS,
indicates a general underestimation of HNW VN to HNWMEAS, ![]() denote a statistical overestimation. The results for VN.CORR and VN.RAW reveal a systematic bias close to 0. However, the considerably large deviation around the mean values of VN.CORR and VN.RAW indicates that some stations exhibit a large under-/overestimation of HNWVN.
denote a statistical overestimation. The results for VN.CORR and VN.RAW reveal a systematic bias close to 0. However, the considerably large deviation around the mean values of VN.CORR and VN.RAW indicates that some stations exhibit a large under-/overestimation of HNWVN.
A more detailed analysis of the frequency distribution showed that the individual ![]() at each control station are approximately equally distributed around the mean value of -0.03 mm. This indicates an arbitrary character which stems from the comparison of the point measurements HNWMEAS with data representing a much larger domain of estimation for HNWVN.CORR or HNWVN.RAW. This is supported by the fact that the stations are randomly distributed in a cuboid of 7 km × 7 km by 500 m (Reference SchaubSchaub, 2007), which also explains why the deviations are generally similar for VN.CORR and VN.RAW.
at each control station are approximately equally distributed around the mean value of -0.03 mm. This indicates an arbitrary character which stems from the comparison of the point measurements HNWMEAS with data representing a much larger domain of estimation for HNWVN.CORR or HNWVN.RAW. This is supported by the fact that the stations are randomly distributed in a cuboid of 7 km × 7 km by 500 m (Reference SchaubSchaub, 2007), which also explains why the deviations are generally similar for VN.CORR and VN.RAW.
For VN.CORR, σ(δHNW) demonstrates considerably small values for the mean (σ(δHNW) = 4.01 mm) with a deviation from the mean of about ±0.62. This low absolute error σ(δHNW) implies that, in principle, HNWVN CORR can also be calibrated for each single station of the measuring network. The systematic bias of each station can therefore be reduced, resulting in a lower deviation (±) in ![]() . However, due to the comparison of a point measurement with a cuboid area, a calibration of HNWVN.CORR is not meaningful. In fact, the values of HNWVN.CORR may be considered as an average measurement of HNW over a large area, therefore representing a complementary network to the point measurements.
. However, due to the comparison of a point measurement with a cuboid area, a calibration of HNWVN.CORR is not meaningful. In fact, the values of HNWVN.CORR may be considered as an average measurement of HNW over a large area, therefore representing a complementary network to the point measurements.
Taking the performance of SNOWPACK for σ(δHNW) as a benchmark, about 82% of the 106 control stations of the VN exhibit a σ(δHNW) < 5.07mm. The absolute accuracy between HNWMEAS and HNWVN.CORR is therefore comparable to the operational SNOWPACK-HNW estimations for manual reference measurements investigated at a single location. Note that SNOWPACK calculations are in operational use for Swiss avalanche warning (Reference Rhyner and StevensRhyner and others, 2002) and provide different types of snowpack properties (Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others, 2002). However, they are restricted to the locations of the IMIS network (Reference Rhyner and StevensRhyner and others, 2002). In contrast, VN.CORR constitutes a complementary network over the entire Swiss Alps (although restricted solely to the HNW (and HS) estimation).
The POD/FAR statistics show that VN.CORR performs for all classes of intensities with better POD/FAR values than VN.RAW. Note that POD denotes the percentage of HNWMEAS, also measured by HNWVN, while FAR represents the percentage of HNWVN which are not observed by HNWMEAS. VN.CORR has similar features to the POD/FAR statistics of SNOWPACK, in particular for the two highest classes of intensity (Medium and High) and for the Snow-NoSnow class, which are the most important for avalanche risk management decisions. The good performance of VN.CORR in POD/FAR statistics with respect to the Snow-NoSnow class also implies that COSMO-7 is capable of distinguishing between snow and rain. Note that results do not deteriorate if evaluated for the three elevation bands separately (data not shown).
Furthermore, the calibration routine to derive VN.CORR implies that at the reference station HNWVN.CORR = HNWMEAS, independent of the processes leading to HNWMEAS such as combinations of solid, liquid precipitation and evaporation.
The low performance of VN.CORR in POD (0.45) and FAR (0.35) for the Low class diverges from the SNOWPACK results. In this class, VN.CORR is comparable to the performance of the SIMPLE-HNW method. This is unsurprising given that HNW are determined using SIMPLE-HNW at the control stations. This limits the potential of our approach to deal with situations in which the change in snow depth is strongly influenced by both snowfall and settling. While Equation (1) implicitly includes the effect of settling of new snow and the entire snow cover, it may become inaccurate after the first day of a multi-day snowfall event. In such situations VN.CORR therefore may not perform as well as a physical snowpack model. Note also that the difference in the time of measurements between the manual and automatic measurements (8 hours; see section 2) may lead to erroneous HNW estimates in a few cases (e.g. if a significant precipitation event occurs between 0000 and 0800 h). However, an HNW analysis of manual and automatic stations separately (data not shown) revealed very similar results with respect to POD/FAR statistics, which implies that this effect is minor.
Overall, VN.CORR demonstrates an advantage over VN.RAW. In particular, the calculation described by Equations (1–5) demonstrated the largest improvement. The method of removing the outliers has a minor impact on the results of VN.CORR. Moreover, in comparison to the other methods, VN.CORR yields the highest number of ranking points and therefore constitutes an adequate automatic estimation for HNW over the entire Swiss Alps.
4.2. HS
Figure 3 shows the temporal development of the modelled HS (HSVN, black curves) and the measured HS (HSMEAS, grey curves) during winter 2006/07 for three exemplary locations of automatic measurement stations (ELM 2, DAV 2 and DAV 3). A temporal development of HS is first displayed where HSVN describes a curve consistently below HSMEAS (ELM 2), resulting in a systematic underestimation of α = 0.65 and a mean absolute error (RMSE) of 0.42 m. Secondly, a trajectory is shown (DAV 3) where the systematic bias (α) is close to 1 and RMSE = 0.19 m, indicating a strong congruence between the curves. Finally, a station (DAV 2) is shown which describes a path constantly above HSMEAS, resulting in α = 1.54 and RMSE = 0.45 m (i.e. similar to that of ELM 2). Despite the fact that HSVN shows considerable deviation from HSMEAS for some stations, all stations generally reproduce the temporal progression qualitatively well. This is particularly true for the peaks during accumulation and the following settling (produced by Equations (7) and (8)). The same result is obtained for the ablation derived by Equations (9–12).
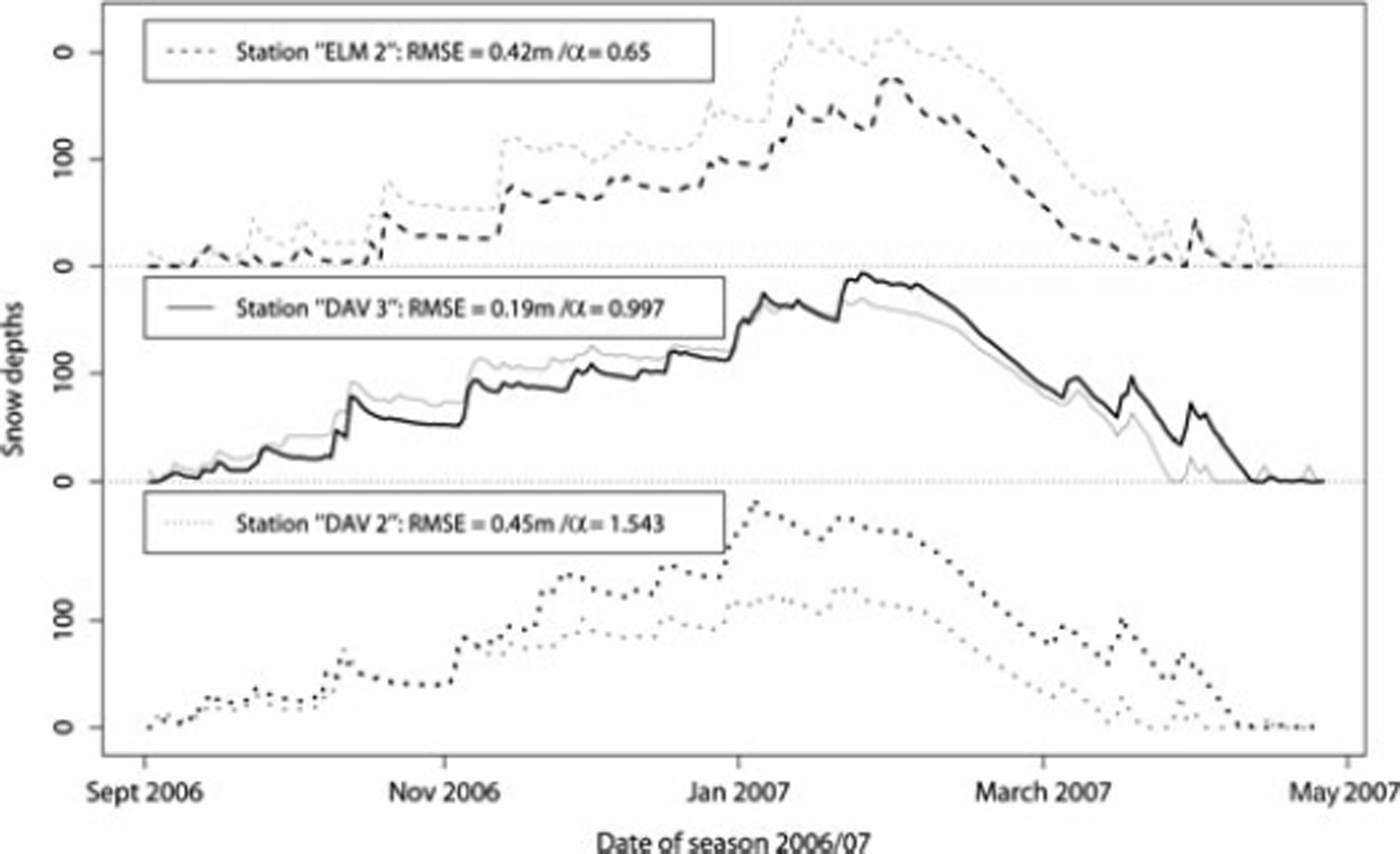
Fig. 3. The temporal development of snow depths derived by the virtual network (black curves) and the point measurements (grey curves) for three selected stations. The systematic bias (α) and the absolute error (RMSE) are indicated in the legend.
Basically, the ablation period is generated by the VN only by means of differences of HS, where the melt rate matrix (Equation (8)) actually refers to a combination of some fresh snow accumulation, settling and melting. As the peaks are attributed to snow accumulation by daily new snowfall (HNWVN.CORR), the deviation from HSMEAS stems from possible under-/overestimations of HNWVN.CORR, as discussed in section 4.1. Analogous to the results and discussion of the systematic bias of HNWVN.CORR, the specific values of a for each station are approximately equally distributed around the mean value of ![]() . Accordingly, while α is reasonably close to 1,
. Accordingly, while α is reasonably close to 1, ![]() and
and ![]() are very large (see Table 4).
are very large (see Table 4).
Table 4. The parameters of HSVN evaluation statistics (α, errorα and RMSE) as described in section 3.2 calculated either for the analysis per station averaged over 106 stations (HSVN per station), or for the analysis of HSVN averaged over all stations (average of HSVN)

4.3. Spatial analysis
Since the analysis of the single point measurements of HSVN is limited due to its random nature, an investigation of HSVN and HNWVN.CORR regarding the Swiss Alps as an entire area is also considered. First, the mean of all snow depths of point and VN estimations (![]() and
and ![]() ) and their standard deviation (CT(HSMEAS) and σ(HSVN)) are calculated. Figure 4 displays the evolution of σ(HSVN) with
) and their standard deviation (CT(HSMEAS) and σ(HSVN)) are calculated. Figure 4 displays the evolution of σ(HSVN) with ![]() (black symbols) and σ(HSMEAS) with
(black symbols) and σ(HSMEAS) with ![]() (grey symbols), where each point of the trajectory represents one day of the year 2006/07. The curves show a characteristic hysteretic dynamics as discussed in Reference Egli and JonasEgli and Jonas (2009). The trajectories of the period of accumulation (points) and ablation (triangles) are clearly separated. The quasi-linear increase of σ(HSVN) with increasing
(grey symbols), where each point of the trajectory represents one day of the year 2006/07. The curves show a characteristic hysteretic dynamics as discussed in Reference Egli and JonasEgli and Jonas (2009). The trajectories of the period of accumulation (points) and ablation (triangles) are clearly separated. The quasi-linear increase of σ(HSVN) with increasing ![]() highlights that accumulation of snow leads to an increase in the differences between sites. The path during ablation, on the other hand, is mainly attributed to the spatial distribution of melting rates in the Alpine region.
highlights that accumulation of snow leads to an increase in the differences between sites. The path during ablation, on the other hand, is mainly attributed to the spatial distribution of melting rates in the Alpine region.
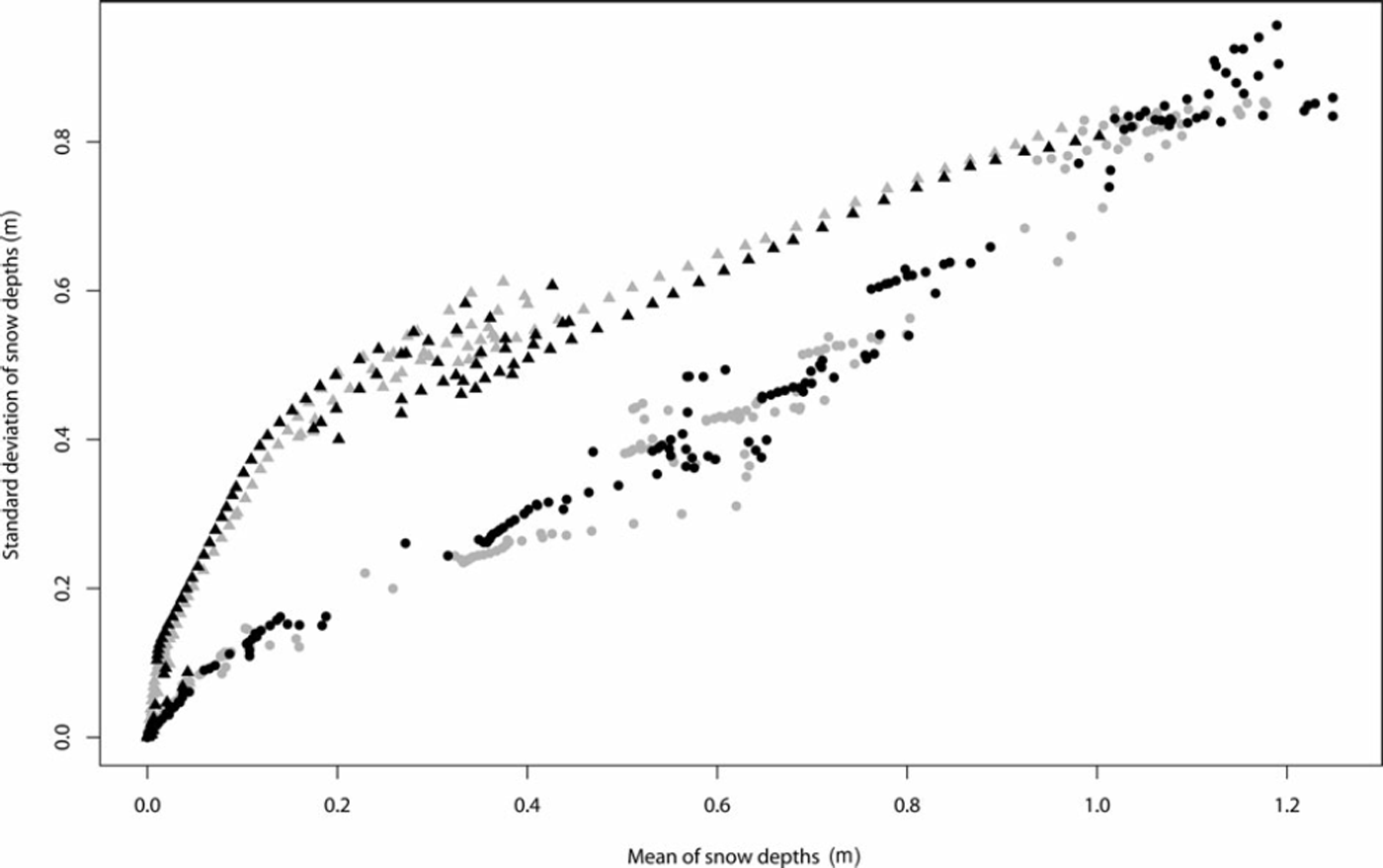
Fig. 4. The evolution of the mean snow depths (HS) and the standard deviation of snow depths ![]() derived by the virtual network (HSVN, black symbols) and the point measurements (HSMEAS, grey symbols). The trajectory during the period of accumulation is indicated by points; the trajectory during ablation is indicated by triangles.
derived by the virtual network (HSVN, black symbols) and the point measurements (HSMEAS, grey symbols). The trajectory during the period of accumulation is indicated by points; the trajectory during ablation is indicated by triangles.
It has been shown (Reference Egli and JonasEgli and Jonas, 2009) that the curves of the hysteretic dynamics are similar between years and therefore characterize the seasonal development of HS in the Swiss Alps. Figure 4 shows that both the periods of accumulation and ablation are well reproduced by HSVN when compared to HSMEAS. The seasonal characteristic of the HS development is therefore also displayed by the VN. We therefore speculate that HSVN correctly reproduces the total amount of snow depths during a season at Swiss Alpine scale. Moreover, when evaluating a, errorα and RMSE for ![]() and
and ![]() (HS is averaged day by day over all stations), the percentage bias is as small as -4% (Table 4).
(HS is averaged day by day over all stations), the percentage bias is as small as -4% (Table 4).
Furthermore, the variogram analysis of HNW (Reference EgliEgli, 2008) showed that the statistical correlation length of HNW over the entire Swiss Alps is about 50–60 km. The same correlation length was found in Reference SchaubSchaub (2007), analysing the raw HNW output of COSMO (HNWVN.RAW). This additionally supports the assumption that HNWVN reproduces the regional precipitation patterns of the Swiss Alps appropriately and can be used as an input parameter for spatially distributed snow models.
Finally, the POD statistics of point HNW measurements as a function of the distance between two measuring sites (Reference EgliEgli, 2008) showed that, for the smallest scale (5–10 km), the POD is about 60% for HNW intensities more than 30 mm (High). The same value has been derived from a comparison of HNWVN.CORR and HNWMEAS. Again, a better performance of the VN HNW estimation in the POD statistics of two point measurement stations about 7 km distant would have been astonishing, since the large area of HNWVN.CORR covers a gridcell of 7 km × 7 km. As the POD decreases rapidly with the distance from a point measurement station (Reference EgliEgli, 2008), the VN may also be applied for avalanche risk management warning for the locations between the point measurements where no HNW estimation is available.
5. Conclusion and Outlook
In this study, the HNW output of the numerical weather prediction model COSMO-7 was coupled with a simple snow accumulation/melting model in order to provide HNW/HS grids of 7 km resolution for the entire Swiss Alps. The results for the HNWVN estimation showed that, on average, its performance is comparable to the performance of different automatic point measurements. HNWVN therefore represents a complementary network for avalanche risk management applications and can also be used as input data for spatially distributed snow hydrological models where HNW is required.
This is also the case for the HS estimation by the VN, where the statistical dynamics of the mean of HS ![]() and its standard deviation (σ(HSVN)) are congruent to the measured dynamics. As a consequence, the estimations of HS by the VN over the entire Swiss Alps may be used to estimate the total amount of snow and snow water equivalent for larger catchments. At a local scale, however, a direct comparison of the point measurement to the corresponding gridcell of the VN may result in considerable deviation. This may stem from the fact that a measurement over a large area (7 km × 7 km for the VN) is compared to a single point measurement.
and its standard deviation (σ(HSVN)) are congruent to the measured dynamics. As a consequence, the estimations of HS by the VN over the entire Swiss Alps may be used to estimate the total amount of snow and snow water equivalent for larger catchments. At a local scale, however, a direct comparison of the point measurement to the corresponding gridcell of the VN may result in considerable deviation. This may stem from the fact that a measurement over a large area (7 km × 7 km for the VN) is compared to a single point measurement.
Future effort is necessary to investigate the spatial scales over which the VN is capable of providing a good performance for estimation of HNW/HS. For this purpose we will extend the application to COSMO-2, a new high-resolution version of COSMO available from February 2008 for a mesh size of 2.2 km. Additionally, the differences in the VN between the assimilation mode and the forecast mode of COSMO-2 will be investigated. Finally, the principle of the VN presented here can be applied to other regions which are less densely equipped with automatic or manual point measurement stations than the Swiss Alps. If point measurement stations and a numerical weather prediction model are available, HNW and HS can be estimated with a refined accuracy for spatially larger extended regions for avalanche-risk and water-resources management.
Acknowledgements
We thank D. Schaub and F. Schubiger for their support with the data acquisition and processing, and the external reviewer E. Brun for his constructive suggestions which helped to improve the manuscript.











