THEORY

The following continuum mixture theory for entrained snow in a turbulent atmospheric flow is based on the classical mechanics principal of conservation of mass (continuity) and conservation of momentum (momentum balance) respectively below (Decker and Brown 1983).

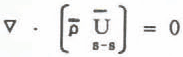
and

where

where the drift snow density ρ _s is the mean value of the mass density of snow per unit volume of mixture, C is the mean value snow velocity vector, b. is the body acceleration vector and b is the mean value air velocity vector. FT are those terms which contain time averaged products of turbulent fluctuating parameters. Where is the turbulent fluctuation of drift snow density and is the turbulent fluctuation of the snow velocity vector, D is the drag coefficient between the air and snow. D has the dimensions l/time. The snow particles in naturally occurring mixture flows are a diverse, but statistically describable distribution of sizes. The drag coefficient D could be characterized by a distribution function which would result in the mean snow particle velocity vector having a distribution of values at a given point in the mixture flow. However, in this investigation D is evaluated as a single valued function.

It is necessary to write these fluctuating turbulent parameters as a function of mean now parameters This requirement leads to the following objective constitutive assumptions for U’ and .

and

where

Where y and ϵ are vector valued functions with dimensions length and time respectively. is the mean rate of deformation tensor for the airflow, u _a, v _a and w _a are the component mean airflow velocities, “in “other words the turbulent fluctuation of the snow velocity vector and the drift snow density are proportional to the deviatone or shearing portion of the mean rate of deformation tensor of the airflow.

Then, in two space variables the terms F_ of Equation 3 expanded to the following component equations for the apparent turbulent forces. As a result of the constitutive asumption, all variables are now mean flow parameters. The mean value overscore is now neglected.

where

The apparent turbulent forces or turbulent buoyancies of Equations 7 and 8 are assumed to act such that suspension is enhanced, or stated conversely, that snow particle diffusion is less effective in those directions where gradients of the airflow are large, irregardless of the sign. To maintain this assumption, it is necessary to consider only the absolute magnitudes of the terms of Equation 9.

Additionally, if the vector valued physical constants y and e are assumed to be of the form y = y(1) and ϵ = ϵ(1) then computational tractability is greatly enhanced.

In light of these two assumptions, if the turbulent buoyancy Equations 7 and 8 are substituted into Equation 2, then by dividing through by ρ_s the non-conservative form momentum balance equation is:

Since the momentum balance Equation 10 is in non-conservative form, it is uncoupled from the continuity equation:

Equations 10 and 11 are the two dimensional turbulent equations of motion for the snow phase of the mixture flow.

Given an airflow regime, it is possible to solve the momentum balance Equation 10 for a snow particle veloicty field. By substitution of this snow particle velocity field into continuity equation 11, the drift snow density field for the mixture is solved for.

The drag coefficient, D between the snow and air phases of the mixture can be evaluated when the airflow is zero (still air) and the negatively buoyant snow particle is allowed to fall through the air at a constant rate. The momentum balance Equation 10 reduces to

or

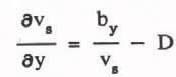
If v_s is to be a constant still air fall velocity then

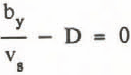
If b_y -9.81 m/sec², the gravitational potential, and the range of the still air fall velocity is -0.5 to -1.0 M/sec then D would range from 19.6 1/sec to 9.81 1/sec. For all following computations D = 13.0 1/sec.

The physical constants y and t are the constants of proportionality arising from the constitutive assumption between the turbulent fluctuations of the particle velocity vector: U’_s, the drift snow density: ρ’_s, and the de viatorie, mean rate of deformation tensor for the airflow, y and e have the dimensions length and time, respectively. There may be an intuitive desire to relate y and ε to the integral length scale and integral time scale respectively of the principal turbulent spectra of the airflow.

Principally to maintain computational stability and to fit theoretical results to observational data y and ε vary from 0.1 to 1.4 in the following computations.

COMPONENT SNOW PARTICLE VELOCITIES FOR A ONE DIMENSIONAL AIRFLOW

It is of interest to see if the theory can reproduce an inertial effect for the component snow particle velocities for a one dimensional airflow field (eg flow over a flat surface). The snow particles are introduced at the top of and allowed to fall through the boundary layer flow. Snow particles originating from the bottom of the boundary layer (eg via saltation) are not included in this solution.

The momentum balance equation reduces to:

This equation can be solved by finite difference techniques for ut and v( versus height y. b_x is zero and b is equal to the gravitational potential. The airflow profile and its gradients are given by:

where U* is the frictional velocity, k is Von Karman’s constant and y0 is the roughness height. The boundary conditions on u_s and v_s at the top (1 meter above the surface) of the solution domain are:

The results of this solution are plotted in Figure 1, showing that the theory can model an inertial effect for the snow particles by allowing the horizontal snow particle velocities to exceed those of the airflow.

Fig. 1. Component snow particle velocities and airflow velocity vs height above the surface U_a (10M) = 10 M/sec, U_a(1M) = 7.0 M/sec, y = 0.6M, ε= 0.6 sec, U* = 0.33 M/sec, K = 0.25, y_o = 0.005 M.

Also, the theory allows the snow particles to have a positive horizontal component impact velocity at the surface where the airflow velocity goes to zero.

MIXTURE FLOW AND WIND-AIDED SNOW ACCUMULATION ON THE LEE OF A MOUNTAIN SLOPE

The mixture flow and subsequent wind-aided snow accumulation on the lee of a mountain slope is a natural environment which can be theoretically modelled in two dimensions.

Wind-aided snow accumulation profiles on the immediate lee slope (30m) were collected from the summit ridge of the Bridger mountains. Access to the ridge was via Bridger Bowl Ski Area, Bozeman, Montana. The Bridger mountains are longitudinally symmetric and the longitudinal axis of the mountains is normal to the prevailing westerly winter storm winds. Wind-aided snow accumulation profiles on the lee of mountain slopes have also been measured in the Davos, Switzerland region (Fohn and Meister 1983).

It is of interest to see if the theory can reproduce a geometric approximation to these measured wind-aided snow accumulation profiles.

The theoretical approach involves:

• 1) Establishing a two dimensional geometric approximation to the mountain ridge.

• 2) Establishing a model for the airflow regime over and in the lee of the ridge.

• 3) Solve the momentum balance equation 10 for the snow particle velocity field in the lee of the ridge.

• 4) Solve the continuity equation 11 for the drift snow density field in the lee of the ridge.

• 5) Using the slope normal components of the snow particle velocities and the drift snow densities at the lee slope surface to calculate the snow accumulation flux and hence the wind-aided snow accumulation rates.

Figure 2 shows the geometry of the discretized finite difference solution domain with respect to the model ridge.

Four models for the airflow through this domain are investigated. They include two computational models for viscous fluid flow (Hirt and others 1975; Amsden and Harlow 1970), an empirical model for airflow through a half-jet (Yuu and others 1978) and data derived from a 16 mm movie of smoke-laden airflow filmed on the Bridger mountain ridge.

These airflow model data are discretized over the solution domain and the gradients of airflow are computed by central finite difference approximations.

Fig. 2. Location of the discretized solution domain in the lee of a two dimensional model mountain.

The momentum balance Equation 10 is discretized by an asymmetric finite difference approximation The subsequent system of algebraic equations is solved by a rapid update (Gauss-Seidel) iterative method for the component snow particle velocities. The non-linear velocity coefficients are treated quasi-linearly by retaining their value of the n-1 iterate during the nth iteration.

The airflow data derived from the 16 mm smoke-test movie and from one of the two computational airflow models produced algorithmically singular algebraic equation systems for the discretized momentum balance equation. Unique snow particle velocity solutions are not available from these airflow data. These airflow models had in common and differed from the half-jet airflow and remaining computational airflow model in that they contained centers of rotary flow in the discretized solution domain.

Fig. 3. Airflow velocity field and corresponding snow particle velocity field for U (freestream) = 10 M/sec, y = 1.4 M, ε= 1.4 secs.

Fig. 4. Drift snow density field corresponding to the airflow and snow particle velocity fields of Figure 3. U (freestream) = 10 M/sec, y = 1.4 M, ε - 1.4 secs.

When the component snow particle velocities resulting from the solution of the discretized momentum balance equation are substituted into the discretized continuity equation the drift snow density field is solved for. Only that snow particle velocity data that resulted from the half-jet airflow model produced reasonable (all positive) drift snow density results.

Figure 3 shows the resultant snow particle velocity field overlayed on the half-jet airflow velocity field. The boundary conditions are that component snow particle velocities are set equal to the component air velocities at the left (upstream) and top sides of the solution domain. The freestream airflow velocity of Figure 3 is 10 M/sec.

Figure 4 shows the drift snow density field corresponding to the airflow and snow particle velocity fields of Figure 3. The boundary conditions on the drift snow density field of Figure 4 are: ρ decreases logarithmically up the left boundary from a maximum of 1.65 x 10^-3 Kg/M³, to 6.5 x 10^-4 Kg/M³, along the top boundary ρ_s is set equal to 6.5 x 10^-4 Kg/M³.

In the row of solution cells adjacent to the slope surface the rate of slope normal snow flux from the mixture flow must equal the negative of the rate of wind-aided snow accumulation flux. This accumulation model contains the assumption that all snow particles which contact the snow surface in the lee of the mountain are deposited. For geometries where the airflow velocities in the accumulation zone approach zero this would be a valid assumption. However, there are mixture flows where wind-aided snow accumulation and erosion of snow particles from the surface into the flow are occurring simultaneously. In these cases, the wind-aided snow accumulation flux would be some fraction of the mixture flow flux.

Fig. 5. Theoretical wind-aided snow accumulation rates vs distance down the lee slope. U (freestream) = 10 M/sec, y = 1.4 M, e = 1.4 sec, nonwind-aid snow accumulation rates = (0, 1, 2.5) cm/hour.

Fig. 6. Theoretical wind-aided snow accumulation rates vs distance down the lee slope. U (freestream) = 5 M/sec, y = 0.1 M, E - 0.1 sec, nonwind-aided snow accumulation rates = (0, 1, 2.5) cm/hour.

Fig. 7. Theoretical and measured wind-aided total snow accumulation vs distance down the lee slope for a model storm of 4 hour duration [U (measured at ridgetop) = (9, 10, 12) m/sec, U_a (model free-stream) = 10 m/sec,] y = 1.4 M, ε = 1.4 sec, nonwindaided snow accumulation rates = 1 cm/hour.

An accumulated snow mass density of 175 Kg/M³ was assumed for all following computations. Figures 5 and 6 show the theoretical wind-aided snow accumulation rates versus distance down the lee slope for a range of drift snow density boundary conditions characterizing mixture flow without atmospheric preciptation (ground blizzard conditions) and mixture flow with two intensities of atmospheric precipitation. These boundary conditions would result in accumulation rates on any surface of 0.0, 1.0 and 2.5 cm/hour, respectively if the air was still. Figures 5 and 6 have freestream airflow velocities of 10 M/sec and 5 M/sec, respectively. At a freestream airflow velocity of 5 M/sec it is not possible to compute a stable solution that does not oversuspend or underpredict the wind-aided snow accumulation rates. The model predicts that the location of the wind-aided accumulation maximum moves closer to the ridgetop if the ridgetop drift density and/or freestream airflow velocity decreases.

Figure 7 shows the theoretical total wind-aided snow accumulation versus distance down the lee slope for a storm duration of 4 hours. The theoretical wind-aid accumulation profile results from the half-jet airflow model with a freestream velocity of 10 M/sec and the drift snow density boundary conditions characterizing moderate atmospheric precipitation. In addition, 3 measured wind-aided snow accumulation profiles from the Bridger ridge are plotted on figure 7. The storms which produced these p[rofiles had ridgetop (freestream) windspeeds of 9.5 M/sec, 11 M/sec and 12.5 M/sec. Storm duration data for the measured wind-aided accumulation profiles are not available. The model correctly predicts the location with respect to the ridgetop of the wind-aided snow accumulation maximum. However, the model over-suspends or underpredicts wind-aid snow accumulation in the region beyond the accumulation maximum.

CONCLUSIONS

Two dimensional theoretical models of turbulent atmospheric mixture flows of snow and air do produce good geometric approximations of wind-aided snow accumulation rates and profiles on the immediate lee of mountain slopes.

The computational flexibility is low for the algebraic equation systems resulting from the finite difference approximations of the equations of motion (continuity and momentum balance) for the snow phase. The computational flexibility of the theory is further restricted to those geometries where airflow models can be established either computationally, empirically of experimentally.

There is a need for additional research into solution methods other than finite difference techniques for the snow phase equations of motion.

Additional research is also needed into the physical interaction of the airflow and the particle surface leading to a description of the mechanisms which produce the apparent turbulent forces or apparent buoy anees on the snow particle. Hopefully this research would also lead to some bounds on the physical constants y and ε, the constants of proportionality between the turbulent fluctuations of the

snow particle vector U’_s, the drift snow density ρ_s and the mean deviatone rate of deformation tensor of the airflow.