1. Introduction

Thermal coupling of ice flow with the bedrock (i.e. an unde-forming substrate) occurs through two principal mechanisms: (i) the temperature field in the lithosphere couples directly with the temperature field in the ice (Reference RitzRitz, 1987); and (ii) basal topography modulates the flow of ice and in consequence both the advection of heat and the geometry of the solution domain.

In this paper, these two effects are investigated. Firstly, the transient coupling of temperature fields in ice and rock is investigated by performing a normal-mode analysis. Normal modes are the canonical way of investigating these transient effects. This has been carried out within the ice only by Reference Hanson and DickinsonHanson and Dickinson (1987). Here, the linearized thermomechanically coupled problem is considered. This investigation shows how the long time-scales associated with conduction in the lithosphere (Reference RitzRitz, 1987) couple with the flow in the ice and in particular the basal thermal boundary layer (Reference MorlandMorland, 1984). It also shows how vertical gradients in horizontal velocity lead to phasing of the temperature solution in the vertical.

Secondly, the linearized analysis is used to consider the perturbation to steady temperature fields introduced by undulations in the bedrock topography. The linearization assumes that the amplitude of basal perturbation is small compared with the thickness of the ice; the relative error in the perturbation is approximately the normalized amplitude of the bedrock perturbation. The normal-mode analysis requires far less compute time than a discretized numerical solution in all three dimensions, and thereby facilitates understanding of the sensitivity to parameter variation, in particular to the wavelength of bedrock topography.

This analysis shows how topography affects the steady temperature distribution, producing effects which are similar to non-steady effects in surface temperature, and which could therefore be interpreted as a climatically driven signal. The analysis also indicates some geomorphological consequences of temperature variations, and suggests that flow channelling as a method of increasing heating is only effective up to a point.

2. Model Formulation

We consider a base case of flow down an infinite plane. The configuration is essentially the same as considered by Reference NyeNye (1959), with the addition of evolving temperature within ice and bedrock, dependence of the viscosity on temperature, and consideration of a flow-transverse direction. Reference Clarke, Nitsan and PatersonClarke and others (1977) considered a plane flow configuration with evolving temperature in the ice and dependence of ice viscosity on the evolving temperature. On this infinite plane we have Cartesian coordinates (x;y;z), where z is “vertical” and x is in the zeroth-order flow direction. Gravity g has components (ε, 0, –1)g where ε ≪ 1. The horizontal component plays a similar role to the average surface slope in this gravity-driven flow. The thickness of the ice is given by H(x, y, t), the bed profile by z = b(x, y) and the surface by z = s(x,y,t). In this infinite plane configuration, the thickness is chosen and the flux then computed. The infinite plane configuration assumes that b; s and H are not functions of x, y or t, and these variations will be introduced by perturbing around the plane flow configuration.

We scale thickness H and elevations z, 8, b by [H] (square brackets imply a scale magnitude), vertical velocities by the accumulation rate [a], and set a horizontal velocity scale [u] and use this to construct a horizontal length scale [L] = [H][u]/[a]. Time is scaled by [t] = [H]/[a] These constructions, which are broadly consistent with the shallow-ice approximation (SIA; Reference HutterHutter, 1983), are sufficient to allow us to define viscosity/fluidity scales; this is discussed below. The ratio [H]/[L] serves as a formal expansion parameter, but in practical terms we are considering variations in basal topography which are somewhat longer than the ice thickness. Pressure p is scaled by [p] [g] [H], where p is the density of ice and g is the acceleration due to gravity. The shear stress τ_xz; τ_yz is scaled by ε[ρ][g][H] following the SIA. The ice is assumed to be below melting point for z > 0; so we do not consider temperate ice (e.g. Reference GreveGreve, 1997) within the glacier, although the pressure-melting point may be achieved at the base.

Consideration is restricted to flow of ice by internal deformation according to the viscous relationship

where e is the strain-rate tensor, τ_II is a second invariant of the deviator stress tensor τ, 9_m is the melting point of ice at zero pressure, n is the Glen index, A_c is a rate factor and R is a dimensionless function which expresses the dependence of the flow relation on scalars such as temperature and pressure. The dependence on temperature is well known in glaciology and relates to the fact that the viscosity of ice ranges by three orders of magnitude in the temperature range typical of large ice sheets (Reference PatersonPaterson, 1994). It is modelled here with a dual-Arrhenius relationship

where (c1,c₂) = (3.7 × 106, 5.4 × 1026), (E₁,E₂)= (60, 140) kJ mol_–1, and G_c = 8.314 J mol_–1 K_–1 is the universal gas constant. Here, θH is the homologous temperature, and this relationship thus introduces an implicit dependence on the pressure p which is made explicit in Equation (1). This relationship is analogous to, and produces results similar to, that proposed by Reference Hooke and B.Hooke (1981) except that it is differentiable over its whole range, and is also comparable to values recommended by Reference PatersonPaterson (1994). We ignore the pressure dependence of viscosity and sliding in this paper. It is used because it has the appropriate activation energies.

We construct

C = —2 2 A_cR; 3)

where represents the appropriate vertical average.

We use the standard (Reference HutterHutter, 1983; Reference MorlandMorland, 1984; Reference FowlerFowler, 1992) SIA. The rate factor C is scaled by The fluxes are defined as

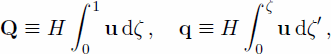
and the SIA gives the following expressions for the flux of ice:

where g_H represents the horizontal components of the gravitational body force vector. The continuity equation is

In scaled form the heat-transport equation and boundary conditions are (Reference MorlandMorland, 1984)

where u is the horizontal velocity and w is the vertical velocity. The SIA gives

which is sufficient to compute w. Here, K _i, K_r are the thermal conductivities of ice and rock, and D represents the heating due to internal dissipation given by

The quantity 9_r represents the temperature in the bedrock (with the boundary condition imposed at z = b) and there are dimensionless numbers given by

where κ is the thermal diffusivity of ice and c is the specific heat capacity of ice. Following Reference RitzRitz (1987), we also include the effect of temperature variations within the lithosphere, which is modelled as a half-space. The equation here is

and letting κ_r be the thermal diffusivity of rock, we define

In general, flow in the infinite plane implies no accumulation or melting. However, following Reference Clarke, Nitsan and PatersonClarke and others (1977) we still consider velocity fields which accommodate surface accumulation, which is essential for realistic temperature fields. In principle, these do not allow base-case flows that are shift-invariant on the infinite plane, since the ice must thicken to accommodate the increased flux. We consider wavelengths sufficiently short that the change in thickness necessary to accommodate the extra accumulation is small and representable by a linear perturbation. In consequence, this superposable solution can be subtracted out (since under the linear superposable approximation it does not couple with the perturbation we are interested in). The perturbed heat-transport equation is formally independent of (“looks identical”) whether there is surface accumulation or not. The only difference lies in the base-case temperature field, which of course has been made realistic by permitting vertical advection.

The base-case solution, which is independent of horizontal position, may be constructed by solving the steady equations

with boundary conditions

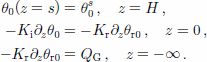
These non-linear equations can be linearized about this steady (but not necessarily dynamically stable) base solution, e.g.

The base case has constant thickness and flux, and a flat bed. The linearized fields are denoted by subscript 1, and we consider solutions for H ₁, b ₁, s ₁, θ₁ and θ_r1. Since these are defined on the infinite plane, separable solutions

are considered, where λ is the eigenvalue, i₂ = –1, the wavenumbers are given by (k_x, k_y ) and the caret indicates the Fourier coefficient. Clearly, A normalized vertical coordinate ζ = (z–b)/H is used within the ice, and henceforth 0 is considered as a function of this coordinate. For convenience, the scaling can be chosen such that H₀ = 1. Note that we do not consider evolution of the bed profile. Substitution of these into the linearized equations yields an eigenvalue problem analogous to that considered by Reference Hanson and DickinsonHanson and Dickinson (1987) but considerably more complicated. The statement of the eigenvalue problem is as follows. For the evolving ice thickness:

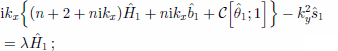
for the field equation for temperature defined in the ice:

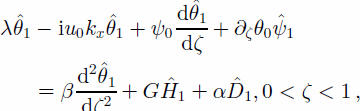
with top and bottom boundary conditions

and for the bedrock temperature equation:

The various quantities are defined as follows. Linearized forms of the fluxes are

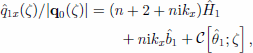
with

expressing the dependence of the rate factor on temperature. The vertical advection terms (roughly, the vertical velocities in the mapped coordinates) are

The dissipations are D₀ = 2A_cR(θ₀) (1 – ζ)n+₁ and

and γ is the lapse rate. The eigenproblem is specified by Equations (17–20c). A more extensive derivation of the eigenproblem and its solution by finite-difference discretization is given in Reference HindmarshHindmarsh (in press). Once the eigenvalues λ have been computed as a function of k_x and k_y, Equations (17–20c) can be solved with the term b̂ ₁ treated as the forcing, and ŝ₁ and 0–₁ the solution.

3. Steady Solutions of the Base Case

Steady solutions are discussed by Reference RobinRobin (1955) and Hind-marsh (1999). The parameters of the problem are the accumulation rate, the ice thickness, the geothermal heat flux, the surface temperature and the longitudinal component of gravity (roughly equivalent to the average slope of the ice surface in a glacier of finite length). Some examples of solutions are shown in Figure 1. Two of the solutions are for thermomechanically uncoupled cases (e.g. the activation energies are zero), while the other two are for thermally coupled cases, at the point where the basal temperature has just reached zero. The calculations are for ice flow by internal deformation only. A more extensive parameter study was carried out by Reference Clarke, Nitsan and PatersonClarke and others (1977).

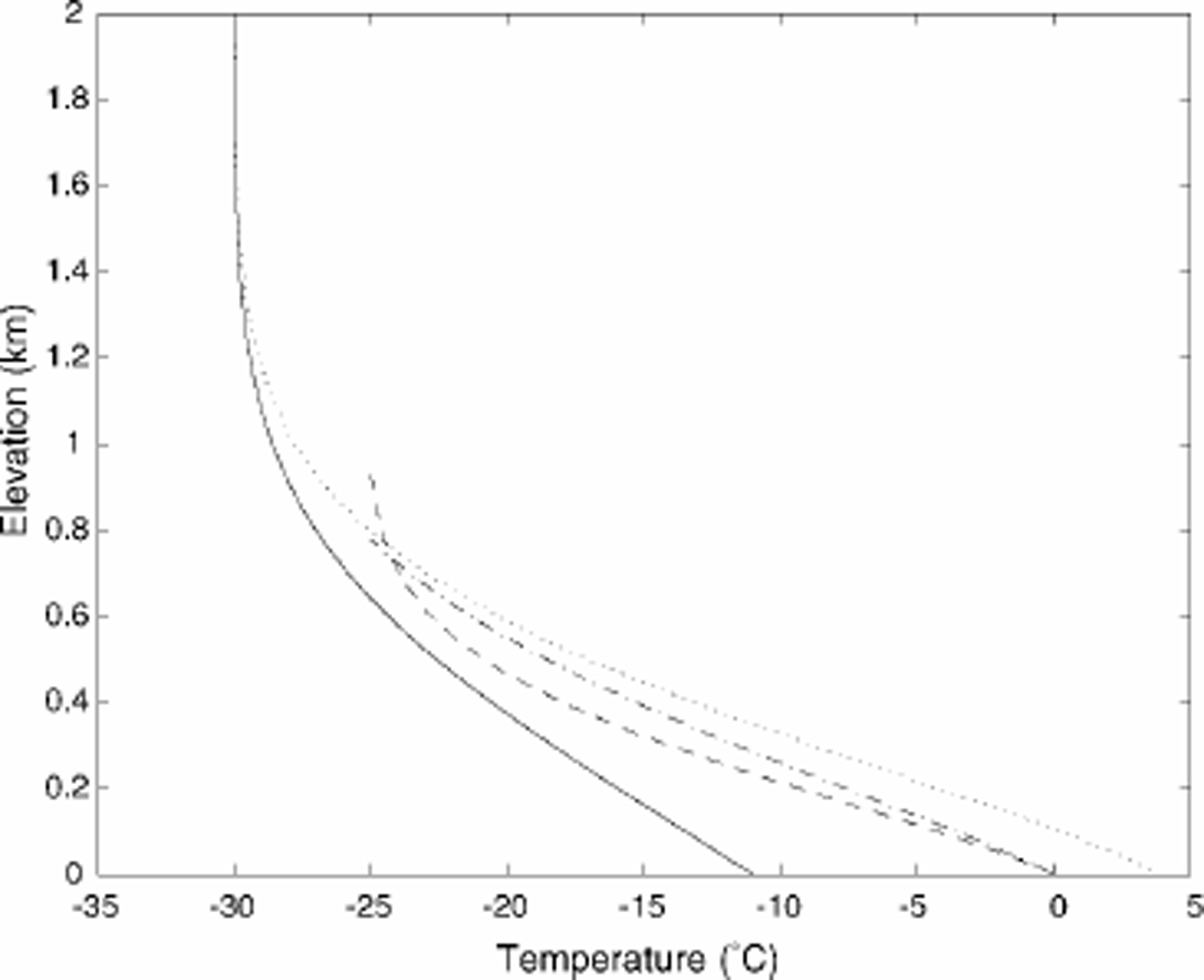
Fig. 1. Steady-temperature solutions for thermally coupled and uncoupled cases. All cases are for geothermal heat flux of 50 mWm–₂ and indicated surface temperature. The thermally uncoupled cases are for an accumulation rate of 0.3 ma_–1. Thermally coupled cases are for a slope of 0.002. Solid line is thermally uncoupled, with zero horizontal velocity; dotted line is thermally uncoupled, with horizontal velocity of 100ma_–1; dashed line is thermally coupled, with accumulation rate of 0.3m a-1 and computed surface horizontal velocity of 117ma_–1; dash-dotted line is thermally coupled, with accumulation rate of 0.1 ma_–1 and computed surface horizontal velocity of 69 ma_–1.

Allthe cases show the combined effect of advection and diffusion. The thickness of the boundary layer (where the slope reaches its largest values) is the same in each case as predicted by theory (Reference MorlandMorland, 1984). The dissipation in the case with a substantial horizontal velocity causes the increased basal temperature. In the thermally coupled cases, the parameters are the same except that the surface temperature is now –25 °C, and in one case the accumulation rate is 0.1 ma^–1. The ice is thinner than in the previous cases, which means that the Peclet number Ha/κ is smaller, and the diffusive boundary layer is thicker. The boundary layer almost fills the flow in the case where a = 0.1 m a–₁. These cases represent fairly typical computed temperature distributions.

4. Normal Modes

Here we look at the eigenvalue problem for thermally uncoupled flows, where the flows are stable. The eigenvalues represent the transient decay modes for thermal perturbations. A familiar example is conduction in a finite interval, where the eigenvectors are the trigonometric functions. In that case, the eigenfunctions have the same amplitude all over the domain, but this is not generally true of most systems, where the amplitude varies in space. Since each eigenfunction is associated by an eigenvector to a time constant, this permits identification of fast- and slow-responding areas of the system.

The work presented is an extension of work by Reference Hanson and DickinsonHanson and Dickinson (1987), considering horizontal advection and coupling with flow in the bedrock. Figure 2 shows plots of the 11 most significant eigenvectors for the two cases where (i) horizontal velocity is negligible and (ii) horizontal velocity is 100 ma–1, with the time constant (inverse eigenvalue) indicated on the axis. The eigenvectors are shown in the ice and in the top 1km of the bedrock. The bedrock domain only extends 3 km, which is deep enough to accommodate the modes excited by the forcings with period comparable to the ice-age cycles.

Fig. 2. Plots of eigenvectors for the the thermally uncoupled case (see Fig. 1 caption). Upper plot is for negligible horizontal velocity, lower for horizontal velocity of 100 m a–1. Vertical axis is absolute value of the complex eigenvector; horizontal axes are position z above base, showing all of ice and 1km of rock, and the eigenvector relaxation time constant in kyr (not to scale). The eigenvectors are part of a discrete spectrum, and the interpolating lines are purely for display purposes.

Where the horizontal flow is negligible, allthe modes have expression in the bedrock. In other words, as discussed by Reference RitzRitz (1987), the longest time-scales are associated with bedrock perturbations. The slowest mode has some expression in the base of the ice (in the conductive boundary layer), and as the relaxation times decrease, the modes have an increasing expression within the ice. All these modes are in phase with one another. The most striking feature is that the conductive boundary layer is more strongly coupled with the bedrock than with the ice in the upper part of the sheet.

Where the horizontal flow is significant, there is significantly less coupling between the thermal fields in the ice and the bedrock. There is a much clearer distinction between bedrock and ice modes, with rather limited projection of bedrock modes onto the ice. This projection increases much less slowly with mode number than the previous case, and there is an almost negligible projection of the ice modes onto the bedrock. The phasing of the eigenvectors changes with elevation, on account of the shearing motion of the ice (not shown). These results suggest differences in the way surface heating propagates into the bed which depend upon the horizontal velocity. Horizontal flow seems to uncouple the temperature fields in ice and bedrock.

5. Steady Perturbed Solutions

The linear equations can also be used to solve for the linearized steady response to forcing; in this case, the forcing is perturbations introduced by having sinusoidal variations in the bed elevation. The lapse rate was set to zero to simplify analysis of the results. The rate factor was allowed to vary with temperature in the linearized way described above.

Figure 3 shows some vertical plane contours of temperature variations arising from flow over a bump with a wavelength of around 30 km. The parameter varied is the slope (downslope component of gravity). The accumulation rate is 0.3 m a–₁, the geothermal heat flux is 50 mW m₂ and the surface temperature is –25°C. First we consider the case where the slope is 0.0001 and the horizontal flow is negligible. Then, maximum variations in temperature are co-located with maximum variations in bedrock. Above bedrock highs, the temperatures are lower, because the ice is thinner and its insulating effects are less. Above this region of colder (warmer) ice lying over the bedrock high (low), there is a region where the perturbed temperature is positive (negative). This occurs because where the ice is thinner (thicker), the Peclet number Ha/κ is less (more), diffusion is more (less) important and the warmer conductive boundary layer is thicker (thinner), warming (cooling) ice at the edge of the boundary layer. These results depend on the SIA being valid, which implies that the wavelength of the hill is somewhat greater than the thickness of the ice (Reference HutterHutter, 1983).

Fig. 3. Contour plots of temperature as afunction of position in a vertical plane parallel to the flow direction for different slopes (left to right, top to bottom 0.0001, 0.001, 0.002, 0.005, 0.01, 0.1) with indicated basal topography. Contour units are K; horizontal and vertical axes in km. The accumulation rate is 0.3 m a_–1, the geothermal heat flux is 50 mW m₂ and the surface temperature is –25°C Surface velocity for the base case is written above each plot.

Figure 3b–e show the effect of horizontal advection on phasing. The colder region is shifted downstream, and structures which look like plumes emerge. These are of course perturbations, and clearly arise from the effect basal topography has on the boundary layer. As the ice thins, the boundary layer fills the flow, and the perturbed features do likewise.

Figure 4 shows the amplitude of the basal temperature plotted as a function of x and y wavelength, and also shows the thickness and surface elevation perturbations plotted as a function of these variables. The accumulation rate is 0.3 m a–₁, the geothermal heat flux is 50 mW m₂, the slope is 0.005 and the surface temperature is –25 °C. The thickness perturbation is strong for short wavelengths, but weakens in the quadrant (L_x > 100 km, L_y > 100 km). This has consequences for the basal temperature solution; in the quadrant (L_x > 100 km, L_y < 100 km) the basal temperature perturbation reaches a plateau where it is not strongly dependent upon the bedrock wavelength, because the surface topography perturbation is not strongly dependent on either wavelength in this quadrant. In the quadrant (L_x < 100 km, L_y < 100 km) there is a strong dependence of basal temperature on the longitudinal wavelength L_x ; this is most likely to be a consequence of horizontal advection. Phasing of basal temperature (not shown) is one-signed: cold patches are always downstream ofbedrock highs, at least for these parameter values.

Fig. 4. Contour plots of absolute value of Fourier transform of perturbed quantities against wavelength in km. Upper panel: thickness; middle panel: surface elevation; lower panel: basal temperature. The accumulation rate is 0.3ma₁, thegeothermal heat flux is 50 mW m_–2, the slope is 0.005 and the surface temperature is –25-'C

Figure 5 shows a plot of perturbed basal topography and basal temperature. The accumulation rate is 03 ma^–1, the geothermal heat flux is 50 mW m₂, the slope is 0.002 and the surface temperature is –25°C. This shows the characteristic downstream offset of the cold patch, as in the plane flow case.

Fig. 5. Contour plots of basal perturbation and basal temperature perturbation against horizontal coordinates. The accumulation rate is 0.3 ma^–1, the geothermal heat flux is 50 mW m–², the slope is 0.002 and the surface temperature is –25° C.

6. Discussion and Conclusions

This paper primarily shows the complexity of thermomechanical response. The most important points are

1. There appears to be a difference in the nature of the coupling of temperature in areas of ice and bedrock in areas of slow and fast horizontal flow. This problem could usefully be analyzed in more detail than is possible in this paper.

2. Cold regions appear at the top of hills if horizontal flow is very slow. The analysis here does not extend directly to cases where cooling leads to freezing or warming to melting and sliding, but does indicate a tendency towards these states. There is some geomorphological evidence to suggest that the surfaces of hills have been frozen and protected from erosion (Reference Kleman, C. and ClarhallKleman and others, 1999), consistent with this analysis, and more generally that patches of warm and cold ice coexisted (Reference HughesHughes, 1998). However, in regions where the flow is faster, downstream areas are more likely to freeze, and this may be the cause of plucking seen on larger hills (e.g. Reference Sugden and JohnSugden and John, 1976; Reference Bennett and GlasserBennett and Glasser, 1996), since it is arguable that the stoss/lee stress differential effects often cited as a cause of plucking (Reference HalletHallet, 1996) are likely to be small on larger hills.

3. These temperature perturbations are large enough and deep enough to be misinterpretable as strong surface temperature palaeo-fluctuations (i.e. climate events). This possible problem is avoided in boreholes drilled near the divide, as is the recent practice.

4. Recent thermomechanically coupled theories of ice stream have stressed the role played by channelling in determining the onset and course of creep instabilities (Reference PaynePayne and others, 2000). The analysis here shows that the effect of channelling reaches a maximum, and does not increase as the lateral wavelength decreases. This is because of lateral diffusion of ice elevation. The interpretation of this is a bit subtle. One could argue that since channelling reaches its maximum at transverse wavelengths <100km, this is consistent with ice-stream dimensions in the sense that there should be no real tendency for ice streams markedly smaller to form. However, this starts to impinge on stability issues considered by Reference HindmarshHindmarsh (in press), who shows that there is no preferred transverse wavelength for stream formation when considering linear stability.

Thermomechanically coupled flow is a complex phenomenon. This study and some other recent studies (Reference HindmarshHindmarsh, 2001, Reference Hindmarshin press) show that real understanding is only likely to be obtained by computation and mathematical analysis.