Introduction

Surface albedo is a critical factor for the growth and melt of sea ice and its snow cover. snow surface albedo depends on both surface properties and atmospheric conditions (Reference Warren and WiscombeWarren and wiscombe, 1980). albedo decreases when snow ages and the grains become more rounded and increase in size. snow metamorphism depends on the temperature: during melting, the snow grains grow quickly and the presence of melted water between the grains further decreases the albedo. fresh snow is usually highly faceted and reflective, but also its albedo may vary greatly depending on the wetness of the grains. as the snow albedo decreases, the penetration depth of light increases, and the surface albedo is increasingly affected by the reflectivity of the deeper layers. thus, the surface albedo depends very much on the snow thickness, especially when it is <0.1m (Reference Grenfell and PerovichGrenfell and perovich, 2004). snow albedo increases with increasing solar zenith angle, especially when the grains at the surface are faceted, as the light incident at lower angles penetrates deeper into the snowpack and is more likely trapped. albedo also increases with increasing cloud cover, as the ratio of diffuse to global radiation increases and the incoming radiation flux becomes richer in the visible spectrum, for which snow albedo is higher. over sea ice, the range of variability of the surface albedo depends on the thickness of the underlying ice layer: the lower limit is given by the albedo of the melting bare ice, which decreases with decreasing ice thickness, and the upper limit is given by the albedo of fresh snow.

In the arctic ocean the onset of melt occurs in spring or summer (Reference Anderson and DrobotAnderson and drobot, 2001), while in the baltic sea snowmelt and even the total disappearance of the snowpack can occur even in mid-winter during periods of warm-air advection. the intensity of the melting and the time required to completely melt the snowpack depends on the snow thickness and the turbulent and radiative surface fluxes. since snowmelt may occur frequently during winter and spring, a detailed characterization of the evolution of albedo during the melting process is fundamental for a correct representation of the ice/snow mass and energy budgets in the baltic sea.

An accurate representation of the albedo of snow-covered sea ice in weather-prediction and climate models is a challenge. this is due to (a) the numerous factors that affect the albedo and (b) the feedback effects related to the albedo. for example, snow- and ice melt decrease the albedo, which favors further melt, while an increase in the albedo causes a decrease in the surface temperature, which favors a higher albedo. in spring, when the amount of solar radiation increases rapidly, the snow/ice albedo can change a lot in a short time. several albedo parameterizations have been developed, with various degrees of complexity (Reference Curry, J.L., D.K. and J.O.Curry and others, 2001). the simplest schemes apply two or more constant values of albedo for different surface types; other schemes add a temperature dependence when the surface approaches the melting point (Reference Ross and WalshRoss and walsh, 1987; Reference Ingram, Wilson and MitchellIngram and others, 1989). more sophisticated schemes also include the albedo dependence on snow/ice thickness (Reference Flato and BrownFlato and brown, 1996) and cloud fraction (Reference Shine and Henderson-SellersShine and henderson-sellers, 1985). the use of snow/ice thickness to parameterize albedo has the purpose of capturing the drastic albedo changes during the melt season. on the other hand, surface temperature is the most commonly available quantity that directly affects snow metamorphism and melting, and it is therefore used to parameterize the effects of snow aging on albedo. due to the positive feedback effect, a strong dependence of albedo on the surface temperature may, however, result in the growth of model errors (Reference Cheng, Vihma, Pirazzini and GranskogCheng and others, 2006).

In this paper, we analyze data on the snow/ice albedo based on measurements during a 4 week field experiment over first-year sea ice in the gulf of bothnia, baltic sea, in spring 2004. during the study period a 15 cm thick snow cover on the ice entirely melted and transformed to superimposed ice (Reference Granskog, Vihma, Pirazzini and ChengGranskog and others, 2006). the aim of this paper is to characterize in detail the sea-ice albedo changes during the melting period in the baltic sea. particular attention is paid to the daily cycle of albedo under clear skies during snowmelt, when large changes occurred in snow microphysical characteristics and snow reflectivity from morning to evening. to represent the seasonal evolution of albedo, we test some albedo parameterizations and finally propose one of them to be applied over landfast sea ice in the baltic sea and in other regions with seasonal sea ice in comparable spring or summer conditions.

Observations

Meteorological and glaciological observations were collected from 16 march to 11 april 2004 over landfast sea ice in the gulf of bothnia at a measurement site located in the vicinity of the umeå marine sciences center, sweden (63.57˚ n, 19.85˚ e; fig. 1). here we describe only measurements utilized in the present study. for a more comprehensive description of the whole dataset, we refer to Reference Granskog, Vihma, Pirazzini and ChengGranskog and others (2006).

Fig. 1. Map of the study area, with the location of the measurement site (cross), the Umeå Marine Science Center (UMSC) and the ice-edge location (solid line) in late March 2004 drawn on the basis of operational ice charts.

The radiometric station was equipped with a downward- and an upward-facing eppley psp pyranometer for measuring the upward and downward shortwave radiative fluxes (S↑ and S↓, respectively) and with a downward- and an upward-facing eppley pir pyrgeometer for measuring the upward and downward longwave radiative fluxes (L↑ and L↓, respectively). the radiation data were recorded every 1 min and averaged over 10 min. the domes of the radiation sensors were checked every morning, and, when necessary, frost or water droplets were cleaned off the domes. nevertheless, in a subsequent quality check of the measurements, some data were rejected because they were found to be affected by frost and snow deposition on the domes. since surface melting could cause some displacement of the instrument set-up, the horizontal leveling of the radiometers was checked and adjusted every morning.

We applied an empirical correction for the solar heating of the domes of pyrgeometers during daylight. it was based on the fact that when snowmelt occurred, the surface temperature could not exceed 0˚c, while the uncorrected data showed surface temperatures around +2˚c. after the correction, we estimated that the maximum relative error remaining in the longwave radiation data is 1% during surface melting, 2% during the night in freezing conditions, and 5% during daytime in freezing conditions. we calculated the surface temperature T _s from the equation:

(1)

Where σ is the stefan–boltzmann constant and ɛ is the surface emissivity (we used ɛ = 0:98). applying equation (1), the errors in the longwave fluxes result in a maximum absolute error in T _s of about 0.5˚c in near-zero temperatures, 1–1.5˚c during the night in freezing conditions, and 3˚c during daylight in freezing conditions.

The error associated with the pyranometer measurements is about 5%. the albedo was calculated from the ratio S↑/S↓ for zenith angles (z) lower than 80˚. during the field campaign, the minimum z was 54˚. for this range of z, the error due to the instrument deviation from the ideal cosine response is about ±3%, while for larger z it is much higher. measuring albedo over highly reflecting surfaces like ice and snow, most of the errors associated with the absolute accuracy of the instruments are similar for downward and upward fluxes. hence, many errors are compensated and, on the basis of the calculation of the error in instantaneous albedo measurements (Reference PirazziniPirazzini, 2004), we estimated that in our case the uncertainty in albedo is 4–7%. on cloudy days the error associated with deviation from the ideal cosine response is not present, so the total uncertainty in albedo decreases to 1–4%.

Air temperature (T _a) was recorded every 1 min at a height of 2m and further averaged over 10 min. cloud fraction and weather conditions (precipitation, visibility) were visually estimated at least every second hour during daytime.

Snow thickness (h _s) was usually measured every day with a ruler at an accuracy of about 0.2 cm. to avoid disturbances in the albedo measurements, the snow observations were made in an area away from the field of view of the downward-facing pyranometer but with characteristics similar to the surface below the radiometers. at the beginning of the campaign, the snow thickness below the radiometers (h _s≈20 cm) exceeded the mean value of the surrounding area (h _s≈15 cm). indeed, the spatial variability of snow depth was considerable: the standard deviation of the snow depth (measured at ten sites at 1 m intervals along a representative line) was 3.1 cm on 19 march, and 1.5cm on 2 april. snow density was measured every second day with a box sampler (100cm³ capacity) and a spring balance. to measure the snow density close to the surface, the uppermost 3 cm of snow were sampled, and its mean density was obtained. we estimated that the relative error in the snow density measurements, obtained from the standard deviation of the sampling at each site, is about 5–10%. ice thickness (h _i) was measured on four days (19 and 26 march, 2 and 10 april) averaging the data obtained from ten ice cores. a rough estimation of the snow grain size at the surface was made visually with the help of a ruler.

Evolution of Albedo and Atmospheric and Surface Properties

The time series of T _s, h _s and surface albedo are shown in figure 2; the resolution is 10 min for T _s and albedo, about 1 day for h _s, and about 2 hours for the occurrence of snowfall and snowdrift. it is evident from figure 2 that variations in surface albedo and h _s are strongly correlated, while no correlation seems to exist with the variations in T _s.

Fig. 2. Time series of the surface temperature (black dotted line), air temperature (gray solid line), snow thickness (triangles) and albedo (black thick line; right axis). The squares in the albedo time series mark the occurrence of snowfall or snowdrift.

The ice thickness increased during the observation period from 0.53 ±0.02m to 0.64±0.02 m, while h _s decreased from about 0.2m to 0 m, and it slightly increased again (about 0.01 m) during the light snowfall on the last day of the campaign. an analysis of the ice growth due to superimposed ice formation is presented in Reference Granskog, Vihma, Pirazzini and ChengGranskog and others (2006). during the measurement period, T _a varied from a minimum of –8.8˚c to a maximum of 8.4˚c; the variations were related to the strong diurnal cycle of solar radiation during clear or partly cloudy days, and to the advection of cold-or warm-air masses and clouds. the range of variations in T _s was smaller, between –10˚c and 0˚c (fig. 2), since T _s could not exceed the melting temperature of snow and ice.

A period of overcast sky and intermittent snowfall occurred at the beginning of the campaign, from 20 to 25 march (julian days 80–85), keeping the albedo between 0.6 and 0.8. during the first two days of snowfall, T _a was often above 0˚c, the falling snow was wet and the surface was melting; the grains were wet and soft, with 1–3mm size. the snow density of the upper 3 cm layer was 420±30 and 310±20 kgm^–3 in the morning of 20 and 21 march, respectively. because of the simultaneous snowfall and snowmelt, h _s did not change. during the rest of the snowfall period, the wind turned and cold air advected over the area, keeping T _s constantly below the melting point. on 22 and 23 march, a hard crust formed at the surface, with coarse, icy and rounded grains of 1–5mm size. the new snow that fell on 23 and 24 march was drier and with smaller grains than during the previous days, and the snow density of the upper 3 cm layer accordingly decreased to 160±10 kgm^–3. the decrease in snow grain size and density caused an increase in the albedo, which on 24 march reached the maximum observed daily mean value (0.79).

From 27 to 31 march (julian days 87–91) T _a reached maximum values, due to the occurrence of strong föhn winds downslope from the scandinavian mountain ridge. the sky was clear or partly cloudy, the air was very dry, and T _a remained above 0˚c even during two nights. in these circumstances, snowmelt and sublimation were strongly accelerated; hs decreased from 14 to 7 cm and the albedo from 0.76 to 0.52. the strong diurnal cycle of the radiation and temperature caused a diurnal cycle also in the snow metamorphism. in the morning of 27 march the sky was mostly clear, the surface was covered by a thin layer of dry snow with grains smaller than 1 mm, and the albedo was high (0.8). during the day the cloudiness increased, the snow grains at the surface became wet and bonded, the grain size increased to 1–5mm, and in the early afternoon the surface albedo dropped to 0.74. on the following day, a week of predominant clear skies began: the increase of S↓ caused a large diurnal cycle in T _a, with an alternation of melting during daylight and freezing during the night. the diurnal cycle of surface metamorphism and albedo during this clear-sky period is discussed in the following section.

The spatial variability of h _s was large, and on 4 april a few spots of bare ice appeared below the radiometers. the albedo decreased steadily until it reached values around 0.3 on 6 april, when most of the surface was snow-free. after that, the daily mean albedo decreased only a few percent per day, as the area covered by white ice progressively decreased. on 11 april, 1 cm of new snow fell, and the albedo increased again up to 0.6.

Diurnal Cycle of Surface Albedo

During clear days, night-time freezing followed by daytime melting caused a diurnal variation of albedo of 0.14, larger than the daily mean albedo differences between consecutive days. in figure 3 we present the time series of albedo during three clear days. on each of the three days a hard crust up to 1 cm thick was present at the surface in the early morning, with bonded snow grains of about 1–2mm size. during the day the crust melted, the grains became larger (2–5 mm) and loosely bonded, and in the evening the surface appeared very wet. on 28 march, h _s was about 0.12 m and albedo was higher than on 2 and 3 april, when h _s was 0.06 and 0.04 m, respectively.

Fig. 3. Diurnal cycle of albedo during three clear days. On the left are morning values and on the right afternoon values. Snow thickness (h _s) is marked for each day.

In the clear-sky mornings, albedo was proportional to z, with a coefficient of proportionality of about 0.005 deg^–1. albedo had little variation in the afternoon, and slightly increased towards the evening.

figure 4 illustrates the diurnal evolution of the snow density in the uppermost 3 cm thick snow layer during a clear and a partly clear day. on both days, the snow density was measured three times. between the two days, snowmelt occurred, the snowpack compacted and snow density increased, being higher on 30 march than on 28 march. although the error associated with the measurements is larger than the decrease in snow density during the morning hours, the same diurnal evolution was observed on 28 and 30 march and it is physically explainable: due to the melting of the crust and the percolation of the water to deeper layers, the density slightly decreased from morning to noon, but increased in the afternoon, as the snow layer compacted upon melting and the snow grains accumulated liquid water. thus, the melting process caused a slight decrease in snow density at the surface during the passage from icy crust to soft, granular snow, and a more marked increase in snow density when snow compacted and became saturated with liquid water.

Fig. 4. Variation of snow density in the uppermost 3 cm layer during a clear day (28 March) and a partly cloudy day with sun almost always visible (30 March). Vertical bars show the measurement error.

Parameterization of the Snow/ICE Albedo

Many of the sea-ice albedo parameterizations used in sea-ice, climate and weather-prediction models have set the minimum ice albedo to values ≥0.4 (Reference MaykutMaykut, 1982; Reference Ross and WalshRoss and walsh, 1987; Reference Ingram, Wilson and MitchellIngram and others, 1989), which is consistent with the observed area-averaged albedo of multiyear ice in the central arctic during summer (Reference Perovich, Grenfell, Light and HobbsPerovich and others, 2002). for the baltic sea ice cover and the arctic landfast sea ice, however, the change in albedo during the melt season is much more pronounced and albedo decreases to lower values (Reference Flato and BrownFlato and brown, 1996; Reference Ehn, Granskog, A. and A.Ehn and others, 2004; Reference Grenfell and PerovichGrenfell and perovich, 2004). this is because warmer air masses advected from the land surfaces cause stronger melting and finally the total disappearance of the ice. to find a parameterization that represents the evolution of the landfast sea-ice albedo in the baltic sea, we studied the formulas that allow the albedo to vary in the range observed during our measurement campaign. in figure 5 we compare the time series of the measured albedo with the results obtained by applying parameterizations of Reference GabisonGabison (1987; hereafter referred to as ga) and Reference Shine and Henderson-SellersShine and henderson-sellers (1985; hereafter referred to as sh).

Fig. 5. Time series of the observed albedo (thick black solid line) and that based on the parameterizations of Reference Shine and Henderson-SellersShine and Henderson-Sellers (1985; gray dotted line) and Reference GabisonGabison (1987; thin gray solid line).

In sh formulation, the albedo is defined for eight snow/ice surface types and it varies with h _s and h _i. the cloud effect on albedo is taken into account by adding 0.07 to the albedo values for cloudy skies, when albedo is >0.28. we applied the sh parameterization to calculate the albedo for the time of each cloud observation; h _s was interpolated to these times, while h _i was kept constant at 0.6 m, since its variation was too small to have any significant effect on albedo. the results obtained from sh parameterization show too small an albedo decrease during the period when h _s decreased from 0.1 m to almost 0m, and an unrealistically large step change of 0.16 when h _s became 0 m (fig. 5). the minimum albedo value over the bare ice based on sh parameterization was 0.39, while the observations indicated values around 0.30.

In ga parameterization for first-year sea ice, the albedo depends on the surface type (snow or ice), h _s, h _i and T _s. two formulas are used: (1) for non-melting conditions (T _s<–3˚c), and (2) for melting or close-to-melting conditions (T _s>–3˚c). in the case of 0.05 m≤h _i≤1m, for T _s<–3˚c the albedo of ice is a second-order polynomial in h _i, while for T _s>–3˚c the albedo decreases linearly with T _s. the snow albedo (α _s) in ga increased linearly with h _s from the albedo of the underlying ice surface (α _i) to a maximum of 0.80:

(2)

The coefficient of proportionality was given by h _s, normalized by the factor 0.05 m. a limit of this formulation is that the normalizing factor (0.05 m) must be adjusted to the maximum h _s observed at the site. otherwise, if h _s grows over the normalizing factor, the snow albedo reaches unrealistically high values, or, if h _s never reaches the value of the normalizing factor, the snow albedo never reaches 0.8. in our case, we set the normalizing factor to 0.2 m.

From figure 5 we see that the parameterization used by ga produces unrealistically large step changes in albedo, caused by the switch between two parameterizations when T _s crosses –3˚c. this suggests that, when hs is smaller than 0.1 m, the effect of h _s on albedo is larger than the effect of snow metamorphism and, accordingly, temperature.

Reference Flato and BrownFlato and brown (1996; hereafter referred to as fb) developed an albedo parameterization specifically for the landfast sea ice in the arctic. as in the case of Reference GabisonGabison (1987), their parameterization is a function of the surface type (snow, ice or open water), h _s and h _i, and utilizes two different formulas for melting (T _s=T _m) and non-melting (T _s<T _m) conditions. for T _s<T _m, fb adopted the parameterization of Reference MaykutMaykut (1982), developed for young ice in the central arctic, while for T _s = T _m, fb derived an equation based on data of arctic lake-ice albedo during the melt season (Reference Heron and M.K.Heron and woo, 1994). the parameterization reads as follows:

(3)

(4)

(5)

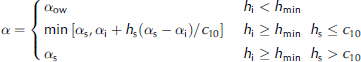
Where α is the albedo, and the subscripts s, i, mi and ow refer to snow, ice, melting ice and open water, respectively. the parameter values are c ₁₀ = 0.1 m, c ₁₁ = 0.44 m^–0.28, c ₁₂ = 0.075 m^–2, α _mi = 0.55, α _ow = 0.15 and h _min = 0.001 m.

Due to the abrupt change in albedo between equations (4) and (5), when T _s reached T _m, this parameterization produced large step changes similar to those in ga. by eliminating the temperature dependence from the parameterization and separately applying equations (4) and (5), we obtained the two curves marked with thin gray lines in figure 6.

Fig. 6. Time series of the observed albedo (thick black solid line) and that based on the parameterization of Reference Flato and BrownFlato and Brown (1996) for melting T _s (thin gray dotted line) and non-melting T _s (thin gray solid line), and the modified Flato and Brown parameterization (thick gray solid line).

While equation (4) for cold-ice albedo results in an overestimation when h _s < 0.1, equation (5) for melting-ice albedo results in a continuous underestimation, but more closely reproduces the observed trend. we decided to tune equation (5) to better fit to our data: by setting α _s = 0.75 and c ₁₂ = 0.4 m^–2, we obtained the curve marked with the thick gray solid line in figure 6. the root-mean-square error of this new parameterization is only 0.032.

Discussion and Conclusions

We analyzed the observations of broadband albedo over landfast sea ice during a period of 4 weeks in the melting season, and studied the albedo evolution in relation to the changes in surface and atmospheric properties. the complete melting of the snow layer took about 3 weeks: during this time, snowfall episodes occurred, and periods of freezing often interrupted the melting. such a snowmelt period is typical also over land areas in southern finland, with a mean duration of 15 days (Reference KuusistoKuusisto, 1984). observations from arctic coastal areas showed that the complete melting of the snowpack occurred later in the spring and took less time: in svalbard, Reference Nicolaus, Haas and BareissNicolaus and others (2003) showed that in 2002 snow melting started in late may and the 23 cm thick snow layer melted away in 5 days. analogously in northern alaska, USA, near barrow, from 2000 to 2002 the onset of melting took place between the middle and the end of may, and the snowpack had disappeared after 7–10 days (Reference Grenfell and PerovichGrenfell and perovich, 2004). the earlier melting in the bay of bothnia is due to the milder climate of the area, which is located in lower latitudes and affected by the large-scale circulation patterns that bring warm air from the atlantic ocean and central europe. during our campaign, the amount of solar radiation was much lower than in late may at 71˚n (barrow) or 79˚n (svalbard), and the alternation of daylight and night caused a diurnal cycle in snow surface characteristics that was not observed during the melting in the arctic areas, where the sun did not set.

Our results showed that when snow thickness was >0.1 m, the albedo of melting snow was between 0.65 and 0.8, depending on the age of the snow at the surface. when snow thickness was <0.1 m, a decrease in albedo due to snow metamorphism and melting caused a deeper penetration of solar radiation, and the surface albedo became increasingly affected by the darker sea-ice surface. this further accelerated the melting and the decrease in albedo. at the end of a 10 day period with snow thickness <0.1 m, the albedo of the 0.6 m thick melting ice layer had dropped to about 0.3. these results are in agreement with observations made over first-year sea ice in alaska, where snow albedo began to decrease when the snow cover became thinner than 0.1 m (Reference Grenfell and PerovichGrenfell and perovich, 2004). unlike in alaska, however, we did not observe the formation of melt ponds, probably because of the effective refreezing of the meltwater percolated deeper in the snowpack. indeed, after all the snow had melted, the sea ice was covered by a layer of superimposed ice about 14cm thick (Reference Granskog, Vihma, Pirazzini and ChengGranskog and others, 2006). during the melting process, albedo variation mostly depended on changes in snow thickness, and only very little on changes in snow or air temperature (fig. 2).

The instantaneous values of surface temperature varied between –10˚c and 0˚c, while the daily means varied between –5˚c and 0˚c. russian observations over snow thicker than 0.1 m (Reference Roesch, Gilgen, Wild and OhmuraRoesch and others, 1999), and satellite data from the central arctic (Reference Ross and WalshRoss and walsh, 1987) showed that albedo decreases roughly linearly with increasing surface temperature when approaching the melting point, although the data were scattered. the albedo dependence on surface temperature when the melting point is approached is indeed included in most parameterizations for sea-ice albedo (Reference Curry, J.L., D.K. and J.O.Curry and others, 2001), which are usually applied in coarse-resolution climate models (Reference Ingram, Wilson and MitchellIngram and others, 1989). in those parameterizations, the albedo dependence on temperature represents an attempt to simulate the lower albedo of melting snow. climatological albedo data obtained from daily or monthly means and spatially averaged data from satellites cover a range of temperatures that includes much lower values than we observed, and may smooth out rapid temperature variations. it is therefore natural that our in situ observations, covering a limited temperature range, showed a different albedo dependence on temperature (actually no correlation at all). instead, variations in snow thickness, the effect of which is masked out in climatological and spatially averaged data, became the dominant parameter controlling albedo in our observations.

Superposed on the day-to-day variation of albedo was the diurnal cycle of albedo, particularly during clear or partly cloudy days, due to the albedo dependence on the solar zenith angle and the associated metamorphism of the surface. the highest values of albedo were observed during the early morning, when the frozen surface layer of snow was covered by highly scattering small crystals, formed due to frost or rime formation during the night. as also observed by Reference Grenfell, Warren and MullenGrenfell and others (1994), a very thin layer of highly scattering crystals can strongly reduce the penetration depth of light and significantly increase the surface albedo, although the deeper snow is much less reflective. later in the morning the small crystals at the surface and the ice crust melted, and granular, wet snow appeared. the decrease in snow albedo during the morning was proportional to the solar zenith angle, with a coefficient of proportionality of about 0.005. this result falls in between the more rapid decrease observed over antarctic bare ice and the slower decrease of the antarctic dry snow (Reference PirazziniPirazzini, 2004). in the afternoon, albedo had little variation (fig. 6), reaching a value that mostly depended on the thickness of the snowpack. an analogous daily cycle of albedo has been observed previously in the antarctic (Reference LiljequistLiljequist, 1956), arctic (Reference McGuffie and Henderson-SellersMcguffie and henderson-sellers, 1985) and mid-latitudes (Reference KuusistoKuusisto, 1984). melting produced opposite effects on the density of the uppermost snow layer: in the morning density slightly decreased as the crust on the surface melted and water percolated to deeper layers, as also observed by Reference Perovich, Roesler and PegauPerovich and others (1998) during similar conditions in the arctic, while in the afternoon density increased as snow compacted and become saturated with water. the morning effect is limited to special conditions: (1) the snow layer is thick enough for meltwater to percolate down to deeper layers, and (2) the temperature of the snowpack is still below 0˚c after the freezing night, so that the snowpack is not yet wholly transformed into slush and only the uppermost few centimeters are melting.

To find a parameterization that could simulate the evolution of sea-ice albedo observed in the baltic sea, we tested on our data those parameterizations that allow an albedo variability in the range we observed. the albedo parameterization proposed by shine and henderson-sellers (1985) did not include any dependence on temperature, but produced too high albedo values when applied to our data, and caused an unrealistically large step change in albedo due to the discontinuity between two equations for snow thickness larger than or equal to 0m (fig. 4). the anomalously high albedo resulting from the shine and henderson-sellers formulation is most probably related to the fact that their equations were based on observations made in the arctic, where most of the ice is much thicker and few observational data are available for thin melting ice.

The albedo parameterizations developed by Reference GabisonGabison (1987) for first-year sea ice and by flato and brown (1996) for landfast sea ice included a temperature dependence, which caused unrealistic step changes in albedo when the temperature crossed the threshold values. the temperature values used by gabison and by flato and brown were obtained from climatological monthly means and daily means, respectively. the temperature variations were therefore much smoother than in our case, where 10 min averages were used as input in the albedo parameterizations.

Flato and brown’s parameterization for melting conditions was derived from data of arctic lake-ice albedo (Reference Heron and M.K.Heron and woo, 1994), collected from the time when the 2 m thick ice begun to melt until the time when it reached 0.5 m thickness. according to flato and brown’s parameterization, bare melting ice 0.5 m thick would have an albedo of 0.17, but this value was measured by Reference Ehn, Granskog, A. and A.Ehn and others (2004) in the baltic sea over an ice cover that was only 0.1 m thick. the low albedo values that would fit to the flato and brown parameterization could have been observed if meltwater was present on the ice surface, or in the absence of a superimposed ice layer.

We proposed a new albedo parameterization, which is only dependent on snow and ice thickness and is based on flato and brown’s parameterization for melting conditions (equations (3) and (5) with new parameter values). we are aware that this parameterization is only a crude representation of the albedo, which depends on many more variables. the strong albedo dependence on snow grain size can cause deviations from the albedo curve obtained with our parameterization, as it appears in figure 6 at the end of the time series, when a few centimeters of highly scattering fresh snow caused a sharp increase in albedo. as pointed out by Reference Grenfell, Warren and MullenGrenfell and perovich (2004), the snow thickness necessary to totally attenuate the solar radiation is about 6–7cm for fresh snow with grain radius of about 0.1 mm, and 10–12cm for metamorphosed snow with grain radii of 0.5–1 mm. nevertheless, a practical algorithm must be applied in operational sea-ice and weather-prediction models that cannot allow a sophisticated treatment of the snow microphysics. our parameterization has already been applied in a thermodynamic snow/ice model (Reference Cheng, Vihma, Pirazzini and GranskogCheng and others, 2006) and we think it is suitable for the spring season in the baltic sea, when conditions of melting and refreezing alternate.