3.1. Mechanisms

A particle on the ground can be set in motion either by air friction or by the impact of another particle which is projected into the ground. Here, the aim is to obtain the size of the potentially mobilized snow grains. Let us first look at the collisions. What we show here is that the collisions between particles and the snow cover can increase the range of size with small radius but not really with large radius. Indeed let us first suppose the “best case” of energy transmission. One particle of radius a_c arrives with a velocity u₀ If it collides elastically with a particle of the snow cover of radius a1 it gives all its energy to this particle. In this case the leaving particle will have a velocity

One can see, even in this ideal case, that to have a significant velocity the leaving particle cannot be much larger than the incoming one. In reality it seems clear that the transmission of energy is not so perfect and that not all the energy is transferred from one particle to another. So we have

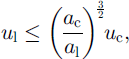
and our previous conclusion remains valid. On the other hand, the collision phenomenon gives particle sizes with no lower limit. So when we compare the results of the picking-up by collisions with the results of the picking-up by air friction, the collisions will cause us to lose the information on the lower limit. For the upper limit the collisions will have no influence. Let us now look at the range we obtain from pick-up by air friction.

3.2. Threshold velocity for particle pick-up

In order to determine the radius of the particles entrained from the snow cover by the friction of the avalanche, we use results that have been established for sediment transport by the wind and that are also used in snow transport by the wind. Here we use the results given by Reference Iversen and WhiteIversen and White (1982) (see Fig. 1). To collect their data they placed samples of material on a wind-tunnel floor and determined optically the threshold friction velocity for each of them. The particles they used were of different types and had different shapes. From their experimental results they deduced the following law:

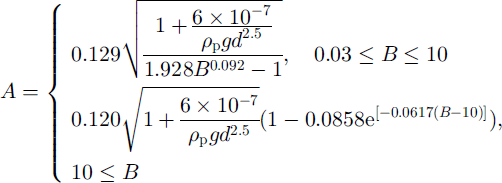
with and , where d is the diameter of a particle, A is the ratio of the threshold friction velocity to the shallow-water velocity of a density current and B is a Reynolds number.

Fig. 1. Threshold friction velocity vs diameter of the particles.

Reference Iversen and WhiteIversen and White (1982) give a lower limit (B = 0.03) but no upper limit for their law. The lower limit is outside the range of our study. Concerning a possible upper limit, we plot in Figure 1 the curve separating the regions in which Iversen and White did and did not make measurements. They say that for particles larger than 40 μm the above empirical law is generally within 5% of the experimental values. For smaller particles it is more difficult to perform the experiments, so the precision is lower; this is of no importance here since, due to the collisions, information on the lower limit is lost. As is customary in snow-transport studies, we use Iversen and White’s law here. One restriction would be that in their experiments there was no adhesion between the particles, as we can have with snow. We suppose that for powder snow such bounds do not predominate. Another restriction is that the experiments have been performed each time with one given size of particles, so that the different phenomena that can occur when there are both small and large particles are not taken into account. A further major restriction is that Iversen and White’s results were established in clean air on a horizontal floor, whereas in our case the air is loaded with particles and the ground can be inclined. From a recent study by Reference BintanjaBintanja (1998) it is inferred that the presence of particles modifies some characteristics of the boundary layer. However, not enough results could be taken into account in a modified boundary-layer model, so we use a clear-air velocity profile.

3.3. Determination of friction velocity in a powder-snow avalanche

Now that a relation between the threshold friction velocity and the diameter of the potentially mobilized particles is available, the friction velocity in a powder-snow avalanche can be determined. The avalanche studied by Reference Nishimura and ItoNishimura and Ito (1997) was a “mixed avalanche”: there was a dense part and above it a powder-snow part. We suppose that the internal structure of the powder-snow avalanche is not modified by the presence of the dense avalanche, and use the results of the measurements for the pure powder snow. The velocity of the front part of the avalanche was 40–60 ms–1. At a given point, the static pressure was measured and compared to the static pressure measured somewhere outside the influence of the flow. From this the velocity at the measuring point was measured, and for the part of the avalanche behind the front a value of 10 m s–1 was obtained. The point where the measurements were taken was located < 70 cm above the bottom of the powder-snow part; this is in the boundary layer of the powder-snow avalanche. Let us suppose that the boundary layer is of the order of 1 m thick. Later on we will see that the exact value of the size is of no importance. Thus, if z ≤ 25 cm (z ≤ 0.25,5, with = 1 m the thickness of the boundary layer), the value of the friction velocity can be directly estimated from the logarithmic law that governs the velocity in this region:

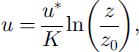
where K = 0.41 is the von Karman constant, z₀ is the roughness height and z₀ = C₀(u*f/2g, with C₀ = 0.021 (see Reference OwenOwen, 1964; Reference Rasmussen and MikkelsenRasmussen and Mikkelsen, 1991). There are, theoretically, two possible values for u* (see Fig. 2).

Fig. 2. Determination of u*.

In comparison with the values of u* found in snow transport by wind, with velocities comparable to those of avalanches, it appears that the lower value is the physically relevant one. We deduce from Figure 2 that in this region max (u*) ≈ 1 ms–¹.

In the upper region (25 cm ≤ z ≤ 70 cm) the boundary-layer profile relating velocity and height is unknown. If the measurement has been made in this region, then u(z [0; 0.25]) ≤ 10 m s^–1. So with the formula relating u and u* in the logarithmic region, one obtains u*≤1 ms^–1.Thus, here again max(u*) = 1 ms–¹.

Let us now suppose that ≠ 1 m. With the same reasoning as before, one can show that if u has been measured in the upper region, the deduced value of u* is lower than it would be if u had been measured in the logarithmic region. Because in the logarithmic region u* is decreasing with z (see Fig. 2), for any 6, for z < 0.256 the value of max(M*) remains 1 m s–¹. Thus the size of the boundary layer does not affect this estimate.

Two improvements should be made in the future: first, a better determination of u* with more field data, and second, an explanation of the presence of the particles in the boundary layer in the determination of the velocity profile u(z).

3.4. Size of the entrained particles

We can now determine the maximum range of sizes of the particles that can be picked up from the snow cover by air friction: it is [5 × 10–⁶ m; 10–² m] (see Fig. 1). To determine these values of the size (d) of the particles, formulas given by Reference Iversen and WhiteIversen and White (1982) were used (see section 3.2). The upper value of d still lies in the domain of validity of their formulas but is outside the region in which they performed the experiments. Because they did not put any upper limitation to their formula and because our range is not far from the range they studied experimentally, we think their formula is applicable for the upper value of d.

The upper limit of this interval is not changed by the collisions of particles with the snow layer, but the lower limit can be changed by the impacts (see section 3.1). Considering both air friction and collisions, the size of the mobilized particles is therefore d ≤ 10–² m.

4.1. Law relating volumetric concentration and height

To find the governing law for the volumetric concentration in the boundary layer, we use the equations of mass conservation for the mean flow of air and the equation of the mean conservation of particles

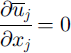
where are the components of the mean velocity of air, are the components of the mean velocity of the particles, is the mean volumetric concentration and D_t is the turbulent diffusivity that comes from the turbulent closure model: Primes signify turbulent quantities.imply that

We assume that the mean flow is steady and that the velocity and concentration profiles are independent of x. With the boundary condition that near the ground ( is the velocity perpendicular to the slope), we then have in the whole boundary layer. Boundary-layer theories Dt = Ku*z/a where σa is the Schmidt number. The Schmidt number is the ratio a_s = D_t/u_t between the diffusivity of snow particle and the eddy diffusivity of momentum. Some more advanced theories (Reference BintanjaBintanja, 1998) take into account that the suspended particles modify the turbulence of the air, so that the diffusive coefficient D_t is modified:

where R is the flux “snowdrift” Richardson number, ρ_p is the density of particles, p is the density of air and g is the gravitational acceleration. The orders of magnitude of the different quantities are the following: , and as = 0.5 (see section 4.2). From this we can deduce that [1 +AR]≈ 1. So within the precision of our study, this modification need not be taken into account.

To solve the second differential equation, we assume that the particle volumetric concentration and its gradient vanish infinitely far from the boundary layer

The steadiness of the flow, the independence of the concentration profiles of x and the fact that imply, using Equation (6),

where a is the angle of the slope and From this and with the boundary conditions (see Equation (8)) we deduce

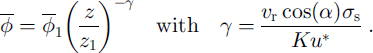
is the volumetric concentration at z = z₁. Let z₁ be the roughness height, so that is the volumetric concentration of the particles near the ground, i.e. the volumetric concentration of the mobilized particles. v_r is a function of the size of the particles, so the variation in the boundary layer of the volumetric concentration will not be the same for different types of particles.

4.2. Presence of the particles

To know which particles effectively reach the top of the boundary layer, we study the ratio between the number of particles at the top of the boundary layer and the number near the ground; to this end we look at the repartition with the radius a defined as

It defines the concentration of particles by which the body of the avalanche is fed from the boundary layer. To determine γd, the relative velocity must be given as a function of a. We assimilate it with the sedimentation velocity, which is obtained from the Lagrangian equilibrium state where the gravity force is balanced by the drag force. From this equilibrium we obtain

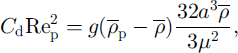
where C_d is the drag coefficient and Rep = 2aρv_Y/μ is the particle Reynolds number. For spherical particles, which we assume the snow particles in the flow to be, the drag coefficient is as follows (see Reference Niño and GarciaNiño and Garcia, 1994):

Another parameter is the Schmidt number (σrs) which takes different values in different configurations. Reference Householder and GoldschmidtHouseholder and Goldschmidt (1969) found that for particles denser than the ambient fluid, the Schmidt number is < 1. Reference Naaim and MartinezNaaim and Martinez (1995) performed wind-tunnel experiments with PVC particles and found a Schmidt number of 0.5–0.6. We performed calculations for both σr_s = 1 and <σ_s = 0.5. The last parameter to fix is u*. As before, because we look for the larger range of particle sizes, we take u* = lm s–1. The results are shown in Figure 3. To demonstrate that the dependences on σr_s and on the thickness of the boundary layer are weak, we plotted the curves for σr_s = 1 and σr_s = 0.5, and 6 = 50 cm and 6 = 5 m. In all cases the size of the particles, which are still present in significant numbers at the top of the boundary layer, is <2 × 10–4 m.

Fig. 3. Repartition for a_s = 1, σ_s = 0.5, b = 50 cm and 6 = 5m.