1. Introduction
Ever since a handful of extremely influential articles (Hughes, 1973; Weertman, 1974; Thomas and Bentley. 1978) were published in the 1970s, marine ice sheets have been widely regarded as being unstable. Stability is an elusive concept and it is not surprising that this instability has been discussed in rather different terms by a number of different authors. What all of these analyses have in common is the absence of a discussion of the stability of marine ice sheets in terms of two of the most widely used notions of stability, asymptotic stability and Lyapunov stability (e.g. Hale and Koçak, 1991).
In this paper we shall consider the limited but important technical objective of the linear stability and evolution of marine ice sheets which do not contain any ice streams and are modelled as being decoupled from their ice shelves. We do this by considering a normal-mode stability analysis, which informs about the linear stability of marine ice sheets.
A marine ice-sheet system consists of two or three parts, a grounded ice sheet, floating ice shelves and perhaps an intervening ice stream. In the grounded sheet, shear-flow dominates, while in the floating shelf, the flow is extensive. In the sheet, the vertical shear-stress gradient balances the longitudinal vertical normal-stress gradient, while in the ice-shelf shear-stress gradients and longitudinal deviatoric stresses gradients balance the vertical normal-stress gradient. Clearly, there must be an intermediate zone in the grounded ice where longitudinal stresses play an important role.
We shall follow the view of Hindmarsh (1993), who regarded the transition zone as being of such limited extent in the direction of flow as to be unable to affect the flows in the ice sheet and in the ice shelf, in much the same way as the anomalous flows in the divide are not believed to affect the large-scale flow. The transition zone is thus regarded as a passive boundary layer. Numerical calculations (Herterich, 1987; Lestringant, 1994) and a related analytical solution (Barcilon and MacAyeal, 1993) support this view. Hindmarsh (1993) reviewed opposing views.
Those who argued that the transition zone is a passive boundary layer are logically forced into the position that the ice-shelf flow does not affect the ice-sheet flow (apart from eases where the ice shelf grounds) and that sensible predictions can be made about marine ice sheets without computing flows in any associated ice shell. This is equally true of confined and unconfined ice sheets, the point being (Hindmarsh, 1993) that back-pressure tenus are of the same order of magnitude as the longitudinal stress-gradient terms. These do not affect grounded ice-sheet flow at leading order.
Indeed, it is possible to construct a grounding-line advance formula based on kinematics (Salamatin, 1989; Hindmarsh, 1993) which does not require any information from an ice shelf. Such a formula respects mass conservation by stating that what leaves the ice sheet is determined by the flow in the ice sheet, using the usual shear-stress formula, up to a zone a few ice-sheet thicknesses upstream of the grounding line. This is exactly the same as assuming that one can safely describe the large-scale flow of grounded ice sheets ignoring the anomalous mechanics near the margin, and indeed the appropriate margin-advance formula (e.g. Hindmarsh and others, 1987) is based on the same conservation/kinematical principles as the marine ice-sheet grounding-line advance formula.
While it is common in glaciology to assert that longitudinal stresses must be modelled at the grounding line, there has been no rigorous discussion of why, if this is so, it is not also equally necessary at land-based margins. The approach in this paper is entirely consistent with the approach adopted by the author anal co-workers in previous moving-grid modelling of land-based ice sheets, both in its application of the margin/grounding-line advance formula and in assuming that the anomalous mechanics near the margin and grounding line form a passive boundary layer, the mechanics of which do not affect the large-scale mechanics.
Even if ignoring ice streams is not a good model of large marine ice sheets, one may note that ice rises are simply mini-marine ice sheets. The crevassing between ice shelf and grounded ice is an indication of a lack of coupling; certainly, there is no basis for assuming that stress fields are differentiable across these zones, which asks t the question of how ice shelves are then supposed to influence the mechanics of slowly moving grounded ice. The only reason for supposing that increased longitudinal stresses in the transition zone should destabilize the grounding line is if one can show that no other stabilizing mechanisms exist. A stabilizing mechanism based on kinematics is outlined in section 3.
Ice rises are not drained by ice streams, meaning that they are describable and presumably modellable in the simple terms described above. For this reason alone, modelling marine ice sheets without ice stream or ice shelf is a valid and relevant scientific problem, and is a natural first step to understanding the dynamics of more complex ice sheets. It is an obvious question to ask whether the large-scale flow of decoupled marine ice sheets is stable or unstable. This paper explicitly shows that the dynamical characteristics of the governing equation and the corresponding finite-difference scheme are the same. Such demonstrations are surely a prerequisite to claiming that a given model informs at all about the stability of marine ice sheets.
When one asks the next question, which is “Can we characterize the asymptotic or Lyapunov stability of marine ice sheets”, one runs into major difficulties, Hindmarsh (1993) has shown that an infinity of equilibria exists and has argued that this implied neutral equilibrium or metastability. Tints, rather than lying on a point or points in phase space, the set of equilibria are non-denumerable and lie on a line in phase space. In this paper, we term the line in phase space, where the ice sheet is in neutral equilibrium, the “equilibrium manifold” (to avoid calling it the equilibrium line).
The question then arises of whether this metastability property is structurally stable, that is stable tinder small perturbation to the model equations, and also flow the issue of structural stability extends to the iterated maps used to solve discretized representation of the partial differential equations describing the evolution of uncoupled marine ice sheets. This issue of structural stability is the reason why it is much more important, in the case of marine ice sheets, to demonstrate the dynamical equivalence of governing equations and a finite-difference marching scheme. The dynamics of grounded ice sheets are structurally stable except at bifurcation points, meaning that dynamical equivalence is far easier to obtain and is not really an issue.
Hindmarsh (1993) demonstrated some of the consequences of Structural instability by comparing a semi-analytical ice-sheet model based on the similarity solution for ice-sheet spreading (Halfar, 1981) and a numerical finite-difference scheme. The semi-analytical method produced valid solutions to the ice-sheet profile-evolution equation used by Mahaffey (1976) and showed metastability. This model had a reduced number of degrees of freedom (only certain spatial patterns of accumulation could be accommodated). A numerical finite-difference model (which could accept as many-degrees of freedom of forcing as there were grid points) showed different qualitative behaviour with the ice sheet growing unstably. The rate of unstable growth was strongly dependent on the spatial discretization interval, suggesting numerical effects were yielding a false qualitative dynamics. Thus, the iterated map was not structurally stable to discretization error and led to spurious unstable behaviour which manifested itself at long wavelengths rather than the short wavelengths typically associated with numerical instability.
The implication of this, taken with the argument that ice shelves were not a necessary part of the calculation, was that other marine ice-sheet models were also possibly-generating a spurious qualitative dynamics through numerical error, and that the different qualitative behaviour reported by different modellers could be a consequence of differences in the numerical schemes. Also implicit in this is that basic response of marine ice sheets (or at least ice rises) to forcing is simply not known.
It is quite easy to find examples of numerical schemes which give spurious dynamics - for example, a forward Euler integration scheme on Newton’s equations for the motion of a body orbiting under gravitational attraction will not produce a stable solution. This is not too serious a problem for systems whose dynamics are reasonably well understood analytically. Such an understanding is not yet present for marine ice sheets.
The purpose of this paper is to carry out a linear stability analysis of the ice-sheet equation around a steady solution and to construct a numerical scheme which has the same stability properties, at least in the vicinity of the equilibrium manifold.
2. Stability and Metastability
A dynamical system is characterized by an evolution equation of the form
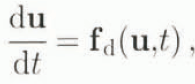
while an iterated map is characterized by an equation of the form
where u is a vector, It can readily be seen that one example of an iterated map is a finite-difference or finite-element marching scheme. The asymptotic stability of a dynamical system or an iterated map is usually defined in terms of neighbouring trajectories in phase space which are close at one point in lime moving towards each other with an exponential decay, while unstable systems have neighbouring points which move apart. The less restrictive Lyapunov stability simply requires that on average trajectories do not diverge. Local linear stability for all these cases can then be analysed by first computing a Jacobian matrix, i.e.
The solutions for small perturbations u′ are
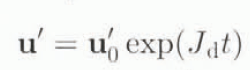
for the dynamical system and u′ k is
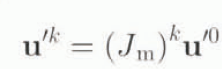
for the iterated map. The stability of these linearized systems can then be assessed by computing the eigenvalues of the Jacobian matrices using standard techniques (e.g. Wilkinson, 1965).
For a dynamical system, Lyapunov stability occurs when none of the eigenvalues has positive real parts, while asymptotic stability requires that all the eigenvalues have negative real parts (Hale and Koçak, 1991). Instability occurs when one or more of the eigenvalues have positive real part. For an iterated map, the conditions relate to the modulus of the eigenvalue - instability occurs if any of the eigenvalues have (complex) modulus greater than 1, asymptotic Stability if all the eigenvalues have modulus less than 1.
Non-linear systems have Jacobians which depend upon the state vector u and, in general, we expect the stability characteristics to change with u. Points in phase space where the stability characteristics change are called bifurcation points and for our purposes we shall consider them as points in phase space having eigenvalues with zero real parts.
Metastability is loosely considered to occur when several equilibrium points exist but true metastability occurs when there is a manifold of non-zero dimension (i.e. a smooth object in phase space which is bigger than a point, in this case a line) which represents equilibrium configurations in phase space. We shall see that there must exist a zero eigenvalue with an associated eigenvector which corresponds to movement along the equilibrium manifold.
Iterated maps can possess equivalent manifolds where the complex modulus of the eigenvalue has magnitude exactly 1. Indeed, this is precisely the point of the paper; can we design an iterated map which is a consistent finite-difference representation of a related dynamical system, both of which have equilibrium manifolds? As pointed out in the introduction, no-one modelling marine ice sheets hitherto has carried out the basic technical requirement of proving the dynamical consistency of the numerical scheme and governing equations. In consequence, the quoted results simply tell us about the stability characteristics of their marching schemes. These may be the same as the dynamical system; whether this is so or not is the main issue considered in this paper.
3. Boundary conditions at the grounding line
Let ns consider the force balance across a narrow grounding zone, which requires that two boundary conditions be satisfied, one prescribing the tangential traction and the other the normal traction. We also need a kinematical condition, which here describes the speed of translation of the grounding line.
Flotation occurs when the normal traction on the base of the glacier equals the water pressure. Under reduced model assumptions for both ice sheet and ice shelf (e.g. Morland, 1984, 1987), the upwards tangential traction is ignored. In this case, the normal traction is glaciostatic, so flotation occurs when
where f is the water depth, H is the thickness of the ice sheet, g is the acceleration clue to gravity and ρ i , ρ w are the densities of ice and water, respectively. The co-ordinate system is illustrated in Figure 1. Numerical calculations (Lestringant, 1994) indicate that the deviation from hydrostatic conditions is small.
Fig. 1. Illustrating the coordinate system used. The notional ice shelf indicates that the presence or absence of an ice shelf does not affect this model of grounded ice.
The normal force F x from the ice sheet acting on the transition zone is
while the force from the ice shelf is
Here, σ xx represents the longitudinal deviatoric stress, s the ice-surface elevation, b the ice-base elevation, z is the vertical coordinate, x is the horizontal coordinate and the superscripts “sheet” and “shelf” represent evaluations sufficiently far upstream and downstream of the transition zone for the values of the longitudinal stress to be computable using the appropriate standard reduced models. These domains of validity are expected to occur a few ice-sheet thicknesses from the grounding line, both on the basis of order-of-magnitude argument and from looking at numerical solutions (Herterich, 1987; Lestringant, 1994).
The difference between these two forces is 2Η([inequation]) and force balance in the transition zone is satisfied by an increased tangential basal traction since ice-shelf average longitudinal stresses are in general larger than those in ice sheets. This integral formulation does not specify uniquely bow the longitudinal stresses and tangential traction increase in the transition zone, and increases in both stresses will lead to increased velocity, but the profile can still be steady, albeit with an increased slope.
Those who argue that the transition zone is unstable in effect say that the term Η∂ x ū becomes very large (which may be true) and that in consequence ∂ t H < 0, leading to grounding-line retreat, and that this effect is counteracted by buttressing from the ice shelf, which acts to reduce the longitudinal stresses. However, buttressing is not the only stabilizing mechanism. Consider the continuity relation
where ū is the average velocity in the ice. Any thinning will immediately cause ∂ x H to become more negative and the term ū∂ x H now acts in such a fashion such as to stabilize the system. This stabilization mechanism works even if thinning leads to enhanced sliding velocities as a result of a decrease in effective pressure or the increased shear stress. There may be an instability arising from the sliding law (Budd and others, 1984) but it is not a necessary consequence of the properties of the grounding line. In short, statements arguing the instability of the transition zone are not well borne out.
If the transition zone is stable and is of the order of a few ice-sheet thicknesses in length, the discharge and discharge gradient will not increase a great deal from the downstream end of the zone of validity of the reduced model to the ice front. This is a consequence of continuity and means that we can compute the discharge from the slope and thickness at the grounding line as though the shallow-ice approximation held good. This is equivalent to the procedure adopted by all ice-sheet modellers at land-based glacier margins and is valid because the moving-boundary condition in both cases is consistent with the shallow approximation and does not therefore require the imposition of further boundary conditions. This principle has been discussed further by Fowler (1992).
4. The ice-sheet equation in a stretched grid
The governing equation we are considering is the ice-sheet equation
where H(x, t) is the thickness of the ice sheet, s(x, t) is the upper surface and a is the surface mass-balance exchange. We define a mass flux
The horizontal, vertical and time coordinates are (x, z, f). This equation describes the evolution of ice-sheet thickness when the flow mechanism is either internal deformation according to some non-linearly viscous flow law or sliding according to some Weertman-type law. We can include both effects but it would make the present analysis unnecessarily cumbersome.
Thus, the quantity C is directly related to either a rate factor A d used in the viscous relationship
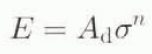
where E is a second invariant of the deformation rate and σ is a second invariant of the deviator stress (Glen, 1955) or comes from a sliding relation of the form
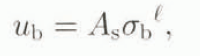
where σ b, is the basal shear stress. We construct the following quantities for use in the general evolution equation
The derivation of the evolution Equation (2) using the shallow-ice approximation is standard (Hutter, 1983; Morland, 1984; Fowler, 1992) and what amounts to essentially the same formulation has also been sketched by (Hindmarsh (unpublished).
Let us write down the moving-boundary condition for a marine ice sheet. The flotation condition is
where f is the depth of the water at the grounding line and if we write this in total differential form, following the moving grounding line,
which is
and which yields an expression for the grounding-line migration rate G r ,
and using the continuity equation ∂ t H + ∂ x q = a we may write
where all the quantities on the righthand side are evaluated at the grounding line. If we ignore self-gravitating effects (which also affect the ice sheet) and take sea level to be constant in space, we may write ∂ x f = −∂ x b. This grounding-line advance formula was given with incorrect sign on the bed-profile term by Hindmarsh (1993). Salamatin (1989) constructed a similar (correct) equation but introduced an unnecessary (for the purposes of constructing a simple model) extra assumption of sliding in the transition zone. This total differential construction is equivalent to procedures for computing the migration velocity of margins in land-based ice sheets (Hindmarsh and others, 1987).
A crucial part of the procedure of assessing the stability of iterated maps is the computation of the Jacobian, which involves differentiation. Fixed-grid ice-sheet models must have some rule for determining which grids are occupied by ice and which are not, which are essential parts of the time-stepping procedure, The use of these rules within a computational algorithm would seem to involve, in general, the use of conditional execution (“if” statements). These cannot be differentiated in any meaningful way, implying that the simplest way to carry out a stability analysis is to use a moving-grid algorithm.
Thus, following for example Hindmarsh and others (1987), we define a normalized horizontal coordinate ξ = x/S, where S is the semi-span of the ice sheet and we consider the case symmetric about the divide at x = ξ = 0 only. Thus, G r — Ṡ. The time coordinate corresponding to t is denoted τ, and we choose τ = t.
Following Hindmarsh and others (1087), the evolution equation in stretched grid form may be written
where, in our stretched coordinates the grounding-line migration formula becomes
where ρ wi = ρ w/ρ i and ∂ ξ .J = ∂ ξ .H − ρ wi ∂ ξ . f.
5. Normal-mode stability analyses
Linearizations of non-linear partial differential equations and computation of their normal modes are commonly used in fluid dynamics, in order to assess the linear stability of the system (Pedlosky, 1986; Tritton, 1988). The purpose of the analysis is to determine whether a small perturbation grows. The Lax Equivalence Theorem requires that a necessary condition for a finite-difference (or finite-element) scheme to be convergent to a given partial differential equation as the discretization interval tends to zero is that the finite-difference scheme, when viewed as an iterative map, should have the same stability properties as the differential equation. How these stability properties are compared has already been discussed in section 2. The stability of the governing equations and of a particular numerical scheme (not necessarily she most efficient one) are examined in the following sub-sections. It is shown that the numerical scheme has the same stability properties as the governing equation on the equilibrium manifold provided time steps are kept short enough. This is the first time that a numerical model of a marine ice sheet has been shown to bear this relation to the governing equations.
5.1. Perturbed marine ice-sheet equations
Let us expand the relevant variables as a series in a small parameter μ such that
where μ ≪ 1. We shall perturb around configurations where S 0 and H 0 represent steady solutions. As discussed above and in Hindmarsh (1993), we expect the zeroth order solution to be non-unique, as we can choose any divide thickness H 0 and integrate the profile away from the divide until the flotation condition is satisfied.
Substitution of these expansions into the ice-sheet equation yields to O(μ) two equations: at zeroth order
and at first order
Assuming symmetry around the divide and introducing the notation
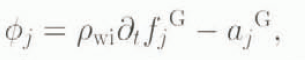
where superscript G indicates evaluation at the grounding line, we obtain equations for the grounding-line migration rate at zeroth order
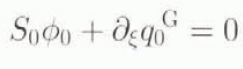
and at first order
where superscript G indicates evaluation at the grounding line.
We specify q 1 as follows. Consider the mass flux in Equation (3) in the normalized coordinates
which, upon writing
allows us to obtain q at zeroth order
and at first order
The zeroth order relationships (8) and (12) are equivalent at the grounding line, a consequence of the neutral equilibrium property. That is, for any positive span S 0, there exists a corresponding solution H 0 such that Ṡ 0 and ∂ τ H 0 are zero (Hindmarsh, 1993). The moving-boundary condition does not apply an extra constraint. The absence of a unique solution can also be deduced from the first-order Equations (9) and (13) by setting ∂ τ H 1 = 0, Ṡ 1 = 0 and also ϕ 1 = 0 (in investigating the uniqueness of the zeroth-order solution there is no first-order forcing by construction), yielding an ordinary differential equation
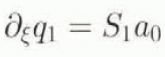
and an equivalent (from the definition of ϕ; Equation (10)) static margin condition
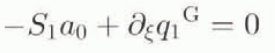
which, once we have specified the dependence of q 1 on H 1 , may be solved for H 1 upon specification of S 1 .
Let us consider steady configurations of the first-order perturbation. Substitution of Equation (17) into Equation (18) yields
where we have used the consequence of steady state and continuity that
Satisfaction of the zero flux condition at the divide ξ = 0 shows the constant of integration to be zero and we obtain the first-order differential equation
whose solution depends on the specific forms of H 0 and S 0. Note that at the divide
Let us consider the time-dependent case again. Since q1 is a linear function of S 1 , H 1 and ∂ ξ Η 1 , we can construct a separable solution
where S c1(τ) is an unknown amplitude of the first-order span. The same time-dependence as H 1 follows because of linearity. We use the construction
where
to write Equation (9) as
where λd is an eigenvalue of the problem. The boundary conditions are
i.e. a zero-flux condition at the divide and an Archimedean condition at the margin. We can see immediately from Equation (21) that solution of the equation
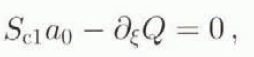
(which is, apart from notation, exactly the same as Equation (18)) yields a zero eigenvalue provided the denominator of the righthand side is zero, which is generally satisfied. This feature is obtainable for any physically reasonable S 0, H 0, showing that the marine ice sheet is neutrally stable. Computation of the other eigenvalues and all the eigenvectors requires introduction of the moving-boundary condition (13), which in separable form is
A convenient way of solving the eigen problem in Equations (21) and (23) is to carry out a finite-difference discretization and solve the resulting algebraic eigenvalue problem. Hindmarsh (unpublished) discussed finite-difference discretizations for ice-sheet eigenvalue problems. The eigen problems (21) and (23) are conveniently rewritten
The discretization used to compute the normal modes of this equation set is given in Appendix A and in particular a spectrum of eigenvalues 
, i ∈ N are approximated by a finite sequence. Results are discussed below.
5.2. Explicit time-stepping scheme and stability analysis
We now examine the stability of a numerical marching scheme to solve the marine ice-sheet evolution equation. The evolution equation
is discretized according to an explicit scheme where superscript k refers to the time level and subscript i refers to the spatial point. This explicit scheme may be written
where ∆ t represents the time step,
and
There is a virtual point such that 
which permits definition of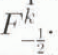 
. The stability of this scheme can be assessed by computing its Jacobian (outlined in Appendix B). The eigenvalues and eigenvectors can then be calculated using standard techniques.
For stability, we require that the eigenvalues of the iterated map |
| ≤ 1. It is more useful to compare the iterated-map eigenvalues 
with those for the dynamical system 
. For a given mode i. the time solutions are given by
for identical initial conditions, where superscripts d, and m indicate the solutions for dynamical system and iterated map, respectively. Dividing these equations and taking logs yields
If the linearized dynamics of the iterated map and dynamical system are equivalent, we therefore expect
This provides a cross-check on our algorithms. Numerical results comparing the dynamical system and the iterated map are presented in the next section.
6. Solution to the eigen problem
6.1. Some steady profiles
We need to construct some steady profiles about which to perturb the ice sheet. This is easily accomplished by integrating from the grounding line to the divide, as the flux is known at any point. In all cases, we choose C = 1. At any grid centre i + ½, the flux equation
is satisfied by solving the algebraic equation for H k . with known H k+1. The grounding-line elevation is prescribed by the flotation condition (1). Some profiles for v = 3, m = 5 are shown for different prescribed spans and different prescribed accumulation raies are shown in Figure 2. In all cases, the prescribed zeroth-order span was S 0 = 1. The three models 1,2 and 3 had flat bases with b = (−1, −0.5, −0.25), respectively. The results agree with intuitive expectation; shallower water (i.e. a smaller grounding-line thickness) leads to a greater slope at the grounding line and a thicker ice sheet.
Fig. 2. Steady marine ice-sheet profiles for different depths to base. Horizontal axis ξ, vertical axis z, where δ is an operator representing a small change. Using these expressions, the N + 2 equations comprising the iterated map can thus be expressed in differentiated form as δyk+1 = Jmδyk. The stability properties of the iterated map can be assessed by computing the eigenvalues of Jm using standard techniques (Wilkinson, 1965).
6.2. The eigenvalues
Eigenvalues for the dynamical scheme and equivalent eigenvalues for the iterated map have been computed and are shown in Table 1. These show that there are two zero eigenvalues and then a sequence of decreasing eigenvalues. The eigenvalues can be interpreted as decay constants with an associated scale inverse time-scale [a]/[H]. The eigenvalues belonging to the governing partial differential equation (PDE) and the iterated map are identical to two significant figures. Note, in particular, that the numerical scheme yields zero eigenvalues, giving it the same neutral stability properties as the governing equation. No positive eigenvalues, which would have indicated physical or numerical instability; were found.
Table 1. Table of computed eigenvalues. Column numbers refer to the model, while the letter A refers to the eigenvalue 
computed from the perturbation of the dynamical system and N to the equivalent quantity 1 / ∆t log (
) computed from the iterated map provided by the explicit marching scheme. Discretization interval ∆ξ = 0.005 and the time step in the explicit marching scheme was ∆t — 
.
Scale theory and more detailed computations (Hindmarsh, unpublished) suggest that the slowest relaxing mode for land-based ice sheets should have eigenvalues around m + v, while the eigenvalues reported here are substantially less. This means that the linearized time constant of a marine ice sheet is substantially longer than those for land-based ice sheets.
6.3. The eigenvectors
The eigenvectors for model 1 (specified in section 6.1) are plotted in Figure 3. These show the eigenvector components arranged in order of increasing ξ, with, the span-shift component at the righthand end. It should be noted that the generating eigen problem is not self-adjoint and that these eigenvectors are therefore not orthogonal.
Fig. 3. First six eigenvectors for the perturbation about model 1 represented in space (*) and with their associated span projections (○).
Excepting one of the pair of eigenvectors with associated zero eigenvalue, all the eigenvectors take on a value of exactly zero at the grounding line. The second eigenvector alone has a non-zero value at the grounding line. One would expect one of the eigenvalues to have this property, as this allows the solution to admit changes in sea level, which necessarily cause the elevation at the grounding line to change. That linear combination of the first and second eigenvectors, which has value zero at the divide, created the vector corresponding to a contraction/expansion of tin coordinate system, which is what happens during a sea-level rise.
The first eigenvector corresponds to a shift along the equilibrium manifold. This was demonstrated numerically by comparing it with the solution to the linear ordinary differential equation (ODE) (19) for the shift along the equilibrium manifold. Agreement was found to four significant figures. The third eigenvector and all the remainder have negative eigenvalues, indicating linear Stability. The third and first eigenvectors are colinear, apart from their span component.
6.4. Stability
Hindmarsh (1993) demonstrated the neutral equilibrium property for a model with a reduced set of degrees of freedom but failed to demonstrate it with a numerical model. We have shown analytically that the uncoupled marine ice-sheet model has a zero eigenvalue whenever the steady solution lies on the equilibrium manifold, and we have now devised a numerical model which exhibits stability on the equilibrium manifold. The finite-difference model of Hindmarsh (1993), while consistent with the partial differential equations, exhibited a slowly growing long wavelength instability. This unphysical instability has been tamed and has been shown to be tamed in the present model. Nevertheless, marine ice sheets possess a dynamical property, the zero eigenvalue along the equilibrium manifold, which necessitates some care in the construction of numerical models.
Since not all the eigenvalues are negative in sign, we cannot say that the system is asymptotically stable. Normally, in assessing the stability of systems with zero eigenvalues, the second-order stability needs to be considered. We have shown that there exists a zero eigenvalue along the equilibrium manifold, with the implication that in this sub-space stability has been considered to all orders. We should be careful in presuming, however, that this means the non-linear stability of the system has been fully understood. Nevertheless, the results from the next section do not suggest that anything highly anomalous is happening. The results in the next section do not indicate instability, so we should tentatively state that marine ice sheets are Lyapunov stable.
7. Integrations of the explicit scheme
We carry out some numerical integrations of the steady profile corresponding to model 2 , where b = −0.5, changing accumulation rate and sea level.
The algorithm has been tested by checking it against numerical solutions of the first-order Equation (13). The equations have been expressed in dimensionless form and the results apply to any combinations of the scales [H] , [S], [C] , [a]chosen to satisfy
In particular, we note that the time-scale [t] = [H]/[a].
In experiment 1 reported below, the discretization was (∆ t , ∆ ξ ) = (10−4, 2 × 10−2) while in experiment 2 the discretization was (∆ t , ∆ ξ ) = (10−5, 10−2). The scheme is of accuracy O(Δ t , ∆ ξ ).
7.1. Experiment 1: change in accumulation rate
The accumulation rate was increased by 25% and the system left to equilibrate for two time units, Subsequently, the accumulation rate was restored to its original value. The span increased from 1.0 to a new equilibrium value 1.024 and decreased alter the accumulation rate was reduced to a value 1.00. The divide thickness increased from 1.35 to 1.40 and returned to 1.35 (Fig. 4). The key point is that this change was essentially reversible.
Fig. 4. Elevation at the divide (vertical axis) as a function of time (horizontal axis) for experiment 1, where the accumulation rate was increased and decreased (solid line) and experiment 2, where sea level was raised and lowered (dotted line).
7.2. Experiment 2: change in sea level
Sea level was raised by 20% over half a time unit and the system left to equilibrate for two time units. Subsequently, sea level was lowered to its original position over half a time unit and left to equilibrate over two time units. Figure 4 shows the results; during the phase of rising sea level, the divide elevation decreased. I do not understand why this should happen; the ice should be simply floated off and the inland ice undisturbed, as in the shallow-ice approximation the flow of the inland ice is not affected by the proximity of the grounding line. During the reverse phase, the ice sheet has recovered its original configuration almost exactly. A study of the effect of grid size on the cycle showed that the minimum span increased rather slowly with decreasing grid size and the result reported here would almost certainly he changed by further subdivision of the computational grid.
It seems that small errors introduced, presumably by the moving grid term Ṡξ∂Η/∂ξ, are non-linearly amplified by the flux relationship, which is very sensitive to small changes in ice-sheet elevation. Since the marine ice sheet is at best only Lyapuuov Stable, errors are not dissipated as they are in land-based ice sheets and the effect is cumulative, leading to a steady drift from the true solution as errors are injected into the flux relation from the moving grid term. In truly dissipative systems, errors decay and thus erroneous solutions decay on to the true solution. An example of this is shown in Figure 12 of Hindmarsh and others (1987) and this has been discussed on p. 207–08.
8. Conclusions
This paper has been concerned with confirming the dynamical consistency of a finite-difference scheme for solving the uncoupled marine ice-sheet equation and the governing equations. An uncoupled marine ice sheet is one where the influence of the ice-shelf stress fields is not apparent upstream of a narrow boundary layer near the grounding line. The kinematical formula for grounding-line advance and retreat used in this paper respect mass conservation but, in the transition zone (which has horizontal length scale of a few ice-sheet thicknesses), the velocity is not computed correctly for both confuted and unconfined ice sheets. This does not mean that mass is no longer conserved. The assumption used in this paper, which is based upon strong computational evidence, is that the incorrectly computed flow in the transition zone does not affect the large-scale flow of the ice sheet and that the flow in this zone is stable in the sense that steady ice-sheet profiles can be maintained.
The uncoupled marine ice-sheet system has been shown to possess a zero eigenvalue corresponding to shifts along the equilibrium manifold. This is the line in phase space which defines corresponding equilibrium thicknesses and spans, and should be contrasted with land-based ice sheets, which simply have a number of points in phase space where the thickness and span are in equilibrium. An explicit finite-difference scheme has been constructed which maintains long wavelength stability. In particular, this scheme has been shown to possess an equilibrium manifold, Like all explicit schemes for ice-sheet flow, this scheme shows instability at short wavelengths when time steps are too long but this problem could presumably be rectified by use of an implicit scheme. This is the first time that a numerical model of a marine ice sheet has been shown to be dynamically consistent with the governing equations. Such demonstrations of consistency are a necessary prerequisite for modelling studies of marine ice-sheet stability. Moving-grid methods are the easiest way to assess the stability of a numerical scheme for the marine ice-sheet system.
Numerical integrations do not suggest the system is non-linearly unstable but we have yet to devise a scheme which computes the response to sea-level rise correctly. Evidently, errors accumulate as a result of the zero eigenvalue rather than dissipating as they do in other ice sheets. This effect seems to manifest itself more when the ice sheet is being forced by sea-level changes than by accumulation-rate changes.
Acknowledgements
I should like to thank M. Verbitsky for pointing out an error in Hindmarsh (1993) and drawing my attention to A. Salamatin’s work on moving boundaries. I had an instructive conversation with J. McWilliams about metastability.
Appendix A
Construction of the algebraic eigenvalue problem for the perturbation of the governing equations
We divide the domain ξ ∈ [0, 1] into N intervals and specify X at N + 1 points indicated by a counting index, i ∈ (0, N). The interval size is denoted by Δ ξ = 1/N. At the grid centres, we compute
and similarly for Q k−½ and discretizo according to
where
For the point i = 0 where the boundary condition is zero flux (see Equation (22)) we simply use a symmetry condition with a virtual point X −1 = X 1 and coefficients
to obtain
We may then discretize Equation (24) for i ∈ (0, N – 1) according to
and
and where
These relations can be written as a matrix eigenvalue problem
where y T = [X 0, …, Χ N , S c1] and the eigenvalues and eigenvectors computed using standard techniques (Wilkinson, 1965).
Appendix B
Stability of an explicit marching scheme
In this Appendix, we carry out one step of the analysis of the stability of the iterated maps in Equations (25) and (27) by computing their Jacobians. The time index is superscript k and the space index is subscript i. To this end, we form
Where F is defined in Equation (26) and
where
This allows us to write
which, upon defining
yields
Symmetry around the divide yields a special form at i = 0 which is
We can also write down
and
The next step is to consider the span-evolution equation
and form
If we note
and
we can write
Finally, we note that
and that we can compute
where δ is an operator representing a small change. Using these expressions, the N + 2 equations comprising the iterated map can thus be expressed in differentiated form as
The stability properties of the iterated map can be assessed by computing the eigenvalues of J m using standard techniques (Wilkinson, 1965).
