Introduction

Large ice-stream—ice-shelf systems play fundamental roles in the dynamics of the Antarctic ice sheet (Reference Thomas and BentleyThomas and Bentley, 1978), and the relationship of glacial retreat and advance has been discussed in the context of climatic changes. Lambert Glacier and Amery Ice Shelf are the largest such system in East Antarctica and they discharge an inland catchment area of about 870 000-902 000 km² (Reference Giovinetto and BentleyGiovinetto and Bentley, 1985; Reference MclntyreMcIntyre, 1985). Satellite-altimeter observations from satellite missions spaced about a decade apart—the 1978 Seasat and the 1987–89 Geosat Exact Repeat Mission (ERM)— provide information that enables us to approach this problem.

Lambert Glacier is the only major Antarctic ice-stream—ice-shelf system within the ± 72° orbital coverage of Seasat and Geosat (for location map, see Reference Lingle, Lee, Zwally and SeissLingle and others (1994)). Pioneering work on the Amery Ice Shelf was carried out by Australian expeditions during 1962-65 and 196–1 (see, e.g. Reference Budd, Corry and JackaBudd and others, 1982). Previous altimeter-based studies of this highly dynamic area have been carried out by Reference Brooks, Williams, Ferrigno, Krabill, Oliver, James and JagoBrooks and others (1983), Reference Partington, Cudlip, Mclntyre and HelePartington and others (1987) and Reference Zwally, Stephenson, Bindschadler and ThomasZwally and others (1987), using data from Seasat, and by Reference Herzfeld, Lingle and LeeHerzfeld and others (1993) using data from the Geosat ERM.

Changes in the Earth’s climate result in mass changes of ice streams and glaciers but the mechanism is far from being understood. In principle, warming leads to reduction of ice. Another possible scenario is that, in a slightly warmer climate, precipitation increases and higher precipitation over Antarctica adds mass to the ice, which will not melt, as even after a slight increase temperatures will be below freezing. Mass changes are, however, difficult to study. The calving fronts of the ice

shelves can be considered the margins of the ice sheet but the episodic nature of iceberg calving means that large changes in the positions of ice-shelf fronts may not be indicative of the mass balance of their inland catchment areas. The grounding line of an ice stream is more difficult to detect but it migrates horizontally in response to thickening and thinning of the ice stream, and thus is a better indicator of the ice-stream dynamics. Expected elevation changes are small in relation to various geodetic corrections applied in the satellite-data processing, instrumental errors, etc. For a given thickening rate, displacement of the grounding line, however, is apparent already on visual inspection of the kriged maps (because the bed slope is small, as well as the surface slope (personal communication from I. Allison)), even if one takes into account that the apparent position of the grounding line, corresponding to a break in slope, is only an approximation of the true position of the grounding line.

In this study, we address the question whether the positive net balance calculated for the entire Lambert Glacier catchment area by Reference AllisonAllison (1979) and Reference MclntyreMcIntyre (1985) and for the Lambert Glacier system by Reference AllisonAllison (1979), from global mass-balance estimates, is supported by a measurable advance of the grounding line between 1978 and 1987–89. Geostatistical methods for grid calculation and error analysis have been adapted and developed for evaluation of satellite-altimeter data over ice, and found suitable for detecting the grounding line (Reference Herzfeld, Lingle and LeeHerzfeld and others, 1993; of Reference Partington, Cudlip, Mclntyre and HelePartington and others, 1987). As essentially the same method will be applied here to map the lower Lambert Glacier and Amery Ice Shelf region in a comparative study, the reader is referred to that paper for glaciological background and methodological details. The results are compared to the mean changes in surface height on lower Lambert Glacier during the same time interval computed by Reference Lingle, Lee, Zwally and SeissLingle and others (1994) from cross-over analysis of the Seasat and Geosat ERM altimetry.

Data

This study is based on Geosat ERM data and Seasat data. As the Seasat was only in operation for a period of about 3 months in austral late winter (10 July— 9 October 1978), time windows corresponding in season to the Seasat operation time have been selected from the Geosat ERM data in 1987, 1988 and 1989 to avoid seasonal effects such as changes in penetration depth (Reference Ridley and PartingtonRidley and Partington, 1988). The altimeter-derived surface heights are referenced to Goddard Earth Model (GEM) 1'2 orbits (Reference MarshMarsh and others, 1989) and corrected for tracking errors using the method of Reference Martin, Zwally, Brenner and BindschadlerMartin and others (1983), for atmospheric effects and solid earth tides (of.Reference Zwally, Bindschadler, Brenner, Martin and ThomasZwally and others, 1983), for slope-induced errors (CD. Reference Brenner, Bindschadler, Thomas and ZwallyBrenner and others, 1983) and for water-vapor effects by the ice-sheet altimetry group at NASA/Goddard Space Flight Center, Green-belt, Maryland, U.S.A. The surface elevations are given relative to the WGS 84 ellipsoid.

The data, originally referenced to geographical coordinates, are transformed into Universal Transverse Mercator (UTM) coordinates for geostatistical evaluation, using 70° E as central meridian. The area is bounded by 66-75° E and 6–2.l° S, and is rectangular after transformation into UTM coordinates with dimensions 308 km east—west by 444 km north—south. The data distributions are shown on ground-track maps given in Figure 1a for Seasat data and in Figure 1b for Geosat data from the combined “Seasat seasons” in 1987—89.

Fig. 1. Ground-track maps in the area of Lambert Glacier and Amery Ice Shelf. a. Seasat ground tracks, 1978. b. Geosat-ERM ground tracks, for time frames corresponding in season to Seasat survey, in 1987—89.

Geostatistical Evaluation

From the corrected along-track data, a digital terrain model (DTM) with 3 km grid interval is calculated for each data set (Seasat and Geosat “Seasat seasons”). The 3 km grid interval is chosen because that is roughly three times the ice thickness in the vicinity of the grounding zone of Lambert Glacier; the DTM is thus suitable for numerical ice-flow models that incorporate the effects of longitudinal stress gradients.

The geostatistical method applied here for DTM calculation and error analysis is essentially the same as that used by Reference Herzfeld, Lingle and LeeHerzfeld and others (1993) to map the grounding zone of Lambert Glacier. Because the grounding line is the feature of most interest in this topographically complex region, a Gaussian variogram determined for a small sub-area around the grounding line is used in the kriging process.(The parameters characterizing the variogram are nugget effect 250 m², quasi-sill 593 m², quasi-range 18 000 m; of. equations (1)–(5) and figure 4 in Reference Herzfeld, Lingle and LeeHerzfeld and others (1993) The estimation of each grid node is based on a 16 point neighbourhood, selected in a quadrant search. Ordinary kriging is employed, because universal kriging of higher order results in distortions of the DTM when fitting the internal trend across large gaps in the ground-track pattern (see Fig. I).

Resultant Maps

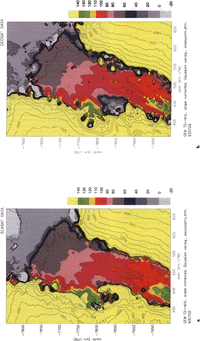
Maps contoured from the DTMs are shown in Figure 2a for the Seasat-altimeter data and in Figure 2b for the Geosat-ERM data from “Seasat time windows” in 1987–89. Both data sets yield spatially continuous maps showing the main topographic features of the area, and this is the case for Seasat altimetry despite the less effective on-board tracker which resulted in reduced coverage (of. Figures 1a and b; of figure 2 of Reference Brooks, Williams, Ferrigno, Krabill, Oliver, James and JagoBrooks and others (1983), and figure 4 of Reference Zwally, Stephenson, Bindschadler and ThomasZwally and others (1987)).

Fig. 2. Topography of Lambert Glacier and Amery Ice Shelf. D TMs calculated using ordinary kriging with a Gaussian variogram model. Grid interval 3 km. UTM coordinates, area about 66–75°Eand 6–2.1°S. Elevations in m above WGS 1984 ellipsoid, GEM- T2-referenced, slope-corrected and water-vapor-corrected, a. From Seasat altimeter data (1978). b. From Geosat-ERM altimeter data (1987–89), from time frames corresponding in season to Seasat survey. The grounding-line proxy (100m contour) is farther seaward than in a.

The most problematic feature on both maps is the calving front of Amery Ice Shelf; which appears as a sloping ledge in the Seasat map (Fig. 2a) and as a fuzzy area of ice front on the Geosat map (Fig. 2b). One reason is that ordinary kriging is a least-squares-based averaging operation, and therefore does not preserve near-vertical cliffs, even if they are represented in the data. The ice-shelf front, however, is not well represented in the height data because of the 11 km radius of the beam-limited radar footprint. A method for extracting the front location from wave-form data has been described by Reference Thomas, Martin and ZwallyThomas and others (1983). For the Geosat data, the fuzziness of the appearance of the ice front may be due to actual changes in the ice-front's location during the 3 years of survey.

The Seasat map has an overall smoother appearance than the Geosat map. This may be attributed to the lesser data density, which causes a larger average search radius for the grid nodes and therefore a greater smoothing effect through kriging. Another difference between the two maps is the representation of the margin. On the Geosat map, the ice thickness appears to be reduced particularly along the eastern margin, which can be partly explained by stronger vertical strain rates within the ice-shelf shear margins and partly by the so-called “snagging effect” of the altimeter (for a discussion, see Reference Herzfeld, Lingle and LeeHerzfeld and others (1993)).Reduced surface elevations along the margins are less prominent on the Seasat map.

Changes In Position Of Grounding Line

On the floating Amery lee Shelf, the positions of the 60, 70, 80 and 90 m contours differ only slightly between Seasat and Geosat ERM. The 90 m contour appears to have advanced a little (about 3km), the 80m contour even less. The slope break at the 100 m contour that can be recognized on both maps is taken as a proxy for the position of the grounding line. This contour divides the more rugged, undulating topography of the grounded Lambert Glacier from the smoother surface down-glacier that is indicative of floating ice. The apparent grounding line is very irregular. The patchy areas seaward of the grounding line appear to be ice rises caused by sea-floor shoals projecting into the bottom surface of the ice shelf. The entire area of the meandering 100 m contour and ice rises can be considered as the grounding zone. The location of the grounding line on theGeosat map is broadly consistent with the location determined from recent field observations by I. Allison (personal communication). For comparisons with locations given in previous investigations, see Reference Herzfeld, Lingle and LeeHerzfeld and others (1993).

A visual comparison of the location of the 100 m contour on Figure 2a and b shows that the grounding line lies farther north on the Geosat map than on the Seasat map. The most prominent difference is that the ice rises attributed to sea-floor shoals extend much farther north on the Geosat map and terminate closer to the 90 m contour. The mean advance of the grounding line was measured as approximately 10–12 km.

Error Analysis

The standard error of the kriged DTMs is estimated using equation (8) of Reference Herzfeld, Lingle and LeeHerzfeld and others (1993), which is derived by propagating noise levels through the kriging equations and depends on the noise levels and the kriging weights. A map of the noise levels in the Geosat ERM altimetry, estimated using the variogram method (Reference Lingle, Brenner and ZwallyLingle and others, 1990; Reference Herzfeld, Lingle and LeeHerzfeld and others, 1993) is given in Reference Lingle, Lee, Zwally and SeissLingle and others (1994). The distribution of the estimated standard error (Fig. 3) for the Geosat DTM mirrors the topography. On the flat Amery Ice Shelf, the standard error is mostly below 3 m. In the grounding zone of Lambert Glacier, the error increases to about 3-6 m, with higher values up-glacier over the rougher topography of the grounded ice stream. The Seasat and Geosat altimeters were so similar in design that the difference in instrumental error is minor (3 cm rms over the oceans for Geosat compared to 5 cm rms for Seasat for 1 s¹ along-track data (Reference Sailor and LeSchackSailor and LeSchack, 1987); therefore, the standard error of the Seasat DTM can be taken as similar to that shown in Figure 3. The values shown on the error map (Fig. 3) are an expression of the smoothing effect of the kriging operation (ordinary kriging is a moving-window averaging procedure) and therefore indicate the local inaccuracy of the maps (e.g. crevasses do not show), and do not translate into a systematic error in the location of the grounding line.

Fig. 3. Standard error of the kriged map shown In Figure 2b.

A source of systematic error that affects the apparent location of the grounding line, pointed out by Reference Partington, Cudlip, Mclntyre and HelePartington and others (1987), results from the altimeter “seeing” the grounding line up-slope of its actual location because of the break in slope. This effect should be largely accounted for by slope correction. In any case, the apparent position of the grounding line in both the Seasat and the Geosat DTMs should be equally affected.

The geographically correlated, systematic orbit bias in this region between Seasat and Geosat ERM has been estimated as 0.083 ± 0.131 m by Reference Lingle, Lee, Zwally and SeissLingle and others (1994), i.e. the Geosat ERM surface height is systematically slightly higher. This offset accounts for an apparent northward displacement of the grounding line of about 581 ± 917 m and is small compared to the measured grounding-line advance of about 10–12 km.

Summary

Geostatistical evaluation of satellite-radar altimetry from Seasat and the Geosat Exact Repeat Mission results in high-resolution maps of complete coverage of lower Lambert Glacier and Amery Ice Shelf and the adjacent grounded ice sheet, for austral late winter (10 July-9 October, “Seasat time frame”) in 1978 and in 1987, 1988 and 1989 (combined). A comparison of the maps indicates that the grounding line of Lambert Glacier advanced approximately 10 km between 1978 and 1987–89, corresponding to a mean advance rate of about 1000 m year^-1.This advance is consistent with the recent mean increase of the surface height on lower Lambert Glacier measured with orbit cross-over analysis of the Seasat and Geosat ERM altimetry by Reference Lingle, Lee, Zwally and SeissLingle and others (1994) and with the positive net mass balance (with uncertainty range slightly overlapping zero) inferred for the Lambert Glacier system by Reference AllisonAllison (1979) and Reference MclntyreMcIntyre (1985).

The approach employed in this study is suitable for computation of a time series of DTMs of this and other areas of interest, if radar-altimeter data from recent (i.e. ERS-l) and future satellite missions are included, which will provide a useful tool to study the dynamics of the Antarctic ice sheet.

Acknowledgements

This work was supported by the NASA Polar Research Program, grants NAGW-2614 to C. S. Lingle and NAGW-2746 to U. C. Herzfeld. We thank H.J. Zwally (NASA/Goddard Space Flight Center), A. C. Brenner and J. P. Dimarzio (STX Corporation) for furnishing theretracked and slope-corrected altimetry used in this study and for assistance with reading the tapes; R. Guritz for technical assistance with the Alaska SAR Facility IIAS computing system; the Arctic Regions Supercomputing Center for CPU time on a CRAY Y-MR M98; D. Covey (University of Alaska—Fairbanks) and M. Lambert (University of California—San Diego) for programming assistance; D. Sandwell (Scripps Institution of Oceanography) for use of a colour plotter; C. Freeman (University of California-San Diego) for help with plot production; and I. Allison (Antarctic Cooperative Research Centre, University of Tasmania, Australia) for useful and informative discussions.