Introduction
Snow avalanches flow downward to the bottom of the valley and usually move along the streamline. Many avalanches occur in mountain areas every winter. An avalanche flows basically along the stream, but when the direction of avalanche velocity is different from the steepest descent line of a valley, the avalanche flow deviates from the streamline because of inertia. Such deviations sometimes significantly change the avalanche path and cause unexpected disasters.
The prediction of avalanche path by a dynamic model is one method to prevent unexpected avalanche disasters. Many dynamic models of snow avalanches have been developed. Reference IsslerIssler (1998) and Reference Naaim and GurerNaaim and Gürer (1998) developed fluid models with many equations to express the complexity of avalanche dynamics, but these require many parameters and inputs of initial conditions.
The purpose of this study is to develop a method of predicting avalanche paths that deviate from the streamline on complex surfaces for cases where there exist hardly any avalanche data for tuning the models and it is difficult to obtain information on initial conditions. Nohguchi’s (Reference Nohguchi1983, Reference Nohguchi1989) center-of-mass model is a simple model that was used in Japan. Reference Ikemoto and KitauraIkemoto and Kitaura (1998) calculated the distribution of impulsive forces acting on avalanche-protective structures. Reference Maeno and NishimuraMaeno and Nishimura (1987) and Reference Nishimura and MaenoNishimura and Maeno (1989) proposed more detailed parameters and applied them to real avalanches.
In this study, three-dimensional paths from many starting points were calculated using Nohguchi’s center-of-mass model at two sites where disastrous surface avalanches occurred.
Methodology
Equations of Nohguchi’s center-of-mass model (Reference NohguchiNohguchi, 1983, Reference Nohguchi1989) were used in this study. His equations were derived from classical mechanics on a surface of arbitrary configuration. On an arbitrary configuration that is represented by z = f(x, y), x and y are horizontal positions, z is an elevation, and the equations of motions are

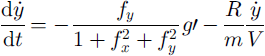
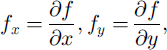
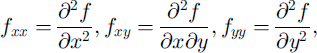
where m is mass, g is gravity, V is the magnitude of velocity and R is the magnitude of dynamic resistance.
Starting points
Reference NohguchiNohguchi (1986, Reference Nohguchi1987) pointed out that the calculation of avalanche paths from several release points simultaneously indicates the horizontal spread of avalanche paths. The maximum number of starting points in his analysis was only six. Calculation of paths from more starting points would show the horizontal spread of avalanche paths in more detail. In addition to predicting individual paths, the distribution of avalanche paths for each site may be studied. In this study, many starting points were set on a wide upstream area.
This method does not consider the volume of an avalanche, the cohesion of snow or any interaction between the test masses. Deviations of the flow caused by already deposited parts of the avalanche in the run-out zone are therefore not considered. The paths of each test mass were calculated completely independently.
Dynamic resistance
Dynamic resistance R determines avalanche dynamic characteristics in Nohguchi’s center-of-mass model. R is as follows:
where N is normal force, m is mass (assumed as constant), and V is velocity. The dry-friction coefficient μ and the coefficient 6 of drag resistance determine the dynamic characters of the movement. Reference NohguchiNohguchi (1987) had calculated surface avalanche paths with μ = 0 and 6 = 0.0025–0.007. Dry friction was ignored. Though Reference Perla, Cheng and McClungPerla and others (1980) and Reference Nishimura and MaenoNishimura and Maeno (1989) explored the dynamic resistance of an avalanche, they did not consider the effect of different starting positions. In this study, some combinations of> = 0 ∼ 0.2 and 6 = 0.0025 ∼ 0.007 were used.
Case-Studies
Two sites in Japan where surface avalanches had caused disasters were analyzed. The Runge-Kutta technique was used to solve the equations at a time step of 0.2 s. The horizontal resolution of a digital elevation map is 25 m.
Small deviations of avalanche paths on complex topography
The first disaster analyzed occurred in Niigata prefecture. It was found in March 1997 that the Yunoshima lodge in the Iide mountains was damaged during the first winter after it was built. It did not survive this first winter due to an avalanche. Though the Yoshiwara stream was near the lodge, avalanche deviation from the streamline was considered small and the position of the lodge was considered safe from avalanches. The distance from the lodge to the stream was about 30 m, and the elevation difference between the lodge and the bottom of the stream was significant. In addition, there were ridges on the right and left sides of the stream upstream of the lodge. The direction from the base of the lodge to the deposition of the second-floor debris was different from the streamline direction. There was a tree broken at 6 m height on the left streamside. A surface powder avalanche was believed to have blown off the second floor of the lodge and destroyed the ground floor. We found tracks of an avalanche in some of the upper branches of the stream during field investigation in early May, but could not specify the path and the starting zone of the avalanche that destroyed the lodge.
In this case, paths from 12 starting points were calculated with (M, 8) = (0,0.007), (0.5,0.0025), (0.1,0.0035). These values were selected based on test calculations in this area. In the test calculations, the deviations of paths calculated with smaller dynamic friction had been too large, and avalanches calculated with larger friction had stopped above the lodge.
In Figure 1, paths calculated with (μ, ) = (0, 0.007) are shown on the contour map made from a digital elevation map. The three branches in which tracks were found were labelled A-G. Paths were calculated from three starting points in branch A, four points in B and five points in C. In Figure 1b, dashed lines show the paths of avalanches that occurred in branch A or B, and solid lines show the paths of avalanches that occurred in branch C.

Fig. 1. Contour map of Yoshiwara stream. Intervals of gray contours are 10 m. Intervals of bold contours are 50 m. (b) is a magnification of the lower right square area of (a).
Branch C joins the main stream 300 m above the lodge. Though most of the calculated paths went along the stream and did not pass near the lodge, two paths calculated with (μ, δ) = (0, 0.007) from branch C deviated considerably from the stream and passed near the lodge. Branch C had no sharp bends, but many gentle bends which made the direction of the avalanche paths uniform at that junction, so that these paths meandered with the same cycle below the junction. Finally, the ridge on the left side changed the directions of two paths that had large meandering widths, and these two paths passed near the lodge. The speed of the avalanche that passed near the lodge was about 14 ms–1. The lodge was wooden and its mass was about 103 kg, so the speed would be enough to demolish the lodge.
On the other hand, 200 m above the junction, one small ridge changed the direction of the main stream considerably. The directions of avalanches that occurred in branches A and B were almost the same at the junction below the small ridge. The directions of the paths from branch C were different from those of the paths from branches A and B. The difference in the avalanche direction caused the differences in the cycle of the avalanche-path meanderings below the junction. As a result, these paths went to the left side near the lodge, and an avalanche path calculated with (μ, δ) = (0.05, 0.0025) from branch B deviated from the stream and went over the ridge on the left side.
These results showed that an avalanche in branch C could reach the lodge more easily than an avalanche running along branch A or B. We concluded that avalanche C might have struck the lodge, and that there was avalanche danger on both sides of the stream near the lodge.
Judgment for going over the ridge
The next case describes surface avalanches that went over a ridge and struck a colony. The last avalanche disaster in Sosori, Ishikawa prefecture, occurred in 1918. An avalanche struck a colony, destroying 7 houses and killing 19 people. The contour map of Sosori is shown in Figure 2. At this site there was protective forest on all slopes around the stream, and avalanches had not struck the colony for about 300 years. The avalanche danger was forgotten about and in 1912 part of the forest was cut on the right slope of the stream. Subsequently, in 1918, a surface avalanche struck a colony. It is believed that simulated avalanches with large dynamic resistance cannot go over the ridge, but simulated avalanches with small dynamic resistance can go over the ridge and strike the colony.

Fig. 2. Contour map around Sosori. Destroyed part of the colony is the lower left gray area.
In this case, starting points were set on a wide area of the upper stream. Paths were calculated from the 361 starting points, with different dynamic resistance (μ, ) = (0 ∼ 0.2, 0.0025 ∼ 0.007). The A-G line in Figure 2 was used to decide whether an avalanche reached the destroyed colony. Avalanches that passed the A-B line were considered as avalanches that reached the colony while those that passed the B-C line were considered as avalanches that did not reach the colony.
Figure 3 shows the number of starting points from which avalanches reached the colony. Resistance increases as the number of starting points decreases. The higher the speed, the less likely the avalanche is to follow the bend. The condition for an avalanche also depends on the starting point.

Fig. 3. The number of avalanches that reached the colony.
Figure 4 shows the distribution of starting points from which avalanches reached and did not reach the colony in function of dynamic resistance. There is no clear boundary for these points, and the boundary does not depend on elevation.

Fig. 4. Starting points set on the upper stream. White circles are the starting points from which avalanches reached the colony. Black circles are the starting points from which avalanches did not reach the colony.
Figure 5a shows paths of avalanches that reached the colony, and Figure 5b those that did not. The former did not have large meanderings, but the latter did, with similar cycles near the stream bend. These meanderings were similar to the stream bend. When the meanderings synchronized to the bend of the stream, avalanches had gone along the stream and did not go over the ridge.

Fig. 5. Avalanche paths calculated with (μ, δ) = (0.1, 0.0035). (a) Paths of avalanches that reached the colony; (b) paths of avalanches that did not reach the colony.
The velocities of the avalanches on the D-E line are shown in Figure 6. The velocities of avalanches that reached the colony were compared to the velocities of those that did not. The x axis shows the number of starting points. Starting point No. 1 was the lowermost, leftmost point, and the series proceeded towards the right. After the rightmost point, the number order was restarted from the leftmost second-lowest point. The numbering was done according to this sequence. The y axis shows the velocity of the avalanches on the D-E line. Black points existed within the range of gray points. Velocities of avalanches that went over the ridge were not very different from the velocities of avalanches that did not.

Fig. 6. Avalanche velocities on D-E line in Figure 3. Gray points are velocities of the starting points from which avalanches reached the colony. Black points are velocities of the starting points from which avalanches did not reach the colony.
At this site, avalanches with small dynamic resistance and cycles of meanderings different from the stream bend would go over the ridge easily. The height of the ridge between the colony and the stream was obviously not enough to protect the colony from the avalanche. Gutting the protective forest on the slope near the stream would be very dangerous for the colony.
Conclusions
We have calculated paths of avalanches from many starting points by the center-of-mass model with the dynamic resistance μ = 0 ∼ 0.2, 6 = 0.0025 ∼ 0.007 for sites where surface avalanches caused disasters.
As a result, the center-of-mass model calculates paths of avalanches that deviate from the streamline and which may have caused disasters. Most of the model avalanches start to meander when they reach the stream. As the avalanche flows further down, the width of the meanderings becomes smaller and the avalanche follows the stream. Sharp bends of the streamline restart meandering of the model avalanches. Meanderings cause deviations from the streamline and sometimes significant changes to the avalanche’s paths, like going over a ridge.
Though the avalanche-path meanderings depend on dynamic characteristics of an avalanche, it is difficult to specify the parameters before avalanches occur. It would be necessary to simulate several avalanches from different release zones and with different friction parameters to predict paths of the avalanche that deviate from the stream. These calculations are useful to sites that do not have avalanche records or where topography or vegetation has been changed by ground slides or tree cuts.
This method has limitations. The model cannot predict a stop of avalanche precisely. The distance of avalanche flow is overestimated. The model does not consider the behavior of a flowing material. The method should not be applied to deposit zones of large avalanches. Therefore it cannot be concluded from the results that points not reached by the model avalanche are safe, or that preventing snow from being released only from points from which test masses endanger a certain location reduces the danger at this location.








