1. Introduction
The energy balance at the glacier–atmosphere interface is the key control of the interaction between glaciers and climate and a key step in the study of the mass balance of glaciers. A component of the surface energy balance that is often neglected in numerical studies is heat conduction into the snow- and ice packs (also referred to as subsurface flux), which is commonly assumed to be small during the ablation season when melting is taking place (Reference HockHock, 2005). In these conditions, many models assume the snowpack to be at melting point (the zero-degree assumption). This is not the case at night and for certain climatic conditions (e.g. strong radiative cooling in dry climatic settings), and can lead to an overestimation of modelled melt, since part of the energy that goes into heating the snowpack to melting point in the real world is used for melt by the models. The insulating properties of snow (e.g. that its thermal conductivity is smaller than that of ice (Reference OkeOke, 1987)), can prevent efficient compensation of the radiative losses, making the zero-degree assumption more critical for snow-covered glaciers than for exposed ice. Several studies have used and validated energy-balance models that do not include the subsurface heat flux, showing that they can be successfully used for simulation of melt (Arnold and others, 1996; Reference Hock and NoetzliHock and Noetzli, 1997; Reference Brock and ArnoldBrock and Arnold, 2000; Reference Favier, Wagnon, Chazarin, Maisincho and CoudrainFavier and others, 2004; Reference Sicart, Wagnon and RibsteinSicart and others, 2005; Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others, in press). Other works have incorporated a heat-conduction scheme into both point (Reference Greuell and KonzelmannGreuell and Konzelmann, 1994; Reference Wagnon, Ribstein, Kaser and BertonWagnon and others, 1999; Reference Greuell and SmeetsGreuell and Smeets, 2001) and distributed energy-balance models (Reference Klok and OerlemansKlok and Oerlemans, 2002), but validation of the heat-conduction component is difficult because of lack of data, and no evidence of its accuracy is presented in any of these studies. Reference Greuell and OerlemansGreuell and Oerlemans (1986) have demonstrated that neglecting internal heat conduction leads to a considerable overestimation of melt at high elevations. In recent work, Reference PellicciottiPellicciotti and others (in press) looked into the importance of including the exchange of heat into the snow- and ice pack on a site in the dry Andes of central Chile. The authors concluded that, at the elevation of the study site (3127ma.s.l.), the heat flux into the snowpack was not a major component of the energy balance, and neglecting it only resulted in an overestimation of total melt at the end of the season of ∼2%. Evidence on the applicability of the zero-degree assumption and on the magnitude of the heat-conduction flux over an ablation season is therefore not conclusive.
The aim of this work is to test the zero-degree assumption and to quantify the error that is made by neglecting the subsurface flux in the calculation of the glacier energy balance in comparison with simulations that account for it. For this purpose, we run a physically based energy-balance model at several locations characterized by different altitudes and climatic settings, and compare model outputs obtained with and without the heat-conduction component. The model is validated by comparing simulated surface temperatures to observations of the glacier surface temperature.
The heat-conduction component for both the snow- and ice pack is based on existing studies. The subsurface fluxes are computed using a two-layer model, assuming that 36% of the net shortwave radiation is absorbed by the surface layer and that the rest penetrates into the snowpack (Reference Greuell and KonzelmannGreuell and Konzelmann, 1994). The model is run using data from automatic weather stations (AWSs) on Gornergletscher and Haut Glacier d’Arolla in the Swiss Alps collected over several ablation seasons, and data from one AWS site on Tsa de Tsan glacier in the Italian Alps. Our study also includes data from one AWS location on Glaciar Juncal Norte in the dry Andes of central Chile, where climatic conditions favour strong radiative cooling at night and the related cooling of the snowpack.
2. Study Sites and Data
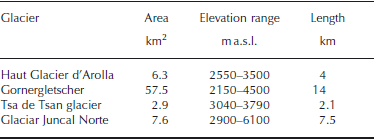
Three of the glaciers investigated are located in the European Alps, at a distance of a few to tens of kilometres from each other: Haut Glacier d’Arolla and Gornergletscher, both in the southern part of the Swiss Alps, and Tsa de Tsan glacier in the Italian Alps on the other side of Haut Glacier d’Arolla across the Swiss/Italian border. The fourth study site, Glaciar Juncal Norte, is in the dry Andes of central Chile, characterized by a different climatic regime, with dry and stable summers, precipitation close to zero, low relative humidity and very intense solar radiation (Reference PellicciottiPellicciotti and others, in press). Reference PellicciottiPellicciotti and others (in press) analyzed the impact of this climatic forcing on the ablation regime of the glacier. They showed that shortwave radiation is the dominant component of the energy balance (and greater than on alpine glaciers), and that the absence of precipitation leaves the glacier with exposed ice once the seasonal snow cover has been depleted. Conversely, an ablation season in the Swiss Alps sees fairly frequent snowfalls during summer, which have the effect of covering the glacier with a layer of snow that has higher reflectivity and insulating properties (Reference OkeOke, 1987), and thus a higher cold content than the ice (Reference HockHock, 2005). Precipitation, and thus also solid precipitation, is lower on average on Gornergletscher than Haut Glacier d’Arolla and Tsa de Tsan glacier, even though the glaciers are only ∼20 km apart. The main characteristics of the four glaciers are listed in Table 1, and details are provided by Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others (in press).
Table 1. Characteristics of the four glaciers where AWSs were installed for this work
On each glacier, AWSs were installed for the duration of the ablation season, and some were re-installed over several seasons. The AWSs measured 5min records of air temperature ( ˚ C), relative humidity (%), incoming and reflected shortwave radiation (Wm − 2), wind speed (m s − 1) and direction ( ˚ ). All sensors were set up on an arm fixed to a tripod that sat on the glacier surface and was allowed to sink with the melting of the surface, thus maintaining a nominal height of 2 m between the surface and sensors. Measurements of incoming and reflected shortwave radiation were therefore made parallel to the surface, following Reference Sicart, Ribstein, Wagnon and BrunsteinSicart and others (2001), Reference Greuell, Genthon, Bamber and PayneGreuell and Genthon (2004) and Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005).
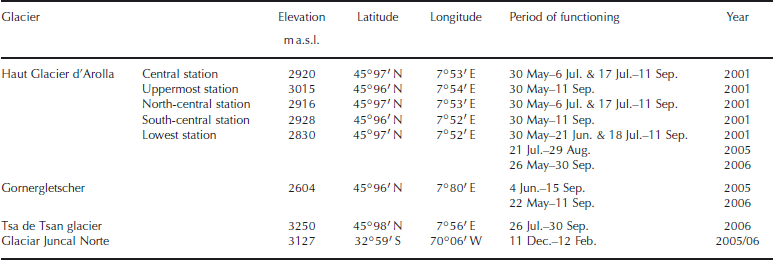
On Haut Glacier d’Arolla, five AWSs were established in the 2001 ablation season along two intersecting transects, providing a picture of the melt-rate variability across the glacier both in the accumulation and ablation area (Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005). In 2005 and 2006, only the lowest station was operated. On Gornergletscher, an AWS was set up at ∼2600ma.s.l., at the same location in both 2005 and 2006. The period of functioning was shorter in 2005 (Table 2). The AWS on Tsa de Tsan glacier is the highest of our dataset, at 3250ma.s.l. (Table 2). Measurements of air temperature at this location were not ventilated. On Glaciar Juncal Norte an AWS installed on the glacier tongue, at 3127ma.s.l., provided meteorological input data for 2 months of the ablation season (Reference PellicciottiPellicciotti and others, in press). Station characteristics and period of functioning are listed in Table 2. All meteorological data were aggregated into hourly values and used as input to the energy-balance model.
Table 2. Characteristics and period of functioning of the AWSs at the four study sites: Haut Glacier d’Arolla (2001, 2005 and 2006), Gornergletscher (2005 and 2006), Tsa de Tsan glacier (2006) and Glaciar Juncal Norte (2005/06). Coordinates are given in latitude and longitude
The Haut Glacier d’Arolla dataset is described in detail by Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005), while the Gornergletscher and Tsa de Tsan glacier measurements are discussed by Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others (in press). For the Juncal Norte dataset and field campaign the reader is referred to Reference PellicciottiPellicciotti and others (in press).
We also have surface-temperature data measured with an infrared thermometer at Haut Glacier d’Arolla lowest station in the 2006 ablation season. We use these observations to validate the internal snow and ice temperature simulated by the energy-balance model.
3. Methods
3.1. The energy-balance model
The glacier surface energy balance is computed from the energy-balance equation:
where Q M is the energy available for melt, Q I is the net shortwave radiation flux, L is the net longwave radiation flux, Q H and Q L are the turbulent sensible- and latent-heat flux, respectively, and Q S is the conductive-energy flux in the snow/ice, or subsurface flux. The energy fluxes are assumed positive if directed toward the surface (e.g. Reference Röthlisberger and LangRöthlisberger and Lang, 1987).
The shortwave radiative flux is computed from measurements of incoming and reflected shortwave radiation at the AWSs. The longwave radiation flux is modelled: outgoing longwave radiation, L↑, is computed from the Stefan–Boltzmann relationship, assuming that the surface radiates as a black body (emissivity equal to 1 for both snow and ice) (Reference OkeOke, 1987; Reference Greuell and SmeetsGreuell and Smeets, 2001). L↓ is also calculated from the Stefan–Boltzmann relationship, in which the emissivity is a function of air temperature, cloud type and cloud amount (Reference Brock and ArnoldBrock and Arnold, 2000). Cloud amount n (with n = 1 for complete cloud cover and n = 0 for a clear sky) is computed from the comparison of measured incoming shortwave radiation with the modelled incoming shortwave radiation under a cloud-free sky (Reference Brock and ArnoldBrock and Arnold, 2000). Since incoming shortwave radiation is zero at night, we assume that the cloud amount at night is equal to the mean value of the afternoon before. The cloud-type constant is assumed to be 0.26 following Reference Braithwaite and OlesenBraithwaite and Olesen (1990).
Q H and Q L are computed using the bulk aerodynamic method, which requires wind speed, air temperature and humidity to be measured at only one height above the surface (usually 2 m above the surface) (Reference MunroMunro, 1989; Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others, 1998; Reference Brock and ArnoldBrock and Arnold, 2000; Reference Denby and GreuellDenby and Greuell, 2000). The two fluxes depend additionally on the stability correction factors for momentum, heat and humidity, the Monin–Obukhov length scale (Reference ObukhovObukhov, 1971) and the scaling lengths for aerodynamic roughness (z 0), temperature (z t) and humidity (z e). In the model, z t and z e are computed as functions of z 0 using the roughness Reynolds number, Re*, following Reference AndreasAndreas (1987). The aerodynamic roughness, z 0, is evaluated following the simple scheme of Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others (2005), in which a constant z 0 value is assigned to the three main surface types: z 0 = 0.1 mm for fresh snow, z 0 = 1.0 mmfor snow after snowfall when melting has taken place and z 0 = 2.0 mm for ice. These values are in agreement with mean values reported in the literature (e.g. Reference Brock, Willis and SharpBrock and others, 2006).
The heat conduction through the snow- and ice pack, Q S, is computed following Reference Greuell and KonzelmannGreuell and Konzelmann (1994) and Reference Koh and JordanKoh and Jordan (1995), assuming that the system, composed of the atmosphere, the glacier surface and the subsurface snow- or ice pack, is one-dimensional:
and we use a simple two-layer subsurface model (Reference OkeOke, 1987), in which the heat flux exchanged between adjacent layers is computed as
where ΔQ S is the energy used to heat the snow- or ice pack at the surface, and C s is the heat capacity of the snow, C s = ρ s c s, where ρ s is snow density and c s is the specific heat of snow (2.09 × 103 J kg− 1 K− 1). The thermal conductivity, k s, is assumed to be 0.42Wm− 1 K− 1 for snow and 2.0715 Wm− 1 K− 1 for ice (Reference OkeOke, 1987). We assume two layers for both snow and ice. The volume of snow- or icepack affected by temperature fluctuations was estimated from the amplitude of the temperature oscillations according to Reference OkeOke (1987) (see also Reference CorripioCorripio, 2003). Following Reference Greuell and KonzelmannGreuell and Konzelmann (1994), 36% of the net shortwave radiation was assumed to be absorbed by the surface layer, whereas the rest penetrates into the snowpack. The temperature of the snow-or ice-pack surface layer is computed from Equation (3), and is then used for computation of both the outgoing longwave radiation and the turbulent fluxes.
Energy available for melt is converted into millimetres water equivalent by dividing by the latent heat of fusion of water (λ = 0.334 MJ kg− 1). The model therefore needs as input data hourly measurements of incoming shortwave radiation (Wm − 2), reflected shortwave radiation (Wm − 2), air temperature ( ˚ C), air vapour pressure (Pa) and wind speed (m s − 1). It is run at hourly resolution and computes hourly melt rates.
3.2. Model application
At all locations we applied both the model which includes Q S (henceforth referred to as EBSSF), and the version without subsurface heat flux (henceforth referred to simply as EB). In the latter case, the surface temperature is assumed to be 0 ˚ C, and the outgoing longwave radiation, L↑=σT 4 (with σ being the Stefan–Boltzmann constant, equal to 5.67 × 10 − 8Wm− 2 K − 4), is equal to the constant value of −316Wm − 2 (Reference OkeOke, 1987). The model was run at all locations for the entire period of functioning of the AWSs.
4. Results and Discussion
4.1. Testing the zero-degree assumption across Haut Glacier d’Arolla in the 2001 ablation season
Table 3 shows the total melt computed with and without inclusion of the subsurface flux at the five Haut Glacier d’Arolla sites in 2001. The period of functioning of the five AWSs is
Table 3. Total melt computed by the energy-balance model with (EBSSF) and without (EB) inclusion of the heat-conduction flux at the five AWS sites on Haut Glacier d’Arolla in 2001 for the entire ablation season (30 May to 11 September 2001). The difference is computed as EB − EBSSF and expressed as the percentage over the total melt computed by EB
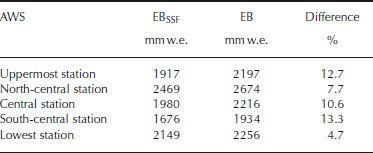
the same (except for gaps at the north-central, central and lowest station (see Table 2)), from 30 May to 11 September 2001. Differences range from 4.7% to 13.3% at the five sites. The maximum difference in total melt computed by the two model versions is at the south-central station (13.3%), followed by the uppermost station (12.7%). The minimum difference is at the lowest station (4.7%). A clear pattern emerges from these values: the largest difference between the two model versions is at the AWS sites in the accumulation area, which are covered by snow for the entire season, while the smallest differences are at the stations in the ablation area, where the higher air temperature ensures that the snowpack is warmer and where ice is exposed for longer periods. Snow has stronger insulating properties and a lower thermal conductivity than ice (Reference OkeOke, 1987), and the temperature of snow covers on glaciers can be below zero for several tens of centimetres and more (e.g. Reference Wagnon, Ribstein, Kaser and BertonWagnon and others, 1999). On temperate glaciers, conversely, only an upper thin layer of ice can be at temperatures below zero (Reference HockHock, 2005).
Higher melt is computed by EB also at the beginning and at the end of the ablation season, when the glacier is covered by a deep layer of snow due to the winter accumulation or to the new snowfalls, as is evident from Table 4. In the days from 31 August to 11 September intense snowfalls covered the entire glacier with a snow layer that shut down the melt process. Their effect is seen at both the south-central and central stations, where the difference in total melt predicted by the two model versions is high, as it was at the beginning of the season (Table 4). Differences between the two models are similar for the whole period except the last part of the season. In August, total melt simulated by both model versions at the two locations diverges because of the higher energy receipt at the central station compared to the south-central, associated with the topographic characteristics of the two sites (Reference Pellicciotti, Brock, Strasser, Burlando, Funk and CorripioPellicciotti and others, 2005). In the period 16–31 August, when snow is depleted at the central site but not at the south-central, a difference is evident: total melt (simulated by both models) is much higher at the central site because ice has lower albedo and thus absorbs more shortwave radiation. The difference between the two model versions with and without heat conduction becomes significantly higher at the snow-covered site (9.4% cf. 2.2%), confirming that the loss of energy by subsurface flux is a more important process on snow than on ice (Table 4). Although not reported here, the same pattern of differences between the two model versions during the season was observed at all five sites.
Table 4. Total melt computed by the energy-balance model with (EBSSF) and without (EB) inclusion of the subsurface flux for sub-periods of the ablation season at Haut Glacier d’Arolla south-central and central stations in 2001. The difference is computed as EB − EBSSF and expressed as the percentage over the melt computed by EB
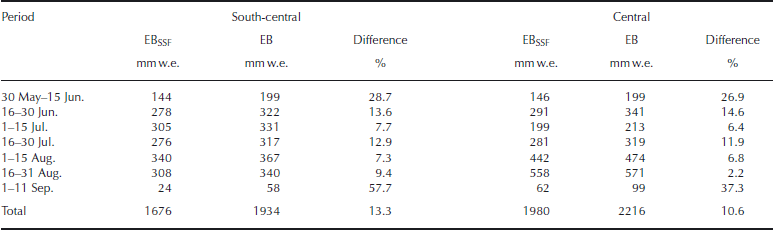
Figure 1 shows that the differences in total (and daily) melt originate from overestimation of melt by EB in the first morning hours; this was also demonstrated by Reference PellicciottiPellicciotti and others (in press) at the same site in the dry Andes investigated in this study. On ice (at the lowest station) there is no delay between melt simulated by the two models, whereas on snow (uppermost station), assuming that the surface is always at zero degrees results in an earlier melt, since energy is first used to heat the snowpack to melting point before melt can occur. This effect is stronger on days with lower night temperatures such as 21–23 August (Fig. 1). On 3 and 4 September, little or no melt occurs because of the heavy snowfalls.

Fig. 1. The hourly air temperature measured at the two AWSs. (b, c) Hourly melt rates simulated by EB and EBSSF at Haut Glacier d’Arolla uppermost (b) and lowest (c) stations in the 2001 ablation season.
4.2. Testing the zero-degree assumption across glaciers and seasons
Results from the two model runs at all other sites are shown in Table 5. Differences between the model with and without the heat-conduction flux are rather small, except for Tsa de Tsan glacier (10.4%). All other differences range from 0.5% (Glaciar Juncal Norte) to 2.8% (Gornergletscher 2005). The lowest differences are typical of sites where ice was exposed for a longer period, with the smallest differences between the two model versions being at Juncal Norte (56.3% of days with ice exposed) and Haut Glacier d’Arolla 2005 (0.8% difference with 75% of days with ice exposed). The largest difference is at the AWS of Tsa de Tsan glacier (9.1% of ice days) (Table 6). There is a clear correlation between surface characteristics and the importance of the heat-conduction flux, as for ice-covered sites (or sites where ice is predominant) the heat-conduction flux becomes negligible, whereas ignoring it results in large differences in total melt at snow-covered sites (or sites covered by snow for most of the time). This confirms the finding of the analysis at the five Haut Glacier d’Arolla sites reported above.
Table 5. Total melt computed by the energy-balance model with (EBSSF) and without (EB) inclusion of the heat-conduction flux at all sites considered in this work, except the five AWS sites on Haut Glacier d’Arolla in 2001. Totals are computed at each site for the entire ablation season (see Table 2). Difference is computed as EB − EBSSF and expressed as a percentage over the total melt computed by EB
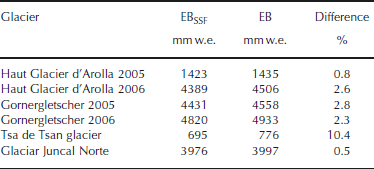
Table 6. Main meteorological conditions and surface characteristics of the AWS locations at the four study sites. HGdA indicates the lowest station on Haut Glacier d’Arolla, and Gorner indicates Gornergletscher. T is air temperature
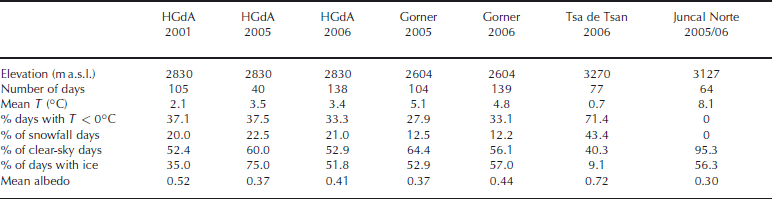
With the exception of Tsa de Tsan glacier, the values in Table 5 are lower than those found at the five sites on Haut Glacier d’Arolla in 2001 (Table 3), in particular the values at the lowest station, where we found a difference of 4.7% in 2001, of 0.8% in 2005 and of 2.6% in 2006. Also taking into account that the three seasons have different durations (Table 2) and that distinct surface characteristics play a role, as discussed above, air temperatures in 2001 were lower than for the other sites and seasons (Table 6), with the exception of Tsa de Tsan glacier, where mean air temperature over the period 26 July to 30 September was 0.7 ˚ C. The mean value at Haut Glacier d’Arolla lowest station in 2001 was 2.1 ˚ C, compared to mean values of 3.5 and 3.4 ˚ C in 2005 and 2006, respectively (Table 6). Reference Greuell and SmeetsGreuell and Smeets (2001) analyzed the impact of the zero-degree assumption on the glacier energy balance at five locations on Pasterze glacier, Austria. They found that computation with and without the subsurface module gave almost the same results because of the high temperature during their study. At the two sites with elevations of 2945 and 3225 ma.s.l. (comparable to the range of elevations of the AWSs in this paper), mean temperatures were 3.5 and 3.2 ˚ C, respectively, similar to our values at Haut Glacier d’Arolla lowest station in 2005 and 2006.
Since the sites have different characteristics in terms of topography, surface properties, elevation and meteorological conditions, we looked at the difference in total melt simulated by the two models as a function of the sites’ mean temperature over the season. This can be regarded as an integrated index of total energy (Reference OhmuraOhmura, 2001), and is implicitly
a surrogate for elevation, as higher-elevation sites typically have lower temperatures. A clear relationship between mean seasonal temperature and the influence of heat-conduction flux exists at all sites: differences between EB and EBSSF are higher at lower temperatures (in general corresponding to higher-elevation sites), where the zero-degree assumption does not hold, and decrease with increasing mean temperature (Fig. 2). The value in the bottom right corner of Figure 2 corresponds to the Glaciar Juncal Norte site, characterized by very high air temperatures (Table 6).

Fig. 2. Difference in total melt at the end of the season computed by EB (M EB) and EBSSF (M EBSSF) versus mean temperature over the season for all sites investigated. The difference is expressed as % over the total simulated by EB.
A striking result is the small difference in model performance between EB and EBSSF at the AWS on Glaciar Juncal Norte (0.5%), which indicates that the subsurface flux accounts for only a small percentage of the total energy balance. A similar result was obtained by Reference PellicciottiPellicciotti and others (in press) using a different energy-balance model (Reference CorripioCorripio, 2003). On Juncal Norte we would have expected the cooling of the snowpack and surface ice to be particularly effective because of the very dry atmosphere, with clouds practically absent and, therefore, reduced incoming long-wave radiation. At our site, however, this effect is compensated for by the high energy receipt that reaches the surface in the daytime, due to the extremely high solar radiation (Reference PellicciottiPellicciotti and others, in press) and very high air temperature (Fig. 3; Table 6). Air temperatures were never below zero, in contrast to the seasonal pattern of air temperature at Haut Glacier d’Arolla lowest station, where temperatures drop below zero in the middle of the ablation season (around mid-August) (Fig. 3). Radiative cooling does occur at Juncal Norte AWS, as demonstrated by the drops of surface temperature evident at night in the first half of the ablation season until about 14 January, when the surface turns into ice (Fig. 3). The surface, however, is heated very quickly because of the strong energy input available once the sun rises (high air temperature and intense solar radiation), and therefore only a very small loss of melt energy results from the night cooling of the snow surface. Reference PellicciottiPellicciotti and others (in press) also showed that the delay in the onset of melt when subsurface conductive fluxes are neglected was small and had little influence on the total melt predicted by the model at the end of the season.

Fig. 3. Comparison of 2 m air temperature measured at the AWS and surface temperature simulated by EBSSF atGlaciar Juncal Norte AWS (2005/06) and at the Haut Glacier d’Arolla lowest station (2006). (The horizontal lines indicate a temperature of 0 ° C.)
A clear correspondence between air and surface temperature can be observed at both sites, with lower surface temperatures corresponding to lower air temperatures (and snow on the surface) (Fig. 3).
4.3. Comparison of measured and simulated surface temperature
A common way of validating melt models is to compare the total melt simulated by the model with readings from ultrasonic depth gauges (UDGs). These readings, however, can be affected by large errors (Reference Carenzo, Pellicciotti, Rimkus and BurlandoCarenzo and others, in press). In this work we focus on a comparison of two energy-balance models that differ only in the inclusion of the heat-conduction flux and recomputation of the surface temperature. We are therefore interested in testing first of all the assumption that the glacier surface was always at zero degrees. We compared surface temperature simulated by EBSSF with hourly observations measured for the whole ablation season at Haut Glacier d’Arolla lowest station in 2006. The comparison is shown in Figure 4 for the entire season and for the period 28 May to 27 June. The overall agreement is very good, and the model is able to reproduce closely the sub-daily variations in surface temperature (Fig. 4), with both some under- and overestimations. The model simulates lower than observed temperatures during the transition from snow to ice (such as in the first days of August). It also has to be taken into account that the sensor has an accuracy of ±0.5 ° C at 0 ° C, and of ±1.5 ° C at −10 ° C, so part of the differences in Figure 4 may be caused by the sensor accuracy (as well as the measurement accuracy that we cannot evaluate precisely). The periods when the glacier is covered by snow are evident in Figure 4, and correspond to the lower temperature values, in agreement with theory (e.g. Reference HockHock, 2005). The model does well both on snow and ice. We are therefore confident that the model correctly simulates the exchange of heat within the glacier snow and ice.

Fig. 4. Comparison of measured and simulated surface temperature at Haut Glacier d’Arolla lowest station in 2006 for the entire ablation season (top) and for the snow-covered period, 28 May to 27 June (bottom). Simulated temperature is obtained with EBSSF.
4.4. Model experiment: extrapolation to higher elevations
A limitation of this work is that no AWSs were available at high elevations. Our highest location was the AWS on Tsa de Tsan glacier at 3250 ma.s.l., followed by the Glaciar Juncal Norte AWS at 3127 ma.s.l. and by Haut Glacier d’Arolla uppermost station at 3015 ma.s.l. From the analysis of the differences in model performance at all sites, it emerges clearly that the highest sites are those where it is most likely that the zero-degree assumption does not hold. At these sites, neglecting the subsurface heat flux into the snow or ice leads to a consistent overestimation of melt, because of a combination of various factors: the glacier surface is covered for longer period (or for the entire ablation season, as at Haut Glacier d’Arolla uppermost station in 2001) by snow, which is a better insulator than ice and where the cooling at night can be important; albedo is higher, thus reducing the absorption of incoming shortwave radiation (Reference Greuell and SmeetsGreuell and Smeets, 2001) and air temperatures are lower. On a small valley glacier such as Haut Glacier d’Arolla our AWSs are representative of the spatial variability in the upper basin and accumulation area of the glacier, since only the steep lateral ice-falls extend up to 3500ma.s.l. Larger glacier systems such as Gornergletscher, conversely, have a much greater elevation range (Table 1). In order to assess the overestimation of total melt that results from the zero-degree assumption at altitudes higher than those covered by our AWSs, we have run both models at a hypothetical location 4000ma.s.l. on Gornergletscher, assuming that the surface is always covered by snow (z 0 = 1 mm). Air temperature was extrapolated from the values at Gornergletscher AWS (2604 ma.s.l.) using the atmospheric lapse rate of −0.0065 ˚ Cm − 1. We assume that all other meteorological input data to the energy-balance model (wind speed, relative humidity and incoming solar radiation) stayed the same as at the Gornergletscher AWS in 2006, but have used a constant albedo of 0.65, which is the mean value observed at the AWS for the snow-covered period. In this way, we are ruling out the possibility that new snowfalls reset the albedo to its highest values (≥0.8), thus covering the glacier with a layer of very high reflectivity. In this case, the snow-cover temperature would probably be even lower. We obtain a total melt at the end of the season of 1411 mmw.e. with EB, and 1044 mmw.e. with EBSSF, corresponding to a difference of 26%. This is a high value that cannot be neglected in the estimation of the total melt and thus the mass balance of a glacier, and points to the importance of including the heat-conduction flux in distributed energy-balance models of large glacier systems.
5. Concluding Remarks
In this paper, we have quantified the difference in total melt that results from energy-balance calculations which do not take the heat-conduction flux into glacier snow and ice into account at different sites on three alpine and one andean glacier. This difference ranges from <1% for warm periods of ongoing melt at ablation area sites to ∼14% for cold periods with frequent snowfalls at snow-covered locations. For locations in the accumulation area of alpine glaciers such differences might not be negligible.
We have also looked at the variations in model performances within one ablation season at different sites across one alpine glacier (Haut Glacier d’Arolla), and found that if the cold content of the snowpack at the beginning and end of the ablation season is not taken into account this leads to an overestimation of melt of ∼30% and up to 50%, respectively. The latter value (beginning of September 2001) is associated with the first fresh snowfalls. Our results also indicate that the same is true for cold periods within the ablation seasons, as in the case of the second half of July at the Haut Glacier d’Arolla 2001 sites. We have demonstrated that the overestimation by the model with the zero-degree assumption originates from a too early prediction of morning-hours melt, when energy that is in reality used to raise the snow temperature to melting point is directed to melt by the model.
We have also shown that a clear inverse relationship exists between the difference in total melt at the end of the ablation season and the mean air temperature over the season across several glacier sites and years: larger overestimation by the model that assumes the surface to be at zero degrees is obtained for lower air temperatures. In these conditions, the snowpack needs to be heated to melting point to compensate for radiative cooling more than in sustained periods of high energy inputs (such as in the middle of the melt season). This relationship could be employed for a first estimation of the melt overestimation by the zero-degree assumption for sites at high elevations or where measurements are not available, especially for distributed modelling. An experiment to assess the impact of the zero-degree assumption at higher sites has indicated that at an elevation of 4000 ma.s.l. on Gornergletscher the overestimation of melt could be substantial, as high as a few tens of per cent.
On Glaciar Juncal Norte, in the dry Andes of central Chile, we would have expected the strong radiative cooling due to the dry atmosphere to cause an increase of the cold content of the snowpack. This, however, seems to be compensated by the high energy input that reaches the surface in the daytime and by the high air temperatures (always above zero degrees), at least at the location of our AWS (3127ma.s.l.). It thus offers a distinct picture from that which we found for the locations in the Alps. At the Glaciar Juncal Norte site, the difference between the two model versions was the smallest of all sites and seasons considered (0.5% over 64 days).
Our results agree with the findings of the few studies where the influence of the zero-degree assumption has been clearly tackled (e.g. Reference Greuell and SmeetsGreuell and Smeets, 2001; Reference PellicciottiPellicciotti and others, in press). Future work could be devoted to separating the effect of the surface properties (snow and ice) from that of the meteorological conditions determining the overestimation by the zero-degree assumption of daily and total melt, and to quantifying separately the impact of these two factors on the differences we have found.
Acknowledgements
We thank E. Cremonese and U. Morra di Cella (ARPA Valle d’Aosta, Italy) for collecting the meteorological data on Tsa de Tsan glacier in a joint campaign with the Federal Institute of Technology (ETH) Zürich, and A. Kretz for participating in the 2006 field campaign on Gornergletscher. R. Dadić provided the surface-temperature data on Haut Glacier d’Arolla in 2006. The scientific editor G. Cogley, R. Braithwaite and an anonymous reviewer provided constructive comments on an earlier version of the manuscript.












