1. Introduction
Because data from the surface of a glacier can, in general, be obtained much more easily than data about basal conditions, it is of interest to be able to predict basal variables such as bedrock profile and basal slipperiness using surface data only. The first step towards this goal involves understanding how basal variability affects the surface geometry and surface velocities, and determining theoretically the transfer of basal variability towards the glacier surface. Various attempts have been made towards this end. A recently developed perturbation analysis of the transmission of basal variability to glacier surfaces (Gudmundsson, in press) predicts that the surface-to-bedrock amplitude ratio is strongly affected by the ratio between mean basal sliding velocity and mean forward deformational velocity (slip ratio). A similar effect of the slip ratio on the transmission of bedrock undulations towards the surface is not expected, on the basis of some commonly used theories of glacier flow such as the zeroth-order shallow-ice approximation or the traditional kinematic wave theory.
Obtaining observational data on how bedrock-to-surface amplitude transfer is related to slip ratio is complicated by the fact that the amplitude ratio depends on a number of other factors beside the slip ratio, such as the rheological properties of the ice, spatial extent of the basal perturbations, and average surface slope. A situation where the slip ratio changes suddenly, while all other relevant factors remain the same, would clearly be ideal. The transition to surging provides an excellent example of these conditions. In a surge, the basal sliding velocities are an order of magnitude larger than during the quiescent periods prior to and after the surge. At the same time, other factors affecting the transmission of basal variability towards the surface remain more or less the same. Observing changes in basal transfer towards the surface during a surge thus allows theoretical concepts about the relationship between bed and surface to be tested.
Here we describe observations of changes in surface shape made on Tungnaárjökull, Vatnajökull ice cap, Iceland, prior to and during a major surge in 1994. We show that the surface-to-bedrock amplitude ratio increased significantly during the surge in agreement with predictions based on first-order perturbation analysis. This increase is not predicted by the zeroth-order shallow-ice approximation.
2. Theory
The effects of spatial variations in basal geometry on the surface of glaciers can be determined analytically using perturbation methods. Various authors have used this approach (Reference HutterHutter, 1980, Reference Hutter1983; Reference BaliseBalise, 1987; Reference ReehReeh, 1987; Reference JόhannessonJόhannesson, 1992; Gudmundsson, in press), each one extending and correcting certain aspects of previous work. The perturbation analyses by these authors lead to analytical expressions for the variations in flow set up by small-amplitude basal disturbances.The non-dimensional amplitude perturbation parameter (°) which enters these solutions is the ratio of bedrock amplitude (a) and local mean ice thickness (h), that is ∊ = a/h. No assumptions need be made about the size of the shallowness parameter (δ = h/l), where h is a typical ice thickness and l the glacier width, in contrast to the shallow-ice approximation where this parameter must be small. The solutions are thus valid over both long and short spatial scales compared with the mean ice thickness. For this reason, this perturbation theory will be called “arbitrary-wavelength theory”, whereas the shallow-ice approximation would be an example of a “long-wavelength theory”. The arbitrary-wavelength theory is first-order in the amplitude parameter, and in this approximation the theory is linear. The theory can only be used for distances over which changes in ice thicknesses are small as compared to the mean ice thickness of the area in question. The shallow-ice approximation is the limit as δ → 0 and is a non-linear theory. It can be linearized by considering small amplitude variations in bedrock (Reference Fowler and LarsonFowler and Larson, 1978; Reference FowlerFowler, 1982; Gudmundsson, in press). The resulting linear version of the shallow-ice approximation is commonly known as the traditional (linear) kinematic wave theory (Reference NyeNye, 1963).
The solutions utilized here are based on the work of Gudmundsson (in press) and are valid for a linearly viscous medium. Despite being limited to small amplitudes and linearly viscous media, the solutions are quite general in several important aspects. Both horizontal stress gradients, ignored in most shallow-ice models, and shearing through the ice column, ignored in ice-shelf models, are, for example, fully accounted for. The non-linear problem has been investigated by Reference Landon and RaymondLandon and Raymond (1978), Reference BaliseBalise (1987) and Reference JόhannessonJόhannesson (1992).
The steady-state bed-to-surface amplitude transfer is predicted to be a fairly complicated function of wavelength (A), orientation of the wave crest with respect to mean flow direction (0), and mean surface slope (σ) (Gudmundsson, in press). A key variable affecting the bed-to-surface amplitude transfer is the slip ratio ( C (0) ) , defined as the ratio between basal sliding velocity (ub) and mean deformational velocity (ud). The upper part of Figure 1 shows the transfer amplitude of the surface with respect to the bed profile as a function of wavelength, for sinusoidal bed undulations according to the analysis by Gudmundsson (in press). The analytical expression for the transfer function is given in the Appendix. The crests of the sinusoidal bed profile are transverse to the mean flow direction. The figure shows that with increasing slip ratio (C(0)) the transfer amplitude increases significantly over a fairly wide range of wavelengths. The qualitative features of the amplitude ratio also change as the slip ratio is increased, with a local maximum in transfer amplitude being formed at wavelengths around 5–15 times the mean ice thickness (h (0) ). This maximum becomes broader and shifts to larger wavelengths as the slip ratio becomes larger. At slip ratios larger than 100, the transfer amplitude is almost equal to unity at wavelengths around 10 times the mean ice thickness, and larger than 0.5 at all wavelengths larger than about 2.5h(0).

Fig. 1. bed-to-surface amplitude transfer of a sinusoidal bedrock undulation and relative phase shift between surface and bed as a function of wavelength for a number of different slip ratios (c(0)). the crests of the sinusoidal bedrock undulations are normal to the mean direction of flow. mean surface slope is equal to 1˚.
The relative position of the sinusoidal surface wave with respect to the bed wave is also strongly dependent on C(0) (lower part of Fig. 1). For C(0) = 1 the phase shift is close to -π/2˚ for wavelengths within the range 2 – 5 0 h (0) . For a phase shift of -π/2˚ , the peak of the sinusoidal surface wave is upstream of the corresponding peak of the bed profile, with the inflection point of the sinusoidal surface profile directly above the peak of the bed profile. As C(0) increases, the phase shift becomes smaller in magnitude and the surface wave more in phase with the bed wave. In the limiting case of C (0) → +∞ the surface is exactly in phase with the bed (Gudmundsson, in press).
Providing that factors such as mean surface slope and ice viscosity do not change, an increase in slip ratio leads to an increase in bed-to-surface amplitude transfer and a downstream shift in the location of surface crests. The predicted increase in transfer amplitude is large. For a change in slip ratio from unity to 4 100, the transfer amplitude increases from about 0.1 to 4 0.8 over wavelengths ranging from 3 to about 20 times the mean ice thicknesses (Fig. 1).
A similar increase in amplitude transfer is not caused by a spatial variation in basal lubrication. The corresponding transfer amplitude and phase shift are shown in Figure 2. A spatial variation in bed lubrication is here defined as a spatial variation in the parameter c entering a basal sliding law of the type ub = cτb, where ub is the basal sliding velocity, τb the basal shear stress, and c the basal lubrication. Figure 2 is based on the results of a perturbation analysis, and the details can be found in Gudmundsson (in press). The equations used here are listed in the Appendix. It is not possible to give a physical meaning to the numerical values of the transfer amplitudes in the figure without explaining how variables have been scaled. The important aspects of Figure 2 are the small relative changes in transfer amplitudes with increasing slip ratio compared with those in Figure 1, and the fact that amplitudes increase monotonically as a function of wavelength (Fig. 2), without forming a local maximum of the type seen in Figure 1.

Fig. 2. bed-to-surface amplitude transfer of a sinusoidal variation in basal slipperiness and relative phase shifts. basal slipperiness is defined as the constant c in the sliding law ub = Cτb, where ub is the sliding velocity and τb the basal shear stress. the transfer amplitude corresponds to the amplitude of a sinusoidal surface undulation, as a fraction of mean thickness (d), caused by a basal slipperiness perturbation having an amplitude equal to d/(2η), where η is ice viscosity.
The relative phase shifts between surface and bed undulations (lower half of Fig. 1), on the one hand, and surface undulations and basal slipperiness variations (lower half of Fig. 2), on the other, differ by exactly 180° for all wavelengths. This difference is a simple consequence of the fact that a positive perturbation in basal slipperiness will lead to an increase in basal velocities, whereas a positive bedrock undulation (bump) causes a corresponding reduction. For large slip ratios, the surface lowering associated with a localized (positive) slipperiness perturbation is almost directly above the maximum increase in basal slipperiness.
Summarizing, the amplitude ratio between surface and bed undulations is strongly dependent on the ratio between mean sliding and mean deformational velocities. As the sliding increases, keeping other factors constant, the amplitude-ratio curve has a local maximum as a function of wavelength.The amplitude ratio increases by roughly a factor of 5–10 as the slip ratio changes from unity to about 100–200 (Fig. 1). Spatial variations in basal lubrication do not give rise to a similar increase in transfer amplitudes (Fig. 2).
3. Study Area
Tungnaárjökull is an outlet glacier of Vatnajökull ice cap, Iceland, flowing towards the southwest (Fig. 3). Like most of the other major outlet glaciers of Vatnajökull, Tungnaárjökull has a history of surges. Because the glacier is located far away from any settlements, there are no records of any surges before the start of the 20th century. Tungnaárjökull surged around 1920, again in 1945, and the latest surge took place in 1994 (Reference Björnsson, Pálsson, Sigurðsson and FlowersBjörnsson and others, 2003). In 1992 Köldukvíslarjökull, north of Tungnaárjökull, started surging, and the 1994 surge of Tungnaárjökull may possibly have been related to the surge of Köldukvíslarjökull. Síðujökull, south of Tungnaárjökull, also surged in 1994 and by then the whole western side of Vatnajökull was surging.

Fig. 3. Location map. North points upwards. The line running down Tungnaárjökull shows the location of the profile Figure 4.
3.1. Surface velocities
Annual surface velocity measurements have been conducted on Tungnaárjökull since 1992. Prior to the start of these systematic velocity studies, sporadic measurements of surface velocities were made. For example, the summer velocities in 1986, well ahead of the start of the 1994 surge, are known. The velocity data from 1992 to 1993 show seasonal variations in surface velocities, which are then followed by a slow increase in velocity during winter 1993/94, and a much more rapid increase in summer 1994. From November 1994 until September 1995 it was not possible to measure surface velocities, and by then the surge had ceased. It is thus not accurately known when the maximum surge velocity occurred, but it is believed that the surge started to slow down shortly after November 1994.
The increase in surface velocities during a surge is known to be caused by an increase in basal motion. The slip ratio is thus larger during a surge than before the surge started. A lower estimate of the mean annual slip ratio prior to the 1994 surge can be obtained by assuming that the lowest measured velocity at each location is equal to the maximum deformation velocity. This gives slip ratios in the range 0.3–2, or on the order of unity. In November 1994, velocities were about two orders of magnitude larger than prior to the surge. Around the equilibrium line, a lower estimate for the slip ratio is in the range 100–200. The slip ratio varies somewhat with location, possibly decreasing to 50–100 up-glacier towards the ice divide.
4. Topography Changes
The surface and bedrock topography were surveyed by radio-echo soundings in 1981 (Reference BjörnssonBjörnsson, 1988). Surface altitude and ice thicknesses were thus known in some detail before the beginning of the surge. A surface and bedrock profile approximately along a flowline, based on the data collected in 1981, is shown in Figure 4. It can be seen that the ice flows over two prominent bedrock ridges (x coordinates 4000 and 14 000 in Fig. 4). Both of these ridges run approximately north-northwest, and, where the ice flows over them, the direction of the mean velocity field deviates by about 20° from being normal to the orientation of the ridges.

Fig. 4. Surface and bedrock profile along a flowline on Tungnaájökull.The location of the profile can be seen in Figure 3
The lower subglacier ridge, i.e. the ridge closer to the terminus (x coordinates 4000 in Fig. 4), is approximately 130 m high and about 2 km wide at the base. The ice thickness is 300 m upstream from the ridge, but only about 100 m directly above it. The surface profile seen in Figure 4 is clearly affected by the presence of the subglacier ridge. By subtracting a mean slope over a distance of some 10 km from the surface profile in Figure 4, the predominant wavelength and amplitude of the disturbance in surface geometry can be estimated. The surface disturbance is wavelike, although not strictly sinusoidal, with a wavelength of about 3.5 km, amplitude of 30 m, and relative phase shift with respect to the bedrock ridge of about–45°. The amplitude ratio is thus around 0.23, and the wavelengths in the range 5–50. This amplitude ratio is rather large, but, as the following discussion depends on the approximate range rather than exact values of theoretically predicted transfer amplitudes, this does not pose a problem.
The upper ridge (x coordinates 14 000 in Fig. 4) is approximately 200 m high and 2.5 km wide at the base. The ice thickness is 700 m upstream from the ridge and 350 m above the ridge. The associated standing surface wave is about 20–40 m high, 3.5 km long and has approximately – 90° phase shift relative to the bedrock ridge. The wavelength is thus approximately 6 and the amplitude ratio around 0.1–0.2.
It was not possible to survey changes in the surface topography during the surge. However, by comparing oblique photos of the area taken prior to and during the surge from a similar viewpoint (Figs 5 and 6), it nevertheless becomes clear that the surface shape changed significantly in the course of the surge. The surface lowered by about 100 m in the accumulation area while the terminus advanced by about 1 km. In addition to these large-scale changes in ice-thickness distribution, the surface profile in the vicinities of the two ridges changed markedly. The surface undulations seen in Figure 6 are not related to a propagation of a surge front. At the time picture 6 was taken, the surge front had reached the terminus, and all of the area of Tungnaárjökull seen in the picture was surging.

Fig. 5. Tungnaárjökull before the 1994 surge started. The view towards north with the flow direction approximately from right to left (photo H. Björnsson 1993).

Fig. 6. Same view as in Figure 5 during the surge (photo H. Björnsson 1994).
During the surge, two large surface ridges were formed (Figs 6 and 7). The exact locations of these surface ridges in relation to features of the bedrock are difficult to determine. Nevertheless, it is clear that each surface ridge lies within a few hundred meters of one of the bedrock ridges. The development of the surface geometry with time could not be followed in detail, but it seems likely that in the course of the surge these large surface ridges grew gradually from the much smaller surface undulations seen in Figure 4. The increase in amplitude of the surface disturbances around the bedrock ridges indicates that the amplitude ratios between surface and bedrock increased significantly after the onset of the surge. A Fourier decomposition of bed and surface profile would be needed to give an exact estimate of the changes in amplitude ratios as a function of wavelength. Because sufficiently good surface data for this purpose are not available, only rough estimates of changes in amplitude ratios can be made. In view of the large changes in surface geometry associated with the surge, this does, however, not pose a significant problem. From the length of the shadows cast by the surface ridges, the amplitude of the lower surface ridge is estimated to be 100 ±25 m. Thus, the amplitude ratio clearly increased substantially, from about 0.23 prior to the surge to about 0.6–0.8 during the surge. A similar increase in amplitude ratio is found for the ridge further up-glacier. After the surge, the amplitude of both of these surface ridges reduced to values similar to those observed before the start of the surge.

Fig. 7. View of the terminus during the surge (photo H. Björnsson 1994).
5. Discussion and Conclusions
The 1994 surge of Tungnaárjökull led to an increase in slip ratio from about unity to several hundred. At the same time, the surface became more undulating. The surface-to-bed amplitude ratios changed from about 0.1 to about 0.7. These values are not exact, and the changes in amplitude ratios as a function of wavelength cannot be estimated. Nevertheless, this increase is both large and real.
Figure 1 shows that an increase in slip ratio from 1to 100 is predicted to cause the bedrock-to-surface transfer amplitude to change from 0.1 to about 0.7 over a large range of wavelengths. This corresponds well with the observed changes in amplitude ratios. This change in amplitude ratios can, on the other hand, not be explained as a consequence of changes in the degree of basal lubrication. As Figure 2 shows, the corresponding effects on surface amplitudes are too small. It is, however, conceivable that large-amplitude changes in lubrication might affect the surface more strongly than the linearized theory used here predicts.
The amplitude transfer of bedrock undulations towards the surface can also be calculated using the traditional kinematic wave theory. As described above, the traditional kinematic wave theory can be obtained by linearizing the shallow-ice approximation (SIA) which is an example of a long-wavelength theory. Since the SIA is commonly used to describe the flow mechanics of glaciers and ice sheets, it is of interest to see how well the SIA predicts the observed increase in transfer amplitudes during the surge. Figure 8 shows transfer amplitudes and phase shifts calculated using both the arbitrary-wavelength theory (thick lines) and the (linearized) long-wavelength theory (thin lines), for two different slip ratios. At a slip ratio of one, the transfer amplitudes calculated with these two theories do not differ significantly, and the phase shifts are similar for all but the shortest wavelengths. Calculating surface shapes from known bedrock profiles for the quiescent periods prior to and after the active surge phase using both theories would thus lead to similarly shaped surface profiles. At a slip ratio of 200 there are, on the other hand, significant differences in calculated transfer amplitudes and phase shifts (Fig. 8). The long-wavelength theory does not produce the observed increase in transfer amplitudes associated with the surge. The arbitrary-wavelength theory used here, though limited to linear media, gives a much better description of the relationship between bedrock and surface than commonly used theories of glacier flow such as the zeroth-order shallow-ice approximation and the traditional kinematic wave theory. Only rough estimates of transfer amplitudes are needed to demonstrate this.

Fig. 8. Transfer amplitudes and phase shifts calculated with two different perturbation schemes valid for waves of arbitrary wavelengths (thick lines) and long waves (thin lines).
The arbitrary- and long-wavelength theories differ in their treatment of horizontal deviatoric stresses. In the zeroth-order SIA the horizontal deviatoric stresses are ignored. The traditional kinematic wave theory is a linearized version of the zeroth-order SIA and, as does the SIA, predicts the flux of ice to be a local function of slope and thickness.With increasing slip ratio, the transmission of horizontal stresses becomes increasingly important and the flow can no longer be predicted on the basis of local slope and thickness only. For a slip ratio of 0–5, the differences in theoretically calculated transfer amplitudes are relatively small, as can be seen from Figure 8. As the slip ratio increases, these differences, however, become quite significant both numerically and qualitatively. The strong increase in transfer amplitude observed in the surge of Tungnaárjökull reveals a non-local aspect of glacier mechanics which has not been previously shown to exist.
Acknowledgements
We acknowledge the logistical support of the Glaciology Society of Iceland (JÖRFÍ) during the fieldwork. This work was supported by the National Power Company (Landsvirkjun). We thank W. F. Budd and an anonymous reviewer for careful reviews of the present paper. We thank R. C. A. Hindmarsh, A. Jenkins and D. Vaughan for many helpful comments.
Appendix
Transfer Functions
The transfer functions used in the text to calculate the response of the surface geometry (s) to perturbations in bed geometry (b) and basal slipperiness (c) are given by
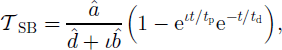
and
where ι is the imaginary unit, kx and ky are the longitudinal and the transverse wavenumbers, respectively, and k is defined as
![]() The wavenumbers are dimensionless as all spatial distances have been scaled with the mean ice thickness. The sb transfer function is inherently dimensionless and its modulus is the amplitude ratio between surface and bed. The modulus of the sc transfer function is the ratio between (scaled) perturbed surface amplitude (ΔS) and the fractional perturbation (Δc) in basal slipperiness (c), that is,
The wavenumbers are dimensionless as all spatial distances have been scaled with the mean ice thickness. The sb transfer function is inherently dimensionless and its modulus is the amplitude ratio between surface and bed. The modulus of the sc transfer function is the ratio between (scaled) perturbed surface amplitude (ΔS) and the fractional perturbation (Δc) in basal slipperiness (c), that is,
whereas basal slipperiness is the ratio between basal sliding velocity (ub) and basal shear stress (τb ). The perturbation in basal slipperiness (Δc) is defined through
where
![]() is the mean (dimensional) basal slipperiness.
is the mean (dimensional) basal slipperiness.
The following abbreviations have been used:

and
The constant c( 0) is the mean (non-dimensional) basal slipperiness. In dimensional form, the sliding law is ub = cτb, where c is the dimensional basal slipperiness, which is related to its dimensionless counterpart through c = 2ηc/d(0), where η is the ice viscosity and d( 0) the mean ice thickness. The expressions above have previously been listed in Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others (1998), but the expression for ĉ in Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others (1998) contains a typing error. The first author thanks C. Schoof at Oxford University for spotting this mistake.
The two time-scales t d and tp, referred to as the diffusion time-scale and the propagation time-scale, respectively, are given by
The time-scales are dimensionless, and dimensional times are obtained by multiplying by the ratio between mean ice thickness and mean deformational velocity. The duration of the surge on Tungnaárjökull was sufficiently long that only the steady-state limit of the above-listed transfer functions had to be used.










