1. Introduction

Sea ice is a porous composite of pure ice with brine, air and salt inclusions (Reference Weissenberger, Dieckmann, Gradinger and SpindlerWeeks and ackley, 1986; Reference Eicken, Thomas and DieckmannEicken, 2003). as brine, sea water or snowmelt flows through sea ice, it carries salt, heat and nutrients. upward-flowing liquid can flood the ice surface, providing an important mechanism for ice production, particularly in the antarctic (Reference Ackley, Lytle, Kuehn, Golden and DarlingAckley and others, 1995; Reference Perovich and GowMaksym and jeffries, 2001). fluid transport through sea ice also plays an important role in heat transfer between the ocean and atmosphere (Reference Maksym and JeffriesLytle and ackley, 1996; Reference Weeks, Ackley and UntersteinerTrodahl and others, 2000), and in the input of dense brine and fresh water into the upper ocean from freezing, melting and drainage processes (Reference Weissenberger, Dieckmann, Gradinger and SpindlerWeeks and ackley, 1986; Reference TorquatoThomas and dieckmann, 2003). moreover, brine transport substantially controls the replenishment of nutrients for sea-ice algal communities (Reference Golden and HornungFritsen and others, 1994; Reference Lytle and AckleyLizotte and arrigo, 1998), and it controls bacterial uptake of dissolved organic matter (Reference Lizotte and ArrigoLizotte, 2003).

While fluid transport controls a broad range of sea-ice processes, the sizes, shapes and connectivity of the brine inclusions control fluid transport. for a typical temperature range between –20˚c and –1˚c, the volume fraction δ of brine in sea ice with salinity of 5 ppt ranges between 0.9% and 24.7%. over this temperature interval, the pore microstructure ranges from small brine pockets, disconnected at all but the smallest scales, to the development of large, vertically oriented brine channels penetrating much of the ice thickness (Reference Cole and ShapiroCole and shapiro, 1998). correspondingly, the fluid permeability k(δ) of sea ice in the vertical direction varies over many orders of magnitude. however, not much is known about the function k(δ) and how it depends on the microstructural properties of sea ice.

As one facet of a combined theoretical and experimental effort to address this fundamental issue, we propose a random pipe network to model the flow of liquid through the porous microstructure of sea ice. the radii of pipes joining the nodes of the two-dimensional square lattice are chosen from distributions describing brine inclusion cross-sections (Reference Thomas and DieckmannPerovich and gow, 1996; Reference Lizotte, Thomas and DieckmannLight and others, 2003; Reference Bock and EickenBock and eicken, 2005). the equivalence of slow flow of a viscous fluid through a pipe network and the flow of electric current through a resistor network (Reference Light, Maykut and GrenfellKoplik, 1982; Reference Chayes and ChayesChayes and chayes, 1986; Reference Fritsen, Lytle, Ackley and SullivanFriedman and seaton, 1998) opens the problem to useful types of solution, analysis and generalization.we develop a fast multi-grid method to find not only the equivalent resistance of the resistor network, that is, the fluid permeability of the pipe network, but the local electric potential or fluid pressure field at the nodes of the network as well. our results lie inside recently found void upper bounds on k(δ) (golden and others, 2006), and are in rough agreement with laboratory data on k(δ). one realization of the random network of size 1024×1024 can be solved on a g5 desktop computer in less than 2 min, and a network of size 2048×2048 with the same variance in the local properties can be solved in about 6 min.

Our scheme can be directly generalized to three dimensions, and can be modified to simulate diffusion processes in the pore microstructure, or low-frequency electromagnetic wave propagation through the composite. the network model can be used to study processes on various scales. for example, rather than representing flow through individual inclusions, the pipe radii could represent effective or homogenized flow through individual crystals, each comprising some array of typical brine inclusions. in media such as sea ice with a wide range in local properties, critical path analysis (cpa), the idea that bottlenecks control bulk flow (Reference Ambegaokar, Halperin and LangerAmbegaokar and others, 1971; Reference Fritsen, Lytle, Ackley and SullivanFriedman and seaton, 1998; Reference Golden, Ackley, Lytle, Golden, Heaton, Eicken and LytleGolden and kozlov, 1999), often plays an important role in understanding transport. since we find the local fields and choose the local properties from a distribution, our model can facilitate assessment of cpa and its applicability to sea ice. also, dynamic models of microstructural evolution which depend on local fluxes in determining increments of microstructural change can be built on our model.

Network modeling or approximation is a useful approach to analyzing the behavior of fluids in porous media, or most transport phenomena in heterogeneous materials (Reference FattFatt, 1956; Reference Berkowitz and BalbergBerkowitz and balberg, 1992; Reference DullienDullien, 1992; Reference Golden, Kozlov, Berdichevsky, Jikov and PapanicolaouGolden, 1997; Reference Fritsen, Lytle, Ackley and SullivanFriedman and seaton, 1998; Reference Torquato and PhamTorquato, 2002). the only results in this direction for sea ice that we know of are found in the notable work of Reference FreitagFreitag (1999), where fluid flow in a network model of sea ice is found using a lattice-boltzmann approach. also, the percolation threshold of a network formed the basis for the work of Golden and others (1998) in explaining critical behavior of some processes in the antarctic.

2. The Network Model

We consider sea ice with brine volume fraction δ. for slow flow of the brine with viscosity η through the pore microstructure, the local velocity and pressure fields U and P in the brine phase satisfy the stokes equations,

(1)

With the no-slip condition U = 0 on the pore boundaries. under appropriate microstructural assumptions, the averaged or macroscopic fluid velocity and pressure fields u and p satisfy darcy’s law and the incompressibility condition,

(2)

Where k is the effective permeability tensor. we shall be interested in the permeability in the vertical direction k = k _zz in units of m². these macroscopic equations can be obtained through two-scale homogenization (Reference KoplikHornung, 1996; Reference Torquato and PhamTorquato, 2002), where the fast or micro-scale is homogenized while slower variations in microstructural properties are incorporated through dependence of the effective permeability tensor on position, such as with depth in the sea ice. the mathematical analogy with electricity can be elucidated by inserting darcy’s law into the incompressibility condition, and comparing with the equation for electrical conduction,

(3)

Where σ is the conductivity tensor describing the medium and δ is the electric potential. discretizing either equation on a square or cubic lattice leads to a network model equivalent to the following, although we build this model here directly.

To simulate fluid flow through the porous microstructure of sea ice, we focus on the effective fluid transport properties of the medium at a given equilibrium state, and consider an ice sample over which the microstructural properties are constant. the dimensions of the block sample are assumed to be L×D×h, where D is the vertical depth, L is the horizontal span and h, which is comparatively very small, is the horizontal thickness. the brine microstructure of the sample is approximated by a two-dimensional lattice of nodes connected by ducts that are filled with fluid. the block has a rectangular L ×D vertical cross-section, which is divided into a grid with m equally spaced sections in the horizontal direction and n equally spaced sections in the vertical direction, so that L/m = D/n = h, for some large integers m and n. the model parameter h can be viewed as the dimension of a cell in which a typical brine inclusion is contained. in this network model, h will be chosen according to the sea ice we simulate, its brine volume fraction and our computing capacities. the ducts are assumed to have circular shapes with different radii, and the flow through the medium is induced by a pressure drop p _b – p _t, where p _b and p _t are the pressures at the bottom and the top of the sea-ice sample, with the assumption that p _b > p _t so there is an upward flow in the medium. the effective permeability generated from this model will be independent of the pressure drop as long as it is small enough so the assumptions of darcy’s law and the poiseuille flow structure stated below are valid. the cross-sectional areas of the pipes chosen below generate fluid pores comparable to the brine inclusions found in young sea ice. the lattice nodes are the vertices (i,j ), 0 ≤ i ≤ m, 0 ≤ j ≤ n, of a rectangular grid, as in figure 1a. nearest neighbors are connected by vertical and horizontal ducts, with a pressure pi,j defined at each node (i,j ). to each node (i,j ) with 0 ≤ i ≤ m - 1, 0 ≤ j ≤ n = 1, the horizontal duct to the right of (i,j ) has radius and the vertical duct on top of (i,j ) has radius as shown in figure 1b. along the right edge with i = m the nodes have one vertical duct, and along the top edge the nodes have one horizontal duct (except the last).

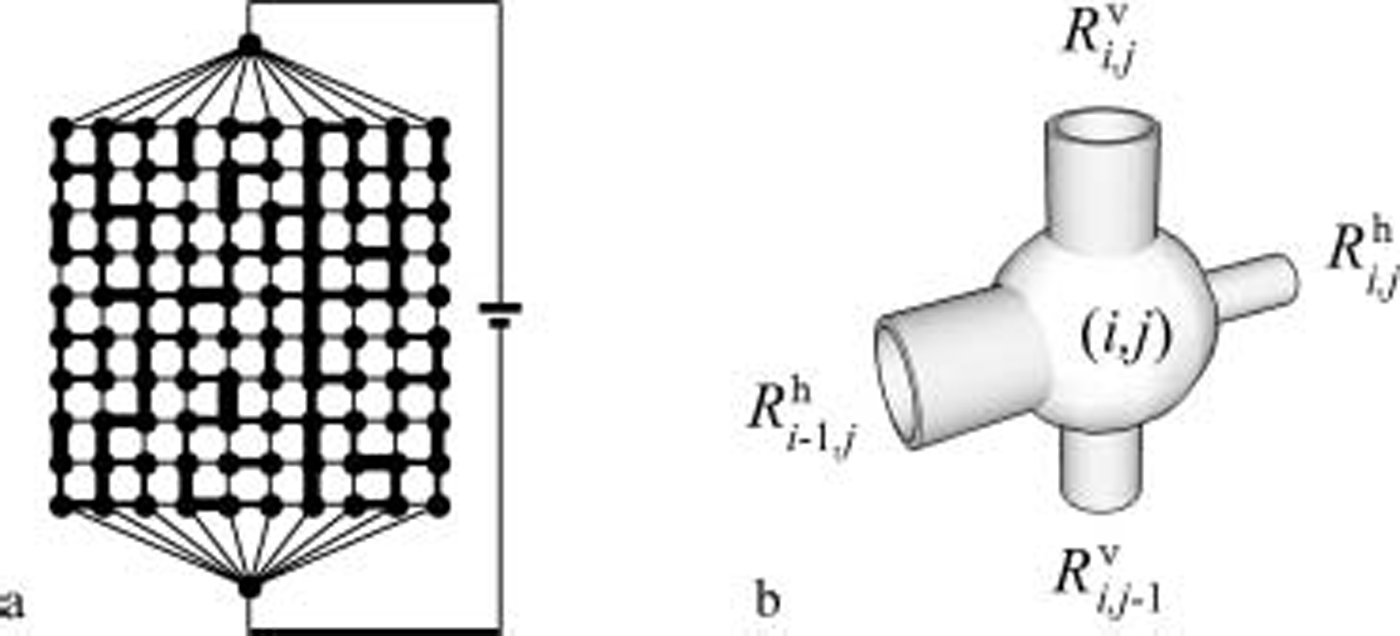
Fig. 1. (a) Random pipe or resistor network. (b) Close-up of a node and adjoining ducts.

For each duct of radius R, the viscous flow within is assumed to have a classic, parabolic poiseuille flow structure, with the maximum velocity at the center of the duct. the flux Q through the duct (Reference DullienDullien, 1992) is given by

(4)

Where ▽P is the constant pressure gradient. this approximation is valid because the flow reynolds number within the brine inclusions is sufficiently small. for each duct connecting two neighboring nodes, the pressure gradient is well approximated by the difference between the pressures at these nodes, divided by the spacing h. given the pressures at neighboring nodes, different fluxes converging to the node (i,j) can be easily computed, and they must balance due to the incompressibility condition. this leads to the following equations,

(5)

For i = 1, . . . ,m - 1, and j = 1, . . . , n - 1, with appropriate modifications on the edges of the lattice. it should be pointed out that this condition is equivalent to the divergence-free condition in a continuous model. at the top of the region (j = n), we assume pi, n = pt, and at the bottom (j = 0) of the region pi _{, 0} = p _b : let Qi _, j be the flux through the vertical duct on top of the (i,j ) node. the total flux through the system is

(6)

Where are the radii of the ducts connected to the top of the sample, and pi _, n-₁ are the pressures at the nodes just below the top surface.

When the sea-ice sample is viewed as a porous medium, the effective permeability k can be defined through

(7)

Where Ū is the average velocity through the medium. we make the connection between Ū and Q̄ through

(8)

Where Lh is the horizontal cross-sectional area of the slice. based on these assumptions, we have the effective permeability

(9)

The microstructure of the slice is described by the duct cross-sectional areas, and we sample them from a log-normal distribution, based on measurements of brine inclusions in first-year sea ice (Reference Thomas and DieckmannPerovich and gow, 1996; Reference Lizotte, Thomas and DieckmannLight and others, 2003; Reference Bock and EickenBock and eicken, 2005). that is, we sample radii R so that log(πR ²) is distributed according to a normal probability density N(μ, σ ²) with mean μ and variance σ ². we also assume that all the random radii are independent from each other. given a particular sample of the duct radii, the volume fraction δ of the slice can be readily computed by

(10)

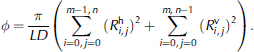
The goal of this study is to investigate the dependence of effective permeability k on the porosity δ, which is reflected in our model by the layout and probability distribution of the duct radii. as an interpolation of measured averages for the cross-sectional area A as a function of brine volume fraction δ (golden and others, 2006), we use

(11)

This function approximates the dependence of the mean cross-sectional area on δ observed by Reference Thomas and DieckmannPerovich and gow (1996) in horizontal thin sections of young, primarily columnar sea ice. in the simulations below, we focus on the permeability in the vertical direction, and ignore observed anisotropy in the medium (Reference FreitagFreitag, 1999; Reference Bock and EickenBock and eicken, 2005). we have investigated making the sizes of the horizontal pipes uniformly smaller, and observed little effect on k, the permeability in the vertical direction. the resulting horizontal permeability decreases correspondingly, though, and observed anisotropy can be modeled in this way, as well as through other related probabilistic approaches currently under investigation.

3. Numerical Results and Discussion

To solve the linear system consisting of equations (5), a large sparse matrix problem is formed, with random entries in the matrix. for large sparse matrices the preferred methods are iterative methods, where an initial guess at the solution is iterated many times with the approximation improved at each iteration, until the resulting approximate solution becomes acceptable. depending on the distribution used to sample the radii, the linear system could be ill-conditioned and therefore difficult to solve, in that the convergence becomes slow. for the work presented here, a multi-grid package is developed and tested for many different distribution parameters μ and σ. in a multi-grid algorithm, the linear system is solved on different levels of grids by a simple iterative scheme. the idea is to take advantage of the fact that low-frequency modes are damped more effectively on a coarse grid. by iterating the approximate solution on different grids via interpolation and restriction, errors of different frequency modes are damped in very efficient ways.

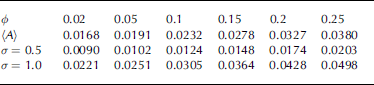
In our simulations, we choose μ and σ to reflect measurements of brine inclusion cross-sectional areas. the procedure is described as follows. the mean cross-sectional area hAi of the inclusions has the volume fraction dependence as shown in equation (11), and we have included this dependence in our simulations. namely, to include the relation hAi = θ(δ) in the model, we use the fact that for a normally distributed random variable X with mean μ and variance σ ²,

(12)

Where E[•] denotes expectation and v[•] denotes variance. in our case, the mean of the areas is specified, and we simulate the log-normal distribution by sampling normally distributed random numbers X with variance σ ² and mean

(13)

The sample value of the area will then be exp(X).

In our first set of simulations we use a dimensionless σ value of 0.5. in our second set of simulations we use a larger value of σ = 1, which roughly corresponds to values of σ measured by Reference Thomas and DieckmannPerovich and gow (1996). a range of standard deviations and mean cross-sectional areas in mm² are displayed in table 1. when the variance in the cross-sectional areas is increased, the coefficients of the resulting linear system become more oscillatory. this poses serious challenges to any solver. on the other hand, the oscillatory structure of the cross-sectional areas is subject to correlations in the distribution, which is assumed to be independent in this model. once the correlation structure is imposed, for example in modeling large channels which span most or all of a sample, the difficulty of dealing with highly oscillatory coefficients should be alleviated to a large extent.

Table 1. Mean and standard deviation of the cross-sectional areas (in mm²) used in the simulations, with corresponding brine volume fractions

Since our model implies

(14)

Then for each value of δ, a particular value is chosen from the above equation to correspond to sea ice with that particular volume fraction. in a multi-grid algorithm, the number of gridpoints has to be a power of 2. in our simulations shown in figure 2 we fix n = m = 1024. by changing the value of L = D, we can match the value of h to the value suggested from the above formula for a specific value of δ.

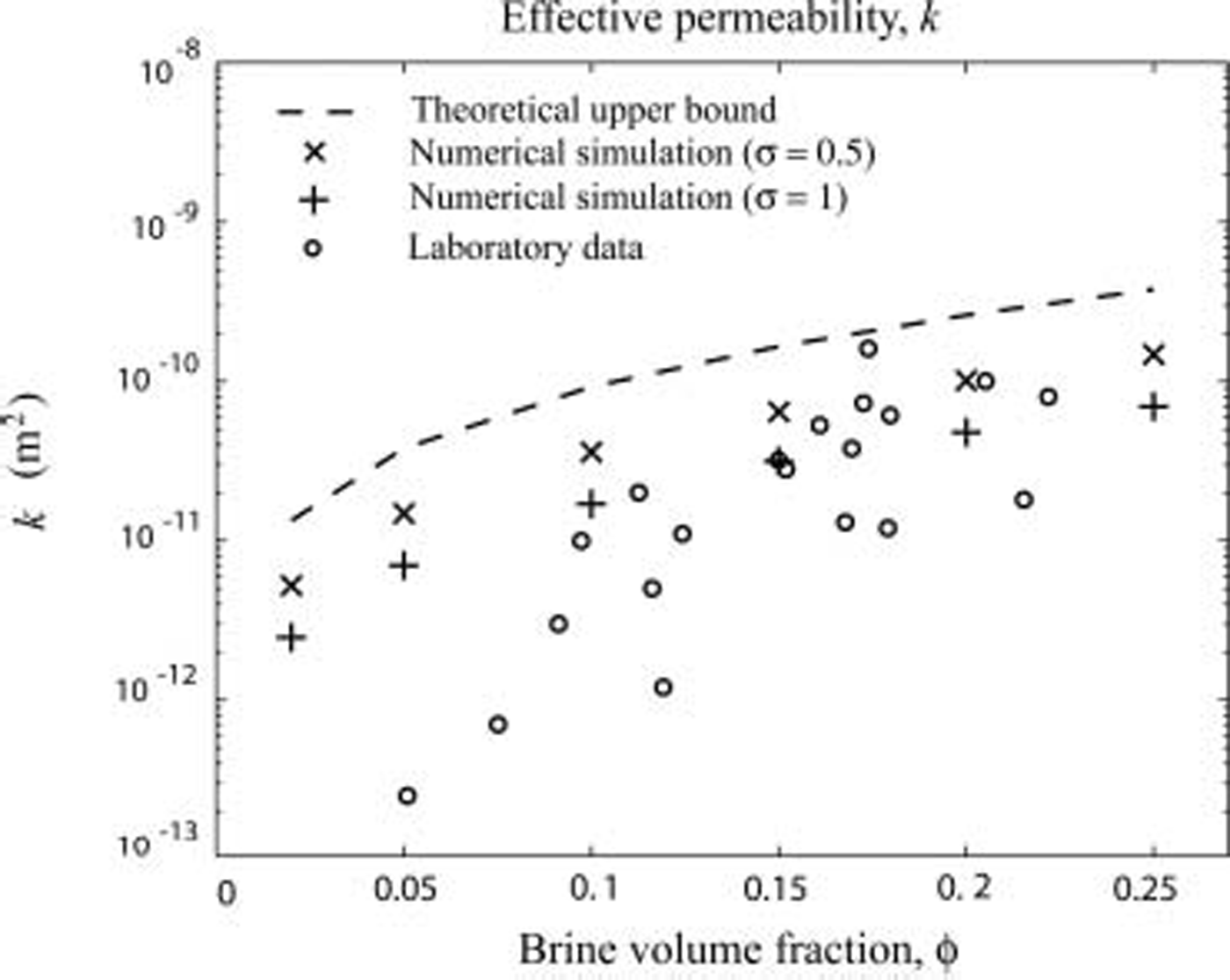
Fig. 2. Comparison of results for the two-dimensional network model with theoretical bounds and laboratory data. Laboratory data are from Reference Friedman and SeatonFreitag (1999) for young, artificially grown sea ice.

Our model of fluid flow through the brine microstructure at this point is two-dimensional and reflects only the most basic features of pore microstructure, with no regard to changes in connectivity with temperature. nevertheless, the results of our numerical simulations shown in figure 2 lie inside void bounds (Reference TrodahlTorquato and pham, 2004; golden and others, 2006) on the permeability of a porous medium. the bounds developed by golden and others (2006) for the vertical permeability of sea ice correspond to pore geometries where all the brine is arranged in vertical pipes each having the same radius R and cross-sectional area A(δ) = πR ² = θ(δ) m² increasing with δ according to equation (11). in this case, the void bound can be written as

(15)

This bound represents the fluid version of the classical arithmetic mean upper bound on the effective conductivity, known since the early 1900s. the general void bounds (Reference TrodahlTorquato and pham, 2004; golden and others, 2006) are optimal within an appropriate class of porous media, and optimal geometries include arrays of vertical pipes. in terms of the above discussion of the values of σ used in the simulations, the bound in equation (15) essentially corresponds to the case σ = 0. in this case, both the network model and the optimal geometry have vertical pipes whose cross-sectional areas are all the same, and increase with σ via equation (11). for the network model, in this special case, the horizontal bonds play no role in bulk vertical transport. as σ is increased from 0 to 0.5 and then to 1 in figure 2, even though some larger-diameter pipes are introduced, net fluid flux through the vertical columns of the network is controlled primarily by the bottlenecks to the flow, or the smallest pipes or constrictions, as in cpa (Reference Fritsen, Lytle, Ackley and SullivanFriedman and seaton, 1998; Reference Golden, Ackley, Lytle, Golden, Heaton, Eicken and LytleGolden and kozlov, 1999). as the variance in pipe radii is increased, more serious bottlenecks are introduced, and the effective permeability decreases, as seen in figure 2. for larger-radius pipes to enhance bulk flow they must be strung together to make larger tubes and channels. however, in the current model there are no such correlations leading to this effect, which will be considered in more detailed microstructural modeling.

For higher values of the porosity, where there appears to be a well-developed connected brine network in actual sea ice, the numerical simulations agree roughly with laboratory data on k in figure 2. measurements were completed with a permeameter on centrifuged ice samples prepared according to Reference Weissenberger, Dieckmann, Gradinger and SpindlerWeissenberger and others (1992), grown artificially in a large-scale tank (Reference Friedman and SeatonFreitag, 1999).

For lower porosities the numerical simulations for both values of σ significantly overestimate observed values for the vertical permeability. in view of the discussion above, the values for the simulation could be lowered in this regime if the network microstructure had even more bottlenecks to the flow, or disconnections of the brine microstructure. of course, one can view an extremely thin pipe connecting two larger fluid regions as a ‘degree of disconnection’. modeling which pays attention to the increasingly disconnected structure of the brine phase as the temperature is lowered appears to be necessary for accurate consideration of the effective fluid transport properties. this finding is entirely consistent with postulated critical behavior of the brine microstructure around a percolation threshold value of δ _c ≈ 0:05 (Reference Golden, Ackley, Lytle, Golden, Heaton, Eicken and LytleGolden and others, 1998). we expect that with generalization of the network model to three dimensions, and with particular attention to disconnection in the brine microstructure as the temperature drops, the numerical results will reflect more closely the behavior of sea ice over a larger range of porosities.