Introduction
The isotopic composition of precipitation is regarded as a powerful tool for investigating palaeoclimate (e.g. Reference JouzelJouzel and others, 1997). The empirical link between the isotopic ratios δ18O and δD of precipitation (hereafter called δ) and local temperature (T) is the basis of reconstructions of climate fluctuations and has been synthesized by Reference DansgaardDansgaard (1964). Although the water isotope ratios are regarded as a valid temperature proxy, there is some debate as to how far this proxy can be used as a climate indicator, because the δ–T relationship appears to vary in space and time (e.g. IAEA, 1992; Reference Cuffey, Alley, Grootes, Bolzan and AnandakrishnanCuffey and others, 1994; Reference Johnsen and GundestrupJohnsen and others, 1995; Reference BoyleBoyle, 1997; Reference JouzelJouzel and others, 1997; Reference Dahl-JensenDahl-Jensen and others, 1999; Reference HoffmannHoffmann and others, 2000; Reference HoldsworthHoldsworth, 2001; Reference Van Lipzig, van Meijgaard and OerlemansVan Lipzig and others, 2002).
To give the isotope thermometer a better physical basis, attempts have been made to model the fractionation process of water in the atmosphere. This has been done using either general circulation models (GCMs) with water isotope tracers, or Lagrangian parcel models based on Rayleigh distillation. The GCM approach is promising, and has reproduced the global variation of δ in precipitation (e.g. Reference Jouzel, Russell, Suozzo and BroeckerJouzel and others, 1987; Reference Hoffmann, Werner and HeimannHoffmann and others, 1998, Reference Hoffmann2000; Reference Mathieu, Pollard, Cole, White, Webb and ThompsonMathieu and others, 2002; Reference Noone and SimmondsNoone and Simmonds, 2002a, Reference Noone and Simmondsb; Reference Werner and HeimannWerner and Heimann, 2002). An advantage of this approach is that it includes all the physical processes involved in determining the δ value: from evaporation at the oceanic source region, mixing of air masses, cloud formation, droplet re-evaporation, to condensation conditions. The impact of seasonality of the snowfall can also be calculated in this way. However, the complexity of GCMs reduces their usefulness for interpretation. Furthermore, the resolution of GCMs is still a limiting factor, especially in describing crucial processes like cloud formation, and precipitation in polar regions. Besides that, the coarse resolution (order of 1–3˚) does not allow a direct comparison with observations of a single snowfall event (Reference HoffmannHoffmann and others, 2000), which hampers full validation.
The other major class of models are Lagrangian parcel models, based on Rayleigh fractionation. These models consider moisture fractionation in an isolated air parcel. They describe condensation and fractionation from a single source area to polar regions assuming immediate removal of precipitation (Reference DansgaardDansgaard, 1964; Reference Jouzel and MerlivatJouzel and Merlivat, 1984). They are useful because they can bypass the need to account for details of the cloud processes (including the microphysics) that influence the fractionation. Thus, they can easily be tuned to accurately quantify the bulk effect of cloud processes on isotopic content. A drawback of Lagrangian parcel models is that due to their descriptive nature they do not realistically describe individual precipitation events, since they do not take into account potentially important factors such as mixing of air masses and evaporative recharge of moisture. However, such simple models are easily modified to test the sensitivity to the inclusion of more complicated physics. Finally, the Lagrangian parcel models are poorly constrained by meteorological data.
In this study, we examine the possibilities of combining meteorological data with an isotope distillation model. The mixed cloud isotopic model (MCIM; Reference Ciais and JouzelCiais and Jouzel, 1994) is used, and three-dimensional, 5 days backward air-parcel trajectories are used as an input for this model. The trajectories are calculated with European Centre for Medium-Range Weather Forecasts (ECMWF; Reading, UK) operational data. The MCIM derives from a Rayleigh distillation model (Reference Merlivat and JouzelMerlivat and Jouzel, 1979; Reference Jouzel and MerlivatJouzel and Merlivat, 1984), and treats processes occurring in idealized air masses, accounting for the mean behaviour of cloud microscale physics. This model has succeeded in generating realistic δ values in East Antarctica (Reference Ciais and JouzelCiais and Jouzel, 1994) and is a valuable tool in studies of source-region characteristics of both present-day snow (Reference Ciais, White, Jouzel and PetitCiais and others, 1995) and precipitation from the last deglaciation in East Antarctica (Reference StenniStenni and others, 2001).
Previously, the MCIM treated the moisture history in a descriptive way. Here, the trajectory approach serves to describe the meteorological history of the moisture more realistically, allowing isotope-modelling results to be compared with an observed snowfall event.
A problem arising when such a model is used for regional studies is the definition of the initial isotopic composition of the vapour. Reference Jouzel and KosterJouzel and Koster (1996) suggested using a GCM-generated isotope distribution as initial conditions. In this study, we calculate initial isotopic ratios of the vapour, necessary to explain the observed δ value of the snow, by an iterative modelling exercise. In this way, the variation in initial isotopic composition of water vapour is explored.
Observations
A large snowfall event in western Dronning Maud Land (DML), Antarctica, in January 2002 has been chosen for this study. This system extended over a large part of DML and is typical for accumulation events in the region (Reference Noone, Turner and MulvaneyNoone and others, 1999; Reference Reijmer and van den BroekeReijmer and Van den Broeke, 2001).
Within the framework of the European Project for Ice Coring in Antarctica (EPICA) the climate of DML is monitored using several automatic weather stations (AWSs). Sensors employed on these AWSs include a sonic height ranger that measures changes in surface height (e.g. Reference Reijmer and OerlemansReijmer and Oerlemans, 2002). In the austral summer of 2001/02, some of the AWSs were visited and snow samples were collected directly under these sonic height rangers. These samples offer the possibility of comparing the timing and related meteorological conditions during accumulation events with associated isotopic composition of the snow. Here we use the results of a snow pit at AWS 6 (74˚28.9′ S, 11˚31.0′ W).
AWS 6 is situated in DML at 1160ma.s.l. at the foot of the steep slope to the high plateau (Heimefrontfjella). The average accumulation of this location is 268 mmw.e. a–1, based on sonic height ranger measurements over the period 1998–2002 and measured snow density. The mean annual temperature is –20˚C, and mean annual surface pressure is 854 hPa (Reference Reijmer and OerlemansReijmer and Oerlemans, 2002). Snow sampling up to 3 m depth was carried out, in order to obtain an isotopic record that is at least as long as the AWS’s record of meteorological data, i.e. 4 years. The sampling increment was 20mm, so an average annual cycle is expected to be represented by ∼32 samples. However, due to unequal timing of precipitation, the thickness of annual cycles is expected to vary. The snow samples are analyzed for isotopic composition at the Centre for Isotope Research, Groningen, The Netherlands. The precision of the mass spectrometer used to determine the isotopic composition of the samples is in the order of 0.1% in δ18O and 2.0% in δD, which results in an accuracy for the deuterium excess (d = δD–8δ18O) of 2.2%. The results are presented in Figure 1.
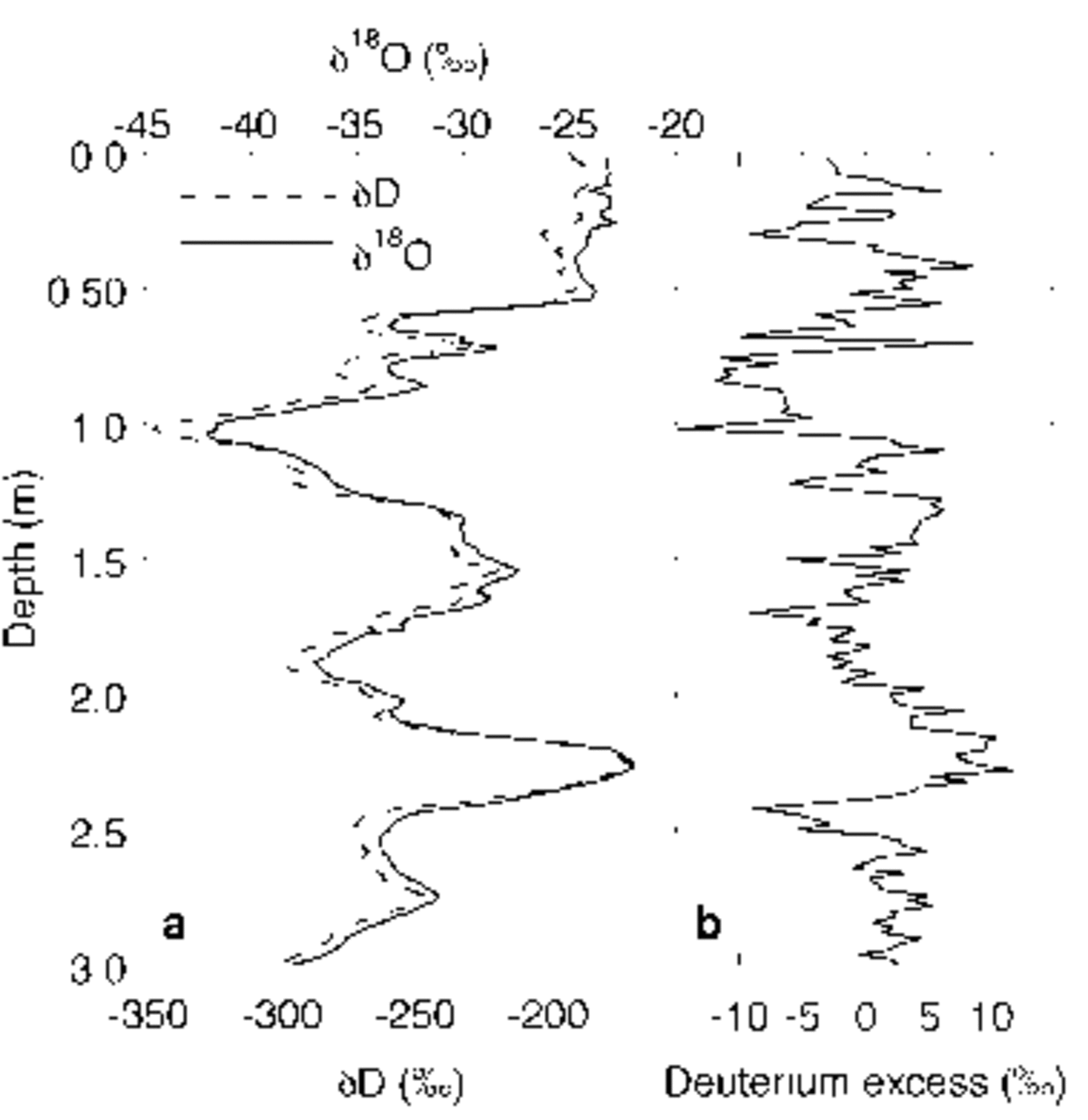
Fig. 1. Isotope profile from snow pit at AWS 6. (a) δ18O (solid line) and δD (dashed line); (b) the deuterium excess signal.
The main measured isotopic variations can be attributed to annual cycles, although not all summer and winter extremes are equally pronounced in the record. This is due to the event-type nature of precipitation and to post-depositional removal of the snow (wind erosion and sublimation), as can be concluded from the 4 year record of the sonic height ranger on the AWS. For this site, approximately ten precipitation events can be identified per year, but only about five per year contribute substantially to the change in surface height (Reference Reijmer and van den BroekeReijmer and Van den Broeke, 2003).
As well as the annual cycles, a top layer of 0.5 m with a fairly constant isotopic composition can be distinguished. The AWS data show that at least the first 0.2 m of this snow layer has accumulated only a few days before sampling, during a major storm event in western DML(Fig. 2). This event lasted from 9 to 13 January and had its maximum on 11 January. Sampling took place on 14 January, so there was insufficient time for diffusion processes to modify the isotopic composition of the snow.
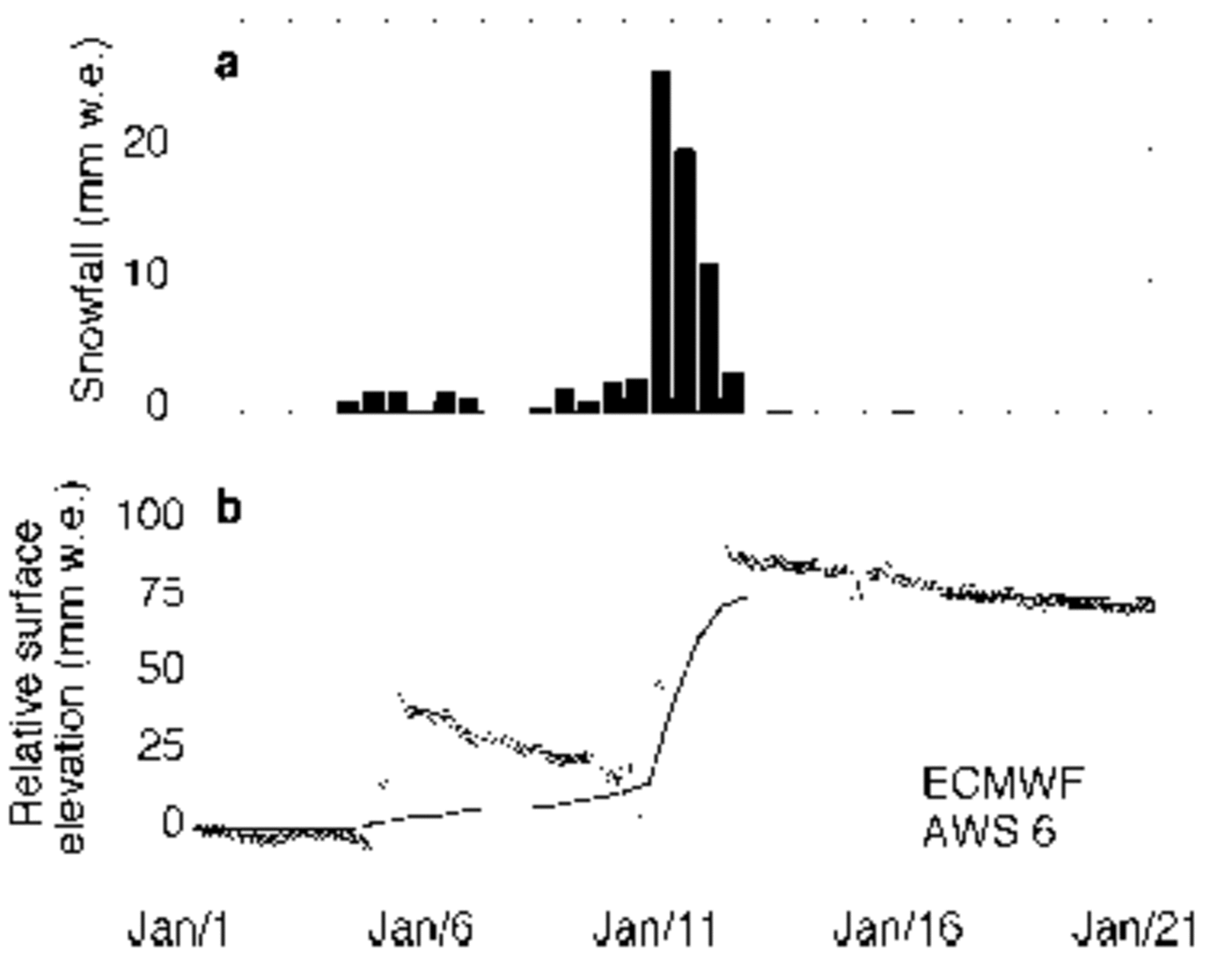
Fig. 2. Measured and modelled snowfall at AWS 6. (a) Snowfall from ECMWF model output; (b) observed (AWS; circles) compared to calculated (ECMWF; solid line) surface height change in mm w.e.
The deuterium excess value, usually used as an indicator for evaporation conditions in the moisture source region, shows an irregular signal in the upper 0.2m (Fig. 1b). It varies between –5% and +6%. On a seasonal scale, however, coherence with the δ18O and δD signals can be observed in Figure 1, with lower excess values in the winter precipitation, and higher values in summer precipitation, ranging from –15% to +11%. The average isotopic composition of the upper 0.2 m of snow from the precipitation event in January 2002 (δ18O=–23.3% and δD=–187.0%) is used in the remainder of this study.
Isotope Modelling Along Trajectories
The model used in this study is the MCIM described by Reference Ciais and JouzelCiais and Jouzel (1994). The MCIM is an extension of earlier Lagrangian models based on Rayleigh distillation, presented by Reference Merlivat and JouzelMerlivat and Jouzel (1979) and Reference Jouzel and KosterJouzel and Merlivat (1984). It describes isotopic processes from its oceanic source region to the precipitation site on the ice sheet, and has succeeded in reproducing the main characteristics of stable-isotope variability in the middle and high latitudes (Reference JouzelJouzel and others, 1997). Depending on the temperature, the MCIM allows for a zone of mixed clouds, where liquid droplets and ice crystals can coexist. During cooling of the air the liquid droplets either evaporate and subsequently condensate to ice, or these supercooled droplets directly freeze onto an ice crystal. This feature is known as the Bergeron–Findeisen process and is associated with kinetic fractionation effects. The importance of these kinetic effects in fractionation is mainly determined by the amount of supersaturation. The isotopic composition of different phases of an isolated air parcel is calculated along a prescribed transport path.
In the original model (Reference Ciais and JouzelCiais and Jouzel, 1994) this transport path was prescribed in terms of temperature and pressure. An important assumption in the MCIM is that the air parcel is transported in (super)saturated conditions, from its source region to the precipitation site, implying continuous fractionation.
Here, the air-parcel history will be derived from a trajectory study. From these trajectories, not only temperature and pressure are obtained, but also information on specific humidity, so that we can estimate whether or not the air is saturated. In this respect it is worth keeping in mind that the humidity of a trajectory parcel is likely to be a small underestimate of the true parcel humidity, since instabilities have been removed in the atmospheric model. This probably introduces a small error into the calculations. Nevertheless, we consider the saturation values from the trajectory study to be representative for the saturation values at the cloud microphysical scale. In case of saturation, we calculate the isotopic fractionation along the trajectories with the MCIM. In case of undersaturation, no condensation is expected, so the water vapour will not change its isotopic composition over this part of the trajectory, provided that there is no evaporative recharge.
Trajectory Model
We used the Royal Netherlands Meteorological Institute trajectory model (TRAJKS) to calculate 5 days air-parcel backward trajectories. This model computes the large-scale three-dimensional displacement of an air parcel. A description of this model can be found in Reference Scheele, Sigmund and van VelthovenScheele and others (1996). The trajectory model has previously been used to calculate backward trajectories to the EPICA drilling site in DML (Reference Reijmer and van den BroekeReijmer and Van den Broeke, 2001) and to several other deep-drilling sites in Antarctica (Reference Reijmer, van den Broeke and ScheeleReijmer and others, 2002).
As input for the trajectory model, the ECMWF operational data are used. This numerical weather-prediction analysis is generally regarded as the best available for the Antarctic region (e.g. Reference Cullather, Bromwich and GrumbineCullather and others, 1997; Reference Connolley and HarangozoConnolley and Harangozo, 2001). The horizontal resolution of this archive is T511 (∼0.36˚), but for the trajectory model the resolution of the input data is kept constant at 1.0° in the horizontal plane, 60 levels in the vertical and 6 hours in time. Interpolation in space and time is therefore necessary. The spatial interpolation is bilinear in the horizontal, and linear in the logarithmic value of the air pressure in the vertical. The time interpolation is quadratic. However, for temperature and specific humidity the quadratic time interpolation produced unrealistic variations over time. For these parameters a linear interpolation is therefore applied, which unfortunately produces less smooth output, but no spurious signals. A test run performed with a spatial resolution of 0.5° resulted in only marginal changes in the trajectory- or isotope-modelling results.
The uncertainty in the calculated trajectories can be considerable. The choice of the type of trajectory, interpolation schemes and spatial resolution of the wind fields introduces an uncertainty in the order of 1000 km after 5 days backward calculation (Reference Stohl, Wotawa, Seibert and Kromp-KolbStohl and others, 1995). In reality, the error can be even larger, due to the presence of convective systems (e.g. fronts, convective storms) or the vicinity of the Earth surface, which can cause the parcel to lose its identity. These errors are difficult to quantify and are excluded from the uncertainty estimate, so computed trajectories must be interpreted with care.
As well as the above-mentioned difficulties, an additional problem of this trajectory approach that can influence the isotope modelling is that not the moisture itself but an air parcel containing moisture is traced. Possible mixing of moisture along the trajectory is not taken into account, since the isotopic content of the ambient water vapour is not known. It should be kept in mind that neglecting this mixing can be a substantial source of error in the results. Nevertheless, we apply the trajectory method because we consider it the best estimate of the transport history. Moreover, it provides the opportunity to compare modelled and observed δ values of precipitation.
Results
The snowfall event of 10–11 January 2002
In January 2002, several precipitation episodes occurred in western DML (Fig. 2). A small accumulation event took place on 6 January, which was followed by a major event on 10–11 January. The average density of this snow as measured on 14 January was 372 kgm–3, which is used to scale the elevation change from the sonic height ranger to mmw.e. (Fig. 2b). Close observation shows a removal of snow in the first few hours of the storm (10 January), lowering the surface below the value of 1 January. This is followed by a sharp increase to a value of around 80 mmw.e.
As a first indication of the capability of the ECMWF model to reproduce the local conditions, the modelled snowfall at the gridpoint closest to AWS 6 is compared to the measured snowfall by the AWS. The horizontal distance between the model gridpoint and AWS 6 is only 2 km, so a comparison with the AWS site seems acceptable. Modelled snowfall is based on the cumulative snowfall in the first 12 forecast hours and suffers from model spin-up. Snowfall from the 0–12 hours forecast is about 9% less than the amount from the 12–24 hours forecast (Reference Turner, Connolley, Leonard, Marshall and VaughanTurner and others, 1999). Due to the orographic nature of Antarctic precipitation, the influence of errors in model orography can be substantial. The location of the study site is near the escarpment region, but the difference between model elevation (1302ma.s.l.) and actual elevation (1160ma.s.l.) is regarded as acceptable.
Figure 2a presents the snowfall as predicted by the ECMWF model at the gridpoint nearest to AWS 6. Over the first half of January, the ECMWF predicts 75.8 mmw.e. (sum of the bars in Fig. 2). Looking at Figure 2, the underestimation of the ECMWF surface height change is only 10%. However, in more detail we can see that the ECMWF model largely misses the snowfall on 6 January, and if we only consider the snowfall during the storm of 10–11 January, the underestimation is 30%. This may seem large, but it is much better than earlier estimates of snowfall by the ECMWF reanalysis data, ERA-15 (1979–93). Reference Reijmer, van den Broeke and ScheeleReijmer and others (2002) show that the ERA-15 dataset underestimates snowfall for Kohnen station in DML by >50%. It should be kept in mind that ECMWF analyses concern grid average precipitation and do not account for inhomogeneous surface conditions.
The peak in snowfall according to ECMWF took place between 10 January, 1200 GMT and 11 January, 0000 GMT. Vertical profiles presented in Figure 3 show a maximum of moisture in the column of air at the gridpoint closest to the sampling site around this date. These vertical profiles are used as an indicator from which pressure levels of the backward trajectories should be calculated in order to find the right transport path of the moisture arriving at the sampling site. In Figure 3, a clear maximum in the profiles of cloud ice water content (CIWC) can be seen. We assume that precipitation formed predominantly at these levels. On 10 January, 1200 GMT, the peak in CIWC was at 675 hPa, while on 11 January, 0000 GMT, this peak can be observed close to 625 hPa.
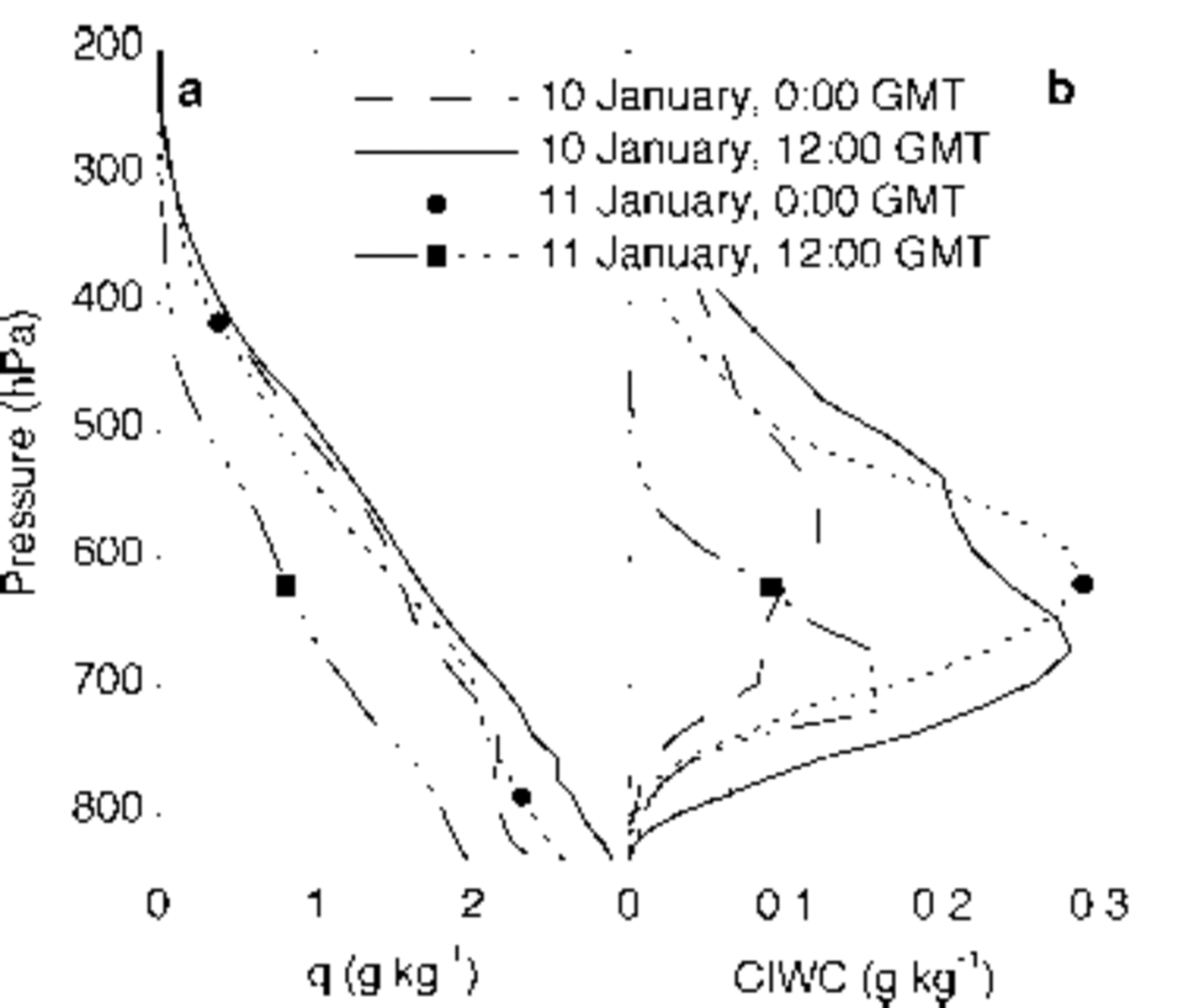
Fig. 3. Vertical profiles above AWS 6 of specific humidity (a) and cloud ice water content (CIWC) (b) at four moments during the storm event.
Trajectories
Six trajectories were calculated 5 days back in time for two arrival times: 10 January, 1200 GMT and 11 January, 0000 GMT, starting at pressure levels ranging from 725 to 600 hPa, with intervals of 25 hPa (Fig. 4). The trajectories with the same arrival time but different starting height do not differ much, but there is a major difference in the trajectories arriving on 10 January, 1200 GMT compared to those arriving on 11 January, 0000 GMT. For 10 January all air parcels were located above the Pacific Ocean 5 days before the precipitation event, whereas for 11 January the air parcels all originated from the South Atlantic. Important to note is the passage of the 10 January trajectories over South America, 3 days before arrival.
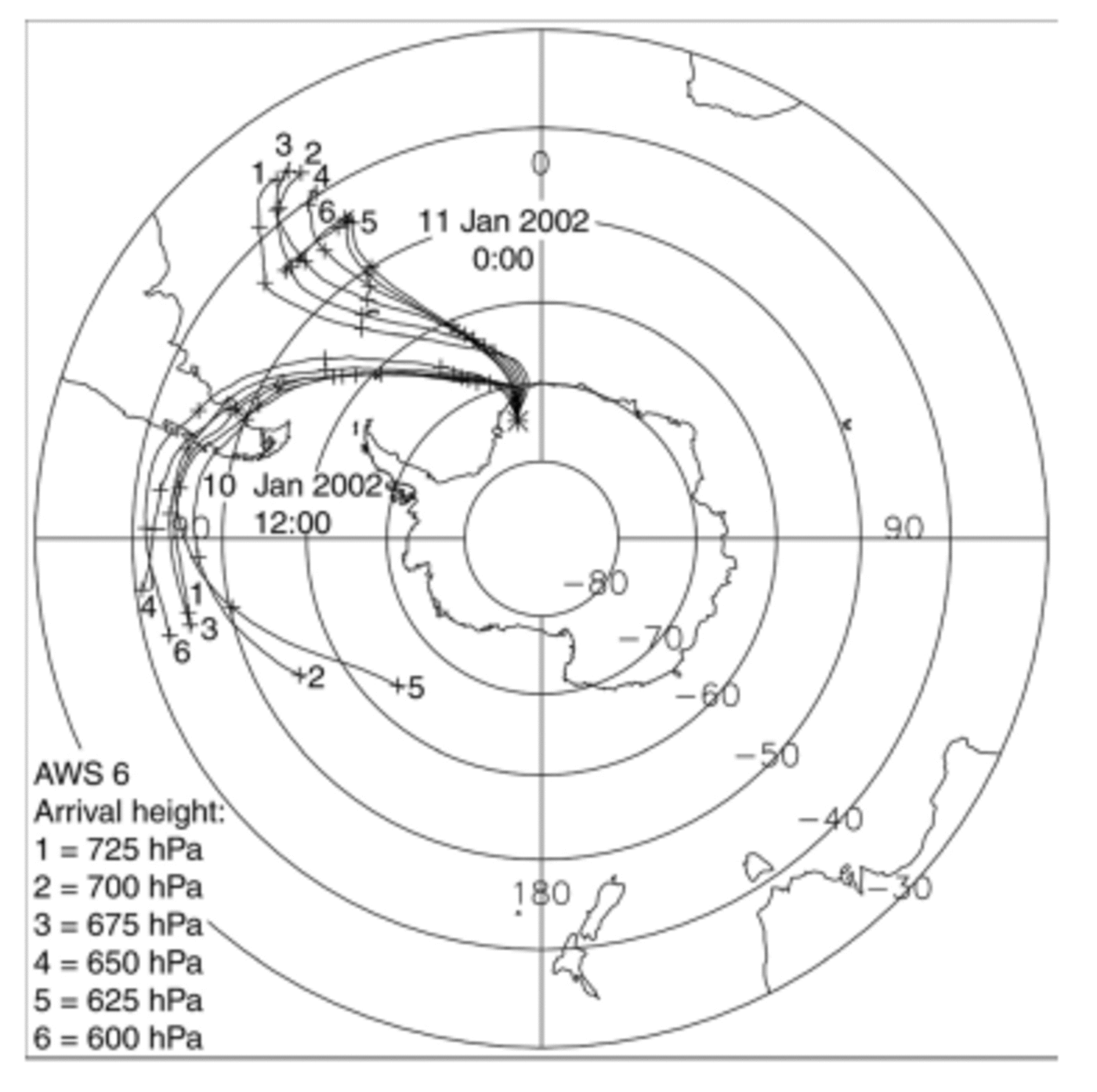
Fig. 4. Five days backward trajectories arriving above AWS 6 at 10 January, 1200 GMT and 11 January, 0000 GMT starting at six different pressure levels above the surface (P 0 = 822 hPa). Each day is marked with a plus sign.
Pressure, temperature, specific and relative humidity along the trajectories arriving at the level of maximum CIWC are plotted in Figure 5. Looking at the trajectory of 10 January (open circles in Fig. 5), the passage over the southern Andes 3 days before arrival forced the air to rise and cool, causing it to lose part of its moisture. After passing South America, this air parcel did not descend sufficiently to pick up any moisture from the South Atlantic Ocean. The specific humidity decreased until AWS 6 is reached. This indicates a moisture source region in the Pacific Ocean. Nevertheless, indications exist that the South Atlantic Ocean is also a source region, since three out of five other trajectories calculated for 10 January (not shown here) show a substantial increase in specific humidity over the South Atlantic Ocean.

Fig. 5. Air-mass properties along the trajectories arriving at the level of maximum CIWC (Fig. 3) for: (a) pressure, (b) temperature, (c) specific humidity and (d) relative humidity.
The trajectory arriving on 11 January (black dots in Fig. 5) shows a small increase in specific humidity from 3 days to 12 hours before arrival. This represents a source region of the moisture in the South Atlantic Ocean between 44° and 67° S. Trajectories from the other pressure levels, which are not shown, indicate a sharper increase of specific humidity north of 50° S or they already contained a large amount of moisture 5 days before arrival.
A remarkable but consistent result is that saturated conditions occurred only hours before arrival at AWS 6, i.e. hardly any fractionation took place previous to that time due to condensation. Only three of the trajectories travelling over South America show saturation over the time while rising over the Andes. These are the only air parcels that could have experienced isotopic depletion before fractionation over Antarctica begins. Otherwise, air parcels travelled southward in under-saturated conditions until they started their ascent onto the ice sheet.
Isotope-modelling results
The modelled isotopic depletion is a function of the difference in water content between the locations of first saturation and the precipitation site. Along most trajectories in this study, condensation does not start north of 67° S. As a consequence, the modelled vapour content at this point has a δ value equal to that of 5 days before arrival, at the starting point of the trajectories. If we assume that the δ value at this point is equal to the value at the moment of evaporation (approximately –10%), then the isotopic depletion due to the rain out between the locations of first saturation and final precipitation is in this case in the order of ∼13% for δ18O, i.e. the water vapour attains a δ18O value of –23%. Upon subsequent condensation, this leads to precipitation with a δ18O value of –11%. Keeping in mind the observed isotopic value of the snow at AWS 6 (δ18O = –23.3%), we conclude that water vapour in the air parcels approaching Antarctica is nothing like sufficiently depleted to explain the observed isotopic composition of the snow. Even when fractionation during the passage over South America is incorporated, the resulting δ values are too high compared with the observed values. In other words, incorporating (under-)saturation conditions along the transport path of the air parcel in the MCIM shows that there is not sufficient condensation for the fractionation to be realized. This result is observed in all identified trajectories, and does not seem to suffer from uncertainties in the trajectory calculations.
Atmospheric mixing along the trajectories with air containing more depleted vapour could lead to a lower δ value at the point where condensation first took place. Another factor that might play a role is that in some cases the water vapour at the starting point of the trajectory has already experienced some fractionation after evaporation from its oceanic source.
To estimate the required δ value of the vapour at the moment of first condensation, an iterative modelling exercise was performed for the 12 trajectories shown in Figure 4. The initial δ18O value of the water vapour needed to achieve snowfall at AWS 6 with a δ18O value of –23.3% was calculated. The fractionation along these trajectories is shown in Figure 6, as a function of specific humidity, both for vapour (dashed lines) and for precipitation (solid lines). The δ18O values for initial vapour range roughly from –24% to –35%. As can be seen from Figure 6, the air parcels arriving on 11 January all show a comparable fractionation over ∼3gkg–1, in contrast to the air parcels arriving on 10 January. The latter have a much shorter range over which fractionation takes place (Fig. 6), owing to the different moment of first saturation along the transport path, which is further south on 10 January.
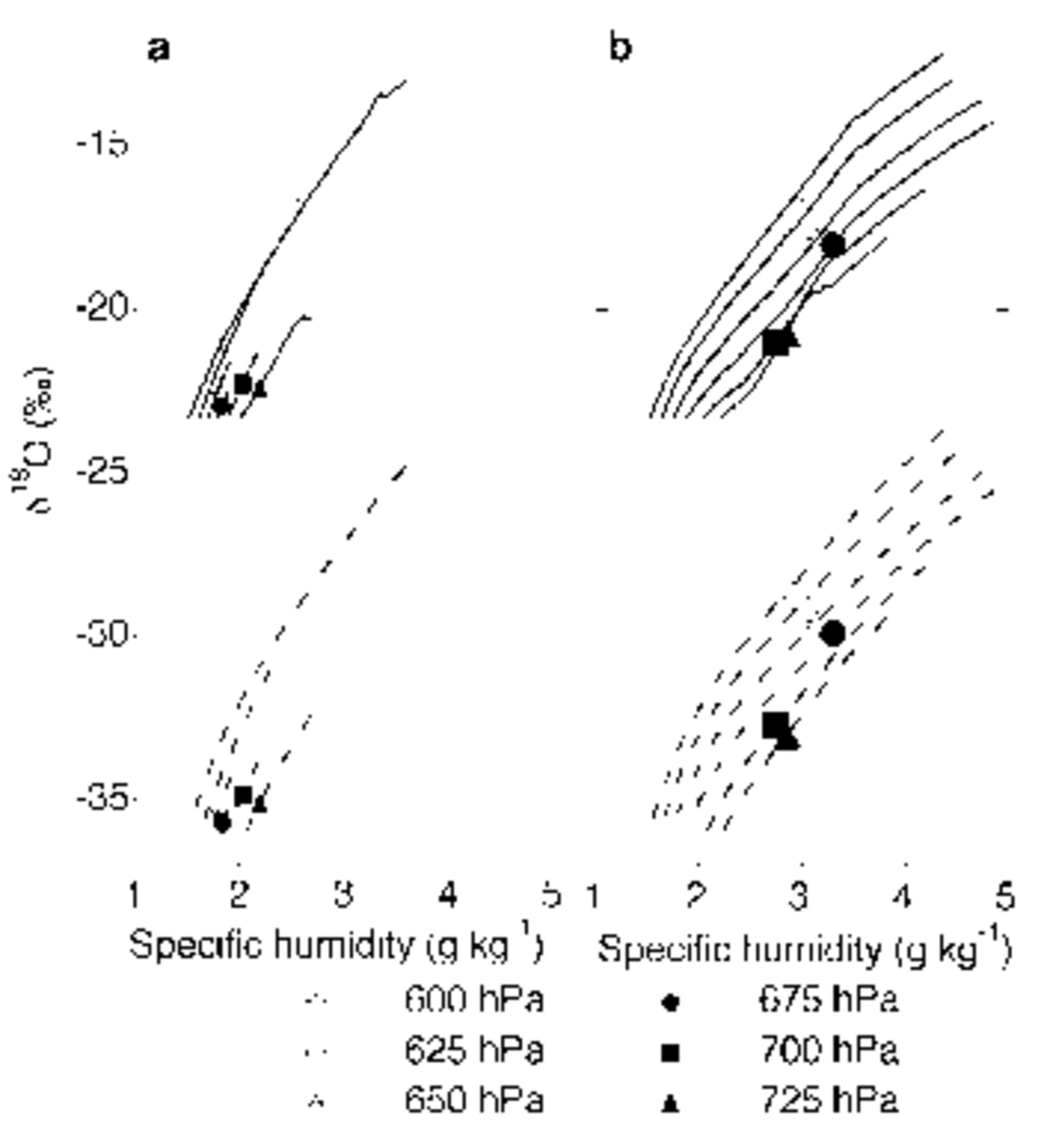
Fig. 6. Oxygen-18 content (δ18O) of the precipitation (solid lines) and vapour (dashed lines) as a function of specific humidity along trajectories. Fractionation along six trajectories arriving at 10 January, 1200 GMT (a) and 11 January, 0000 GMT (b) is plotted. The model has been tuned to the δ value of the precipitation found at AWS 6 (–23.3%). Note the different initial δ values of the vapour as fractionation begins.
The needed initial isotopic composition of vapour seems to be strongly dependent on the spatial position of the air parcel (Fig. 7). With this empirical relation between latitude and δ value as an indication for the initial δ value of the vapour, the MCIM was used again, to recalculate the δ18O value of precipitation at AWS 6. This leads to an average δ18O value of precipitation of –23.0%, in accordance with observed values (weighted with CIWC from Fig. 3).

Fig. 7. Required initial δ18O values of water vapour as function of latitude.
Discussion and Conclusion
Our study shows that, at least for this particular accumulation event, vapour concentration in air is not saturated for the greater part of its transport from the source to the deposition site, according to the ECMWF-based trajectories. Only during the final rise onto the continent does (super)-saturation occur. Continuous saturation is an important assumption in isotope models based on Rayleigh fractionation in order to estimate temperature changes. As our results show, this assumption is not fulfilled along all vapour transport paths. We expect this to be the rule rather than the exception in Antarctica. Only with a spatially dependent isotope field that serves as a starting value for the δ value of the water vapour can Rayleigh-type fractionation models reproduce the observed δ values at the precipitation site.
The question is which processes are responsible for the isotopic depletion of the moisture before fractionation due to condensation occurs. A plausible explanation seems to be atmospheric mixing (by turbulence and convection) during transport to the polar region, and its associated isotopic depletion due to eddy transport (e.g. Reference ErikssonEriksson, 1965; Reference Fisher and AltFisher and Alt, 1985; Reference Kavanaugh and CuffeyKavanaugh and Cuffey, 2003). Besides this, before the trajectories describe the distillation history of the air parcels (i.e. >5 days before arrival), a condensation process could have occurred. This cannot be excluded either, and it can influence the isotopic content of the precipitation as well. The magnitudes of these influences are not known, since these processes are not captured by this trajectory approach.
It is worth comparing this spatial relation of δ values of water vapour with instantaneous isotope fields of water vapour in GCMs, and estimating the natural variability of these isotope gradients in reality. The magnitude of the natural variability of this spatial variation of the isotope field should be studied, for example by vapour sampling for δ measurements on a ship trip to DML. This variability determines the possibility of success of this approach to isotope modelling and of understanding the δ–T relation in time and space.
Acknowledgements
D. Zwartz is thanked for his work in organizing the 2001/02 field season of GPS Observations for Ice Sheet History (GOFISH). Furthermore, we thank the members of the Finnish and Swedish Antarctic Research Programmes (FINNARP and SWEDARP) 2001/02 expedition. We would also like to thank D. van As for all his fruitful comments, and the two anonymous reviewers. The ECMWF provided the meteorological data. This work is a contribution to the ‘European Project for Ice Coring in Antarctica’ (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific programme, funded by the EC and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. This is EPICA publication No. 70. Financial support has been obtained from the Netherlands Organization for Scientific Research (NWO) by a grant of the Netherlands Antarctic Programme.









