Introduction

Temperature distribution in polar ice bodies has long been studied; but there is only scant information about temperature distribution in mountain glaciers of temperate regions because these glaciers were often assumed to be temperate. Recent data compilations (cf. Reference HaeberliHaeberli 1975, Reference Huang, Wong and RenHuang and others 1982, Hooke and others in preparationFootnote *) show that this was a misleading assumption (Reference PatersonPaterson 1981). The occurrence of glaciers which are temperate throughout may, in fact, be restricted to regions with heavy precipitation of > 2 000 mm a⁻¹ (Haeberli in press), and the majority of mountain glaciers in the world may be partially cold. During recent years, there has been increased interest in temperature distribution in Alpine glaciers, in connection with the following fields of study: (a) core drilling projects (e.g. Reference Oeschger, Schotterer, Stauffer, Haeberli and RöthlisbergerOeschger and others 1977, Reference Schotterer, Haeberli, Good, Oeschger and RöthlisbergerSchotterer and others 1981), (b) glacier hazards, such as ice avalanches and glacier floods (Reference RöthlisbergerRöthlisberger 1981, Reference HaeberliHaeberli 1983), (c) the investigation of geomorphological processes, such as the formation of push moraines (Reference Schindler, Röthlisberger and GygerSchindler and others 1978, Reference HaeberliHaeberli 1979), and (d) palaeoclimatic and geothermal studies (Reference Haeberli, Rellstab and HarrisonHaeberli and others 1984).

Modelling temperature distribution in mountain glaciers faces problems not normally encountered when modelling polar ice sheets or ice shelves (cf. Reference PatersonPaterson 1981). These problems mainly concern the high, nonuniform gradients of geometric parameters (inclination, thickness), flow velocities, net mass balance and surface temperatures. Significant changes in these parameters with time also cause problems. Only non-steady-state models may eventually give realistic results.

Problems of numerical stability still make it necessary to use steady-state solutions to test and complete available input data before using models of higher complexity. This paper briefly discusses input data (W H) and first tests (H B) for two examples from the Swiss Alps. The paper is considered to be a preliminary report about continuing efforts to reach a better understanding of temperatures in glaciers (both existing ones or ones which have long since vanished) of the Alps and other mountain regions.

Cases Studied and Data Input

Two examples were selected for first model tests: Grenzgletscher, since it is one of the best documented non-temperate glaciers existing in the Alps today, and Rheingletscher, because it is representative of the large piedmont glaciers of the last ice age in Switzerland.

Grenzgletscher is the main stream of Gornergletscher, one of the largest ice bodies of the Alps. Cold firn from the higher parts of the accumulation area reappears as strikingly white ice (rich in air bubbles) in the glacier tongue, where the temperature of the ice is still below 0° C (Reference HaeberliHaeberli 1975). Figure 1 gives input data for the whole glacier. Information comes from unpublished reports by Süsstrunk (seismic reflection in the ablation area, cf. Reference RöthlisbegerRöthlisberger (1972)), EllistonFootnote * (surface velocity and net mass balance in the ablation area) and Schnyder (unpublished) (net balance at high altitudes). Ice thickness in the accumulation area is estimated using a constant width-to-depth ratio ( 5, cf. Haeberli unpublished); glacier flow at the surface of the firn region where no measurements exist, is estimated by using Glen’s flow law for temperate ice (cf. Reference PatersonPaterson 1981) and smoothed to eliminate irregularities of short wavelength. Surface temperatures are estimated and interpolated from bore-hole studies on other Alpine glaciers, on the Colle Gnifetti (km 14, 4 450 m a.s.l., cf.. Figs. 1 and 2) and on the tongue of the Grenzgletscher (km 5 and 2, 2 600 and 2 500 m a.s.l., cf. Figs.1, 2, and 5). The most recent temperature measurements in bore holes within Grenzgletscher are shown in Figure 2.

Fig. 1 Grenzgletscher: input data for model calculations; d is glacier thickness, v is surface velocity, b is net mass balance, T is 10 m temperature. The front of the glacier is at km 0. High value of basal shear stress τ indicates high glacier activity in a region with abundant precipitation.

Fig. 2 Grenzgletscher: bore-hole temperatures. Level of temperature scale indicates depth (−y) of glacier bed below surface. Bore hole 1: Colle Gnifetti (km 14, y = 0 at 4 450 m a.s.1., measured in 1978). Bore hole 2: glacier tongue (km 5, y = 0 at 2 600 m a.s.l., measured in 1979). Bore hole 3: glacier tongue (km 2, y = 0 at 2 500 m a.s.l., measured in 1980). Indicated temperatures were taken after thermal stabilisation of either the air-filled (bore hole 1) or the water-filled, refrozen bore hole (bore holes 2 and 3). Curve a for bore hole 3 is calculated (cf. Fig.5).

Fig. 5 Grenzgletscher: calculated temperature distribution in the region of bore holes 2 and 3 (cf. Figure 2 for bore-hole information and vertical scale and Figure 1 for surface input data). Boundary condition is δT/δx = 0 at km 1 and phase equilibrium temperature at the glacier bed (cf. Reference HarrisonHarrison 1975). The calculated temperature profile at bore hole 3 is illustrated in Figure 2.

Rheingletscher was one of the large piedmont glaciers of the Alps in existence during the last ice age. The geometry of this ice body was reconstructed on the basis of geological evidence by Reference JäckliJäckli (1970) and, more recently, by Reference Keller and KrayssKeller and Krayss (1980). Input parameters are given in Figure 3. Flow velocities again are calculated with the use of Glen’s flow law for temperate ice to obtain upper limits. Balance values are estimated from ice discharge and continuity considerations, and are adjusted to give the balance gradient a more or less constant value (for simplicity). Surface temperatures are based on geocryological reconstructions of periglacial palaeo-temperatures, on air-temperature gradients of 0.65°C 100 m⁻¹ (very questionable assumption) and on empirical relationships between air and ice (firn) temperatures (Reference HaeberliHaeberli 1982). However, all numbers are uncertain, and in some cases (balance gradient, velocity), their accuracy is limited to orders of magnitude only. But it is worth noting that all values indicate clearly that the piedmont glaciers of the last ice age existed under cold and dry climatic conditions (low precipitation → low temperature at the equilibrium line → low mass-balance gradient → low mass flux → low shear stress and low velocity, cf. Haeberll (in press)).

Fig. 3 Rheingletscher, 18 ka BP: input data for model calculations. Explanation cf. Figure 1, v’ is smoothed velocity profile used for test run (cf. Fig.6). Low value of basal shear stress indicates low glacier activity under continental climatic conditions.

Model Calculation: Two-Dimensional Steady-State Solution

The differential equation for the two-dimensional distribution of the temperature T(x,y) in a moving medium with constant thermal diffusivity k and a constant geometry with constant boundary conditions is

is the velocity vector as a function of the location P(x,y):

The geometry used for the calculation 1s illustrated in Figure 4. The surface of the glacier is taken as

Fig. 4 Coordinate system and geometry of the glacier as used for calculations, v is the velocity vector at the point P(x,y) and d is the glacier thickness at x.

horizontal for y = y₀ and the glacier bed then follows a line

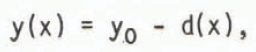
with d(x) as the thickness at the position x.

The following assumptions for the velocity field have been made for the calculations: (a). The horizontal velocity component v_s(x) = v_x(x,y₀) for the glacier surface and the horizontal velocity component v_b(x) = v_x(x,y₀-d(x)) at the glacier bed (sliding velocity) are either estimated or calculated as explained in the previous section (Fig.1). (b). The horizontal velocity component v_x(x,y) as a function of the depth below the surface is calculated using a 4th power law corresponding to Glen’s law for a uniform channel with constant flow-law parameter A and a flow law exponent n = 3:

where y₀−d(x) < y < y₀. (c). The vertical component v_y(x,y₀) of the velocity vector at the glacier surface is taken as the negative net mass balance −b as illustrated in Figures 1 and 3.

(d). The vertical velocity component V_y(x,y) as a function of the depth below the surface is taken to be linear:

again for y₀−d(x) < y < y₀.

For the chosen geometry, the bed of the glacier is not parallel to the x-axis and therefore, the vector components described above do not correspond exactly to the “horizontal” and “vertical” components in reality. This effect is more severe closer to the bed. On the other hand, the velocity decreases closer to the bed and the slope angles are small except for the glacier terminus, and therefore, the error made remains small.

The ELLPACK program (Reference RiceRice 1980) (available at the ETH-Zürich’s program library) was employed for solving two-dimensional elliptic differential equations for steady-state conditions. This program allows the input of a given geometry by defining the margin with curved parts and a boundary condition for each curved part and a given velocity field. As boundary conditions, a° temperature function, a temperature gradient or a mixed condition can be used.

With respect to the often-used “moving column” model (Reference Radok, Jenssen and BuddRadok and others 1970, cf. Reference HookeHooke 1977, Reference SugdenSugden 1977), the model presented here allows for true two dimensional solutions and can take into account realistic velocity distributions. The result of the computations is replotted for the actual geometry of the glacier.

Figures 5 and 6 show examples of test runs. In the case of Grenzgletscher (Fig.5), the temperature information from bore hole 2 (Fig.2) was used as a boundary condition at km 5 to simulate the temperature distribution in a down-glacier section measuring 4 km in length; bore hole 3 is also sited within this distance, at km 2. In addition to the surface data (cf. Fig.1), a constant temperature at the glacier bed (approximately corresponding to the phase equilibrium temperature) and a zero gradient δT/δx = 0 at the vertical end at km 1 were chosen as boundary conditions. As a result, the calculated temperature distribution corresponds in a qualitative way to the temperature profile observed in bore hole 3 (Fig.6). However, the model gives somewhat higher temperatures and does not simulate the observed irregularities of the temperature profile in detail. Deviations of the observed profile with respect to the calculated profile are thought to be due to historical changes in glacier geometry, ice flow and surface boundary conditions. More complete temperature measurements and non-steady-state calculations are therefore necessary to reach better agreement between observation and calculation. Despite these uncertainties, the calculation illustrates the fact that cold glacier ice can be easily transported over long distances by the movement of the ice in Alpine glaciers, even within zones of temperate surface temperatures. No model calculation has been done so far for the entire glacier. The results of the test run between bore holes 2 and 3 and the high velocity of the ice in the accumulation area as indicated in Figure 1, however, make it easy to assume that advection of cold ice from the high altitude part of the accumulation area is indeed the cause of the temperature distribution in bore hole 2 (Fig.2) and in the glacier tongue.

Fig. 6 Rheingletscher, 18 ka BP: calculated temperature distribution. Broken lines indicate regions of numerical instability in the calculation.

The example of Rheingletscher (Fig.7), the iceage glacier of 18 ka BP, again shows the strong effect of ice advection on the englacial temperature distribution. In addition to surface data (cf. Fig.3), δT/δy at the glacier bed was chosen as 0.015°C m⁻¹ about half the value actually observed in the Swiss plateau). The choice of this important boundary condition illustrates perfectly the uncertainty of steady state calculations. Both the temperature of the glacier bed and the temperature gradient vary with changes in all other parameters. Also, the calculated temperature gradient at the glacier bed, again makes the choice of boundary conditions difficult. In fact, it is possible to construct almost every desired englacial temperature distribution by varying this input parameter. The chosen value represents a rough compromise; near the glacier front, where relatively warm glacier ice may have overridden relatively cold (perennially frozen) ground, heat flow may have been extremely weak, zero or even negative (into the earth), and 0.015°C m⁻¹ may be too large a temperature gradient. However, 30 to 50 km behind the front, where very cold ice must have overridden relatively warm (thawed) ground, much higher temperature gradients probably occurred. Thus, the boundary condition at the glacier bed should be varied as a function of x, but this will only be possible on the basis of improved knowledge about temperature variations and glacier fluctuations as functions of time. The example of Rheingletscher also illustrates the problem of numerical instability. The velocity profile calculated from the reconstructed glacier geometry had to be smoothed by a factor of about 5 (v’ in Fig.3), to allow for more or less stable solutions. Even then, however, the lower part of the glacier (the “ablation area”) remained highly unstable. Thus, this model is probably more useful for testing the sensitivity of the temperature field to various parameters (e.g. variations in boundary conditions, variation of the velocity field of the ice movement and variations of the thermal properties, like thermal diffusivity as a function of the location or of the temperature itself) rather than for simulating accurately the temperature distribution in existing or former glaciers. Nevertheless, the calculation of the temperatures for Rheingletscher indicates that the glacier bed may have been temperate only in a relatively narrow zone near the glacier front, and that very cold ice was brought down to low altitudes by ice movement. This latter effect may have greatly enhanced the depression of temperatures during 18 ka BP at the Earth’s surface in certain regions. For example, in the region of Sargans at km 120, ground surface temperatures may have been colder than in periglacial regions with the same altitude by about 10°C, thus greatly enhancing geothermal effects in the Earth’s crust (cf. Reference Haeberli, Rellstab and HarrisonHaeberli and others 1984).

Conclusions and Outlook: Non-Steady-State Solutions

Theresults of modelling the temperature distribution in Grenz-and Rheingletscher clearly point to the importance of ice advection in non-temperate mountain glaciers. However, they also show that accurate modelling of such glaciers is only possible if the combined history of boundary conditions and glacier fluctuations can be considered in non-steady-state type calculations. Another program, using finite elements, is being prepared. It solves the same differential equation, in this case for time-dependent boundary conditions, but still for a non-variable geometry. Only such non-steady-state calculations may eventually give more realistic results. At the present level of knowledge steady-state solutions may help to improve the incomplete data basis as well as our understanding of the complicated and interdependent processes involved.