1. Introduction: The Main Physical Processes in Powder-Snow Avalanches

Powder-snow avalanches (PSAs) tend to assume a mythical aura in people’s minds due to their often enormous size, high speed and resulting large devastated areas. On the practical side, true PSAs are a relatively rare phenomenon and only a modest fraction of avalanche damage is caused by them. Nevertheless, avalanche-hazard mapping in mountainous areas needs to take into account PSA effects. In view of the demand for reliable estimates of PSA trajectories and pressures, several models of different degrees of sophistication have been developed over the past few years (Reference Fukushima and ParkerFukushima and Parker, 1990; Reference Brandstätter, Hagen, Sampl and SchaffhauserBrandstätter and others, 1992; Reference Hermann, Issler, Keller, Wagner, Hirschel, Périaux and PivaHermann and others, 1994, Reference Hermann, Issler, Keller, Buisson and Brugnot1995; Reference Rapin and BrugnotRapin, 1995; Reference NaaimNaaim, 1995). Many of them draw heavily on earlier work that has already been reviewed by Reference Scheiwiller and HutterScheiwiller and Hutter (1982) and Reference Issler, Gauer, Schaer and KellerHutter (1995).

Two shortcomings appear to be shared by all the PSA models in use today: (i) the formation of the PSA from a dense-flow avalanche (DFA) and their subsequent interaction are not modelled; (ii) snow entrainment and deposition—two decisive effects — are completely neglected or incorporated through ad hoc assumptions. In order to address the second point and open the door to dealing with the first, we adopt the picture of PSA structure and formation proposed by Reference NoremNorem (1995) on the basis of observations (Reference Schaerer and SalwaySchaerer and Salway, 1980; Reference Norem, Kvisterøy and EvensenNorem and others, 1985; Reference Nishimura, Maeno, Kawada and IzumiNishimura and others, 1993; Reference Issler, Gauer, Schaer and KellerIssler and others, 1996), the similarity with snowdrift and a qualitative analysis of shear stresses. A physical description of snow entrainment and deposition is obtained and rough estimates of the model parameters can be given. Straightforward modifications to be described elsewhere will allow coupling to a DFA model.

The main assumptions in the present model are the following:

• 1. The PSA can approximately be described in terms of a so-called saltation layer with a density in the range 20–50 kg m⁻³ and a suspension layer (the powder-snow “cloud”) of lower density (1–10 kg m ⁻³).

• 2. Snow particles in the saltation layer eject other particles when they hit the snow cover (or DFA surface). This is assumed to be the dominant factor for the mass balance and ground friction of the PSA. The yield number of ejected particles per landing particle) is taken to be a slowly varying function of the impact energy.

• 3. The depth of the saltation layer is determined by the average slope-perpendicular velocity imparted to ejected particles, which is assumed to be a fixed fraction of the average landing velocity.

• 4. Mass exchange between the saltation and suspension layers is due to the turbulence at the bottom of the suspension layer and settling of particles under gravity.

• 5. Momentum exchange between the saltation and suspension layers is due to drag on the saltating particles as well as to mass exchange.

2. The Suspension Layer

In the following, the subscripts f and p stand for the fluid (air) and the particles (snow), respectively. Their effective densities, ρ_f,p , and the mixture density, ρ, are expressed in terms of the intrinsic densities, , and the volumetric particle concentration c. Setting , one finds

(1)

The mixture velocity is defined in terms of the fluid and particle velocities and densities by . The Stokes number — the ratio of the particle relaxation time and the typical flow time-scale, St ≡ t_p/t_f — is relatively low at 0.1 – 1. Therefore, we approximate the relative velocity between phases, u ≡ U_p — U_f, by the average settling velocity of the particles, .

Given the high Reynolds numbers of PSAs, some form of turbulence modelling is required. To this end, fields are split into mean and fluctuation components. . For the mixture velocity, Favre-averaging is used: with .

The equations generally contain terms with correlations of two or more fluctuation fields. Invoking the eddy-viscosity and eddy-diffusivity concepts, we set

(2)

in approximations (2), higher-order correlations that are expected to be small have been neglected. The Prandtl numbers σ_c etc. characterize the transport properties of the respective quantities c, … under turbulent velocity fluctuations. The turbulent viscosity is modelled as

(3)

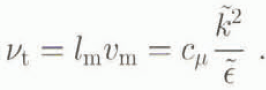
Prandtl’S mixing length and mixing velocity, and are expressed in terms of the (Favre-averaged) turbulent kinetic energy, , where

(4)

and the turbulent-dissipation rate, is an empirical constant.

Henceforth, suppressing overlines and tildes, the balance equations for air and particle mass can be expressed as the mixture mass balance and the transport equation for the concentration field,

(5)

(6)

The righthand side of Equation (6) describes settling and turbulent diffusion of particles with respect to the barycentric velocity field. Due to variable particle concentration, the latter is not divergence-free even though we consider the air as incompressible. Combining Equations (5), (6) and (1), we obtain

(7)

Adding the momentum balances of the two components leads to

(8)

with g the vector of gravitational acceleration. The mixture pressure is defined as p = P_f + P_p − p_atm. with the ambient pressure P_atm. subtracted, and the mixture deviatoric stress as . The viscous part of the stresses appearing in Equation (8) is modelled in terms of the mixture viscosity υ like the term involving the settling velocity ω _s, it is usually negligible compared to the turbulent-shear stresses. The next-to-last term in Equation (8) is a consequence of using Favre-averaging for U; the last term predicts turbulent-shear stresses due to density gradients even without velocity gradients.

Equations (5)–(8) have to be complemented by a set of equations determining k and ∈ so that υ can be calculated. We chose the k−∈ model (Reference Launder and SpaldingLaunder and Spalding, 1974) as a compromise between accuracy on the one hand and reliability and speed on the other. It consists of transport equations for k and ∈,

(9)

(10)

(A slightly simplified version of the buoyancy term for ∈ is used here in view of ambiguities in its formulation.) From a long series of validations, the following set of values is recommended for the model coefficients (Reference Launder and SpaldingLaunder and Spalding, 1974):

(11)

The boundary conditions at the upper and lateral surfaces of the computational domain depend on model implementation as a free-surface flow or as a boundary-layer flow and will be discussed in section 4. Those on the bottom surface, describing mass and momentum exchange with the saltation layer, will be developed in section 3.

3. The Saltation Layer and its Boundary Conditions

The currently limited experimental knowledge of the saltation layer, its shallow depth and the hopping motion of particles suggest a somewhat simplified treatment that neglects the air mass balance and uses depth-averaging to avoid explicit calculation of the velocity and density profiles. Figure 1 illustrates our notation and the mass fluxes. Based on experience from sand and snowdrift investigations (Reference BagnoldBagnold, 1941; Reference KikuchiKikuchi, 1981; Reference Pomeroy and GrayPomeroy and Gray, 1990), the depth of the saltation layer, h₂, is taken to be proportional to the square of the average saltation velocity U ₂,

(12)

g’ is the component of gravity perpendicular to the surface; g’= gcosϕ an inclined plane but also centrifugal forces due to curvature can be taken into account. From measurements in the held and in wind tunnels, .

Fig. 1. Schematic view of the structure of a powder-snow avalanche according to Reference NoremNorem (1995). Some quantities relevant to the model described in the text are also indicated. Subscripts 1, 2 and 3 on field validities generally refer to the snow cover, saltation layer and suspension layer, respectively.

Neglecting the air, the snow mass balance of the saltation layer is written in terms of the depth-averaged density and velocity as

(13)

(The subscript on a vector indicates that only the components parallel to the surface are considered.) Apart from advection. the mass can change due to snow entrainment from the ground at a rate Q_erod, snow deposition (Q_sed), transition of particles from saltation to suspension (Q_susp), and settling from the suspension layer to the saltation layer (Q_sett). Similarly, we write the depth-averaged momentum balance as

(14)

S_ρ UU ≈ 1 and are form factors that arise when the depth-averaged product of fields is expressed as the product of the depth-averaged fields. A more precise determination would require knowledge of the vertical profiles of ρ and U. is the unit vector normal to the surface.

The average velocity at which particles hit the ground is modelled as with is the corresponding factor for particles entering the suspension layer. (β₂Q_erod )/(β₂Q_sed ) with β < 1 is a measure for the fraction of momentum transmitted from impinging particles to ejected particles; β₁ = 0 if only aerodynamic entrainment were to take place. Small adjustments would be needed to describe momentum exchange with a dense-flow avalanche. In a fully three-dimensional treatment, is the mixture velocity at the bottom of the suspension layer and γ_i = 1; in a shallow-water-type approach, γ₁ ≳ 1 is the ratio of the velocity at the bottom of the suspension layer and the depth-averaged suspension velocity, U₃.

The particle-settling rate from the suspension layer to the saltation layer is proportional to the settling velocity and the particle concentration at the bottom of the suspension layer:

(15)

where c(z₂ ⁺) is either obtained from a three-dimensional calculation of the suspension layer or is expressed as in terms of the depth-averaged suspension concentration: the proportionality constant from laboratory measurements (Reference KellerKeller, 1995) and three-dimensional numerical simulations.

Assuming that the idealized interface between layers is narrower than the size of the dominant eddies contributing to turbulence, the turbulent Upward flux through the interface is given by the product of particle concentration just below the interface, with β₄ ≲ 1, and the average upward velocity, , and analogously for the turbulent downward flux (Fig. 2). Up to settling effects, and

(16)

The suspension rate is therefore expressed as

(17)

Deviations from isotropic turbulence can be accounted for by changing the coefficient of k in approximation (16). In a shallow-water-type approach one sets c(z₂ ⁺) = γ₂C₃ and K(z₂) = γ₃K₃ in terms of the layer-averaged values; from three-dimensional simulations and density-weighted depth-averaging. The particle-sedimentation rate. Q_sed , is equal to the landing rate of particles, i.e. the saltating mass above unit area divided by the average saltation time. Expressing the latter in terms U₂ , we obtain

(18)

Our model for Q_erod is guided by the snowdrift analogy: saltation is maintained mostly through particle ejection at impacts. The initial kinetic energy of ejected particles and hence the depth of the saltation layer grows with the average velocity in the saltation layer. The number of ejected particles must then be a slowly varying function of U₂ ² ; at saltation threshold, on average one particle is ejected per landing particle. Currently, lacking an impact model, we set

(19)

From observations of snowdrift, , depending on snow conditions. The estimation of α is more critical, because of the exponential growth of particle density in such a “chain reaction”. We make use of the observation that a significant saltation layer is usually formed after the DFA has travelled 300–500 m on a track without cliffs. At a typical relative velocity between air and avalanche surface of 30 m s⁻¹, saltation heights are around lm, saltation durations are around 1 second and saltation distances are of the order 20–30m. Starting from the density of snowdrift (c ≈ 10⁻⁵), the particle number increases by a factor of 10³−10⁴ in 10–25 jumps. We therefore obtain the rough estimate α ≈ 0.01–0.1.

Fig. 2. Schematic diagram of the principal mechanism for particle suspension: turbulent eddies exchange a dense mixture from the saltation layer (particle concentration c(z₂ ⁻) with a lower-density mixture from the suspension layer (c(z₂ ⁺)). The average exchange velocity is .

Reference OwenOwen (1964) described a self-regulating saltation mechanism that maintains the aerodynamic shear stress on the bed at the minimum value for bed mobility: . where is the wall-shear velocity below which saltation ceases; this term is therefore negligible except in the very early and very late phases of a PSA. is the aerodynamic shear stress exerted by the suspension layer, as discussed in section 2. The saltating snow acts as an efifective surface roughness r that grows with the saltation height and density. A first-principles determination of r would require precise calculation of saltation trajectories and their effect on the wind field in the saltation layer. In order to obtain an approximation, we assume that: (i) the velocity profile just above the saltation layer is logarithmic, (ii) τ_f,2 is mainly responsible for accelerating the ejected particles from β₁U₂ to β₂U₂ and (iii) Q_erod ≈ Q_sed . Equating the aerodynamic shear stress to the momentum gain of the particles leads to

(20)

Inserting Equation (18) and solving for r, we have

(21)

where k ≈ 0.4 is the von Kármán constant. Finally, we obtain

(22)

Using the estimated value ranges of β₀, …, β₃ , an effective ground-friction coefficient of is obtained.

It is noted that the parameters of the model have a clear physical significance. It appears feasible to obtain better estimates for them by an iterative procedure: Saltation trajectories are computed for an assumed air-velocity profile in the saltation layer and then the effect of the particles on the air velocity is accounted for, and so on (Reference Anderson and HaffAnderson and Haff, 1988). The erosion rate stands apart, because a better model of the impact process is needed for a significant improvement.

4. Implementations and Applications

Numerical implementation of the model described in the previous sections is currently in progress. For fully three-dimensional simulations, Reference Hermann, Issler, Keller, Wagner, Hirschel, Périaux and PivaHermann and others (1994) and Gauer have implemented the suspension-layer model on the basis of a commercial flow solver (CFDS-CFX 4.1; a body-fitted structured grid, finite-volume code with among other choices — the k−∊ turbulence model) and supplemented it with a simple erosion model (Reference Fukushima and ParkerGauer, 1994) that calculates the erosion rate as a function of the turbulent kinetic energy near the ground: the erosion mass flux is given by

(23)

with

(24)

and the dimensionlcss shear velocity Z defined by

(25)

u_* and d_p are the shear velocity at the snow-cover surface and the average particle diameter, respectively.

The computational grid has to be chosen sufficiently large, so that recirculation of the displaced air is not hindered; no-slip conditions can then be imposed on the top and lateral boundary faces. Air entrainment at the upper PSA surface takes place within the computational domain and is computed by the model. At the bottom surface, the mass flux is prescribed by the entrainment model and the (aerodynamic) wall-shear stress is computed from the turbulence in the flow by means of wall functions (Reference Launder and SpaldingLaunder and Spalding, 1974) and the prescribed roughness height.

A recent PSA event at Albristhorn in the Bernese Oberland (Reference Issler, Gauer, Schaer and KellerIssler and others, 1996) enabled a first test of the implementation with the simple erosion modelFootnote *, because the initial conditions are reasonably well known and the extent of damage to the forest and buildings had been mapped together with the deposition zones of the dense-flow and powder-snow parts. Simulation without erosion and deposition failed, giving very high velocities in the early phases and too-low pressures in the run-out zone. When deposition and the simple erosion model with standard parameter values (Reference Fukushima and ParkerGauer, 1994) (average particle-settling velocity ω_s = 0.5 ms⁻¹, erosion coefficient E_s = 5.2 × l0⁻⁵, erosion threshold Z_c = 3.0) were included, a striking correspondence between the simulated pattern of maximum stagnation pressures — defined by — and the recorded damage was found (Fig. 3). No tuning of parameters or initial conditions was made and a grid with 80 × 30 × 40 cells was used. Encouraging as it is, the success of this simulation must not be overvalued, because the uncertainties in the initial conditions are considerable and further tests under different conditions are needed to confirm the predictive power of the model.

Fig. 3. Powder-snow avalanche near Adelboden (Switzerland). Upper figure: results of a field investigation (from Reference Issler, Gauer, Schaer and KellerIssler and others, 1996). Lower figure: areal distribution of maximum stagnation pressures from a numerical simulation by Gauer. In the area with pressures in the range 3–5 kPa, the forest was completely destroyed, whereas only occasional trees were broken near but within the 1 kPa line. The basic topographic pixel maps are Swiss Federal Office for Cartography; reproduced with permission.

In the next step of model development, the full two-layer model is being coded in a depth-averaged version that can be applied to problems with relatively simple topography and for studying the behaviour of the coupled system before the computationally much more demanding three-dimensional version is elaborated. That work will be described elsewhere.

5. Conclusions and Outlook

The model described here is significantly more complex in its mathematical structure (not so much in numerical effort) than models in use today. A final assessment of what has been gained hereby has to await full numerical implementation and an extended series of validation runs. Nevertheless, a few preliminary conclusions can be drawn:

Further model development should address several points, namely (i) a more stringent mathematical formulation of the jump conditions at the layer interfaces, (ii) application to a significant number of well-known cases in order to understand better the dynamic behaviour of this coupled system, (iii) detailed modelling of saltation trajectories — including particle impacts — and their back-reaction on the air flow for a more precise determination of the model coefficients and (iv) coupling to a DFA model to study PSA formation.