Introduction
Mechanical properties of sea ice are highly dependent on air porosity as well as brine porosity (e.g. Weeks and Assur 1967, Schwarz and Weeks 1977). The latter has been investigated extensively in relation to salinity and temperature (Reference AssurAssur 1958, Reference AndersonAnderson 19601, but studies on air porosity are limited (Reference KusunokiKusunoki 1958). Results of mechanical tests on sea ice have been analyzed mainly to ascertain the influence of brine porosity or brine volume, neglecting the effects of air voids (e.g. Schwarz and Weeks 1977), although the dependence of mechanical properties on air porosity has been indicated (Reference TabataTabata 1958).
Two different approaches have been suggested for determining the air porosity of a sample of sea ice. One approach is to compare the measured density of the sample with the theoretical density for air-free sea ice (Anderson I960, Reference OnoOno 1968). Another approach is by direct measurement of the volume of air which is released through melting, assuming that air bubbles in the sample are at atmospheric pressure (Reference KusunokiKusunoki 1958, Savel’yev 1954).
Both approaches involve several problems that must be clarified. In the former approach, there are uncertainties in the values of physical quantities used for calculating the theoretical density for air-free sea ice (e.g. density of brine). In the direct measurement of air released, the air-bubble pressure is uncertain. A pressure higher than one atmosphere could be generated in air bubbles as the temperature at a given depth decreases with increasing thickness of an ice cover. In addition, one has to determine the amount of dissolved air in meltwater that must be added to the amount of liberated air to obtain the real volume of entrapped air. Applying a similar method to measure the air content of glacier ice, Reference LangwayLangway (1958) found that the meltwater was almost saturated with air. For sea ice, however, the saturation ratio for meltwater could not be near complete saturation, since the air content of sea ice is expected to be smaller than for glacier ice.
In this paper, experimental results on the saturation ratio of air in meltwater are presented, and estimations of porosity by the two methods are compared, using data obtained on first-year sea ice from the Arctic.
Collection of Air Entrapped in an Ice Sample
The air entrapped in an ice sample can be collected by melting the sample, thus releasing the air. As early as 1925, Arnol’d-Áliab’yev suggested a simple apparatus for collecting the air and measuring its volume: released air is introduced into a burette through a bottomless bottle (Savel’yev 1954). This type of apparatus was used by Reference KusunokiKusunoki (1958) for measuring the amount of air in very thin sea ice (<0.2 m thick), where a relatively large amount of air was expected. Although a similar amount of air is likely in the upper portion (say above 0.2 in in depth) of a first-year sea-ice cover in the Arctic, the deeper portion is considered to contain much less. The Arnol “d-Aliab’yev system, with a burette, would probably not be accurate enough to measure the small amount expected. A method developed by Reference NakayaNakaya (1956), therefore, was adopted for collecting the air released by melting and measuring its volume.
The apparatus is shown schematically in Figure 1. An ice sample was put into a container of kerosene in a cold room. A watch glass was placed over the sample and the whole system was brought into a warm laboratory. As the ice melted, air in the sample was released and trapped under the watch glass. The level of kerosene was adjusted to be close to the top of the watch glass so that the pressure of the trapped air would be the same as the measured air pressure of the laboratory. The temperature of the kerosene was measured by a thermocouple at a point close to the trapped air.

Fig. 1. Experimental Apparatus For Determining Air Content.
The captured air under the watch glass took a form similar to an oblate spheroid and was circular in the horizontal plane. The diameter of the circle was measured using a travelling microscope, and the diameter converted to volume of air by means of the equation given in Figure 2, which was obtained by injecting air of known volume under the watch glass.

Fig. 2. The relation between diameter ø and volume v of trapped air under the watch glass.
Dissolved Air in Meltwater
The dissolved air in meltwater was estimated as follows. Blocks of air-free columnar-grained ice were grown in the laboratory (Reference GoldGold 1972). Specimens of 40 to 70 g in weight (the same range as for the sample for porosity measurements, described in the next section) were prepared and holes were made with a drill from one side of each block. A piece of ice was frozen to this side after drilling. The volume of the cavities thus prepared was determined by measuring their dimensions with a travelling microscope. For some blocks, the porosity (the volume of the cavities) was estimated by measuring the density accurately with a procedure described by Reference NakawoNakawo (1980). These blocks with cavities of known volume were melted in kerosene as described in the previous section. The volume of air released from the blocks and captured under the watch glass was always smaller than the pre-determined vol une of the cavities. The difference was considered to be the amount of air dissolved in the meltwater.
During the experiment, the volume of the captured air (horizontal diameter of the air) was found to decrease continuously with time. This decrease indicates that air can be absorbed by the kerosene, even though the solubility of air in kerosene is very small. The captured air under the watch glass, therefore, can diffuse toward the meltwater or toward the atmosphere. The latter could take place because the concentration of air in kerosene would be larger near the trapped air than at the planar top surface of kerosene because of the effect of curvature. When air was injected under the watch glass when no water was underneath, however, no decrease in the volume of the trapped air was observed for a couple of days. It is considered, therefore, that the amount of air escaping to the atmosphere is negligible, and that the movement is primarily to the meltwater, increasing its saturation ratio.
With this assumption, the air content of the meltwater was calculated from the difference in volume between the cavities in an ice block before melting and the captured air under the watch glass after melting. Because the volume of the captured air kept decreasing as described above, the air content of the meltwater was assumed to increase with time.
An example of the results of this experiment is shown in Figure 3, in which the. temperature is also presented. The abscissa in the figure is the time when the whole system was brought from the cold room to the warm laboratory; t0 and te indicate respectively when the ice block melted completely and when the kerosene temperature at a point close to the captured air came to room temperature. The kerosene temperature was 15°C even before the ice had melted completely, and subsequently reached the equilibrium value very rapidly. It took a longer time, however, for the saturation ratio to reach equilibrium (complete saturation). The air content of meltwater was only about 20 and 30% by volume of its saturation value at t0 and te, respectively, in this example.

Fig. 3. Time variation of air saturation ratio in meltwater and kerosene temperature.
When the total surface area of the air cavities is large, there could be a greater possibility during melting for air to dissolve into the meltwater. The degree of air content of the meltwater at a given time, therefore, could be a function of the total surface area of the cavities, and hence a function of cavity size and bulk porosity. In order to examine this, 23 blocks having different porosities were prepared using different size drills. Following the above procedure, air saturation at to and te was calculated for these blocks.
The results are shown in Figure 4. Two data points connected by a vertical bar correspond to each block, and the lower point represents the value at t0 and the higher point at te. Drill size is differentiated by different symbols. It can be seen that air saturation increased with increasing porosity for the same size of cavity. Blocks with finer cavities prepared by smaller drills resulted in a larger degree of air saturation in the meltwater in comparison with those blocks having large cavities with the same porosity. The two fine solid lines in Figure 4 are “eye fit” curves for the smaller two drill sizes (0.65 and 0.9S mm) and the larger sizes (3.90 and 6.00 mm). The small difference in drill size did not give a significant difference in the air saturation, although any change in hole size changes the surface area of the cavities. The scatter of the data for the curves is about ± 5% by volume, which would cause an uncertainty of about 0.15% in porosity.
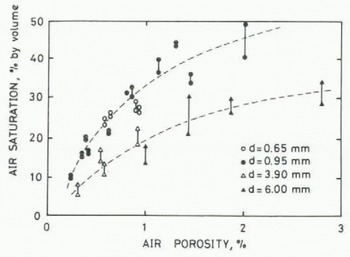
Fig. 4. Dependence of air saturation on air oorosity and drill size.
For estimating the air saturation ratio in melt-water by using the calibration curve given in Figure 4, one has to know the average size of air bubbles and bulk porosity of the sample. The former can be obtained by observation. Since the latter is the term that one is trying to determine, an iteration method has to be employed. Assuming the tentative porosity value to be given only by the volume of collected air, the air saturation ratio in meltwater is obtained using a curve in Figure 4. By adding the amount of dissolved air thus obtained to the volume of collected air, the second tentative value for air porosity of the sample is obtained. This process can be repeated until the value for the porosity converges. It is assumed, in the above calculation, that air bubbles in an ice sample are at one atmospheric pressure.
Salinity, Dehsitr, and Air Porosity
Sample description
Two core samples, 75 mm in diameter, were recovered from first-year sea ice at Eclipse Sound, near Pond Inlet, Baffin Island, Canada. The coring was done on 31 fiaren 1980, when the air temperature was about -23°C. The recovered cores were 0.740 and 0.795 m in length. They were brought back to the main camp at Pond Inlet, where the shorter core (core 1) was analyzed the following night. The longer core (core 2) was packed with dry ice and shipped to Ottawa for the later analyses, which were carried out after storage for six months at a temperature of -40°C.
In the winter of 1979-80, the freeze-up date was 16 October 1979. The growth of the ice in the early part of the season was similar to that of other winter seasons: the growth rate of sea ice was in the order of 0.2 μm s−1 (1.7 cm d−1) with rate decreasing with time In early November, however, when the thickness of the ice had reached about 0.3 m, snow of about 0.3 m depth was deposited on the ice, and stayed until the melting season started. The presence of the thick snow layer throughout the winter, except for the early period, contrasted with the situation in other winters. The growth rate of the ice decreased dramatically to about 0.05 μm s−1 (0.4 cm d−1) after the snow came, i.e. for ice below 0.3 m in depth. The growth rate was almost constant around the lower value (0.05 μm s−1) during the winter season. The thermal conductivity of snow is smaller than that of ice by an order of magnitude, and a snow layer of 0.3 m thickness is equivalent in thermal insulation to sea ice of about 3 m thickness. It is considered that the almost constant growth rate in the winter is due to the fact that the insulation effect of sea ice, which increased with time, is very small in comparison with the large insulation effect of the thick snow layer, which did not vary significantly with time.
A continuous columnar-grained ice was found below about 0.2 m depth level.
Measurements and results
A similar procedure’ was followed in determining salinity, density, and air porosity for both the ‘in field measurements (core 1) and the laboratory measurements (core 2). The cores were sectioned into segments of either 50 mm (core 1) or 25 mm (core 2). The radial surface of each segment was trimmed, resulting in the final weight of each sample being between 40 and 70 g. Mass, volume, and density were determined accurately using a hydrostatic method, in which the samples were weighed both in air and 2,2,4-trimethyl-pentane (Reference NakawoNakawo 1980), Measurements were made at about -15°C for core 1 and at about -28°C for core 2. The accuracy of the density measurement was ±0.4 to ±0.8 kg m−3.
In the estimate of porosity, the curve for the smaller two sizes (0.65 and 0.95 mm) of drill shown in Figure 4 was adopted for calibrating the dissolved air in meltwater, since most of the air bubbles in the samples were approximately 0.5 to 1.0 mm in diameter. Large bubbles of 2 to 3 mm in diameter were found as well as the smaller bubbles in the samples from 0 to 0.2 m depth. Using the curve for the smaller sizes of cavities could result in overestimating dissolved air in meltwater for these samples. The amount of air collected from the shallow samples, however, was much larger than the amount of dissolved air, even for the condition of air-saturated meltwater. The final porosity value, therefore, was not influenced significantly by the overestimation.
After the measurements on porosity, the resulting meltwater was used for the salinity measurement by a refractometer/salinometer. A simple experiment, which was carried out before the measurements, indicated that a small amount of kerosene in the water would not affect the salinity readings. It was difficult, however, to take a reading when a larger amount of kerosene was present and so care was taken to remove as much as possible from the meltwater. Although it was not possible to eliminate it completely, the remaining kerosene was not significant.
The results of the measurements on salinity, air porosity, and density are shown in Figure 5(a) for core 1 and in (b) for core 2. It was found that both sets of data agree with each other. The salinity decreased gradually from the top to about the 0.3 m depth level, stayed almost constant through the body of the ice cover, and increased sharply at the lower surface. A similar profile can be seen for air porosity, indicating a positive correlation between the two quantities. The vertical profile of density, on the other hand, appears to exhibit an inverse proportionality between density and salinity or air porosity, i.e. the small density corresponds with the large salinity and air porosity, and vice versa.

Fig. 5. Vertical profiles of salinity, density, and air porosity for core samples of first-year sea ice. (a): in situ measurement at -15°C (core 1). (b): laboratory measurement at -28°C after 6 months of storage at -40°C (core 2).
Discussion
From the density values measured, air porosity was calculated by comparing with the theoretical density for air-free sea ice (Anderson I960). The value for the theoretical density was obtained from the salinity value for each segment and the temperature (-15°C for core 1 and -28°C for core 2). The air porosity values thus obtained are compared with those from the direct measurements in Figure 6. They are in good agreement, indicating that air bubbles are approximately at atmospheric pressure, although the assumed theoretical density values still cause some uncertainty, as described in the introduction.

Fig. 6. Comparison of air porosity between the values from density measurement and from the direct measurement of air content.
It was impossible to prevent the initial brine drainage completely when the cores were recovered from the ice. Air could have been introduced into some of the brine channels at that time, which would have the effect of making the apparent average bubble pressure closer to the atmospheric pressure.
The measured salinity of about 0.3% in samples below 0.3 m depth, for which the growth rate was about 0.5 μm s−1, is smaller by 0.1% than the value expected for the growth rate from a regression curve given by Nakawo and Sinha (1981), which was based on a series of observations made soon after core samples were recovered. This salinity difference, therefore, could be due to desalination during storage. Ice temperature for the 1979-80 winter, however, was extraordinarily high, owing to the thick snow layer on the ice. Substantial natural desalination, therefore, could have taken place before core recovery in this particular winter. Additional brine drainage during storage (from the core recovery to the time of the measurements) is considered to have been small, because the period was short, about 10 h, for core 1 and the storage temperature was low, -40°C, for core 2.
In addition to the effect of desalination, mechanical relaxation could also cause decrease of the bubble pressure, even if it were at a higher pressure than one atmosphere. A simple calculation indicates, however, that it takes longer than a year for the pressure to decrease from several atmospheres to near one atmosphere. Thus, the relaxation effect is considered to be negligible.
The bubble pressure, therefore, is considered to be near one atmosphere in the ice, some uncertainty being caused by the initial brine drainage that may have taken place when the cores were removed. Samples of sea ice to be used for mechanical tests are usually subject to the same problem: it is difficult to avoid the initial brine drainage completely. For such samples, at least, the air bubbles can be considered to be at atmospheric pressure. This implies that air porosity can be determined from either density measurements or direct measurement of air volume,
Salinity has a strong correlation with growth rate (Cox and Weeks 1975, Nakawo and Sinha 1981). Air porosity also could be dependent on growth rate. If a relation between them is known, and with information on growth rate only, three important factors that affect mechanical properties can be estimated, i.e. salinity, density, and air porosity, since density is a function of salinity and air porosity. Reference CarteCarte (1961) and Bari and Hallett (1974) have investigated experimentally the dependence of air content of ice on growth rate, but their growth rates are too large to be used for naturally grown ice.
The present results shown in Figure 5 suggest a dependence of air porosity on growth rate, the porosity decreasing with decreasing growth rate (0 to 0.3 m), and almost constant air porosity for constant growth rate (0.3 to 0.8 m). A correlation analysis, however, was not made as the growth process was considered to vary with time near the surface of the ice, as was indicated by the crystallographic texture exhibited in a thin vertical section, and there was little variation in growth rate in the lower, continuous columnargrained structure. It would be interesting to obtain a vertical profile of air porosity in sea ice having a continuous columnar-grained structure for which the growth rate varied significantly.
Acknowledgements
The core recovery and the in situ measurements were made with the help of Steltner Development and Manufacturing Company Ltd. The author wishes to thank H A R Steltner for arranging those activities, and S Koonoo, M Komangapitc, and E Pewaotulook for technical assistance in the field. The author is also indebted to Dr H K Sinha and to D Wright of the Division of Building Research, National Research Council of Canada, for encouraging him throughout the work and for technical assistance in the laboratory measurements.
This paper is a contribution from the Division of Building Research, National Research Council of Canada, and is published with the approval of the Director of the Division.








