1. Introduction

As shown in numerous studies, glacier mass balances are good indicators of climate change in tropical areas where historical climate data are rare (Dyurgerov, 2002; Reference Coudrain, Francou and KundzewiczCoudrain and others, 2005; Reference Sicart, Wagnon and RibsteinSolomon and others, 2007). According to the astronomical, thermal, and hygric delimitations proposed by Reference KaserKaser (1999), approximately 99% of tropical glaciers are located in the highlands of the intertropical belt of South America. The others are located in East Africa and New Guinea (Reference HastenrathHastenrath, 1984, Reference Hastenrath1995; Reference Kaser, Hastenrath and AmesKaser and others, 1996; Reference KaserKaser, 1999).

Moreover, mass-balance studies of glaciers in South America are essential to estimate the quantity of water available for future human consumption and hydropower generation. The assessment of water resources can help minimize the economic impact of the retreat of these glaciers (Reference SolomonVergara and others, 2007). Consequently, knowledge of the climatic parameters controlling glacier mass balances is of prime importance to understand the response of tropical glaciers to the specific climate forcing over the intertropical zone. For this purpose, long-term mass-balance data are needed.

In Bolivia, a long-term glaciological program has been carried out since 1991 by the Institut de Recherche pour le Développement (IRD), France, (Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995; Reference RamírezRibstein and others, 1995) and in the framework of the French glacier monitoring program GLACIOCLIM (http://www-lgge.obs.ujf-grenoble.fr/ServiceObs/index.htm). The objective of this program was to survey two glaciers: Glaciar Zongo and Glaciar Chacaltaya. Given the imminent disappearance of Glaciar Chacaltaya (Ramirez and others, 2001), another glacier monitoring program was started on Glaciar Charquini Sur (Reference RabatelRabatel, 2005; Reference Rabatel, Machaca, Francou and JomelliRabatel and others, 2006) in 2002. These glaciers were selected mainly because of the influence of ice melting on water resources for human consumption and hydropower generation for the city of La Paz.

Two independent methods have been used to assess these glacier mass balances using glaciological data (Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995) and hydrological data (Reference RamírezRibstein and others, 1995). In addition, numerous studies have been carried out to assess the relative importance of melting and sublimation in the energy balance (Reference VergaraWagnon and others, 1999a) in order to understand the relationships between energy balance and glacier runoff (Reference VincentWagnon and others, 1999b) and to provide insight into the atmospheric control of the energy balance (Reference Ribstein, Pouyaud, Sicart, Wagnon, Ramirez and FrancouSicart and others, 2005). Moreover, hydrological investigations have been performed to compare mass-balance results from the glaciological and hydrological methods (Reference SicartSicart and others, 2007).

Differences between the glaciological and hydrological methods were first pointed out by Reference Francou, Ribstein, Saravia and TiriauFrancou and others (1995) and attributed to ice sublimation in the dry season. Later, this assumption was rejected by Reference SicartSicart and others (2007), who assumed that sublimation was too small to explain the discrepancies. Reference SicartSicart and others (2007) concluded that the hydrological method gives values that are approximately 0.6mw.e.a^–1 lower than the glaciological method. According to these authors, the large difference between the two methods was due to the catch deficiency of rain gauges and the lack of precipitation measurements at high altitudes around Glaciar Zongo.

However, neither method can estimate accurately the overall accumulation rate in the accumulation zone of the glacier. On the one hand, the glaciological mass balance is calculated from only two or three snow pits. On the other hand, the highest rain gauge used to calculate the hydrological mass balance is only 5200ma.s.l. and the accumulation rate inferred from these data can be questioned. Moreover, the accumulation zone corresponds to about 60% of the total area. Consequently, the uncertainty for both methods is large (Reference SicartSicart and others, 2007) and these data cannot be used to accurately determine the mass balance of Glaciar Zongo.

The first purpose of our study is to assess the cumulative glacier mass balance from an independent method using photogrammetric data. This geodetic method has been widely used to check cumulative mass balances (Reference Thibert, Blanc, Vincent and EckertVincent, 2002; Reference Bauder, Funk and HussBauder and others, 2007; Reference Sicart, Ribstein, Francou, Pouyaud and CondomThibert and others, 2008). These new data make it possible to compare glacier mass balances from the glaciological method (1991–2006), the hydrological method (1974–2006) and the geodetic method (1956–2006). The second purpose is to extend the mass-balance time series into the past using both hydrological and photogrammetric data.

2. Location

Glaciar Zongo is located in the Huayna Potosi region (Cordillera Real, Bolivia; 16˚ S, 68° W), 30 km north of La Paz, between the dry Altiplano plateau in the west and the wet Amazonian basin in the east (Fig. 1). Most of the precipitation comes from the Amazonian basin. The glacier is temperate (Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995) and covers an area of 1.96 km² over a hydropower catchment area of 3.3 km². Its length is 3000 m and its width is 750 m. The glacier flows from 6100 to 4900ma.s.l. The average ice-flow velocity is 20 ma^–1 between 4900 and 5200 ma.s.l.

Fig. 1. Contour map of Glaciar Zongo showing the surface topography in 1983 with 20 m contour intervals and the terminus of the glacier in 2006.

Meteorological conditions in the intertropical belt have been thoroughly analyzed by Reference Kaser, Hastenrath and AmesKaser and others (1996) and Reference KaserKaser (2001), and two distinct areas can be distinguished: (i) inner tropics, with almost no seasonality in precipitation and (ii) outer tropics, with strong seasonality in precipitation. These meteorological differences have a strong impact on glacier surface mass balance. In the inner tropics, both accumulation and ablation occur throughout the year. In the outer tropics, accumulation and ice/snow melt occur mainly during the wet/summer season. During the dry/winter season, ice/snow melt is reduced and ice/snow sublimation is significant (Reference KaserKaser, 2001; Reference Favier, Wagnon and RibsteinFavier and others, 2004). Glaciar Zongo is located in the outer tropics area (Reference VergaraWagnon and others, 1999a; Reference Favier, Wagnon and RibsteinFavier and others, 2004). Average precipitation, temperature and runoff are shown in Figure 2.

Fig. 2. Climatic conditions of the outer tropical Glaciar Zongo. The black curve shows the mean monthly runoff (1973–2006), the grey curve shows the mean monthly precipitation (P4750; 1971–2006) and the dashed curve shows the mean monthly temperature (El Alto station; 1968–2006).

3. Data and Methods

The mass balances of Glaciar Zongo have been reconstructed since 1956 using glaciological, hydrological and geodetic data. According to the wet/dry seasons, the hydrological year has been fixed between 1 September and 31 August (Reference RamírezRibstein and others, 1995). Only a short description of each method is given since the methods have been thoroughly described in previous papers (Reference RamírezRibstein and others, 1995; Reference SicartSicart and others, 2007).

The glaciological method estimates the loss or gain in mass over the whole glacier surface from field measurements obtained from stakes in the ablation area and snow pits/drilled cores in the accumulation area (Fig. 1). The specific mass balance of the glacier is obtained using the traditional glaciological method (Reference PatersonPaterson, 1994). Annual mass balances have been calculated with this method over Glaciar Zongo since 1991, using 14 stakes for monthly measurements and 3 snow pits/drilled cores for yearly measurements averaged over the ablation and accumulation zones respectively (http://glaciog.ujf-grenoble.fr/ServiceObs/SiteWebAndes/index.htm). Provided that snow accumulation can occur at any time during the year in the ablation area, snow height measurements are required together with stake emergence measurements. Unfortunately, snow height in the ablation area was not always measured between 1991 and 2001, which could lead to greater uncertainties in annual mass balance over this period. For these measurements in the ablation area, the snow and ice density were assumed to be 400 and 900 kgm^–3 respectively (Reference Francou, Ribstein, Saravia and TiriauDyurgerov, 2002). In the accumulation area, snow-pit/drilled-core measurements were carried out at least once a year at the end of the hydrologic year. The snow density was measured for each pit. Until now, the surface area used to calculate the specific mass balance of Glaciar Zongo came from a 1983 map (Fig. 1) without taking into account the decrease in surface area (Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995; Reference SicartSicart and others, 2007). Consequently, it was assumed that the influence of area reduction since 1983 was not significant. As can be seen below, this assumption is not supported by photogrammetric data.

For these reasons, the 15 annual mass balances of Glaciar Zongo (1991–2006) were recalculated for our study. The main changes involve the ablation area. First, the snow heights were roughly estimated in the ablation area for the 1991–2001 period when the snow layer persisted at the end of the hydrological year. These estimates were made using monthly mass-balance measurements (stake emergence measurements). No change was made in the accumulation area. Second, the assumption of constant surface area was rejected and the specific mass balance was computed using the actual surface areas. For this purpose, areas for different altitude ranges were calculated each year using detailed maps from photogrammetric data (see below). These two errors have been corrected, leading to changes in mass balance of 0.11 and 0.23mw.e. a^–1 respectively over the period 1991–2006.

The second method of obtaining mass balance is based on hydrological data. The hydrological mass balance is obtained from precipitation, glacier runoff and sublimation. The hydrological mass balance (b _n,H) is given by b _n,H = P–1/S _g [D–(S–S _g)c _e P]–E (Reference SicartSicart and others, 2007), where S _g is the glacier surface area (m²), S is the total surface area of the basin (m²), c _e is the runoff coefficient, P is the precipitation (m a^–1), D is the runoff at the outlet of the basin (m³ a^–1) and E is the sublimation of the glacier (m a^–1). Precipitation and the runoff of Glaciar Zongo were measured over two periods. From 1973 to 1991, precipitation (rain gauge P4750, at 4750ma.s.l., 1 km away from the glacier tongue with an opening area of 314 cm²) and runoff were measured twice a day (at 0700 and 1500 h) by the Bolivian Hydropower Company (Cobee). When the glaciological program started in 1991, a network of five additional rain gauges (opening area of 2000 cm²) was set up and was read monthly around Glaciar Zongo together with an automated stream gauge at the outlet of the Zongo basin. Comparison between P4750 and the rain gauge network around the glacier shows that rain gauge P4750 underestimates precipitation around the glacier by 20% (Reference Francou, Ribstein, Saravia and TiriauFrancou and others, 1995) and over the glacier by 29% (Reference SicartSicart and others, 2007). Additional precipitation measurements, from a Geonor pluviometer set up in 2003, reveal that P4750 underestimates precipitation by 37%. To estimate the hydrological mass balance of Glaciar Zongo, we used the daily rain gauge (P4750) to assess the accumulation rate between 1973 and 2006 and a positive correction of 37%. In addition, a runoff coefficient (ratio of runoff to precipitation) of 0.8 was used for the surface area not covered by the glacier (Reference RamírezRibstein and others, 1995, 1999; Reference SicartSicart and others, 2007). The water flow is deduced from the stream gauge measurements between 1973 and 1991 and from the automated stream gauge measurements between 1991 and 2006. To estimate monthly sublimation (E), we used monthly values of US National Centers for Environmental Prediction (NCEP)–US National Center for Atmospheric Research (NCAR) reanalysis data (Reference KalnayKalnay and others, 1996) from the gridcell closest to Glaciar Zongo (16° S, 68° W) at 500 hPa (around 5500ma.s.l.) and an empirical relationship (Reference FavierFavier and others, 2008) given by E=α(q–q _s)u (mmw.e. month^–1) where q, q _s and υ are the re-analyzed NCEP–NCAR data for specific humidity (gkg^–1), saturated specific humidity (gkg^–1) and horizontal wind speed (ms^–1) respectively, and α is a coefficient for homogeneity of the empirical relationship ( Reference FavierFavier and others, 2008). This coefficient has been calibrated with monthly sublimation data measured in the field from automatic weather stations by Reference Wagnon, Ribstein, Francou and PouyaudWagnon and others (2001) (September 1996–August 1998) and Reference Ribstein, Tiriau, Francou and SaraviaSicart (2002) (September 1999–August 2000 except for a data gap in March 2000). The correlation r ² over the 35 month period is 0.71, and yields a value for α of 0.694. The catchment and glacier areas were properly determined from photogrammetric data.

The third and independent method used to assess glacier mass balance comes from geodetic data. It can be used to calculate the volume change and, consequently, the cumulative mass balance of the glacier using digital photogrammetric data. Six photogrammetric flights have been carried out over Glaciar Zongo on 20 May 1956, 21 June 1963, 23 July 1975, 20 June 1983, 20 April 1997 and 13 July 2006 by the National Service of Aerophotogrammetry, Bolivia (SNA). The resulting photographs were scanned with a resolution of 14 μm using a photogrammetric scanner (Vexcel UltraScan 5000). In order to orient the images, a stereo preparation was performed in 2006 using the geodetic differential global positioning system (GPS) on ground-control points. Since the photographs had been taken earlier, obvious features were used as control points. Moreover, as the relative orientation of the images between two dates is more important than the absolute ground orientation, at least 25 tie points were added per stereo pair to improve consistency (Reference KruckKruck, 2002). The photogrammetric restitution was performed using a Leica digital system (Orima and LPS®) following an irregular grid: every 20 m on flat surfaces of the glacier and as low as every 5m in bumpy areas. Approximately 10 000 points were measured for each aerial campaign, over the whole area of the glacier (average area 2.2 km²). The average measurement accuracy is 7.5 mm for photograph coordinates and 0.64m for ground-control point coordinates. Some areas with low contrast or shadows were not measured (shown in white in Fig. 3) The digital elevation models (DEMs) were constructed using Surfer software with a grid of 10 ×10 m and a minimum curvature algorithm. The algorithm employed for DEM construction has a weak impact on the whole glacier volume (Reference Sicart, Wagnon and RibsteinThibert and others, 2008). The subtraction of the DEMs yields variations of surface elevation that must be converted to water equivalent using the ice density, i.e. 900 kgm^–3 (see section 5).

Fig. 3. Thickness variations (m) of Glaciar Zongo over the periods 1956–63, 1963–75, 1975–83, 1983–97, 1997–2006 and 1956–2006. The color scale is the same in each case. The white areas corresponding to shadowed or low-contrast areas were not measured. The surface areas of Glaciar Zongo are 2.29, 2.31, 2.26, 2.23, 2.12 and 1.96 km², corresponding to 1956, 1963, 1975, 1983, 1997 and 2006 photogrammetric flights respectively.

4. Results

The geodetic method gives the long-term cumulative mass balance. Based on photogrammetric measurements, digital maps were plotted for 1956, 1963, 1975, 1983, 1997 and 2006, and thickness variations were calculated from these data over the corresponding periods (Fig. 3). Some global features can be observed. Over the first period (1956–63), changes in volume are small, while the second period (1963–75) displays a positive volume variation in the highest part of the glacier. The period 1975–2006 shows a strong change of volume in the ablation zone. Over the whole period 1956–2006, a gradual loss of volume is observed in the ablation zone, with no significant changes in the upper part of the glacier. Finally, the cumulative mass balance of Glaciar Zongo calculated over the last 50 years using photogrammetric and hydrological methods is displayed in Figure 4 and Table 1. The figure reveals a striking agreement between independent data obtained by the hydrological and photogrammetric methods. The cumulative glaciological mass balances are also plotted in Figure 4 and shown in Table 1. However, as explained in the next section, these glaciological results have been adjusted according to the photogrammetric data.

Fig. 4. Zongo cumulative mass balance (mmw.e.) calculated by the geodetic method (black triangles), the hydrological method (grey curve) and the glaciological method (black curve). The hydrological mass balances were obtained from annual data between 1974 and 2006. The glaciological mass balances were calculated using yearly field measurements and adjusted according to photogrammetric data. The origin of the hydrological mass balance is the geodetic value in 1975. The hydrological mass balance envelops correspondents to one standard deviation (thin grey curves). Glaciar Zongo lost 16.32 mw.e. in mass between 1956 and 2006 and 15% of its surface area between 1956 and 2006. It seems that between 1956 and 1975 the glacier was near steady-state conditions. Conversely, the periods 1975–83 and 1997–2006 show strong negative mass-balance rates of –0.91 and –0.84mw.e. a^–1 respectively.

Table 1. Zongo cumulative mass balance (mw.e.) calculated by the hydrological, glaciological and geodetic methods

5. Discussion

The mass balance of Glaciar Zongo has been assessed using three independent methods. Uncertainties related to each method are analyzed below.

The comparison between glaciological and hydrological mass balance reveals a large discrepancy over the period of the common data, i.e. 1991–2006. The cumulative mass balances resulting from the two methods diverge by 7.4 mw.e. over the 15 years of observations.

To try to explain this discrepancy, glaciological surface mass-balance data from stake and pit measurements were analyzed. Three areas of 4 ha were selected in the ablation area at 5050, 5100 and 5150 ma.s.l., and three others in the accumulation area at 5550, 5650 and 5750ma.s.l. These areas correspond to surface mass-balance field measurements covering the entire period. In each area, centered mass balances were calculated by subtracting the average mass balance from the annual values (Fig. 5a). The figure shows striking consistency for the data obtained from the ablation area, despite the high variability. The relationships between surface mass balance in the ablation area are strong, with correlation coefficients between r ² = 0.92 and r ² = 0.86. This confirms the validity of the surface mass-balance data in this area. Figure 5a also shows the large variability difference between the accumulation and ablation areas. The standard deviations are high for the elevation ranges of the ablation area (σ = 1.6, 1.5 and 1.4mw.e. a^–1 for elevations 5050, 5100 and 5150m respectively, over the period 1991–2006) and are low for the elevation ranges of the accumulation area (σ = 0.5, 0.4 and 0.4mw.e. a^–1 for elevations 5550, 5650 and 5750 m respectively, over the period 1991–2006). Figure 5a suggests that specific mass-balance change is mainly controlled by the ablation area. Over the whole glacier area, the standard deviation ranges roughly from 1.6mw.e. a^–1 in the ablation area to 0.4mw.e. a^–1 in the accumulation area. Assuming constant surface areas, the variance of the specific mass balance is given by , where S〉 and σ〉 are the surface area and surface mass-balance standard deviation of elevation range i, and S is the surface area of the glacier (〉 = 1,...). Over the period 1991–2006, the surface mass-balance standard deviation is estimated to be –0.75mw.e. a^–1, although it cannot be determined properly over several elevation ranges. The values can be used to assess the relative contribution of each elevation range 〉 to the specific mass-balance change for 1 year. The very large contribution of low-elevation ranges to the specific mass balance is apparent: over the period 1991–2006, more than 80% of the variance comes from elevation ranges below 5300 m, representing roughly one-third of the total surface area. The contribution of the tongue changes in time with the area changes. For instance, the mass-balance changes between 4900 and 5200m accounted for about 73% of the specific mass-balance change in 1991, although the surface area was 25% of the glacier. This contribution fell to 24% in 2006 following the area reduction. The centered specific mass balances are plotted in Figure 5b, using glaciological and hydrological data. Despite large unexplained discrepancies in 1999, fluctuations of the two sets of mass-balance data are consistent, with a correlation coefficient of r2 = 0.80.

Fig. 5. (a) Centered annual surface mass balance (mw.e. a^–1) for different elevation ranges; and (b) centered specific mass balance (mw.e. a^–1) obtained from glaciogical data and from hydrological data.

However, the difference between the average glaciological and hydrological mass balance remains. Provided that surface mass-balance measurements are reliable and that surface area changes have been properly taken into account, the discrepancy should come from the sampling network. It can be concluded that the field measurement sites are not representative of the entire area of the glacier and that the linear interpolation between surface mass-balance measurements from different elevation ranges (5250–5550 m) is not valid for calculating the specific mass balance. Consequently, to determine the specific mass balance, the glaciological data have been adjusted according to the photogrammetric data between 1997 and 2006. For this purpose, the average volumetric mass balance over this period has been added to the centered specific glaciological mass balance calculated over the same period (Fig. 4).

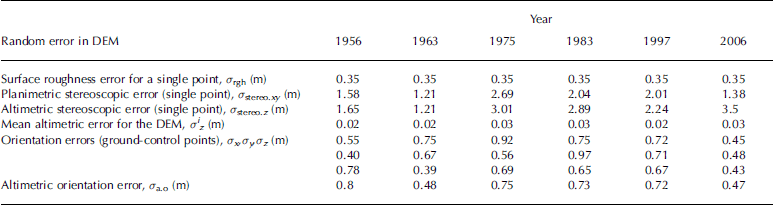
Error analysis of photogrammetric results was performed using the method of Reference Sicart, Wagnon and RibsteinThibert and others (2008) and is shown in Table 2. Additional uncertainties result from snow/ice density uncertainties and unmeasured areas resulting from lack of stereoscopic measurements. The overall error in the cumulative mass balance obtained from photogrammetric data is estimated at 2.0 mw.e. over the entire period 1956–2006. The uncertainty of the hydrological method is difficult to assess accurately. As shown by Reference SicartSicart and others (2007), the runoff discharge error is small, i.e. 5% in the range 0–600 L s^–1 (Reference RamírezRibstein and others, 1995). Additionally, provided that the portion of basin area free of ice is reduced, the influence of the runoff coefficient is small. The maximum changes in mass balance due to changes in the runoff coefficient from 0.5 to 1 are –0.20 and +0.15mw.e. (Reference SicartSicart and others, 2007). The average sublimation rate calculated over the last 50 years over Glaciar Zongo is 171 mmw.e a^–1. The uncertainty of this parameter is difficult to assess and it can be assumed that it is less than 0.1mw.e. a^–1. Therefore, the uncertainty of the hydrological mass balance depends mainly on the accumulation uncertainties. As mentioned by Reference SicartSicart and others (2007), no clear relationship can be found between altitude and precipitation. The field glaciological measurements show that the accumulation rate is low both in the ablation zone and in the accumulation zone (about 1mw.e. a^–1). It is assumed that the uncertainty in the accumulation rate calculated from precipitation should not exceed 0.2 mw.e. a^–1. As a result, the uncertainty of annual hydrological mass balance is 0.3 mw.e. a^–1 maximum and the overall error in the cumulative mass balance from hydrological data is estimated at 1.68mw.e. over the period 1975–2006 (Fig. 4). The very good agreement with photogrammetric data confirms that glacier mass balance obtained from hydrological data is reliable.

Table 2. Error analysis in the volumetric mass-balance measurements (see Reference Sicart, Ribstein, Francou, Pouyaud and CondomThibert and others, 2008, for details)

6. Conclusions

These glacier cumulative mass-balance results over the last 50 years are unique for this region. Hydrological data have made it possible to reconstruct annual glacier mass balance since 1974.

Only two other glacier mass-balance series have been investigated in the Cordillera Real over a similar period: those for the Charquini glaciers located 5 km from Glaciar Zongo, and Glaciar Chacaltaya 9 km away. The cumulative mass balance of the Charquini glaciers between 1956 and 1997 was assessed by Reference RabatelRabatel (2005) using photogrammetric data. Glaciar Charquini Sur (0.36km²; the glacier flows approximately from 5280 to 4985 ma.s.l.), with similar exposition, shows similar fluctuations over the whole period, with a strong negative mass balance of –0.79mw.e. a^–1 between 1975 and 1983.

The cumulative mass balance of Glaciar Chacaltaya (0.007km²; the glacier flows approximately from 5325 to 5225 ma.s.l.) has been roughly reconstructed between 1963 and 1998 using photogrammetric and stake-measurements data (Ramirez and others, 2001). The mean mass balance is very negative, –0.75mw.e. a^–1 over the whole period. Over the period 1983–98 this series shows a stronger negative mass balance of –0.96mw.e. a^–1. However, this glacier will disappear in the near future, and its specific mass balance was mainly controlled by the high surface-area change over recent decades.

As shown in other studies of tropical glaciers (Reference KaserKaser, 1999), the vertical budget gradient is high (∽2mw.e. (100 m)^–1). Furthermore, our study reveals strong temporal variability of the surface mass balance in the ablation area, more than twice the mean variability.

Mass-balance fluctuations derived from hydrological, glaciological and photogrammetric data agree well. However, the glaciological method reveals a strong bias in specific mass balance, as many areas cannot be sampled because of difficult access. The glaciological mass balance has therefore been corrected using photogrammetric results. The photogrammetric method is therefore needed to provide a reliable average specific mass balance over the whole period. Generally, the hydrological method depends strongly on the correction of the measured precipitation in the catchment area. However, for Glaciar Zongo it seems that accumulation changes are low and do not significantly influence hydrological mass-balance changes. Comparison between annual surface mass balances observed from stake measurements reveals very similar temporal changes and proves that surface mass-balance changes are strongly related to meteorological conditions. On the whole, the glacier was close to steady-state conditions between 1956 and 1963, between 1963 and 1975 it gained mass, and after 1975 the specific mass balance is negative. The strong temporal variability of the surface mass balance in the ablation area leads to a large influence of surface area reduction. The relative contribution of the tongue (between 5200m and the terminus) to the specific mass balance has decreased from 73% in 1991 to 24% in 2006.

As a result, the surface area of this glacier converges to steady state faster than glaciers in other regions of the world.