Background
Widespread avalanche activity often increases significantly a few minutes after the onset of rain on freshly deposited snow. These avalanches usually release as slabs several hours before liquid water and the associated thermal wave has penetrated to the sliding layer (Reference Conway and RaymondConway and Raymond, 1993). The abrupt change in stability following relatively small alterations that are restricted to the surface has been a puzzle. The failure layer is dry at the time of avalanching and it is unlikely that the increased avalanche activity is caused simply by the additional gravitational loading associated with the rainfall, because continued loading at the same rate but from snowfall does not usually cause such widespread and immediate avalanching. Apparently, snowpacks just prior to rain often exist in a metaslable condition and perturbations caused by the rain are sufficient to alter slope stability. Here, I present and discuss measured changes of mechanical and thermal properties at the onset of rain in the context of the observed rapid and widespread avalanche activity. I make use of an existing model of dry snow-slab failure to examine the impact of rain-induced alterations and use the results to infer pre-failure conditions in the snowpack.
Field Measurements
The study site is in the Cascade mountains near Snoqualmie Pass, Washington, U.S.A. where mid-winter rain on snow is common. In collaboration with avalanche technicians from the Washington State Department of Transportation, we have contiguous measurements of weather conditions (winds, air temperature and precipitation) and snow properties (layer stratigraphy, temperature and creep profiles). Some measurements are discussed below.
In-Situ Measurements of Creep and Temperature
Figure 1a shows the set-up used to measure creep and temperature profiles on slopes. Shoes made from light-weight aluminium screening were placed sequentially at the surface after accumulations of 0.1–0.3 m of snow. The vertical velocity profile was obtained by measuring the position of shoes that were constrained to slide down a fixed pole. A sliding contact mounted on each shoe made electrical contact with a resistance wire attached to the pole and time variations of the vertical position of each shoe were calculated from this voltage-divider circuit. Calibrated thermistors attached to the shoes were used to obtain temperature profiles. The non-vertical component of motion was measured by running a cord from a second shoe up-slope to a rotary potentiometer mounted on the vertical velocity shoe. Initially, the distance between pairs of shoes was set at about 1 m. Measurements were multiplexed and recorded at 5 minute intervals using a data logger and storage module. Shoe positions could be resolved with an accuracy of about ± 2 mm; temperatures were accurate to ± 0.01°C. The measurements were made near the middle of a 200 m long slope inclined at an angle of 36°. No avalanches released on the study slope while it was instrumented.

Fig. 1. (a) Experimental set-up used to measure creep and temperature profiles on slopes. (b) shows an example of creep profiles at 1 hour intervals starting at midday on 24 January 1993. Rain started at 15.00 h and many slab avalanches 0.55 m deep released on surrounding slopes soon afitet the rain started, (c) and (d) show shear strain-rate and temperature profiles 15 minutes after the rain started.
Figure 1b shows a typical example of creep measurements before and after a major rain-on-snow avalanche cycle. The material lines are drawn at hourly intervals and show the evolution of creep before and after rain which started at the site at 15.00 h on 24 January 1993. Rain, first on 22 December 1992 and again on 3 January caused the snow deeper than 0.55 m to settle and become relatively homogeneous. Snow, starting on 20 January, fell on a thin layer of faceted crystals. On sleeper slopes, several slab avalanches released at the faceted layer early in the storm but activity increased significantly and many slabs about 0.55 m deep released on all slopes soon after the onset of rain. Measurements show that most of the curvature in the creep profile was caused by differences in the rate of (vertical) settlement through the snowpack. The rate of motion decreased rapidly with density and large gradients in the velocity profile occurred because of contrasts in layer properties. Figure 1c and 1d show respectively the shear strain-rate and the temperature profile during the first 15 minutes following the onset of rain. Field observations of avalanche activity indicated that most slopes had avalanched by this time. During this first 15 minutes, the near-surface strain-rate was nunc than three times higher than that at depth (Fig. 1c) and only the surface snow had warmed to 0°C (Fig. 1d).The finite vertical spacing between the glide shoes and thermistors made it difficult to resolve all details of the profiles. It is likely that local strain rates were higher than those averaged values and that liquid water and the associated thermal wave had penetrated beneath the surface (although less than 0.12 m) at the time of avalanching.
This response to the first warming or welting of freshly deposited snow is typical. On horizontal snowpacks, we have measured similar rates of penetration of liquid water and the thermal wave (Reference Conway and BenedictConway and Benedict, 1994), and similar compactivc strain-rate profiles (Reference Conway and RaymondConway and Raymond, 1993). In addition, our stratigraphic measurements from snow pits soon after the onset of rain almost always show liquid water is contained within the upper 0.15 m of the snowpack. The degeneration of mechanical properties such as clastic modulus and fracture toughness with the introduction of liquid water is not surprising and the abrupt change in stability at the onset of rain is likely a response to both changes in the mechanical properties at the surface and additional loading from the rain. Below, I use existing models of snow properties and slope stability to evaluate the impact of these alterations.
Snow-Slope Failure
Stratigraphic observations and measurements at slab-avalanche fracture lines generally show a relatively thick cohesive layer of snow overlying a much thinner weak layer. Experimental evidence from Reference McClungMcClung (1977) shows that snow will strain-soften under favorable conditions of rapid shear deformation, which makes it appropriate to analyze conditions in terms of slip-weakening models in which the shear strength in a crack-like weak layer degrades with ongoing slip. Such models have been used successfully to describe instabilities along crustal faults caused by earthquakes (e.g. Reference Li and AtkinsonLi, 1987).
This approach was taken by Reference McClungMcClung (1979, Reference McClung1981), who studied two extreme cases for dry-slab failure: (1) the case where the applied shear stress was sufficient to cause a large area of the weak basal layer to soften, resulting in a dynamic propagating instability. These conditions might be expected during continued natural loading by snowfall. Rapid failure is expected as the applied shear stress approaches the peak strength of a thin, strain-softening basal layer (Reference McClungMcClung, 1979, Reference McClung1981). (2) the case where slip within the basal layer was non-uniform and stress concentrations acting at the edges of a small locally failed zone caused it to expand slowly until the limiting Conditions for rapid shear failure were met. in Nature, variations in both the driving stress (from changes in the slab thickness and/or density) and the resistance (from rather small changes in the structure and/or stratigraphy at the basal layer) could initiate non-uniform slip at the bed (Reference Conway and AbrahamsonConway and Abrahamson, 1984). Of course, the temporal evolution of the strength of the basal layer as a result of sintering or recrystallization of grains also has important controls on slope stability but that is beyond the scope of this paper.
McClung’s (case 2) analysis was based on a slip-weakening model from Reference Palmer and RicePalmer and Rice (1973), who showed that shear propagation of crack-like surfaces could be analyzed using an energy criterion. Figure 2 shows a schematic view of a slab overlying a zone of length 2L where the shear stress from the overburden is not fully supported. Propagation will occur if the energy released as the slab moves down-slope exceeds the energy necessary for plastic yielding at the crack tip. During deformation, under a gravitational shear stress τg , the peak shear stress τp decreases to a residual τr after a characteristic distance δ. The propagation condition for a linear-elastic slab overlying a slip-weakening layer is (Reference McClungMcClung, 1979, Reference McClung1981):

where E is the average elastic (or viscoelastic modulus) of a slab of thickness H. Laboratory-scale experiments by Reference McClungMcClung (1977) indicated δ | 2 mm, and τr/τp | 0.75, although others have reported values for τr /τp as low as 0.1 (Reference De Montmollide Montmollin, 1982; Reference Perla, Beck and ChengPerla and others, 1982). Model assumptions require L to be larger than the end-zone, where the distribution of stresses through the slab is not linear. Physically, this length is expected to be several slab thicknesses. Following from case 1, immediate crack propagation is expected if τg exceeds τp.

Fig. 2. Schematic of a snow slab overlying a weak layer that contains a flaw (where the gravitational shear stress τg is not fully supported) of length 2L. The lower plot shows a weak layer with a peak shear strength τp, that slip-weakens to a residual strength τr.
The mechanical properties of snow depend strongly on microstructure (Reference KryKry, 1975), but the relevant microstructural properties are not generally known nor measured. Although not ideal, bulk density is more easily (and more often) measured and offers a practical alternative. Both snow strength and ductility increase rapidly with density and experiments show a power-law relationship explains much of the variability in measurements of shear strength (Reference Perla, Beck and ChengPerla and others, 1982; Reference JamiesonJamieson, 1995):
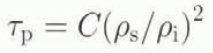
where τp is the peak shear strength (in Pa), ρ s is the snow density and ρi is the density of ice (917 kg m−3). The coefficient C depends on grain structure and varies from 1.8 × 104 Pa for open-grain structures (such as faceted grains) to 2.2 × 104 Pa for partly metamorphosed new snow.
For dry low-density snow (< 400 kg m−3), the elastic modulus E (in Pa) is also conveniently described by a power-law relationship (Reference Gibson and AshbyGibson and Ashby, 1987; Mellor, 1977):

The average modulus for a layered slab can be approximated as:

where E 1, E 2, etc. are the values of the modulus of layers of thickness H 1, H 2, etc.
Numerical Examples
Equation (1) implies sub-critical crack growth will occur only when the flaw or imperfection exceeds a certain length. For practical purposes, it is of interest to determine the minimum flaw size needed to initiate slow-failure propagation. The size depends on the mechanical properties of the system and it is convenient to study the length as a function of τp /τg because rearrangement of Equation (1) shows this relationship is relatively insensitive to changes in slope angle, slab thickness and density of both the slab and the weak layer. I restricted the analysis to flaws with a half-length less than 10 m, because rapid dynamic failure was expected if the “flaw” extended over a large area.
Values for the mechanical properties were estimated using Equations (2) and (3) for a range of conditions typically observed at avalanche-fracture lines (e.g. Reference McClung and SchaererMcClung and Schacrer, 1993). The gravitational shear stress τg was assumed constant and failure initiated from a flaw (of half length L), where the basal shear strength τr was less than τg. For simplicity, I assumed the residual strength of the basal layer (after shear-strain softening) was also τr and used the slip-weakening model (Equation (1)) to examine the sensitivity of L to changes in properties of the slab and the weak layer.
Results, together with values used for model input, are shown in Figure 3. τp/τg has been called “the stability index” by several authors; failure is expected to be immediate (i.e. L = 0) when the stability index is 1.0. The model discrepancy (shown in Figure 3 when τp/τg = 1) arises because of end-zone effects discussed earlier. Nevertheless, results show clearly that the length of the flaw needed to cause sub-critical crack growth decreases rapidly as τp/τg decreases. Indeed, the length decreases by about 50% when τp/τg decreases by only 10%. Changes of this magnitude could arise if either the slope angle, slab density, slab thickness or weak-layer density changed by just 5–10%, which is well within the bounds of natural variability measured across slopes. This sensitivity contributes to making accurate field assessment of slope stability problematic.
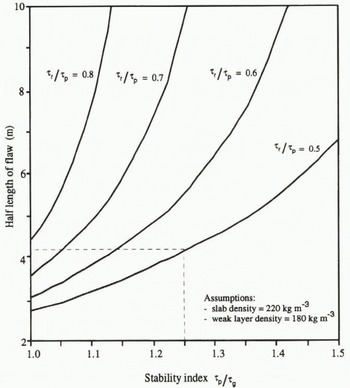
Fig. 3. Half-length of flaw needed to cause sub-critical crack growth as a function of the stability index τp/τp and the strain-softening ratio τr/τp. Results show sub-critical crack growth can initiate from relatively small flaws well before the average stability index decreases to 1.0. The example shows (for τp/τg, = 1.25) a flaw of half-length 4.2 m will propagate when τr/τp = 0.5 but the half-length necessary for propagation increases (unrealistically) to more than 400 m when τr/τp = 0.8.
Results shown in Figure 3 also indicate the flaw length is highly sensitive to the residual strength. Reducing the residual strength allows initiation of sub-critical crack growth from relatively small flaws well before the average stability index for the slope becomes unity. Figure 3 shows (for τp/τg = 1.25) a flaw with a half length of just 4.2m will result in sub-critical crack growth when τr/τp = 0.5, but the length increases rapidly to more than 400 m when τr/τp = 0.8. (Such a long length is unrealistic, because the zone is no longer a “flaw”.) The idea that widespread slope failure can initiate from a relatively small flaw is supported by measurements which show the average stability index for avalanched slopes is usually greater than 1.0 (Reference JamiesonJamieson, 1985).
Uncertainties in the spatial and temporal distribution of snow properties and flaws make it difficult to predict snow-slope stability accurately. However, the abrupt change in stability at the onset of rain offers some clues about conditions in the snowpack prior to rain and this is considered in the next section.
Avalanching at the Onset of Rain
Observations suggest that new snow often exists in a mela-stable condition and small perturbations at the onset of rain cause abrupt and widespread avalanching. Reference McClungMcClung (1996) showed that the elastic modulus is highly temperature sensitive and experimental evidence indicates it is often reduced by an order of magnitude with the introduction of liquid water. The elastic energy released by the slab following an abrupt decrease in the slab modulus would would be available to drive crack propagation (Equation (1)). Assuming the modulus prior to rain E0 is constant through the slab of thickness H0 , using Equation (4) the average modulus after rain E 1 can be written:

where E s is the modulus of the wetted surface layer of thickness Hs . Generally, E s H s ≪ E 0 (H0 - H s) and a reasonable approximation for the slab-averaged modulus is:

Here, H 0 - H s can be considered to be the “effective” slab thickness after welling. Assuming τp, τr and δ do not change in the first few minutes following the onset of rain but allowing that additional loading from rain may increase the basal shear stress to τg1 , re-arrangement of Equation (1) yields

Measurements of creep and temperature discussed above indicate that liquid water and the associated alteration of the mechanical properties are usually limited to the upper 0.1–0.15 m during the first 15 minutes of rain. Typical rates of precipitation in the region (5-10 mm h−1) would increase the gravitational shear stress by about 30–60 Pa h−1 on a slope of angle 38°. Figure 4 has been constructed to show the length of flaw needed to cause sub-critical crack propagation before and after rain (using Hs = 0.12 m and Δτg = 10 Pa to simulate conditions 15 minutes after rain starts). The separate effects of the additional loading and alterations to the slab modulus are shown. The plot is truncated at small values of Δp/Δg (before rain), because the extra loading from rain increases sufficiently so that Δg = Δp and immediate failure is expected. Forcases where the stability index is higher, rain-induced alterations reduce the length of flaw needed to initiate sub-critical crack growth by 10–20%. Such changes (|2 m or less) are small but the abrupt increase in avalanche activity soon after the onset of rain implies the changes are sufficient to initiate sub-critical crack propagation and ultimately rapid dynamic failure.

Fig. 4. Half-length of flaw needed to cause sub-critical crack growth as a function of the stability index Δp/Δg before and after rain. The intermediate dashed curve shows the impact when only the elastic modulus in the upper 0.12 m of the slab is reduced. The envelope between the solid curves gives the range of possible basal conditions before rain. For example (for Δp/Δg = 1.25), a flaw of half-length smaller than 5.6 m could have existed without expanding before rain but it must have been larger than 4.6 m for the slope to fail immediately after rain started.
The analysis supports observations that freshly deposited snow is often unstable. For example, for conditions given in Figure 4 and Δp/Δg = 1.25, the model predicts that before rain the slope must have contained a flaw of half-length between 4.6 and 5.6 m, because rain-induced alterations would not be sufficient to initiate sub-critical crack propagation from a smaller flaw, and propagation would have begun before rain started if the flaw were larger. This rather narrow band of pre-failure conditions is more likely to exist in freshly deposited snow, because sintering processes usually act to increase the strength of snow with time. Our observations indicate that abrupt and widespread avalanche activity is rare when rain falls on older, well-bonded snow packs.
Model results may also yield insight into skier-released avalanches. A ski-cut about 0.1 m deep would reduce the “effective” slab thickness at least locally and have a similar impact to that shown in Figure 4 (even without accounting for all the additional stress imposed by the skier). Observations indicate that rain is a more effective trigger of new snow avalanches than ski-cutting (personal communication from C. Wilbour, 1996). The difference may be that rain-induced alterations occur over a wide region and perturb all existing imperfections in the snowpack. A skier might miss culling across a flawed zone.
Conclusions
Measurements of snow properties and stratigraphic observations at slab-avalanche fracture lines provide the basis for adapting a slip-weakening model in which slip at the bed is non-uniform and the basal shear strength degrades to a residual strength with ongoing slip. Non-uniform slip implies the existence of crack-like flaws or imperfections in the basal layer, where stresses from the overburden are not fully supported. As the flaw-size increases, stress concentrations at lhe edges will cause sub-critical crack growth and subsequent rapid-failure propagation. Using values typical for properties measured at avalanche fraclure-line profiles, the model predicts sub-critical crack growth can initiate from a relatively small flaw, well before the gravitational shear stress approaches the peak basal shear strength. This result is consistent with field observations and measurements at avalanche-fracture lines.
Measurements indicate that alterations induced by rain on new snow are usually restricted to the upper 0.15 m of the snowpack. The slip-weakening model predicts such surface alterations will reduce the length of flaw needed to initiate sub-critical crack growth by just 15–20%. Apparently, this relatively small perturbation is sufficient to cause the abrupt change in stability often observed at the onset of rain. Conditions prior to rain must have been close to critical, which is consistent with field observations that indicate freshly deposited snow is often very unstable.
The slip-weakening model shows that the slab modulus can have a controlling influence on slope stability; it is evident that both the slab and the weak layer act together to control slope stability. Most field practioners focus on the basal layer, when searching for a stability index, but it may also be useful to examine the properties of the slab for clues about snow-slope stability.
Acknowledgements
This research was funded by the U.S. Army Research Office (grant No. DAAH04-95-1-0172) and their support is gratefully acknowledged. I also wish to thank R. Benedict, S. Breyfogle, R. Gibson, H. -P. Marshall, L. A. Rasmussen, L. Reddon and C. Wilbour for assistance. Comments by J. Johnson, D. McClung and C. F. Raymond greatly improved an earlier version of this manuscript.






