GRAIN GROWTH IN POLAR ICE
The size of crystals in snow and ice in polar regions, as measured by the mean grain area on thin sections, increases with depth of burial. The growth rate of crystals has been measured at several locations in Antarctica and Greenland (Gow 1975; Gow and Williamson 1976; Narita and Maeno 1979- Duval and Lorius 1980; Alley and others 1982; Herron and Langway 1982).
At Byrd Station, grain growth seems to stop at 450 m depth. At Camp Century, results suggest that grain growth stops at 400 m depth. At Vostok and Dome C where the mean annual surface temperature is respectively -56 and -54’C, grain growth is observed at least down to 900 m. However, a rapid decrease in grain size appears to be associated with the climatic Holocene-Wisconsin transition. In all cases grains remain equal-sized.
The time dependence of the growth rate of ice crystals is analogous to that observed in metallic and ceramic materials in that grain area (l2) increases linearly with time t:
The driving force for grain growth has been given by Hillert (1965). The driving force F is positive for a grain size l larger than the average grain size T and negative otherwise, ie
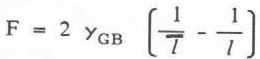
where yGB is the grain boundary energy (≈ 0.065 J/m2) The growth rate K is expressed by:
where T is the temperature, R is the gas constant and Q is the activation energy of the growth process. Figure 1 shows the variation of K with temperature in snow and in ice. The apparent activation energy obtained from the straight line (regression line) is 52 kJ/mole, which is slightly higher than the value given by Gow (1969) for snow (48.6 kJ/mole). Equation 1 is observed to describe grain growth only if the drag force from pores is not significant. Examination of thin sections of firn reveals that pores remain on grain boundaries during grain growth. This means that pores must migrate along with boundaries. Since the crystal growth rate takes the same value in firn and in ice, the restraint on boundary movement by pores does not appear to be important This can only be the case if pore mobility is much greater than boundary mobility.

Fig. 1. Temperature dependence of crystal growth rate in polar ice.
Below the firn-ice transition, bubbles show no tendency to migrate to grain boundaries during grain growth (Gow 1968a). Separation of pores from the boundary occurs when the drag force due to pores which is proportional to the pore size and the number of pores per unit grain boundary area, is small compared with the driving force for grain growth. For Byrd Station, the mean diameter of air bubbles is about 0.95 mm at the pore close-off depth whereas the crystal size is about 2 mm (Gow 1968a). Since, at this depth there are as many crystals as bubbles (Gow 1968a), the drag force of pores is weak.
DEFORMATION MECHANISMS OF POLAR ICE AT SHALLOW DEPTH
In the first hundred meters of polar ice caps deviatone stresses are smaller than 0.1 MPa and strain rates lower than 10-11s-1, From the deformation map given by Duval and others (1983) the expected detormation mechanisms are diffusional creep and power law creep. At Byrd Station, the compressive vertical strain rate is about 2.5 x 10-12s2-1 (Whillans and Johnsen 1983), which gives a deviatoric stress δ’zz = 0 088 MPa for diffusional creep and δz = 0.053 MPa for power law creep (Duval and Lliboutry, 1985). Dislocation creep would therefore be the dominant flow mechanism for the Byrd ice cores from the surface. But Duval and Lliboutry (1985) assumed that the continuous boundary migration was a much more efficient process for the accomodation of grain boundary sliding than the diffusional flow. On the other hand. Equation 1 implies that strain energy is small in comparison with the grain boundary energy which drives grain growth. The stored energy for dislocation creep increases with strain and can be higher than 104 J/m3 after a strain of 1% (Duval and others 1983). Since the driving force F (Equation 2) is typically of order 100 J/m3, power law creep is not compatible with grain growth.
Analysis of the inclinometer survey of the Byrd borehole by Lliboutry and Duval (1985) shows that the Newtonian viscosity of the ice is three to four orders of magnitude lower than theory of diffusional creep predicts. Results from Camp Century (Greenland) confirm those at Byrd Station (Paterson 1983). But, Paterson gives a value of flow parameter A of the power law creep (ε = AT n) for Holocene ice fifteen to twenty times greater than that expected from laboratory tests. A good fit of data from both stations is found with a flow model with n = 3.
As concerns the dislocation glide, grain growth should impede strain-hardening. The stored energy from dislocations near grain boundaries could be lower than that necessary to initiate recrystallization (= 104 J/m3) and than the driving force for grain growth (100 J/m3), If ρg is the density of dislocations near grain boundaries, ρg K./l2 dislocations per unit area and per unit time will be annihilated by grain boundary migration. In order for grain growth to occur, the accumulation of dislocations against boundaries must not exceed a critical value ρgc. A density ρ of dislocations has an associated energy of roughly:
where G is the shear modulus and b is the Burgers vector.
By assuming that E = 10 J/m3 we have a critical dislocation density of about 1010/m2.
In conclusion, grain boundary migration associated with grain growth in polar ice may be an efficient accomodation process for grain boundary sliding and for dislocation glide.
PRESSURE SINTERING OF POLAR ICE
Stages of snow densification
The densification of polar snow is generally divided into three stages. In the first stage (density ρ<0.55g cm-3), densification is dominated by grain packing. Mechanisms such as evaporation-condensation contribute to sintering in the presence of temperature gradients (Gow 1975). Rapid grain growth in the top 10 m of snow must also be taken into account. This stage is not analysed in this paper.
During the second stage (ρ< ρc the pore close-off density) densification is determined by the ice deformation near the contact regions of grains.
In the final stage the increase in the ice density beyond p is attributed to bubble compression, and densification is determined by the creep of ice surrounding bubbles. By analysing several physical properties of firn such as the air permeability, Maeno and others (1978) have proposed a critical density of 0.73 g cm-3. At this density air bubbles are concentrated at intersections of grain boundaries and the further densification results in the splitting of air channels (Narita and others 1978).
Mechanisms of densification
Several physical mechanisms may operate during the densification process: particle rearrangement, diffusion, and dislocation creep. The sintering of firn is driven by capillary forces and specially by the pressure due to the overburden snow. Figure 2 gives the relationship between the snow density and the snow load pressure at Byrd Station. At the pore close-off the snow load pressure is 0.419 MPa compared with deviatone stresses for the flow of ice sheets lower than 0.1 MPa (Gow 1968a). In the second stage the effective pressure acting on a particle contact is higher than the load pressure (Arzt and others 1983). Therefore, the expected dominant mechanism of densification should be power law creep. The complete treatment of the power law creep model was given by Wilkinson and Ashby (1975). The laws for densification relate the densification rate p to the load pressure and to the value of the density p. In the final stage, pores are considered as spherical holes and densification is determined by the creep of ice surrounding each pore. In the intermediate stage (ρc > ρ>0.55 g cm3) pores are considered as a network of cylindrical holes.

Fig. 2. Density and snow load pressure versus depth at Byrd Station (80°0I’S, 119°32’W; mean annual temperature -28 °C; accumulation rate: 15,7 g cm-2 year-1), ρc is the pore close-off density. Data are from Gow (1968b).
The rate of densification is expressed by:

for cylindrical pores, and

for spherical pores, where P is the load pressure, Pi is the bubble pressure, A and n are constants of the power law creep, and ρi is the density of bubble free ice.
Figure 3 shows the variations of the rate of densification and of the effective pressure with density at Byrd Station. Density data are after Gow (1968b). The effective pressure was calculated with the pore close-off density ρc = 0.825 g cm-3 and ρi = 0.9204 g cm-3 as suggested by Gow (1968a). The rate of densification decreases by a factor higher than 3 within the intermediate stage in spite of the important increase in the effective pressure. But, as suggested by Equations 5 and 6, ρ/ρ decreases with density for a constant effective pressure.

Fig. 3. Densification data for ice at Byrd Station. A) Densification rate versus density B) Effective pressure versus density.
The densification rate can be corrected for the effect of density by dividing by f(p), where

The adjusted ρ/ ρ/f(ρ) versus the effective pressure curves are plotted in Figure 4 (see Table 1) with n = 3.
The rate of densification increases with stress, but the power law creep model does not seem verified.
DISCUSSION
Results given in Figure 4 show that the densifjcation models constructed by Wilkinson and Ashby (1975) cannot be applied to polar snow just as they are As shown by Maeno (1982) and by Arzt and others (1983), diffusional creep is not an efficient mechanism ol densification for the intermediate stage and for the major portion of the final stage. Several factors which have not been taken into account can influence the densification rate (Maeno and Ebinuma 1983). The most important is probably grain growth. Since the crystal
Table 1. EXPERIMENTAL DATA FOR POLAR ICE AT BYRD STATION.

growth rate takes the same value in firn and in bubble free ice, the strain energy resulting from the deformation near grain boundaries by the effective pressure must belower than the driving force for grain growth, This is possible only if grain boundary migration impedes strain hardening

Fig. 4. Densification rate normalized for the effect of porosity as a function of the effective pressure at Byrd Station. Power law creep model was applied with n = 3.
In conclusion, dislocation creep is probably the densification mechanism for polar ice; but constants A and n in the power law creep cannot be derived from the minimum creep rate obtained after a deformation of about 1%.







