Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T05:21:09.446Z Has data issue: false hasContentIssue false
  • English
  • Français

Grain Coarsening of Snow Particles Immersed in Water and Solutions

Published online by Cambridge University Press:  20 January 2017

Katutosi Tusima
Katutosi Tusima*
Affiliation:
Toyama University, Faculty of Science, 3190 Gofuku, Toyama, Japan 930
Rights & Permissions [Opens in a new window]

Abstract

In order to clarify the metamorphic process of snow particles immersed in water, distributions of grain size were examined as functions of time (0.1 to 1 000 hrs) and impurity concentrations. When disaggregated snow particles were immersed in water kept at 0°C, each particle became spherical and grain coarsening took place with time. The average diameter increased with cube root of time and the average volume increased in proportion to time. Grain coarsening was not detected in a kerosene environment.

In solutions of glucose, NaCl, HC1 and dextran, the growth rate was controlled by the concentration and the diffusivity of the solute. The higher concentration and the lower diffusivity, the grain coarsening was controlled. The grain coarsening is explained by the disappearance of relatively small particles and growth of relatively large ones, caused by differences of the equilibrium temperature of each particle if the total ice mass is conserved.

Type
Research Article
Information
Annals of Glaciology , Volume 6 , 1985 , pp. 126 - 129
Copyright
Copyright © International Glaciological Society 1985

INTRODUCTION

Melted water infiltrating into deposited snow may be stopped by a special layer of snow, causing the snow immediately above it to be saturated with water. It is well known that larger and more rounded granular snow is formed in such a saturated layer. This snow has a characteristic of weak bonds and low strength, and frequently causes wet avalanches. Snow fallen on pond or lake may be immersed in water for several months or more. In this case, very large ice spheres up to several mm in diameter can develop (Fuzioka and others 1963).

Wakahama (1965, 1968, 1974) studied the metamorphism of snow saturated with water by the analysis of many thin sections. Colbeck (1974, 1976, 1980) considered grain growth of wet snow theoretically. Tusima (1978) studied the grain coarsening of snow particles saturated experimentally with pure water. Tusima and Raymond (1979) extended the study to impure water. Raymond and Tusima (1979) analyzed the grain coarsening as the process of growth and disappearance of grains caused by heat flow from relatively large grains to relatively small grains.

An immersed ice sphere of 1 mm diameter has a depression of the equilibrium temperature near 10-4°C because of surface curvature. We deal with growth under the ultra small supercooling.

METHODS OF EXPERIMENT

Figure 1 shows the apparatus schematically. The outer and inner stainless containers contain crushed ice and wet snow, respectively. The outer (0.8 m in diameter, 0.8 m long) has a drain pipe in the bottom. Polymethytmetacrylate containers are filled with 350 ml of deionized water or solutions of d-glucose, NaCl, HCl and dextran ((C6H1005)n, molecular weight 5 x 105) were held one day at 0 C. Next, fresh or compact snow was mixed in with a glass rod. For some solutions greater than 0.1 mol/1, large vacuum flasks ( 4 1 and 6 1) were used. From these containers, a small amount of snow (0.5 ml) was scooped out at various times and spread in a single layer in shallow dishes and pressed down with a glass plate. This snow was photographed under a microscope. The sizes of particles were measured with a KG-2 analyzer. Usually, 500 particles were analyzed. Experiments were carried out in a cold room precisely controlled to 0.6°C.

Fig. 1. Experimental apparatus (used for pure and dilute solutions).

RESULTS

Size distribution

Figure 2 shows photographs of snow at times of 1, 5, 10, 50 and 130 hrs after saturation with pure water. As time passed, the distribution range became wider and the average diameter shifted to larger size. Similar curves were obtained for solutions except for the position were located to smaller side depending on concentration.

Mean grain size

When the average diameter, ? (mm), was plotted against the cube root of time, a linear relation was obtained as shown in Figure 4:

(1)

where t is the time (hr), and α and ß are constants. For pure water, the values of α and ß are 0.16 and 0.08, and for glucose (0.1 mol/1) are 0.15 and 0.07, respectively. The relation of ? to time is also shown in Figure 5.

Average volume

The plot of average volume, v (mm5), to time, t (hr), gave a linear relation as shown in Figure 6:

(2)

Coefficient ρ is equal to the volume growth rate and the value is listed in Table 1. The average volume is given by the ratio of number of particles, N, to total ice volume, VQ, Suppose the total ice mass was conserved, the growth rate of volume is given by:

(3)

Fig. 2. Photograph of snow particles: 1) initial snow particles (before immersion in water) 2) after 1 hr 3) 10 hr, 4) 100 hr, 5) 1000 hr, 6) 5000 hr. Note scale change for 6.

Fig. 3. Size distribution of particles for pure water.

Fig. 4. Relation between average diameter of snow particles and cube root of time.

The increase of v means the decrease of ice particles, N. It is seen N decreased in proportion to time, except for smaller range than 10 hrs (Figure 7). 56 particles at 1 hr decreased to 19 after 5 hr, 12 after 10 hr and 1.6 after 100 hr per unit ice mass, 1 mg.

Grain coarsening in kerosene

In order to prohibit mass transfer through liquid, and estimate the role of mass transfer through the ice bonds, snow was immersed in kerosene at 0°C. In this case, snow was not disaggregated. No grain coarsening was visible and the irregularities of snow particles were kept after 100 hrs (Figure 8) and 200 hrs.

Master curve of grain coarsening

Each curve in Figure 5 could be made to coincide with a -t curve of pure water by shifting in size and time (Figure 9). This suggests that the same mechanism controls the grain growth in the solutions and pure water.

DISCUSSION

Any snow particles have to be their equilibrium temperature at interface between particles and water or solution. In general, snow is an aggregation of ice particles and includes small particles as well as large ones. Therefore, it is considered that each particle is located in any temperature field. Equilibrium temperature for some particles will be higher than circumstance one and for others will be inverse. Former particles grow and later ones melt and disappear. The temperature field will change at every moment in the process of grain coarsening, which involves growth, disappearance, and decreasing numbers of grains.

Table 1. Comparison Of Growth Rate Of Average Volume For Experiment And Theory (For Glucose).

Fig. 5. Relation between average diameter and time. Left - glucose; middle - NaCl; right - HCl (o, ·); dextran (+) and broken line (pure water).

Fig. 6. Relation between average volume and time, glucose.

Consider the growth (or melting) of snow particle placed in the solution of concentration S. We suppose the solution is surrounded by an isothermal wall, at the molar depression temperature - ρS, Heat flow through any spherical surface, q, is given by:

(4)

where r is the radius of spherical surface, κ the thermal conductivity of the solution. The temperature T is:

(5)

where T° - 273 K, ρ l the density of ice, r the particle radius, L the latent heat of fusion, and σLS the interfacial tension. Because the growth rate of ice particles depends on inflow heat, Equation 4 becomes:

(6)

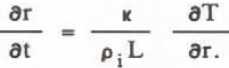
Fig. 7. Number of snow particles per unit ice mass (1 mg) against time.

Fig. 8. Photograph of snow particles immersed in kerosene (after 100 hr).

Fig. 9. Master curve for grain coarsening of glucose solution.

Fig. 10. Growth rate of radius against temperature (supercool): 1) this experiment, 2) James (1967), 3) and 4) Hilling (1958), 5) Hilling and Turnbull (1956).

Equation to diffusion of solute is written:

(7)

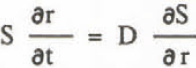
where D is the diffusion coefficient. From Equations 5, 6, and 7,

(8)

where B is the coefficient of r-2. The growth rate of volume is given by

(9)

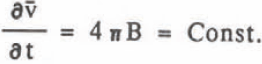
This agrees with the experimental result that the average volume growth rate was constant. The value B is equal to p in Equation 2 and the comparison of these values agree very well as seen in Table II. Integration of Equation 8 gives the relation diameter 0 and time t, which corresponds to Equation 1,

(10)

From Equations 5 and 6, we can get the following relation to growth rate and temperature,

(11)

From Equations I and 5, we get an experimental relation,

(12)

These agreements are very good. Figure 10 shows Equation 12 in comparison with the growth rates of James (l967), Hilling and Turnbull (1956), and Turnbull (1958) (or see Fletcher: 114-115). The tendency of curve is reasonable. It is necessary to notice some particles grow and others melt or disappear in the process of coarsening. Therefore, Equation 12 is not a strict relationship, but may give some information on the growth rate with slight supercooling.

Table 2. Growth Rate Of Average Volume.

CONCLUSIONS

Grain coarsening of snow particles immersed in pure and impure water are measured. Remarkable grain coarsening was observed. The average diameter increased with cube root of time and average volume increased with time. The higher concentration and the lower diffusion of solute controlled the growth rate. No grain coarsening observed in kerosene. Grain coarsening is considered as the process of the growth of relatively large particles and disappear relatively small particles which caused by temperature difference between each particles.

References

Colbeck, S C 1974 Grain and bond growth in wet snow. International Association of Hydrological Sciences Publication 114 (Symposium of Grindelwald 1974 – Snow Mechanics): 51-61 Google Scholar
Colbeck, S C 1976 Thermodynamic deformation of wet snow. CCREL Report; 7-44 Google Scholar
Colbeck, S C 1980 Thermodynamics of wet snow metamorphism due to variations in curvature. Journal of Glaciology 26(94): 291-301 CrossRefGoogle Scholar
Fletcher, N H 1970 The chemical physics of ice. Cambridge, Cambridge University Press Google Scholar
Hilling, W B 1958 The kinetics of freezing of ice in the direction perpendicular to the basal plane. In Doremus, R H Roberts, S W, Turnbull, D (eds) Growth and perfection of crystals: 350-360 Google Scholar
Huzioka, T, Tabata, T, Kinosita, S 1963 [Snow jam in Lake Oze]. Low Temperature Science A 21: 95-115 Google Scholar
James, D W 1967 Solidification kinetic of ice determined by the thermal-wave technique. In Peiser, H S (ed) Crystal growth; 767-773 Google Scholar
Raymond, C F, Tusima, K 1979 Grain coarsening of water-saturated snow. Journal of Glaciology 22(86): 83—105 CrossRefGoogle Scholar
Tusima, K 1978 [Grain coarsening of ice particles immersed in pure water]. Journal of the Japanese Society of Snow and Ice 40(4): 155-156 Google Scholar
Tusima, K, Raymond, C F 1979 [Grain coarsening of snow saturated with solution]. Journal of the Japanese Society of Snow and Ice 41(2): 91-99 Google Scholar
Wakahama, G 1965 [Metamorphism of wet snow]. Low Temperature Science A 23: 51-66 Google Scholar
Wakahama, G 1968 The metamorphism of wet snow. International Association of Hydrological Sciences Publication 79: 370-379 Google Scholar
Wakahama, G 1974 The role of melt water in densification process of snow and firn. International Association of Hydrological Sciences Publication 114 (Symposium of Grindelwald 1974 - Snow mechanics): 66-72 Google Scholar
Figure 0

Fig. 1. Experimental apparatus (used for pure and dilute solutions).

Figure 1

Fig. 2. Photograph of snow particles: 1) initial snow particles (before immersion in water) 2) after 1 hr 3) 10 hr, 4) 100 hr, 5) 1000 hr, 6) 5000 hr. Note scale change for 6.

Figure 2

Fig. 3. Size distribution of particles for pure water.

Figure 3

Fig. 4. Relation between average diameter of snow particles and cube root of time.

Figure 4

Table 1. Comparison Of Growth Rate Of Average Volume For Experiment And Theory (For Glucose).

Figure 5

Fig. 5. Relation between average diameter and time. Left - glucose; middle - NaCl; right - HCl (o, ·); dextran (+) and broken line (pure water).

Figure 6

Fig. 6. Relation between average volume and time, glucose.

Figure 7

Fig. 7. Number of snow particles per unit ice mass (1 mg) against time.

Figure 8

Fig. 8. Photograph of snow particles immersed in kerosene (after 100 hr).

Figure 9

Fig. 9. Master curve for grain coarsening of glucose solution.

Figure 10

Fig. 10. Growth rate of radius against temperature (supercool): 1) this experiment, 2) James (1967), 3) and 4) Hilling (1958), 5) Hilling and Turnbull (1956).

Figure 11

Table 2. Growth Rate Of Average Volume.