1. Introduction
Mapping ice-surface elevation with continent-wide coverage is presently best achieved by satellite radar altimetry. Since Seasat in 1978, several satellite missions with radar altimetry have taken place. Since 1991, the European Remote-sensing Satellites ERS-1 and -2 have provided radar altimeter (RA) data that can be used for monitoring changes in Antarctic and Arctic ice mass balance by time series of elevation models built with RA data of subsequent observations. Monitoring of ice mass balance is important for assessing sea-level changes, and accurate elevation models serve as data sources for numerical models of ice movement. The satellite missions differ in scientific goals, as well as in schedules of repeat time and coverage. RA data have a semi-rhombic ground-track pattern with gaps of several kilometers between tracks, depending on latitude and observation method. Thus, interpolation of RA data is required to determine an elevation model of the Antarctic ice sheet. Interpolation is best performed using methods from geostatistics, the theory of regionalized variables (Reference MatheronMatheron, 1963; Reference Herzfeld, Lingle and LeeHerzfeld and others, 1993; Reference HerzfeldHerzfeld, 2004). There are high-resolution elevation models from stereo images of synthetic aperture radar (SAR) data using interferometric analysis, but until now only regional elevation models exist from SAR. During the 1997 RADARSAT-1 Antarctic Imaging Campaign, SAR data covering the entire continent were collected. We utilize these data in the form of a 125m pixel backscatter mosaic compiled by Reference JezekJezek (1999) to improve mapping from RA data for the Lambert Glacier/Amery Ice Shelf system.
However, SAR data are not elevation data, but backscatter data, hence elevation may only be inferred indirectly. Here, we take a different approach in that SAR data are used only as an aid in delineating different regions according to their morphological characteristics. Subsequently a complex geostatistical method known as kriging within strata (KWS) (Reference GoovaertsGoovaerts, 1997) or stratified kriging is applied to interpolating elevation values from RA data in each of those regions. KWS refers to mapping within geological units in a sedimentary-geology setting. In our situation, the units in which different kriging interpolators are applied are morphological units of the Lambert Glacier/Amery Ice Shelf system. The interpolators are specific to regional morphology in the variograms that determine the interpolation kernel; the type of interpolator is still ordinary kriging. The resultant digital elevation models (DEMs) are presented and compared.
2. Data Acquisition
The nominal area of interest is 63–75˚ S, 59–79˚ E. The RA data of the map area are transformed by Universal Transverse Mercator (UTM) projection, resulting in an orthogonal coordinate system which is essential for kriging. The map area extends from 7578 to 8322 km UTM South and 215 to 785 km UTM East related to the central meridian at 69˚ E (zone 42). To get enough RA data for interpolation and to ensure nearly the same time interval as the SAR data, RA data from the period 1 August–31 October 1997 are used. The exact repeat observation method employed during this time causes gaps of 15–25km between parallel ground-track orbits each with several parallel repeat tracks separated by only a few to a hundred meters. There are missing data due to tracking errors, especially at the transition from the ice shelf to the surrounding ranges.
The RA data were processed by the Ice Sheet Altimetry Group at NASA Goddard Space Flight Center, Greenbelt, MD, USA (Reference Zwally, Bindschadler, Brenner, Martin and ThomasZwally and others, 1983), using the method for retracking by Reference Martin, Zwally, Brenner and BindschadlerMartin and others (1983), slope correction as described by Reference Brenner, Bindschadler, Thomas and ZwallyBrenner and others (1983), Goddard Earth Model (GEM) T2 orbits (Reference Martin, Zwally, Brenner and BindschadlerMartin and others, 1983) for data reduction, corrections for atmospheric effects and solid Earth tides as described by Reference Zwally, Bindschadler, Brenner, Martin and ThomasZwally and others (1983), and water-vapor corrections. The elevation is given with reference to the World Geodetic System 1984 ellipsoid (WGS84).
The first Antarctic Imaging Campaign of RADARSAT-1 lasted from 9 September to 20 October 1997. During this period, RADARSAT operated in a left-looking mode so that the entire continent could be mapped. During the first Antarctic Mapping Mission (AMM-1) a seamless digital SAR mosaic with 125m resolution was created at Byrd Polar Research Center, Columbus, OH, USA. The data provided are grey values of radar backscatter intensity deduced from 25 m resolution swaths used for the mosaic (Reference JezekJezek, 1999; Reference JezekJezek and RAMP Product Team, 2002). From these data a subset of Lambert Glacier/Amery Ice Shelf covering the same area as the RA data is extracted, georeferenced and converted to UTM.
3. Geostatistical Methods for Elevation Mapping
Interpolation of corrected and collocated RA data is carried out using geostatistical methods known as ‘kriging’. Kriging comprises a family of interpolation/extrapolation methods based on the least-squares optimization principle (Reference MatheronMatheron, 1963; Reference Journel and HuijbregtsJournel and Huijbregts, 1978). Kriging consists of two steps: (1) analysis of spatial structures (variography); and (2) estimation (kriging). The variogram analysis may be carried out (a) for the whole map area, using all data (a technique not applied here for computational and glaciological reasons), (b) using data from a representative subarea for mapping the whole area (used in the construction of the first DEM), and (c) varying regionally for units in the map area (used in the KWS method). The estimation step is performed for each grid node, based on data collected in its neighborhood and on the appropriate variogram model.
3.1. Structure analysis: variography
First an experimental variogram is calculated according to
where z(xi), z(xi + h) are measurements at locations xi , xi + h, respectively, inside a region D, and n is the number of pairs separated by the vector h. The experimental variograms are calculated from measurements and grouped in distance classes. A variogram model describes the type of transition from the strong covariation between closely neighboring samples to weaker covariation of samples farther apart. The variogram model is characterized by its function type, which has to meet the positive-definiteness criterion to ensure existence and uniqueness of the solution of the kriging system. The model is defined by three parameters: nugget effect (C0), total sill (C0 + C1) and range (a). The nugget effect is the residual variance of resampling in the same location and it also contains contributions caused by surface morphological features below the resolution of the altimeter footprint (called the support). The total sill is close to the total variance of the data. The concept of a regionalized variable perceives that closely neighboring measurements have a higher covariance than measurements spaced farther apart. For distances increasing from the support to the range, the variogram increases and the regionalization effect decreases; for distances beyond the range, the regionalized variable behaves like a random variable (probabilistically), and data with a distance larger than or equal to the range all have the same influence on the interpolated value (numerically).
3.2. Ordinary kriging
For the kriging method the value z0 = z(x0) at a position x0 is estimated by
with data zi = z(xi) at locations xi (i = 1, . . . ,n) in a neighborhood of the position x0 and weights αi . To obtain an unbiased estimate, the following condition is required:
This method is called ordinary kriging.
For simplicity, we use only one global Gaussian variogram model, with the following parameters: C0 = 25m2, C1 = 18m2, a = 16 000 m. The variogram was fitted to ERS-1 RA data from 1995 from around the grounding zone of Lambert Glacier (Reference Herzfeld, Stosius and SchneiderHerzfeld and others, 2000). It was fitted for the grounding zone of Lambert Glacier because this part is of essential interest for mass-balance studies. In this part of the glacier, the estimation error is low (Reference Herzfeld, Lingle and LeeHerzfeld and others, 1993). We choose this model to insure that the same interpolator is used for the ERS-1 and ERS-2 elevation models, and hence that the new elevation model presented in this paper may be compared to published elevation models of the Lambert Glacier/Amery Ice Shelf system (Reference Herzfeld, Mayer, Higginson and MatassaHerzfeld and others, 1996, Reference Herzfeld1997, Reference Herzfeld, Stosius and Schneider2000; Reference HerzfeldHerzfeld, 1999; Reference Herzfeld and MatassaHerzfeld and Matassa, 1999). Figure 1 shows the contour plot of elevations using ordinary kriging for estimation of a 3 km grid.
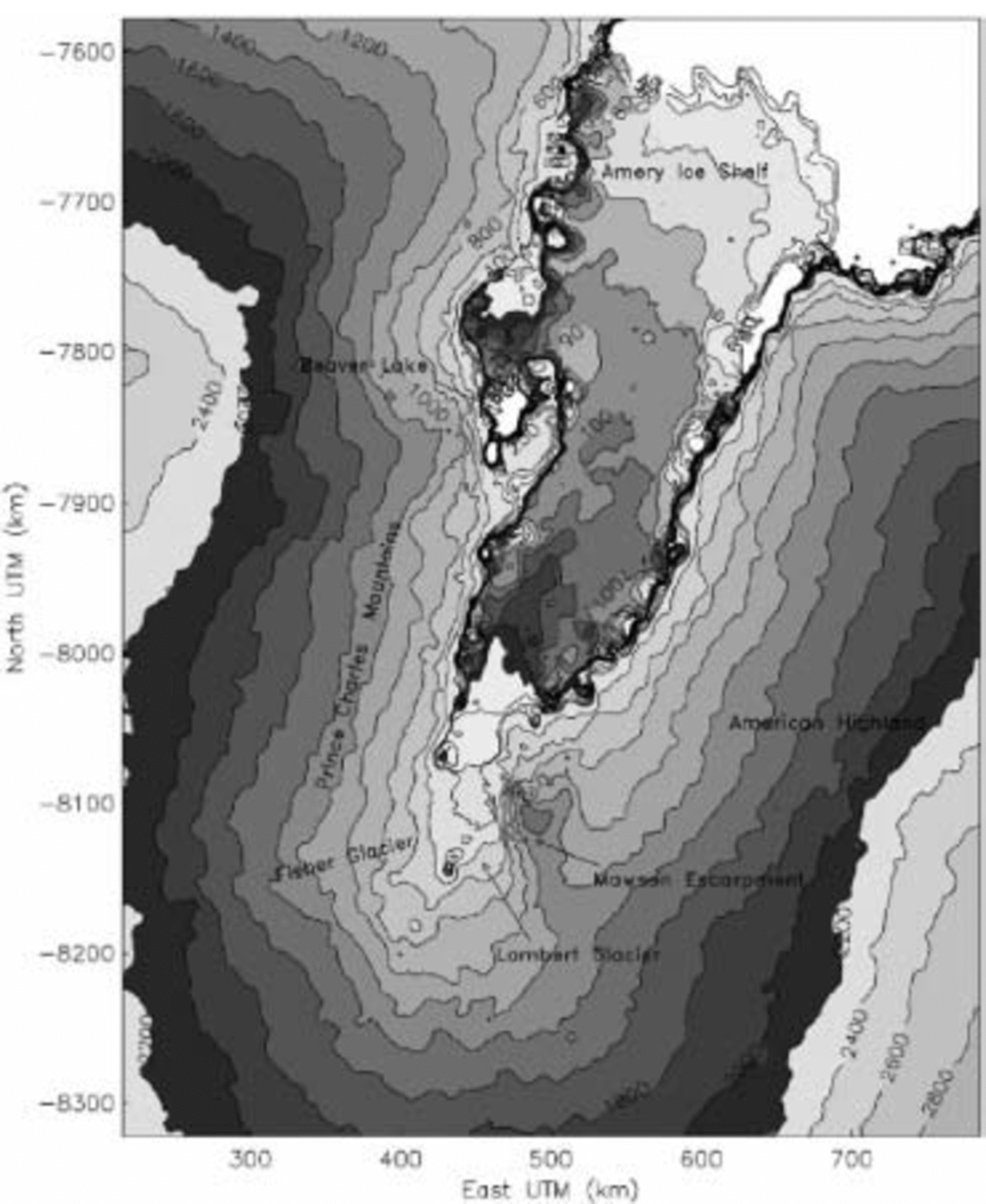
Fig. 1. Contour plot of a DEM with 3 km grid spacing deduced from 1997 ERS-2 RA elevations from the Lambert Glacier/Amery Ice Shelf system using ordinary kriging with a Gaussian variogram (C0 = 25 m2 ; C 1 = 18m2 ; range = 16 000m). Coordinates in km with respect to central meridian at 69˚ E, UTM zone 42. Elevations in meters with respect to WGS84 ellipsoid, 40–140m with 10 m contour lines, 140–200m with 20 m contour lines and 200–2800m with 200m contour lines.
3.3. Kriging within strata
Because the entire area of interest contains many morphologically different regions, ranging from at this scale rather smooth inland ice to rugged mountainous terrain, more than one variogram will be needed to capture the spatial variability of each region adequately. Therefore the Lambert Glacier/Amery Ice Shelf study area is subdivided into apparently homogeneous morphological regions. For this segmentation, visually detectable features in the SAR mosaic are used to define the borders between morphological regions. The assignment of an RA datum to a region is performed by a point-in-polygon algorithm. In every region a small area (Fig. 2) of up to 75 km2 is extracted for fast variogram calculation.
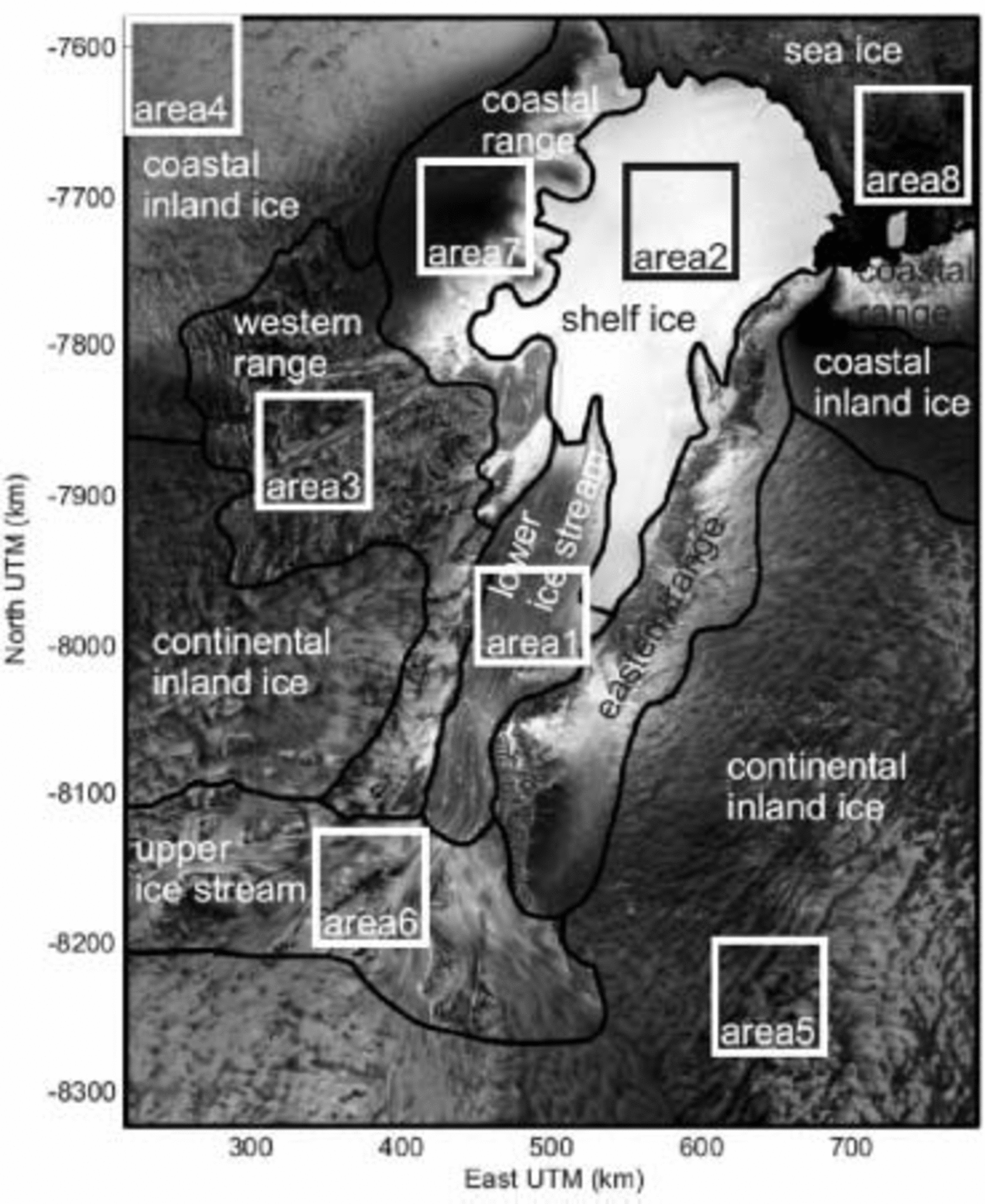
Fig. 2. Regions and areas used for KWS deduced from the RADARSAT-1 SAR mosaic (Reference JezekJezek, 1999) of the Lambert Glacier/Amery Ice Shelf system.
The influence of the semi-rhombic data distribution with ascending and descending track directions is very strong. The number of data pairs with distance h equal to the distance between parallel track orbits increases dramatically and causes peaks in the experimental variogram. Therefore only directional variograms in the direction of the ascending and descending ground tracks are used. To take into account the semi-rhombic structure of the data distribution, a quadrant search with eight sectors is performed. The variogram models fitted to these variograms are supposed to have the same nugget and sill. If the ranges of the variograms from the two directions differ, the spatial structure is anisotropic.
The spatial structure of areas 1–6 is fitted best by two nested Gaussian variogram models with nugget effect, which is
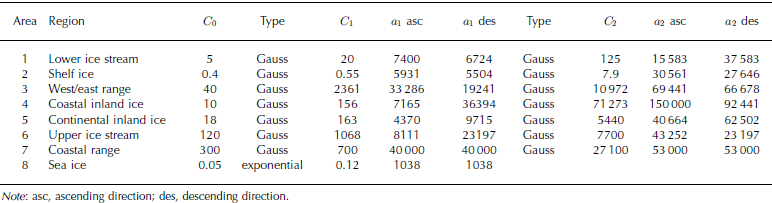
where C0 is the nugget effect, C1 and a1 are the sill and range parameter for the first and C2 and a2 are the parameters for the second spatial structure. In area 7 the anisotropy is too complex to fit adequate directional variogram models, so we use only a global nested Gaussian model. Area 8 is the sea-ice region which is fitted by a global exponential model. The fitting is performed using SFIT, an automatic fitting program of Reference Jian, Olea and YuJian and others (1996). SFIT uses the Levenberg–Marquardt method, which is one of the best for parameter estimation of non-linear functional models. For every region the characteristic variograms are calculated for a lag increment of 300 m which is the mean distance between subsequent measurements along track after collocation. The areas and their corresponding vario- gram models are listed in Table 1.
Table 1. Areas and corresponding nested variogram model parameters. Range parameters (a) in m, sill parameters (C) in m2
In every region the estimation of elevation is executed separately by ordinary kriging using GSLIB (Geostatistical Software Library, Stanford University) routines from Reference Deutsch and JournelDeutsch and Journel (1998). Anisotropies are incorporated by assigning variograms derived for descending tracks to 45˚ and variograms derived for ascending tracks to 135˚. Then the regions are combined again into one DEM and map (Fig. 3). This method of subdivision and recombination is known from geological applications as KWS (Reference GoovaertsGoovaerts, 1997) or stratified kriging.
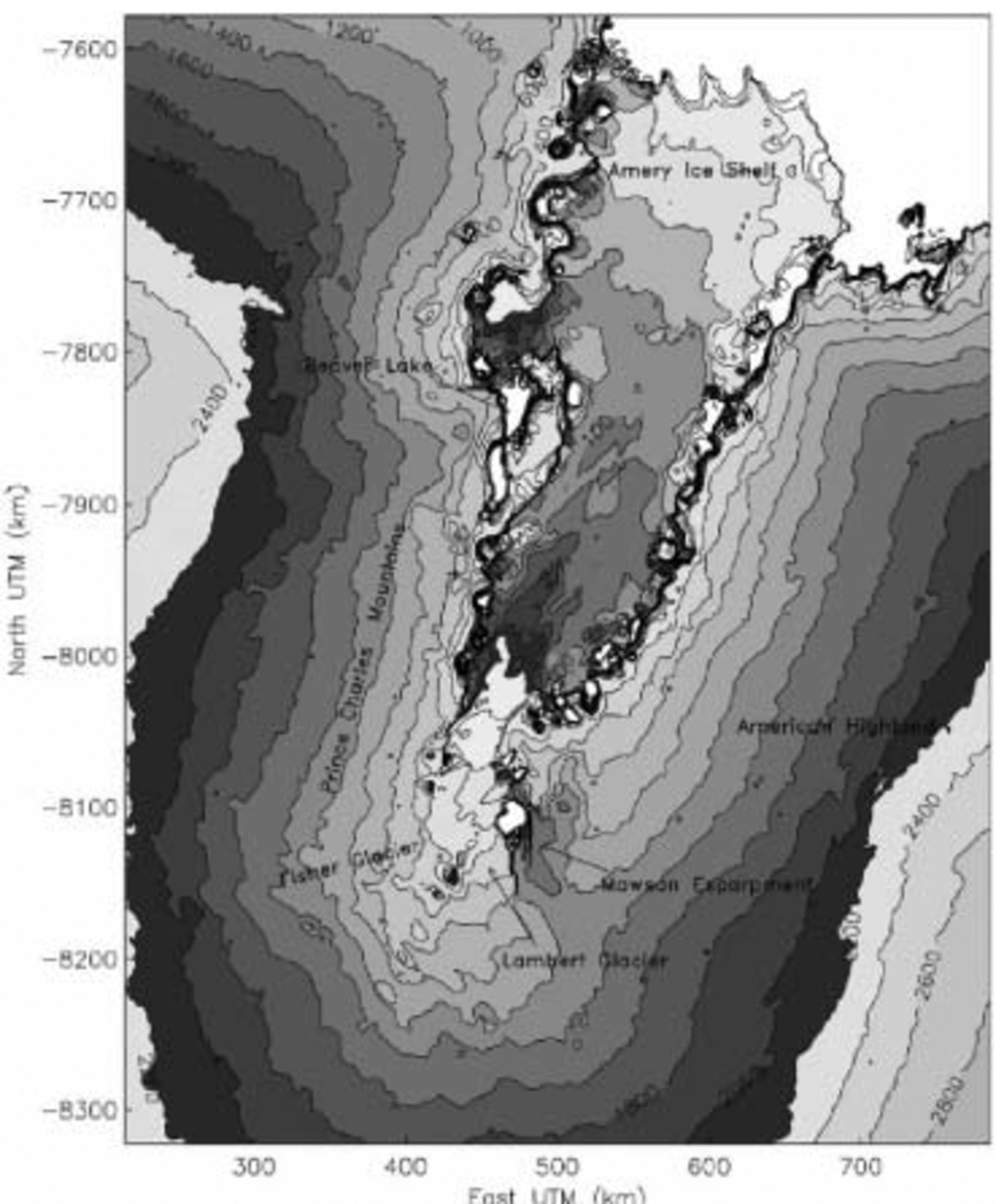
Fig. 3. Same as Figure 1 but using KWS (ordinary kriging with locally variable variograms) instead of ordinary kriging.
4. Comparison of Different Kriging Methods and Resultant Dems: Discussion and Conclusions
4.1 Cross-validation
To compare the two methodologies applied in this paper, we perform cross-validation (Reference Deutsch and JournelDeutsch and Journel, 1998).
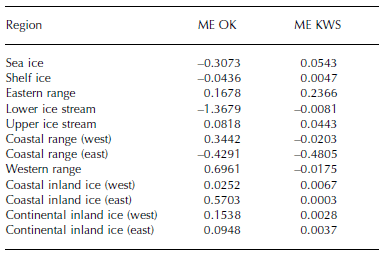
For each region the mean error (ME) between the true values z(xi) and the estimated values z*(xi) at every RA measure- ment position xi is calculated for ordinary kriging and KWS respectively. The absolute mean errors for KWS are lower than for ordinary kriging within most of the regions (Table 2). Only within the eastern range and the eastern coastal range do the absolute mean errors become higher. This may be because no specific variograms are calculated within these regions but they were erroneously assumed to be described by the same variogram as the western range and the western coastal range. The calculated errors show the mean deviation of the estimated values from the known measure- ment values in meters. Cross-validation provides only an indicator of the quality of the estimation, but not a numerical error value of the DEM.
Table 2. Cross-validation mean errors (ME) for ordinary kriging (OK) and kriging within strata (KWS) for each region in meters
4.2. Surface morphology
The contour lines of the map in Figure 1 are generally smoother than those of the map in Figure 3. The variogram model used for kriging the map in Figure 1 has a high nugget-effect-to-sill ratio, which is necessary (1) to counter- act the effect of the ground-track pattern on the experimental variogram and (2) to model the smooth surface of the glacier adequately (for a definition of the nugget-effect ratio, see Reference Herzfeld, Stosius and SchneiderHerzfeld and others, 2000). The surface morphology of all other units is hence neglected, and KWS provides a methodto remedy this situation. Other authors (e.g. Reference Fricker, Hyland, Coleman and YoungFricker and others, 2000) limit the area of DEM calculation to the main Lambert Glacier and Amery Ice Shelf for glaciological reasons and thus avoid the problem of matching different morphological types. Purely mathematical interpolation algorithms are not capable of morphological modeling and consequently are only useful for one unit (e.g. low-slope interior of Antarctica in Reference BamberBamber (1994)). Reference Fricker, Hyland, Coleman and YoungFricker and others (2000) utilize ordinary kriging, but take an automated, least-squares approach to variogram modeling and fit ascendingand descending tracks separately, which may have led tooverfitting. An expression of this is too rough and noisycontours on the glacier and ice-shelf surfaces (parameters are not published).
The salient problem is to distinguish mathematically between altimeter-signal properties and errors, on the onehand, and geophysical or morphological properties of the surface, on the other hand, and hence between variogram modeling and variogram fitting. The surface of the ice-stream/ice-shelf system is best represented in the map inFigure 1. The morphological complexity of the large Lambert Glacier/Amery Ice Shelf region led to selection of eightdifferent units, which necessitated spatial information from non-RA data; a solution was facilitated by SAR data. In variogram modeling for each unit, a semi-automated approach was applied to distinguish specific properties. As a side effect, altimeter errors that appear in the experimental variograms are also modeled. When kriging with more complex variograms of different regions and considering anisotropies, the different morphological features of the regions become more prominent, in particular those of the rougher environments, which is correct (map in Fig. 3). However, the close fitting of experimental variograms that is the result of automated fitting of variogram models has the effect that track-pattern-induced artefacts and other errors may also be picked up in combination with morphological properties, as is visible in central areas of the glacier and iceshelf (Fig. 3). We conclude that KWS is advantageous in thatvariograms specific to the local morphology may be used if variograms can be modeled adequately. The possibilities of modeling are also limited by the altimeter data quality.
Where RA data are missing due to tracking errors, estimation errors occur in both maps, especially at the transition between the ice shelf and the surrounding ranges. Some of these estimation errors in the map in Figure 3 maybe intensified due to a border effect, i.e. too few data nearthe borders of a region. To overcome this problem, a fuzzier definition of the borders, such as border zones instead of border lines between regions, may be useful.
5. Summary
We have utilized a synopsis of ERS-2 RA data with RADARSAT-1 SAR data for calculation of DEMs of Lambert Glacier/Amery Ice Shelf, using two different kriging algorithms. Ordinary kriging with a modeling approach to variography proved best for mapping the ice-stream/ice-shelf system itself, at the same time reducing altimetry artefacts. Kriging within strata is an advanced kriging method that facilitates mapping of large areas with morphologically different geographical regions, as demonstrated for the Lambert Glacier/Amery Ice Shelf region and its surroundings. Morphological units were delineated using co-referenced SAR data. The KWS method involved calculation of variograms, fitting anisotropic variogram functions and application of ordinary kriging as the interpolation algorithm for all data within each morphological province. Resultant maps exhibit the different morphological characteristics of each geographical region, but also follow altimeter errors more closely. Cross-validation values are lower for KWS than for ordinary kriging for a large part of the mapped area, which is, albeit not a numerical error quantity, an indication of the quality of the map.
Last but not least, accuracy of a DEM and its morphological quality are limited by the survey instrumentation, and more precise mapping of surface structures may be expected from a combination of advanced geomathematical methods and data from advanced altimeters such as RA-2 (Envisat), GLAS (ICESat) and CryoSat instruments.
Acknowledgement
The authors thank T. H. Jacka for comments on the manuscript.







