INTRODUCTION
Snow scientists have been interested in the possibility of thermal convection in snow for a variety of reasons. Trabant and Benson (1972) have suggested that thermal convection explains the high mass flux rates they observe in a subarctic snowcover. However, no direct observation of thermal convection has ever been made.
If convection occurs with flow perpendicular to the slope (perpendicular to the isotherms), the rate of heat and water vapor transport will be greatly increased. Such flows occur when convection appears in a multicellular form termed Benard convection. Benard convection occurs only when the ratio of buoyancy to viscous forces is sufficiently high. The calculation of the critical conditions for the onset of convection for a saturated porous medium is discussed by Palm and Tveitereid (1979). Powers and others (1985) give a more sophisticated treatment covering the more complex problem of convection in a snow layer.
Experimental observations of thermal convection in a saturated compact of glass beads and in snow are reported here. Our observations establish that thermal convection can occur in snow under conditions common to sub-arctic regions, and possibly in more temperate snowcovers as well. Although it is clear that heat and mass flows are significantly increased by thermal convection, it is not clear what affects convection will have on snow metamorphism. However, the observation of thermal convection in a snowcover is itself significant since it ends two generations of unquantified speculation about that possibility.
THEORY OF CONVECTION IN POROUS MEDIA
The basis for the present work is the theory which has been developed to describe thermal convection in any porous medium. Fairly complete reviews of this theory are given by Combarnous and Bories (1975) and Cheng (1978). That general work was extended to describe the more complex problem of convection in a snow layer by Powers and others (1985); part of that work is reviewed here.
Convection occurs when buoyant forces are sufficient to overcome viscous drag. The ratio of buoyant to viscous forces is given by the Rayleigh number

where ρ o is the density of the fluid at some reference temperature, β the coefficient of thermal expansion of the fluid (˚C-1), μf the fluid viscosity (kg/m-s), g the acceleration of gravity, AT a charcteristic temperature difference, H the layer depth and K the intrinsic permeability (m2). The parameter it is a thermal diffusivity defined as km /(pCp) f where (pCp ) f is the volumetric heat capacity of the fluid and k a thermal conductivity of the porous media which includes both fluid and solid contributions.
In a horizontal layer heated from below and cooled from above, convection occurs when the Rayleigh number exceeds a critical value. This critical value depends on the boundary conditions and on lateral confinement. The influence of lateral confinement is important only if both internal dimensions are much less than the layer depth H, and is not considered here. The influence of upper and lower boundary conditions are tabulated in Table 1, and are very significant. In Table 1 we consider an upper boundary which is impermeable and either an isothermal or uniform heat flux boundary. The four combinations given in Table I are those which we feel cover the range of interest in the study of convection in a snow layer. While the boundaries are almost never completely impermeable, the lower boundary is almost always relatively impermeable compared to the snow cover.
Table I. CRITICAL RAYLEIGH NUMBER FOR SEVERAL COMBINATIONS OF BOUNDARY CONDITIONS. AFTER NEILD (1967).

iso — constant temperature boundary flux - uniform heat flux boundary imp - impermeable boundary perm - permeable (constant pressure) boundary
Fluid begins to flow when the Rayleigh number exceeds the critical value. Flow occurs in cellular patterns which may be either hexagonal cells or two-dimensional rolls (Combarnous and Bories 1975). The rate of heat transfer as increased by the flow is described by an effective thermal conductivity, k eff which is defined as the ratio of the heat flux to the temperature gradient, both of which must be averaged horizontally due to the cellular nature of the convection. Results are commonly presented in dimensionless form by the Nusselt number, defined as
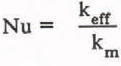
For heat transfer between isothermal and impermeable boundaries, the Nusselt number is well described by

for Rayleigh numbers greater than the critical value (Elder 1967). This correlation describes both numerical and experimental results well (Powers and others 1985). The Nusselt number equals one for Rayleigh numbers less than the critical value.
We have not treated the problem of multi-layered snow covers because the wide variety of possible conditions makes it difficult to draw specific conclusions. If layering is present, it can affect the conditions necessary for the onset of convection as well as the strength of the convection should it occur. There has been a lot of work done on the effects of layering on convection in porous media and much of this work can be applied directly to snow.
EXPERIMENTS
The theory discussed above provides guidance for experiments to detect the presence of convection in snow. By heating the bottom and cooling the top, and measuring the heat flux and temperature profiles, we can plot an effective thermal conductivity, keff as a function of heat flux or temperature difference across the sample. If keff increases with increasing temperature gradient, then convection is contributing to heat transfer.
Prior to doing experiments on snow we conducted experiments on glass beads, using either water or air as the saturating fluids. These experiments were performed as a test of the experimental procedure. Results for convection studies with similar glass beads are well known (Bau 1980).
The apparatus for glass bead experiments is shown in Figure 1. Cold air was blown over an aluminum plate at the upper boundary. The lower boundary was heated using electric heating pads. Because these pads dissipated heat uniformly and at a constant rate, the heat flux was assumed to be constant over the lower boundary. This was desirable because the uniform flux condition is a realistic lower boundary condition for convective flows in snow. However, all previous experiments on convection in porous media have held the bottom boundary at a constant temperature.
A sketch of the experimental apparatus for snow is shown in Figure 2, The top is kept isothermal by circulating glycol from a constant temperature bath through a cold plate. Variations in temperature were less than ± 0.1 °C along this boundary. The bottom was heated using an electric heating pad, as in the glass bead experiments.

Fig. 1. Apparatus for glass bead experiments.

Fig. 2. Side view of apparatus for snow experiments.
The snow sample had lateral dimensions of 0.4 m x 0.1 m and was 0.5 m high. These dimensions were chosen to force a two-dimensional form of convection in the experiments. The two-dimensional form is easier to analyze both experimentally and theoretically, and neither the onset of nor the heat transfer by convection is different from the three-dimensional form. To minimize heat losses through the large sides, similar snow samples were kept on either side of the test sample. Heat losses were a greater problem in experiments with snow because of the low thermal conductivity. These exterior samples were heated and cooled in a manner similar to the interior sample; thus the temperature gradients across the wall between them were kept to a minimum, reducing heat losses. Each heater was controlled independently so that the best match of temperature profiles could be made. On the narrow ends, where heat losses were less of a problem because of the smaller area for heat flow, a loose styrofoam insulation was placed outside the polystyrene wall. This loose insulation was also heated and cooled to reduce heat losses. While the match between the temperature profiles was not as good on the ends, losses through the ends were smaller because of the reduced area.
The net heat flux through the sample was calculated from the heat input plus or minus any gains or losses through the sidewall. Heat flows through the sidewalls were calculated using the temperature difference across the midpoint of each wall. All temperatures were measured with the thermocouples along both vertical and horizontal axes. An average temperature gradient was then calculated using the vertical temperature profile at the centerline of the sample. The effective thermal conductivity was then calculated as the ratio of the net heat flux to the average gradient.
The snow was disaggregated and dropped into the apparatus. A snow density of about 250 Mg/m3 and grain size of about 1.5 mm was achieved. One snow sample was used for all of the experiments so we were concerned about grain growth and density changes. However, no settlement of the snow was observed, and at the conclusion of the tests no appreciable grain growth had occurred. The lack of grain growth was partly attributed to crystal poisoning by the refrigerant, trichloroethelene. To check on changes in the physical properties during the tests, the temperature gradient was first increased from the lowest to the highest values and then decreased to repeat the tests at low temperature gradients. Since no change in k eff was found at a low temperature gradient, we concluded that no significant changes in the physical properties had occurred.
RESULTS AND DISCUSSION
Results are presented in Figures 3, 4 and 5, where keff is shown as a function of the net heat flux. Net heat flux is chosen as the independent variable, rather than the temperature difference from top to bottom, because at the bottom boundary a flux is specified rather than a temperature. The error bars shown are based on uncertainty in the value of the heat flux through the sides and the bottom. We had information about the gradients through the walls only at the midpoints, thus our calculations of the fluxes through the sides and the bottom were approximate. How good our approximations were is not known, thus we took the error in the measured keff to be the percentage of the net heat flux due to side fluxes which probably overestimates the error. Uncertainties in temperature measurements and in calculation of the heat input were considered negligible. Our method probably overestimates the uncertainty.

Fig. 3. Effective thermal conductivity versus net heat flow through glass bead with air. Calculated keff is shown.

Fig. 4. Effective thermal conductivity versus net heat flow through glass beads with water. Calculated keff is shown both with and without thermal convection.

Fig. 5. Effective thermal conductivity versus net heat flow through snow. The errors bars are an upper limit based on estimated heat flow out the sides; the actual errors are probably much less.
Figures 3 and 4 show the results from the experiments with glass beads, with air and water as the saturating fluid, respectively. Theoretical predictions are given for comparison. The theoretical value of thermal conductivity in the absence of convection (horizontal lines) is calculated from the model of Luikov and others (1968). The Luikov model correctly predicted the observed thermal conductivity in the experiments of Bau (1980), who used the same glass beads as in the present work, with water as the saturating fluid. The data from our experiments also agree well with the Luikov model.
The point at which convection is expected to begin is calculated from the theory presented earlier. When the bottom boundary is a uniform heat flux, q, the characteristic temperature difference is given by
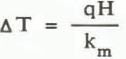
The critical heat flux for the onset of convection is then given by

The physical properties of the porous medium appear as k m, K and H. The thermal conductivity can be calculated from the Luikov model, or estimated from the experimental data. The layer height is known. The permeability, K, is calculated from the Carmen-Kozeny relation (Wallis 1960).

where d is an average particle diameter and € the porosity. Bau (1980) measured permeabilities of glass beads and found that the Carmen-Kozeny relation described the permeability well.
The calculated critical heat fluxes for the glass bead experiments with air and water are 2.60 x 10 3 W/m 2 and 54.5 W/m 2, respectively. From Figure 3 we see that the value for the experiments with air is outside the experimental range; thus we expect and observe a constant conductivity with increasing heat flux. In the experiments with water the critical heat flux is well within the experimental range. The break in the theoretical curve of Figure 4 occurs at the heat flux value calculated above, and indicates the theoretical onset of thermal convection.
Above the critical heat flux, we expect the effective thermal conductivity to increase as convection intensifies. The numerical computations of Powers, Colbeck and O’Neill (in press) indicate that the heat transfer rate for a layer with a constant flux lower boundary condition is best represented by

so long as the remaining physical properties in the Rayleigh number are constant. This relation gives the slope of the line to the right of the critical heat flux value in Figure 4. Again, the agreement is good between experiments and theory.

Fig. 6. Effective thermal conductivity versus net heat flow through snow. The sloped line is calculated from theory. The horizontal line is from the measured thermal conductivity below the critical Rayleigh number.
Figure 6 shows the results of experiments with snow, presented without error bars for clarity, in comparison with theoretical results. For snow the values of thermal conductivity and permeability are not well known. Thus we cannot predict a priori the critical heat flux for the onset of convection, nor can we predict the thermal conductivity, k m. The value of k eff on the horizontal part of the curve in Figure 6, and the point indicating the onset of convection on this curve are both based solely on the experimental data. The slope of the line beyond the critical heat flux is calculated from Equation 7. From Figure 6 we see that the experimental results behave in a manner consistent with our theoretical understanding, although an exact comparison of theory and experiment cannot be made because of uncertainty in the value of the permeability.
It is possible to estimate the permeability from the experiments if all the other physical parameters in the Rayleigh number are known. The only other unknown in the present experiments is the thermal conductivity, k m. In the experiments we measure an effective thermal conductivity, which includes heat conduction, vapor diffusion, and convection. In the absence of convection (q < q cr ) the average value of k eff from the experiments is 0.24 W/m. K. This k eff is related to k m by

where Deff is the effective diffusion coefficient, LE the latent heat of sublimation, and ∂ρv/∂T the change in vapor density at saturation with temperature. Yosida (1955) measured Deff and found an average value of 8.5 x 10-5 m2/s, invariant with snow density. Evaluating ∂ρv/∂T at the average sample temperature of -12 C, we calculate a value of km equal to 0.20 W/m-k). Although there is much uncertainty as to the value of Deff, the vapor diffusion contribution to heat transfer is, fortunately, much smaller than the heat conduction contribution, and thus the uncertainty in km due to uncertainty in Deff, is not large.
Using values for properties of air evaluated at -10°C, and a qcr equal to 7.8 W/m 2 from the experiments, we calculate an intrinsic permeability of 9.4 x 10-8 m2. This is higher than most reported permeabilities. Our snow sample was comprised of coarse-grained snow, with a density of 250 kg/m and an average grain size of 1.5 mm. Data on permeabilities of coarse-grained snow in this density range are somewhat scarce. Bader (1939) measures permeabilities as high as 2.5 x 10-8 m2 for coarse-grained snow and depth hoar in the density range of the current experiments. Johnson (personal communication) has measured permeabilities of about 5 x 10-8 m2 in depth hoar layers of interior Alaska. The snow density of his experiments were less than 200 kg/m3 and thus his permeabilities would be likely to be greater than those in the present experiments. From the above information, it seems unlikely that our permeability is as high as our experiments would lead us to believe. Thus our experiments raise the possibility that we may have observed convection at lower Rayleigh numbers than we would expect from theory. We have no explanation for the discrepancy between theory and experiment, other than uncertainty in permeability.
CONVECTION AND SNOW METAMORPHISM
When convection does occur, it must be accounted for in our description of vapor transport in snow and the metamorphism of snow. Because convection is cellular, the convective transport can be in the same direction as, opposite to, or perpendicular to the diffusion of vapor. Thus the effects of convection on snow metamorphism will vary spatially in a snow cover. In the absence of convection, water vapor transport occurs entirely by diffusion. The bottom of a snow cover is usually warmer than the top, and thus the vapor density is highest at the bottom. Vapor diffuses upwards. The dominant mechanism of vapor diffusion is what Yosida (1955) called “hand-to-hand” transport, that is, vapor diffuses directly from warm particles to adjacent cold particles. Thus the rate at which a cold particle grows is equal to the rate of mass transfer from the warmed particle. This mechanism allows significant grain growth to occur without a net accumulation of vapor. Thus grain growth increases as the flux rate increases, and not as the accumulation rate increases. Where flow is in the same direction as diffusion, we expect the vapor transport rate, and thus the rate of snow metamorphism, to increase substantially. Flow opposite the diffusive flux should retard metamorphism. It is not well understood what effect the flow perpendicular to the temperature gradient will have.
Quantifying the effects of convection on snow metamorphism is more difficult. If, as we implied earlier, the growth rate at a snow particle is proportional to the flux rate of vapor to the particle, then by comparing diffusive and convective flow rates we should learn something about the relative influences of diffusion and convection on snow metamorphism. The easiest fluxes to compare are the macroscopic fluxes. The parameter a, defined as

gives the ratio of the convective flux to the diffusive flux, each averaged over a sufficient number of particles. The Darcian velocity is equal to the volumetric flux rate of the saturating fluid, in this case air. The ratio ρv∂ρv/∂T is relatively independent of temperature, and is “equal to 11.2 K. For a temperature gradient of 40 K/m, a calculated (Powers and others 1985) air velocity of 4.0 x 10-4m/s and an effective diffusivity of 8.5 x 10-5 m2/s, a is slightly more than one. We suspect that since both the convective and diffusive fluxes are averaged over an area of many particle sizes, the a calculated in this manner is also an average, and that a will be distributed such that local values may be either greater or less than the average value. The implication of this calculation is that convection will be just as important as diffusion in determining the rate of snow metamorphism for these particular conditions.
The above analysis seems most applicable to the case of flow in the same direction as the diffusive flux. In this case, the convective flux will transport warm, moist air to a cold particle, and thus the tendency will be for the vapor to condense. When flow is opposite the diffusive flux, the convection is transporting cold, dry air to a warm particle. This air will always be undersaturated with respect to the downwind particle, and thus even if the connective vapor flux is greater in magnitude than the diffusive flux, the downwind particle will not grow in the direction of the oncoming convective flux. In this case, it would seem that the convection would tend to erode the windward side of particles, while the diffusion will continue to deposit vapor on the lee side.
It appears obvious that a full analysis of the effects of convection on snow metamorphism is beyond the scope of both this paper and our current research efforts. An additional complication is that, according to the flow regime criteria established by Donaghey (1980), the flow on a local scale must be considered mixed convection, implying that to describe the local flow field one must first fully describe the local temperature field. Thus even on the local scale a complex set of coupled differential equations must be solved before the mass transport problem can even be considered. This will indeed by a formidable task, but hopefully also one which will be fruitful, both to those working in snow metamorphism and to the crystal growth community as a whole.
The solution of the mass transfer problem should enable a fuller description of the snow metamorphism process, given recent advances in our understanding of the interfacial kinetics of ice particles (Colbeck 1983; Kuroda 1983). It is worth noting the work of Keller and Hallet (1982) who observed a change in crystal habit with increasing ventilation rates, even in the absence of a -significant change in the growth rate. Although they simulated conditions more typical of atmosphere than of a seasonal snow-cover, the trends they observe may well apply to the case of present interest. Of special importance is their observation that ice crystals became more skeletal and fragile (depth hoar like?) when a flow was imposed on the environment.
CONCLUSIONS
The experimental results show that thermal convection can occur in snow. The comparison with theoretical analysis indicates that convection occurs more readily than theory predicts; however, there is much uncertainty about this conclusion because of our uncertainties about the permeability of snow. The experimental results with glass beads compare very favorably with the theoretical results, and thus it appears that it is only because of the special problems encountered in dealing with snow that the experiments were not more precisely revealing. While it is clear that convection, when it does occur, significantly transfers both heat and water vapor, it is not entirely clear what effect those fluxes will have on snow metamorphism. Although it now appears that thermal convection does occur in snow, much remains to be done to fully understand its effects.









