Introduction
Studies on glacier mass balance are regarded as important in connection with sea-level rise, water resources and other concerns related to climatic change (e.g. Reference Dyurgerov and MeierDyurgerov and Meier, 1997; Reference Liu, Kang, Liu, Chen and LiuLiu and others, 1999; Reference HoughtonHoughton and others, 2001). Mass-balance models are necessary to examine the response of glaciers to climate change and to understand spatial and temporal variations in mass balance. However, only a few numerical studies of mass balance based on physical energy-balance simulations at the glacier surface have been performed in the Himalaya and the Tibetan Plateau (e.g. Reference Kayastha, Ohata and AgetaKayastha and others, 1999; Reference Fujita and AgetaFujita and Ageta, 2000) due to the lack of high-quality meteorological data in these regions.
Temperature-index models are widely used for estimating mass balance when available data are limited. The most commonly used temperature-index model is the degree-day model, which predicts ablation as the product of the sum of all positive daily mean air temperatures in ˚C and the degree-day factor. The simplicity of the degree-day method has advantages. However, degree-day factors vary spatially and temporally (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000; Reference Kayastha, Ageta and NakawoKayastha and others, 2000, Reference Kayastha, Ageta, Nakawo, Fujita, Sakai and Matsuda2003; Reference HockHock, 2003) because they are affected by the complex process of surface energy balance contributed by temperature, solar radiation and other environmental conditions. Therefore, the degree-day factor must be essentially determined by means of field data of ablation and air temperature.
Since absorbed solar radiation is generally the dominant component of the surface energy balance over melting glaciers (e.g. Reference Ohata and HiguchiOhata and Higuchi, 1980; Reference Bamber and PayneBamber and Payne, 2004; Reference Sicart, Wagnon and RibsteinSicart and others, 2005), not only air temperature but also solar radiation must be a key factor even in the simplest mass-balance model (Reference OerlemansOerlemans, 2001). Therefore, not only physically based energy-balance models but also simple mass-balance models use solar radiation as input (e.g. Reference MartinecMartinec, 1989; Reference HockHock, 1999; Reference OerlemansOerlemans, 2001). Strong solar radiation in low-latitude regions also enhances its importance for estimating mass balance in the Himalaya and the Tibetan Plateau.
Re-analysis products, such as by the US National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR; Reference KalnayKalnay and others, 1996) and by the European Centre for Medium-Range Weather Forecasts (ECMWF; Reference Simmons and GibsonSimmons and Gibson, 2000), would be useful for estimating solar radiation and other meteorological variables needed as input for mass-balance models (e.g. Reference Reichert, Bengtsson and OerlemansReichert and others, 2001). Downscaling re-analysis data, however, is an inevitable step for small glaciers and ice caps due to the spatial resolution of re-analyses (e.g. 2.5˚ x 2.5˚ of NCEP/NCAR Re-analysis and ERA-40 by ECMWF). Moreover, data from several or more decades ago (e.g. before 1948 for NCEP/NCAR Re-analysis) are not available.
Atmospheric models such as general circulation models (GCMs) can simulate solar radiation and other climatic conditions and enable simulation of the response of the glacier mass balance to climate change (e.g. Reference GloverGlover, 1999; Reference Wild and OhmuraWild and Ohmura, 2000; Reference Reichert, Bengtsson and OerlemansReichert and others, 2001; Reference Casal, Kutzbach and ThompsonCasal and others, 2004). However, the computing costs of atmospheric models limit spatial resolution.
Since data on solar radiation are often unavailable, some previous studies derived solar radiation from other parameters. The dependence of solar radiation on cloud amount has often been examined (e.g. Reference Dobson and SmithDobson and Smith, 1989; Reference OerlemansOerlemans, 1993; Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1996; Reference Greuell, Knap and SmeetsGreuell and others, 1997). Reference Walter, Brooks, McCool, King, Molnau and BollWalter and others (2005) used the daily air-temperature range for estimating solar radiation. Though there are many meteorological stations in the Himalaya and the Tibetan Plateau (e.g. Reference Chalise, Shrestha, Thapa, Shrestha and BajracharyaChalise and others, 1996; Reference Liu and ChenLiu and Chen, 2000), the distribution density of meteorological stations is not uniform, and data on the cloud amount and daily air-temperature range are difficult to obtain in some areas. Moreover, meteorological station recordings do not provide information about pre-instrumental periods.
Analyses of ice cores and tree rings help to reveal past climatic information. Many analyses of ice cores (e.g. Reference Yao and ThompsonYao and Thompson, 1992; Reference Duan and YaoDuan and Yao, 2003; Reference Thompson, Mosley-Thompson, Davis, Lin, Henderson and MashiottaThompson and others, 2003) or tree rings (e.g. Reference Zhang, Cheng, Yao, Kang and HuangZhang and others, 2003; Reference Feng and HuFeng and Hu, 2005; Reference Singh and YadavSingh and Yadav, 2005) have focused on temperature and/or precipitation in the Himalaya and the Tibetan Plateau. Indeed, Reference Wang, Gong and ZhuWang and others (2001) reconstructed past temperature in China from ice-core and tree-ring data, and past accumulation rates estimated from non-melting ice cores can reveal past precipitation amounts. Other meteorological variables, however, are difficult to quantify reliably by analyses of ice cores or tree rings. If there were a method of estimating solar radiation from precipitation, it would be a useful tool at times when solar radiation cannot be obtained by other methods. Therefore we propose a new approach for deriving the solar radiation from precipitation.
Approach
Solar radiation on the terrestrial surface, S (Wm−2), can be expressed as:
where τ is atmospheric transmissivity of solar radiation, Tis topographic effects on transmissivity of solar radiation, and S0 is solar radiation at the top of the atmosphere (Wm−2). Since S0 can be calculated when the latitude of the location and time are given, solar radiation can be estimated if τ and Tare obtained.
The variable τ depends on atmospheric conditions such as cloud amount, cloud optical thickness, absorption by water vapor and other gases, and aerosol extinction. The term causing the largest uncertainty in the estimate of solar radiation is the cloud factor (Reference Bamber and PayneBamber and Payne, 2004). As precipitation is closely linked to clouds and is necessary for mass-balance calculations anyway, an examination of the relation between τ and precipitation can be meaningful, though it is obvious that precipitation amounts cannot represent instantaneous atmospheric conditions.
The variable T depends on many factors such as shading and reflections from surrounding slopes, and shading by surrounding mountains is generally the most important factor for the variation of S The variable S can be split into a direct part and a diffusive part. The magnitude of shading in the direct part and the diffusive part is different, and the ratio of the direct part to the diffusive part depends on the atmospheric conditions. Therefore, we calculated the average values of TS 0 with the assumption that T = 0 when the sun elevation is below the skyline of the surrounding mountains and T = 1 otherwise.
Data and Measurement Sites
We analyzed the dataset of precipitation and S measured at 11 sites in the Himalaya and the Tibetan Plateau. The locations of the measurement sites are shown in Figure 1 , and the measured monthly precipitation, monthly means of observed S and monthly mean air temperature used in this study are shown in Figure 2. The altitudes of these measurement sites range from 4279 to 5350 m. Precipitation during the monsoon season (May–September) is dominant, while during the non-monsoon season (October–April) little precipitation occurs in the Himalaya and the Tibetan Plateau (e.g. Reference Ding and KangDing and Kang, 1985; Reference Dai and DaiDai, 1990; Reference Chen, Huang and TakleChen and others, 2004). The fact that little surface-level increase is measured during the non-monsoon season at Xiao Dongkemadi glacier, which is near D105, (Reference Seko, Pu, Fujita, Ageta, Ohata and YaoSeko and others, 1994) and at July 1st (Qiyi) glacier (Matsuda and others, unpublished information) confirms that there is little precipitation during this period even in the mountain regions. The annual precipitation varies widely, from a few hundred mm on the northwestern Tibetan Plateau to >2000 mm on the south side of the Himalaya. The measurement periods of meteorological data used in this study are summarized in Table 1.

Fig. 1. Location map of study area. D, G, J, M, S and X denote D105,1,2 Gaize,3 July 1st glacier,4 MS3608,3 Shiquanhe,3,5,6 and D66,3 respectively. EN denotes the area including AX010 glacier,7 Yala glacier8 and Lirung glacier.8 BT denotes the area including Ganju La glacier9 and Lugge glacier.9 References are as follows: 1 Reference Ohta and AgetaOhta and Ageta (1996); 2 Reference Ueno and OhataUeno and Ohata (1996); 3GAME-Tibet (http://monsoon.t.u-tokyo.ac.jp/tibet/); 4 Reference Matsuda, Sakai, Fujita, Nakawo, Duan, Pu and YaoMatsuda and others (2004); 5 Reference Shiobara and AsanoShiobara and Asano (1992); 6 Reference Xu and HaginoyaXu and Haginoya (2001); 7 Reference Ageta, Ohata, Tanaka, Ikegami and HiguchiAgeta and others (1980); 8 Reference Fujita, Sakai and ChhetriFujita and others (1997); 9 Reference Ageta and KohshimaAgeta and Kohshima (2004).

Fig. 2. Measured monthly precipitation (bar), monthly mean solar radiation (dashed line) and monthly mean air temperature (solid line) at 11 measurement sites in Figure 1. Precipitation at D105 was adjusted to the value of the bush gauge.
Table 1. Measurement periods of precipitation and solar radiation. The monsoon season and the non-monsoon season run from May to September and from October to April, respectively

Meteorological data are point measurement values and do not reflect the mean distributed meteorological conditions. All meteorological measurements were taken at the same location, except for Yala glacier. Precipitation at Yala glacier was measured outside of the glacier (5110 ma.s.l.), while the other meteorological variables were measured on the glacier (5350 m a.s.l.), with a horizontal distance between two points of about 1 km. The measurement site at Lirung glacier was a debris-covered area on the glacier, while measurements at AX010, Ganju La and July 1st glaciers were made outside and near the terminus of the glaciers. The measurement site at Lugge glacier was a debris-covered area on the terminal dead ice. D105, D66, MS3608, Gaize and Shiquanhe stations were in open, flat fields. All measurement sites except those at Ganju La and Lugge glaciers were visited several times during the measurement period. Instruments at July 1st glacier were checked every few days during the summers of 2002–05, but were not checked during other seasons. Instruments at Ganju La and Lugge glaciers were checked once a year (autumn) due to the difficulties of reaching and staying at measurement sites.
Precipitation data were obtained manually at AX010 glacier by regularly measuring the accumulated precipitation in a tank, and automatically at other sites. Weighing rain gauges were used at D66 and MS3608. Unheated tipping-bucket rain gauges were used at the other sites, i.e. D105, Gaize, Shiquanhe, and Ganju La, July 1st, Lirung, Lugge and Yala glaciers. Tipping-bucket rain gauges cannot accurately measure precipitation falling as snow or when the bucket is frozen; and as reported previously, measurements of precipitation, particularly solid precipitation, are adversely affected by strong winds. Therefore, measured precipitation should be adjusted to the ‘true’ value of the bush gauge or Double Fence Intercomparison Reference (DFIR), which is a practical secondary standard (e.g. Reference Goodison, Louie and YangGoodison and others, 1998). Precipitation at D105 was adjusted to the value of the bush gauge (Reference Ueno and OhataUeno and Ohata, 1996). Since the catch ratios of gauges, which are the ratios of measured precipitation to DFIR value, at the other ten measurement sites are unknown, precipitation measured at these sites was not corrected. The potential impact of the measurement error on this study is discussed later.
The variable S was measured by pyranometers installed horizontally at all sites. The pyranometers used were EKO MS-800, EKO MS-801, EKO-MS601, Aanderaa solar radiation sensor 2770 and the Robitzsch pyranometer (manufacturer unknown). The Robitzsch pyranometer was used at AX010 glacier only, and Sat AX010 glacier was corrected by comparison with that simultaneously measured by the EKO MS-42 pyranometer. All solar radiation data were expected to be accurate to within ±5%.
The skylines of surrounding mountains were used for calculating daily and monthly means of TS0. The direction and elevation angle of skylines were surveyed at AX010, Ganju La, July 1st, Lirung and Yala glaciers by means of a transit compass. Digital elevation model (DEM) data of ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer) Level 3A01 product (http://www.science.aster.ersdac.or.jp/en/index.html) with 15 m spatial resolution were used for obtaining the skyline at Lugge glacier, and 3 arcsec DEM data by the Shuttle Radar Topography Mission (SRTM) (http://srtm.usgs.gov/, http://www2.jpl.nasa.gov/srtm/index.html) were used at D105, D66, Gaize, MS3608 and Shiquanhe.
Results and Discussion
Estimating atmospheric transmissivity of solar radiation
We calculated daily atmospheric transmissivity of solar radiation, Td, which is defined as the ratio of daily mean observed S to daily mean of TS0. The T d and daily precipitation, pd (mm), are shown in Figure 3. The T d converges toward about 0.2 with the increase of pd. The range of T d is, however, very wide when pd is small. Indeed, days without precipitation occur not only during clear weather conditions but also under overcast conditions. Therefore it is difficult to derive rd from pd.

Fig. 3. Daily atmospheric transmissivity of solar radiation, rδ, and daily precipitation, pd.
We also calculated the monthly atmospheric transmissivity of solar radiation τm, which is defined as the ratio of the monthly mean observed S to the monthly mean of TS0. Figure 4 shows the relation between τ m and monthly mean precipitation rate, p m (mmd−1), which is monthly precipitation divided by the number of days in the month. There is a favorable correlation between τ m and p m, and the approximation of the relation between them is:
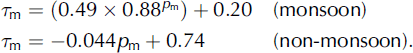
Equation (2) is obtained by weighted least squares. Weight is given as the reciprocal of the number of monthly data at the observation sites (e.g. weight at July 1st glacier is 1/17 in the monsoon season and 1/21 in the non-monsoon season; see Table 1). The minimum value of τ m was set as 0.2 when estimating τ m by Equation (2), because of the convergence of τd toward about 0.2 with the increase of pd.

Fig. 4. Monthly atmospheric transmissivity of solar radiation, rm, and monthly mean precipitation rate, pm, in the monsoon season (May-September) and the non-monsoon season (October-April). Solid lines denote the approximate lines expressed by Equation (2).
The τ m in the non-monsoon season tends to be larger than that in the monsoon season when p m is the same, presumably due to the change of atmospheric conditions, such as the concentration of water vapor and other gases and aerosol, main cloud types and the intensity and frequency of precipitation.
We estimate monthly mean solar radiation, Sm,e, by means of Equation (2) and calculated TS0. The S m,e and the observed monthly mean solar radiation, S m,o, are shown in Figure 5. Correlation coefficients of all S m,e and S m,o are 0.92 in the monsoon season and 0.96 in the non-monsoon season. The relation between S m,e — S m,o (ΔS m) and S m,o is shown in Figure 6. The average plus and minus standard deviation (AV±SD), maximum (Max) and minimum (Min) values of AS m at every measurement site are shown in Figure 7. Almost all absolute values of A S m (|A S m |) are <40 W m−2. However, the ranges of ΔS m at D66 and MS3608 are large: 26−52 W m−2 at D66, and −53 to - 83 W m−2 at MS3608. The spatial variation of complex environmental conditions can cause spatial variation in the relation between precipitation and the effect of clouds on transmissivity of solar radiation; and indeed, ΔS m at D66 and MS3608 is excessively large. Therefore, the error of the estimated monthly mean solar radiation by Equation (2) can be significantly large at some places in the Himalaya and the Tibetan Plateau.

Fig. 5. Estimated and observed monthly mean solar radiation at 11 measurement sites. Solid line denotes 1 : 1 relationship. The n and r denote the number of data and correlation coefficient, respectively.

Fig. 6. Estimated minus observed monthly mean solar radiation AS m as a function of observed monthly mean solar radiation.

Fig. 7. Average plus and minus standard deviation (AV ± SD), and the maximum (Max) and minimum (Min) of ΔS m at every measurement site. Cross denotes maximum and minimum values, circle denotes average value, and bar indicates average plus and minus standard deviation.
Impact of errors in precipitation measurement
Systematic errors in the measurement of precipitation are caused by wind-induced bias, wetting loss, evaporation loss, and variances in gauge design (Reference Goodison, Louie and YangGoodison and others, 1998). Even though wetting and evaporation loss can be ignored, the effects of the other two may be significant, particularly when solid precipitation occurs. Precipitation can only be corrected to the values of DFIR or bush gauge at D105. Therefore, precipitation at all other sites was tentatively corrected by means of the following formulas by Reference Kondo and XuKondo and Xu (1997):
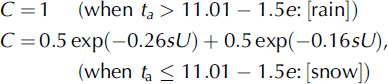
where p d,c and p d,o are the corrected and measured daily precipitation (mm), respectively, t a is daily mean air temperature (°C), e is daily mean vapor pressure (hPa), and U is daily mean wind speed at the height of the gauge orifice (ms−1). According to Reference Goodison, Louie and YangGoodison and others (1998), U is estimated as:

where Uo is the measured daily mean wind speed (m s−1), h and H are the height of the gauge orifice and wind-speed sensor (m), respectively, and z 0 is roughness length: 0.01 m for winter and 0.03 m for summer (Reference Goodison, Louie and YangGoodison and others, 1998). We used a roughness length of 0.01 m for the non-monsoon season and 0.03 m for the monsoon season. The e is estimated as:
where RH is the daily mean relative humidity (%). Measurement points of t a, RH and Uo are the same as those of solar radiation. When C cannot be calculated due to the lack of data on t a, RH and Uo, C is assumed to be 1 during the monsoon season and 0.7 during the non-monsoon season.
Though the error in measuring precipitation by an unheated tipping gauge can cause a critical error, particularly when considerable precipitation occurs under low-temperature conditions, we assumed that this error in monthly precipitation can be ignored, since precipitation is low in the Himalaya and the Tibetan Plateau during the non-monsoon season, and little snow occurs at the precipitation measurement sites during the monsoon season.
As a result of correction by Equations (3–7), precipitation amounts changed at AX010, Ganju La, July 1st and Lugge glaciers and D66. Average and maximum values of the ratios of the corrected precipitation to the measured precipitation are 1.1 and 1.4 in the monsoon season, and 1.5 and 2.2 in the non-monsoon season, respectively. The correction changed Equation (2) to:

where p m,c is the corrected monthly mean precipitation ratio (mmd−1). Though the empirical equation of τ m for the non-monsoon season changes due to the precipitation increase after correction, the equation for the monsoon season is the same as that before the precipitation correction. This is due to the small correction during the monsoon season, with relatively warm (i.e. little snow) and weak wind conditions during this season. The relation between Sm,e and Sm,o, and that between ΔS m and S m,o after precipitation correction are almost the same as those without the correction. Correlation coefficients between S m,e and S m,o after the correction are 0.91 in the monsoon season and 0.96 in the non-monsoon season. The AV ± SD, Max and Min of v at every measurement site after the correction are also almost the same as those without the correction. Though precipitation correction may be inappropriate, its effect on the empirical equation of τ m seems to be small for the monsoon season, since the corrected precipitation changes little during the monsoon season. However, the relation between τ m and p m should be examined again using the correct precipitation amount for the non-monsoon season.
Even though a proper empirical equation for estimating τ m can be obtained, it would be difficult to obtain accurate past precipitation data in mountain regions. Measured precipitation tends to be less than the true value (i.e. τ m tends to be overestimated), because measurement errors are caused by the loss of precipitation by wind, evaporation, etc. We estimated the potential overestimation of τ m and Sm,e when the corrected precipitation was less than the actual precipitation. The magnitude of the overestimation of τ m (Δrm) is estimated from Equation (2) or (8) as:

or

where p m,t is the actual monthly mean precipitation rate (mmd−1). When the ratio of p m,t to p m,c is 1.5 or 2.5, and when the minimum value of τ m is assumed to be 0.2, the maximum value of Δτm is 0.07 or 0.16 for the monsoon season and 0.18 or 0.32 for the non-monsoon season. The monthly mean S0 can be about 480 Wm−2 during the monsoon season and about 430 Wm−2 during the non-monsoon season in the Himalaya and the Tibetan Plateau. Thus, the magnitude of S m,e overestimation can be 35 or 77 Wm − 2 during the monsoon season and 77 or 138 Wm− 2 during the non-monsoon season. The Δτm during the monsoon season becomes maximum when P mc =6.3 mm d−1 (P m,t/P m,c= 1.5) or 4.8 mmd−1 (p m,t/pm,c =2.5). Hence, the input precipitation data need to be highly accurate, particularly when p mc is about 5 mm d−1. Since there is little precipitation (i.e. p m,t and p m,c are small) in the Himalaya and the Tibetan Plateau during the non-monsoon season, Δτm is generally small during this season. However, it should be noted that the magnitude of S m,e overestimation during this season can be excessively large.
Conclusions
We examined the relation between the atmospheric transmissivity of solar radiation and precipitation measured in the Himalaya and the Tibetan Plateau. The monthly mean solar radiation was derived from monthly precipitation, latitude, skyline at the measurement site and time.
Although our approach is not suitable for short-term simulations or for high-spatial-resolution studies due to the poor accuracy of the estimated solar radiation, this approach may be useful for computing solar radiation when it cannot be obtained by other methods. For example, after quality control of re-analysis or GCM precipitation data, our method may be helpful to estimate the spatial variations of this solar radiation index over large areas. Since precipitation and temperature are obtainable from ice cores and tree rings in the Himalaya and the Tibetan Plateau (e.g. Reference Yao and ThompsonYao and Thompson, 1992; Reference Thompson, Mosley-Thompson, Davis, Lin, Henderson and MashiottaThompson and others, 2003; Reference Zhang, Cheng, Yao, Kang and HuangZhang and others, 2003), this approach will be useful to evaluate the paleo-condition of glacier mass balance from limited proxies.
Acknowledgements
This study is based on data obtained by the Japan-Nepal joint research Glaciological Expedition in Nepal (GEN); the China-Japan joint project Cryosphere Research in Qingzang Plateau (CREQ); the Japan-Bhutan Joint Research on the assessment of Glacier Lake Outburst Flood in Bhutan; the Oasis project (Historical evolution of adaptability in an oasis region to water resource changes) promoted by the National Institute for Humanity and Nature, Japan; and GAME-Tibet, which is a regional experiment of the GAME (GEWEX (Global Energy and Water Cycle Experiment) Asia Monsoon Experiment). We express our sincere thanks to all members participating in these projects.










