1. Introduction
The Intergovernmental Panel on Climate Change notes that “Of all the terms that enter the sea level change equation, the largest uncertainties pertain to the Earth's major ice sheets. Relatively small changes in these ice sheets could have major effects on global sea level, yet we are not even certain of the sign of their present contribution” (Reference Warrick, le Provost, Meier, Oerlemans, Wood-worth, Houghton, Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996).
Satellite radar altimeters have potential for reducing these uncertainties, and have been employed to estimate recent multi-year elevation changes on the Greenland ice sheet (Reference Zwally, Brenner, Major, Bindschadler and MarshZwally and others, 1989; Lingle and others, 1991; Reference DavisDavis, 1995), and on selected areas of the East Antarctic ice sheet (EAIS) (Reference PartingtonPartington and others, 1991; Lingle and others, 1994; Her/.feld and others, 1997; Reference Yi, Bentley and StenoienYi and others, 1997). A preliminary estimate of mean changes of the surface height over the entire Antarctic ice sheet north of 81.5° S, during a shorter time interval, has been made by Reference Wingham, Ridout and ArthernWingham and others (1997), and the accuracy of ERS-1 altimetry on the Amery Ice Shelf has been assessed by Reference Phillips, Allison, Coleman, Hyland, Morgan and YoungPhillips and others (1998).
Prior to the 1991 launch of ERS-1, orbital coverage extending to 72.10 Ν and S was provided by Seasat, which flew for 3 months during 1978, and Geosat, which Hew from 1985 through 1989. This resulted in a swath of altimeter coverage relatively near the EAIS margin (Fig. 1; see also Zwally and others, 1983). ERS-1 and, more recently, ERS-2 provide altimeter coverage to 81.5° S, but the time interv al since 1991 is still short relative to the times needed for measurement of mean changes of surface height on the Antarctic ice sheet. The altimeter time scries north of 72.10 S, however, is becoming long enough (15 years, through 1993) for measurement of regional mean changes of the surface height that may be representative of longer-term trends.
We estimate the multi-year mean changes of surface height on the EAIS sheet north of 72.1 S (1, using the met hod of orbit crossover analysis between Seasat (1978), the Geosat Geodetic Mission (CM, 1985-86), the Geosat Exact Repeat Mission (ERM, 1987-88) and ERS-1 (1991-93).The changes are measured on a same-season basis to minimize the effects of spurious seasonal changes in backscatter. The surface height measurements from all three satellites are referenced to JGM-2 orbits and the World Geodetic System 1984 (WGS84) ellipsoid. The crossover analyses are carried out using altimetry corrected for slope-induced errors and, for comparison, altimetry not corrected for slope-induced errors. Errors caused by surface slopes greater than the 0.65° half-beamwidth of ERS-1, which has the narrowest beamwidth of the three satellites (Partington, 1998), are minimized by using only height data from above 1500 m.
2. Sources of error and uncertainty definitions
Regional elevation changes on ice sheets estimated using altimeter crossover differences between different satellites are subject to errors with causes including (i) the relatively high random noise levels present in ice-sheet altimetry, caused primarily by undulating, sloping surfaces (e.g. Lingle and others, 1990, 1994; Reference HerzfeldHerzfeld and others, 1993); (ii) differences in the corrections for atmospheric effects; (iii) differences in pointing stability, which can cause differences in the mean range measured to the surface (Partington, 1998); (iv) different altimeters having different beamwidths, which results in heights derived from the leading edge of the retracked return pulse representing slightly different areas of the illuminated topography on sloping surfaces; (v) other instrumental differences on board the satellites; (vi) the nature of the rctracking method (Davis, 1995,1997); (vii) regional surface slopes exceeding the half-beamwidth of the altimeter with the narrowest beamwidth, which occurs near the margins of ice sheets (Partington, 1998); (viii) systematic, geographically correlated ascending descending bias among the orbits of a particular satel-lite (intrasatellite orbit bias); and (ix) additional systematic, geographically correlated bias among the orbits of different satellites (intersatellite orbit bias). These error sources are minimized or otherwise taken into account in the analysis below.
In the numerical results tabulated here, the “±” uncertainty ranges represent the propagated random errors, i.e. 1 standard deviation (σ) of the mean for the crossover results, propagated using standard methods (e.g. Reference Moffitt and BouchardMoffitt and Bouchard, 1965, p. 163-168). These uncertainties are stated as “ ±3σ of the mean” for the end results (e.g. Tables 1-4). The systematic inlersatellite radial biases estimated from crossover differences on the ALW sea ice also have random components, which are propagated through the bias corrections using the same methods. The numerical results stated in terms of a range of values (e.g. in the abstract and section 11) represent the total range from lowest value less 3σ to highest value plus 3σ.
3. Data selection
The data are obtained as level two along-track surface heights and ancillary data from the ice-sheet altimetry group at NASA Goddard Space Flight Center (GSFC)/ Hughes STX Corp., Greenbelt, MD, where processing of ice-sheet altimetry is carried out by H.J. Zwally and colleagues. Only the height measurements are selected having properly-applied corrections for: (i) retracking, (ii) the ionosphere, (iii) the troposphere, and (iv) the solid-earth tide, as indicated by the data-status flags. The retracking method is GSFC version 4 (v.4), which is an improved version of the method described by Reference Martin, Zwally, Brenner and BindschadlerMartin and others (1983) (sec Davis, 1997). All data are corrected to JGM-2 orbits, using the orbit increments supplied on the tapes. Surface heights not having JGM-2 corrections are rejected.
The data are then separated into orbits and, along each orbit, into contiguous segments of data, i.e. sequences of height measurements without missing data representing loss of track by the altimeter. The contiguous data segments are indexed. A contiguous segment is defined as at least five height measurements without a gap; data segments consisting of fewer than five sequential measurements are rejected. This criterion is applied to exclude marginal data from areas where the altimeter maintains lock only with great difficulty. The data are checked for distinct, successive Iatitude/longilude coordinates and time-sequencing errors. Sequential data having duplicate latitude/longitude coordinates are also rejected. (This problem has been mostly eliminated in the v.4 data, and occurs only rarely.)

Fig. 1. Locations of the first 10 000 orbit crossover points between Seasal, and Geosat, throughout the area north of 72.1° S and above 1500 m.
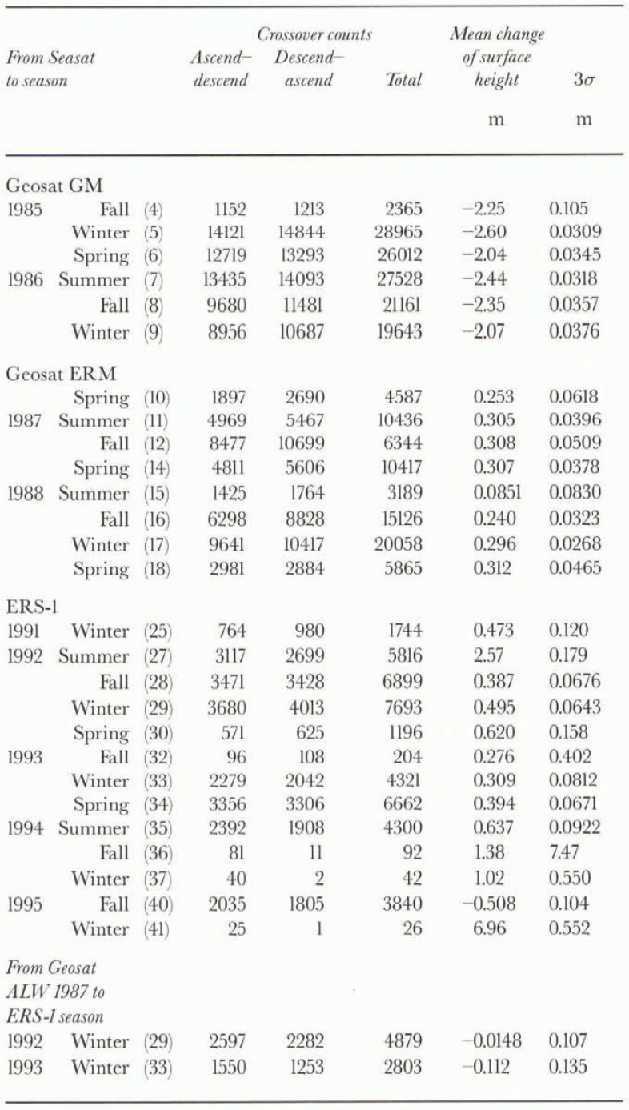
Table 1. Crossover results on the continental ice sheet (1, computed using altimetry corrected for slope-induced errors
Data over the ice sheets were acquired by ERS-1 with the altimeter operating roughly 50% of the time in ocean mode and the remainder of the time in ice mode. The latter was introduced to enable the altimeter to maintain lock more reliably over the ice sheets, reducing the incidence of data gaps at the expense of yielding data with lower height resolution. The ice-mode data were found to yield poor results, however, characterized by large scatter, in crossover analyses with the Seasat and Geosat altimeter data, which were acquired entirely in ocean mode (Lingle and Voroni-na, 1996). (The earlier altimeters did not have an ice mode.) Only ocean-mode data were therefore selected from the ERS-1 tapes, for consistency with the earlier altimetry.
Corrections for slope-induced errors were applied to the data used to carry out the crossover analysis shown in 9ur and Table 1. The slope corrections, computed using the method of Reference Brenner, Bindschadler, Thomas and ZwallyBrenner and others (1983), are available on the v.4 tapes. For this analysis, height measurements not having valid slope corrections (according to the status flags) were rejected, which somewhat reduced the number ofacceptable Seasat vs Geosat ERM and Seasat vs ERS-1 crossover differences (cf. tables Table 1 and Table 2). The crossover analysis was also carried out using height measurements that were not corrected for slope-induced errors (Fig. 10; lable 2).
4. Crossover computations
Potential orbit crossover points are first identified by computing great circle coefficients for all of the indiv idual contiguous data segments, along-orbit. The crossing point between two data segments, if it exists, is then found by simultaneous solution for the common point : in the Southern Hemisphere) of the great circle equations for the two segments. If a crossing point is found, the simultaneous solution is iterated by choosing points progressively closer to the initial estimate of the crossover location, a necessary step because an orbit ground track of finite length does not form an exact great circle because of rotation of the earth beneath the satellite. Each of the two crossing segments is then identified as cither ascending (latitude increasing northward with time) or descending (the reverse). If the crossing segments are either both ascending or both descending, the potential crossover point is rejected for reasons related to cancellation of orbit bias (sec below). If any of the four height measurements bracketing the crossover point lies well outside the elevation range for the entire ice sheet, defined as -100 to 5000 m, the potential crossover point is also rejected at this stage. (A small number of these extreme outliers were identified in the Seasat data.)
The elevations, times and differences at the exact crossover location are then determined by linear interpolation between the bracketing data points. If the time values of the nearest data points along-orbit are not sequential (20 Hz for the ERS-1 ice-sheet altimetry; 10 Hz for the Geosat and Seasat ice-sheet altimetry), the crossover point is rejected at the interpolation stage. That is, crossover points falling within data gaps of any size are not accepted. Crossover differences satisfying all of the above criteria are retained, along with their associated locations and times.
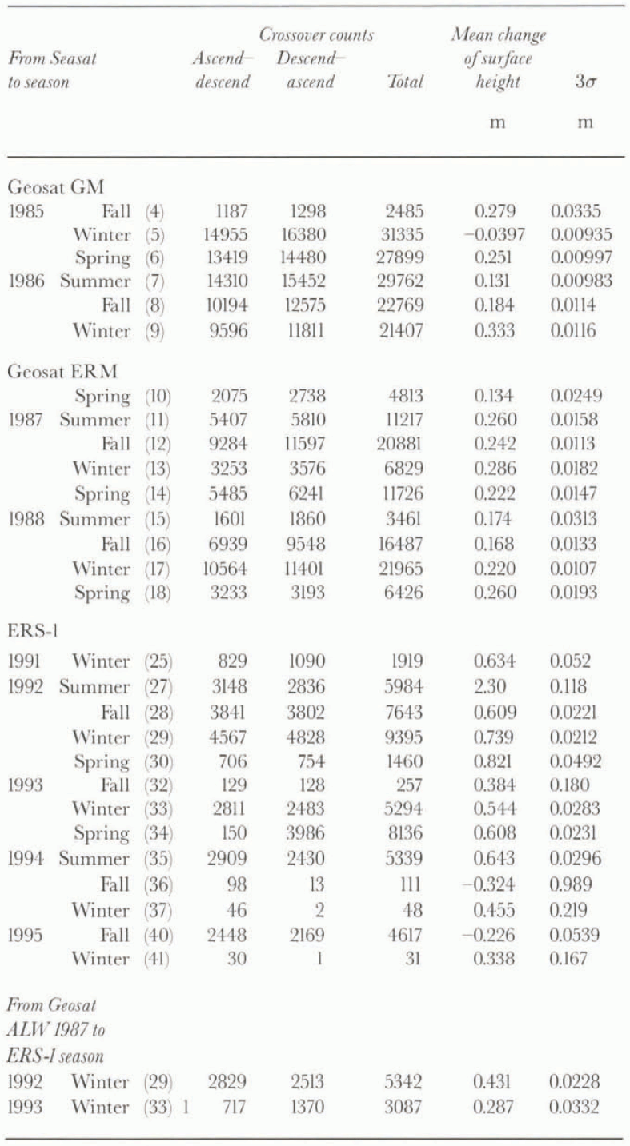
Table 2. Crossover results on the continental ice sheet (1, computed using altimetry without corrections for slope-induced errors
5. Statistical Analysis
Geographically correlated intrasatellite orbit bias is cancelled by computing the mean ascending minus descending crossover difference and the mean descending minus ascending crossover difference independently, for each of the sequential 3 month “seasons". The regional change between Seasat and a given subsequent season is then taken as the mean of the two mean values. For the results presented here, crossover differences are taken between the orbits of Seasat (only) and the orbits of the subsequent satellites. Individual crossover differences are taken as the surface height measured from the later orbit less the height measured from the earlier orbit. If the regional mean intrasatellite ascending descending bias for Seasat is b1 and for a later satellite b2, and if the regional mean intcrsatellitc orbit bias between the two sets of orbits is B, then this procedure results in cancellation of b1 and b2 leaving only R, which must be estimated independently. Estimates of B, combined with other sources contributing to intersalellile radial bias such as instrumental bias, are made using the offshore austral late-winter (ALW) sea ice as a geoid-parallel reference surface (see section 7).
The number of crossover differences from ncar-coasial areas with regional surface slopes in excess of the 0.65° half-beamwidth of ERS-1 is minimized by applying an elevation criterion: only crossover differences from areas above 1500 m are used in this analysis. Crossover differences from steeper areas tend also to be eliminated, mostly, by the 3σ edit procedure described below, because these near-coastal areas are characterized by relatively high noise levels (Lingle and others, 1990).
An iterative 3σ edit is used to eliminate outliers among the crossover differences, because this procedure does not bias the mean with respect to zero. Figure 2, which is a log-linear histogram, shows the distribution of all crossover differences that are potentially acceptable, according to the above criteria, computed hetween the ALW season ofSeasat (1978) and a subsequent ALW of the Geosat ER M (1987). The outliers range from about +180 to -450 m. Figure 3, which shows the distribution after application of the 1500 m height criterion, also shows that the most extreme outliers are eliminated by this height criterion alone since they are located on or near the coast. The 3σ edit consists of computing the mean and standard deviation (σ), discarding crossovers that are more than ±3σ from the mean, then recomputing the mean and σ. This procedure is iterated until the mean and σ converge to constant values, which usually requires about 7-9 iterations. Figure 4, which is a log-linear histogram of the distribution of the same crossover differences after application of both the height criterion and the 3σ edit, shows that the outliers are effectively eliminated. The mean crossover difference in this case is +0.29 m, the median is +0.28 m, and σ is 0.5 m. Figures 2-4 are typical of the distributions for Seasat “crossed with” the ALW seasons of Geosat.
Figures 5-7 show an analogous set of crossover distributions for Seasat crossed with ALW 1992 of ERS-1. The initial spread (5 is larger (about +220 to -950 m), and at each stage the distribution is less symmetrical than for Seasat crossed with Geosat ALW 1987. in Figure 7, the mean and median are 0.65 and 0.67 m, respectively, while σ is larger than in 4ur by 30% (0.65 vs 0.50 m). This less symmetrical distribution of the crossover differences for Seasat crossed with ERS-1 vs Seasat crossed with Geosat, illustrated in Figures 5-7 vs Figures 2-4, is typical of Seasat crossed with the other ALW seasons of ERS-1 and Geosat.
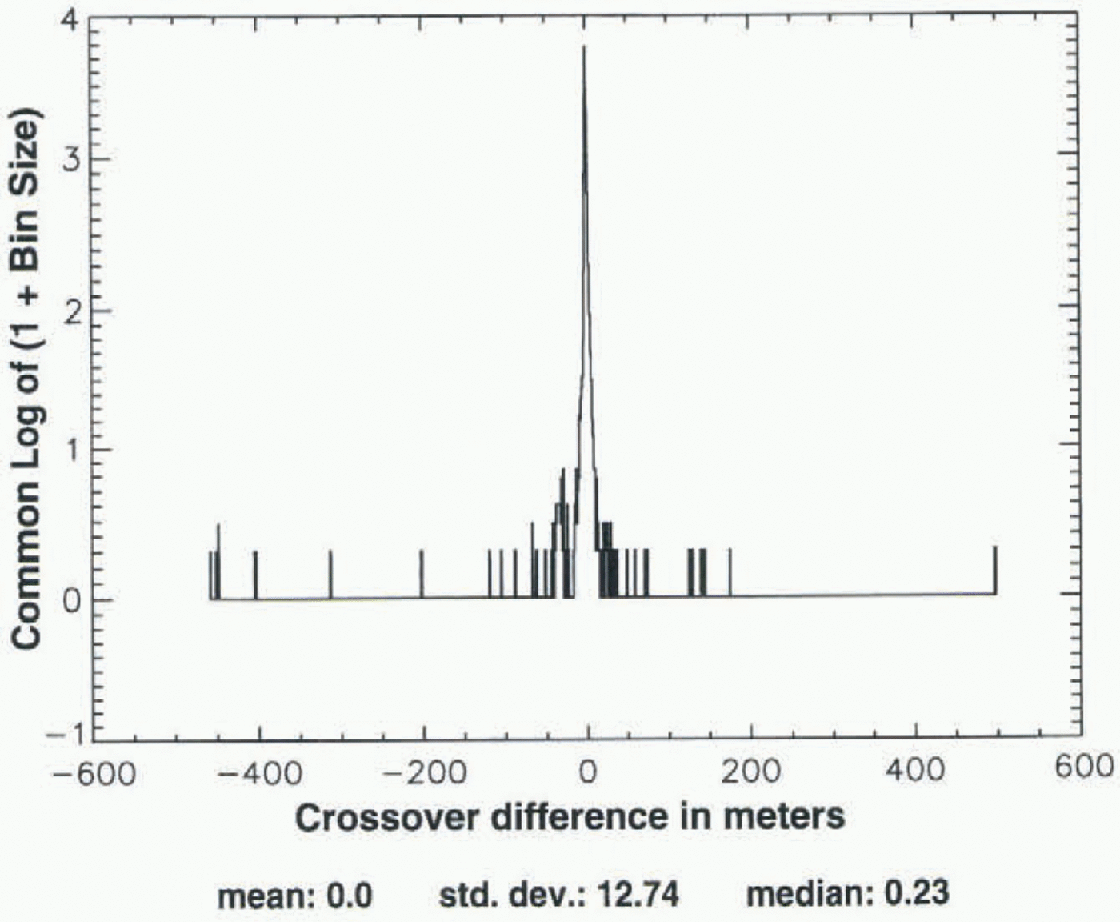
Fig. 2. Log-linear histogram showing distribution of all crossovers between Seasat and ALW 1987 of the Geosat KRAI, throughout the area shown in 1ur (no elevation criterion).
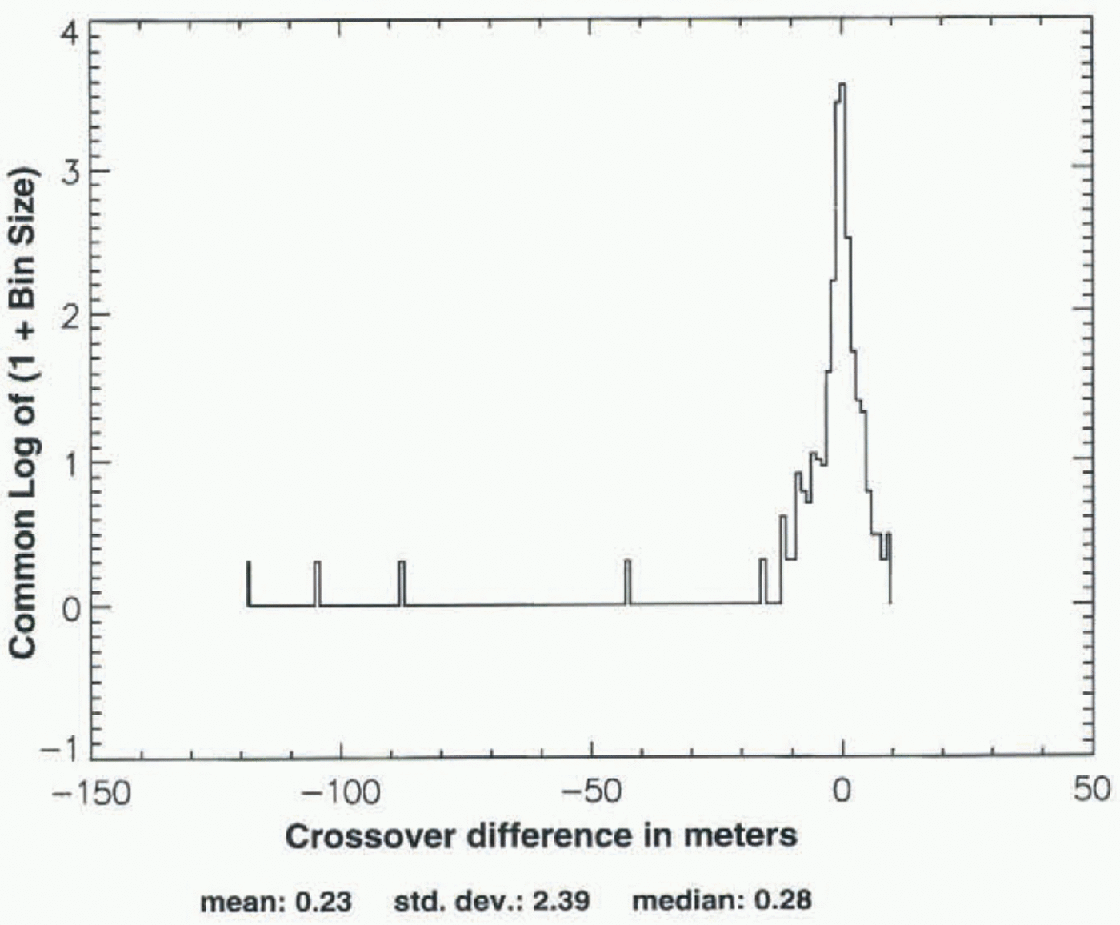
Fig. 3. Distribution of the Seasat-Geosat ERM (ALW 1987) crossovers shown in Figure 2, with only those from above 1500 m selected.

Fig. 4. Distribution of the Seasal Geosat ERM (ALW 1987) crossovers shown in 3ur after iterative 3σ edit.
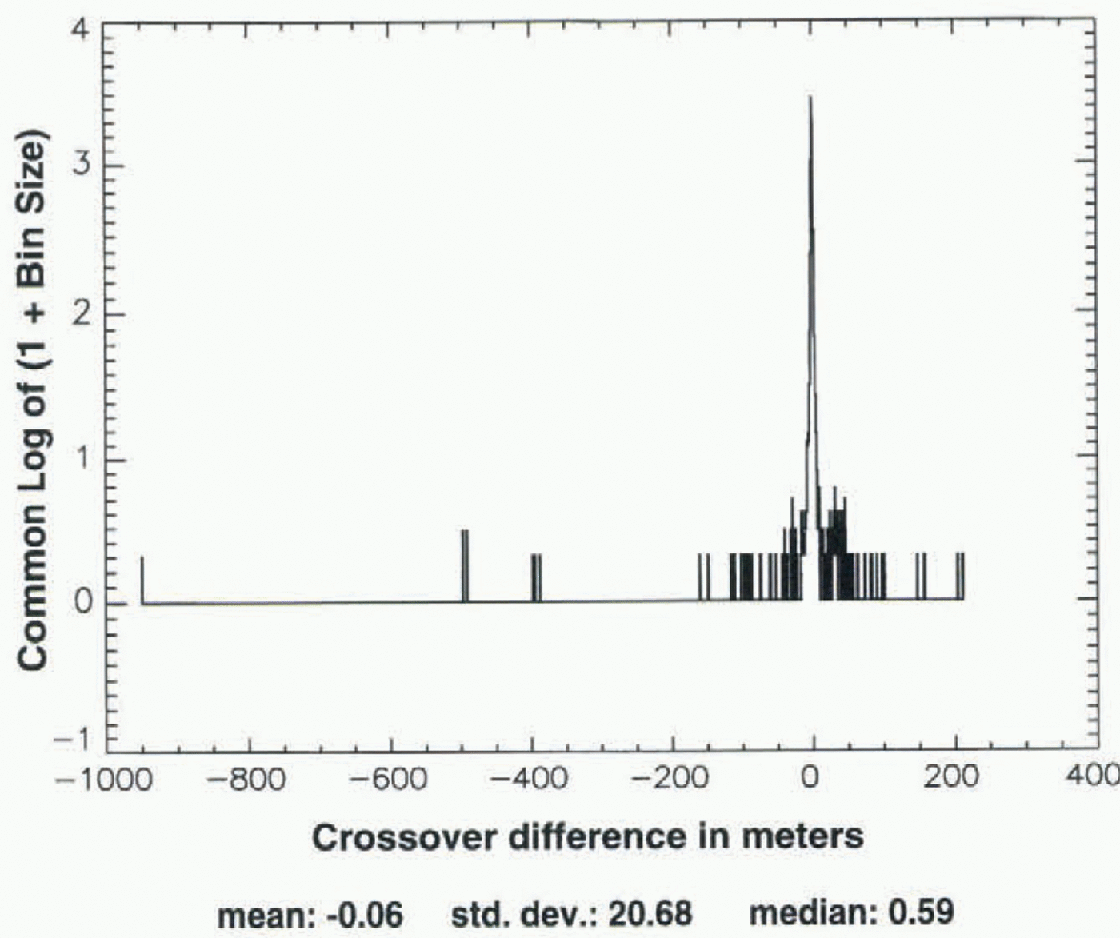
Fig. 5. Log-linear histogram analogous to Figure 2, but showing distribution of all crossovers between Seasal and ALW 1992 (f ERS-1, throughout area shown in 1ur (no elevation criterion).
Figure 8 is a histogram showing the distribution of sea-ice crossover differences, with the crossover analysis carried out over the region shown in Figure 11, for the case of Seasat ALW 1978 crossed with Geosat ALW 1987, after application of the data-selection criteria described above (but no elevation criterion), followed by an iterative 3σ edit. Note that the histogram ofFigure 8 is not quite as symmetrical as the continental-data histograms shown in figures 4 and 7, but the mean is similar to the median (cf. figs 4 and 7), and the standard deviation (0.62 m) is similar to the standard deviations of figures 4 and 7, as is the total range of crossover differences (-1.6 to +2.2 m). The sea-ice crossover analysis is discussed further in sections 7 and 10.
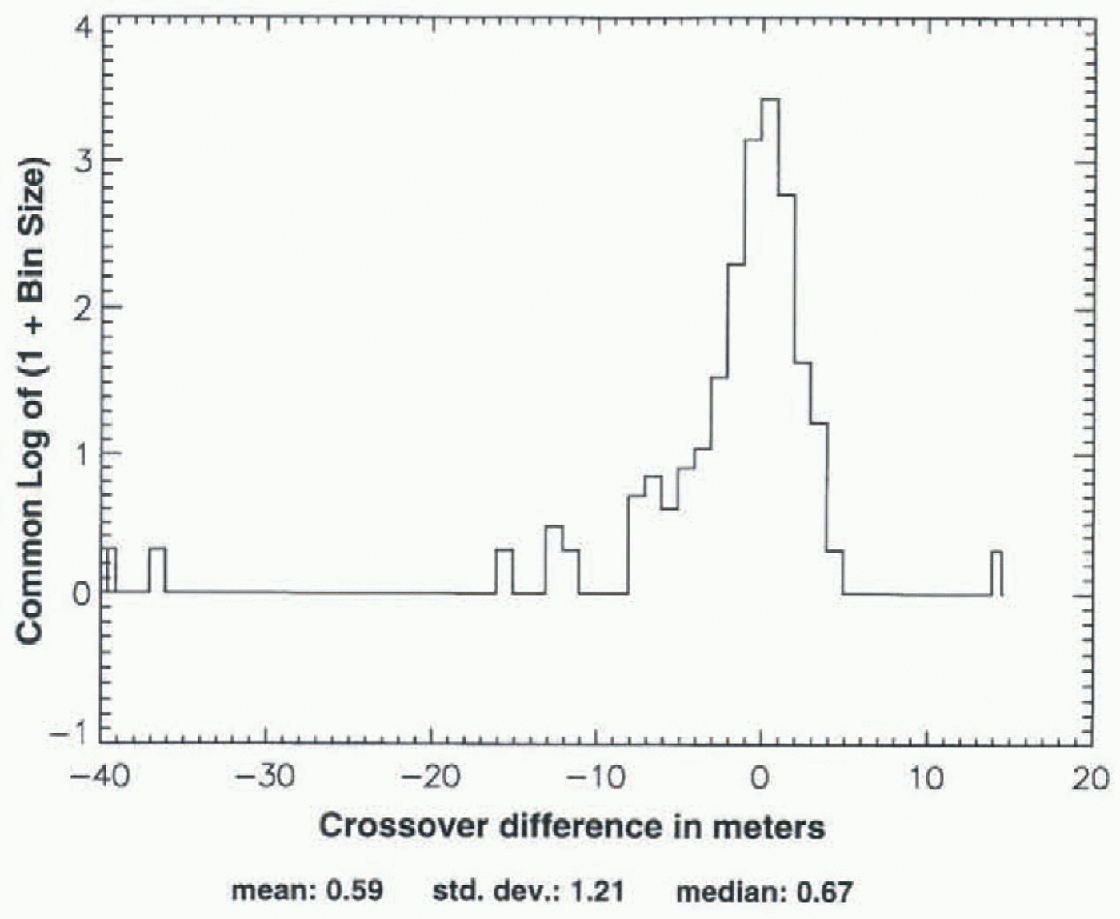
Fig. 6. Distribution of crossovers, Seasat to ERS-I (ALW 1992), with only those from above 1500 m selected from the distribution shown in Figure 5.
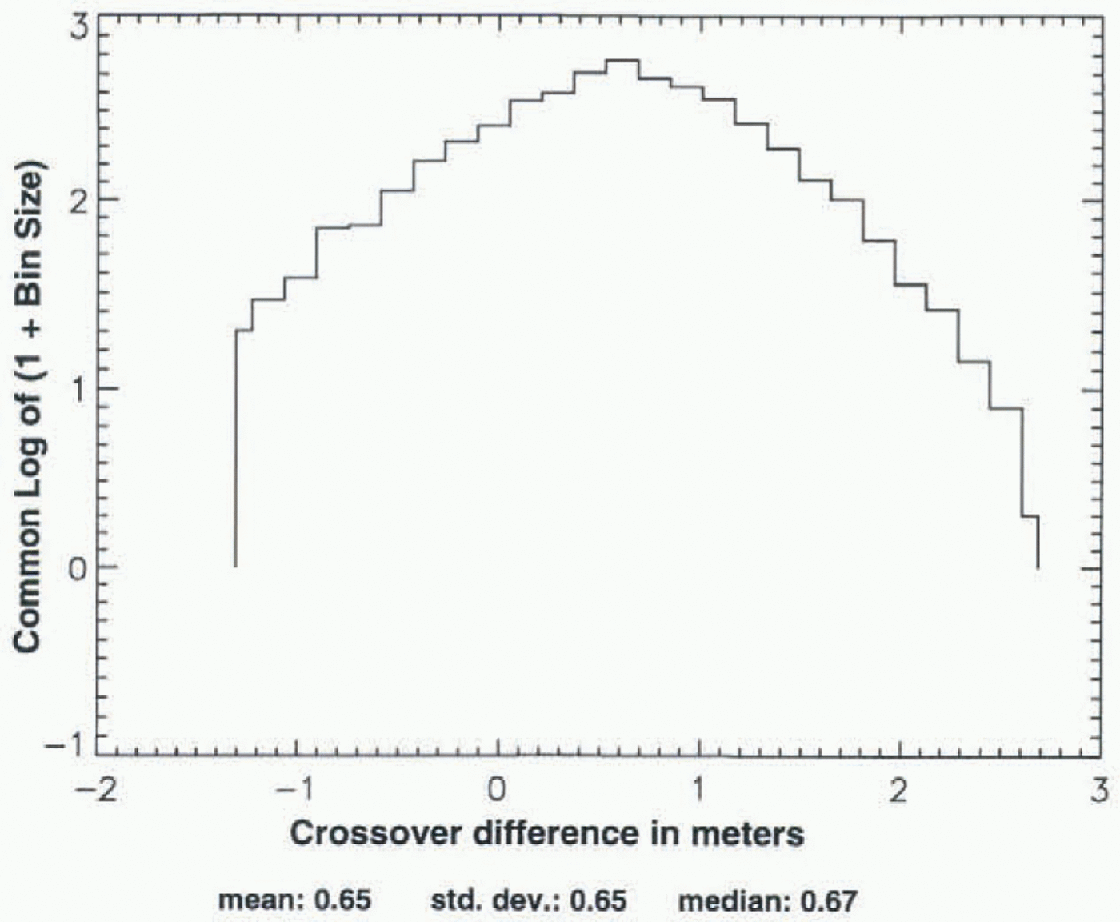
Fig. 7. Distribution of the Seasat to ERS-1 (ALW 1992) crossovers from Figure 6, after iterative 3σ edit.
6. Multi-Year Crossover Results
Figure 9 and Table 1 the results of the crossover analysis carried out using slope-corrected height measurements. The crossover differences were sorted as a function of time, such that the Seasat orbits of ALW 1978 (10 July-9 October) were, in effect, crossed with the subsequent sequential seasons (3 months each, defined in accordance with the preceding dates) of the Geosat ERM and ERS-1. The zero datum represents the mean surface height at the time
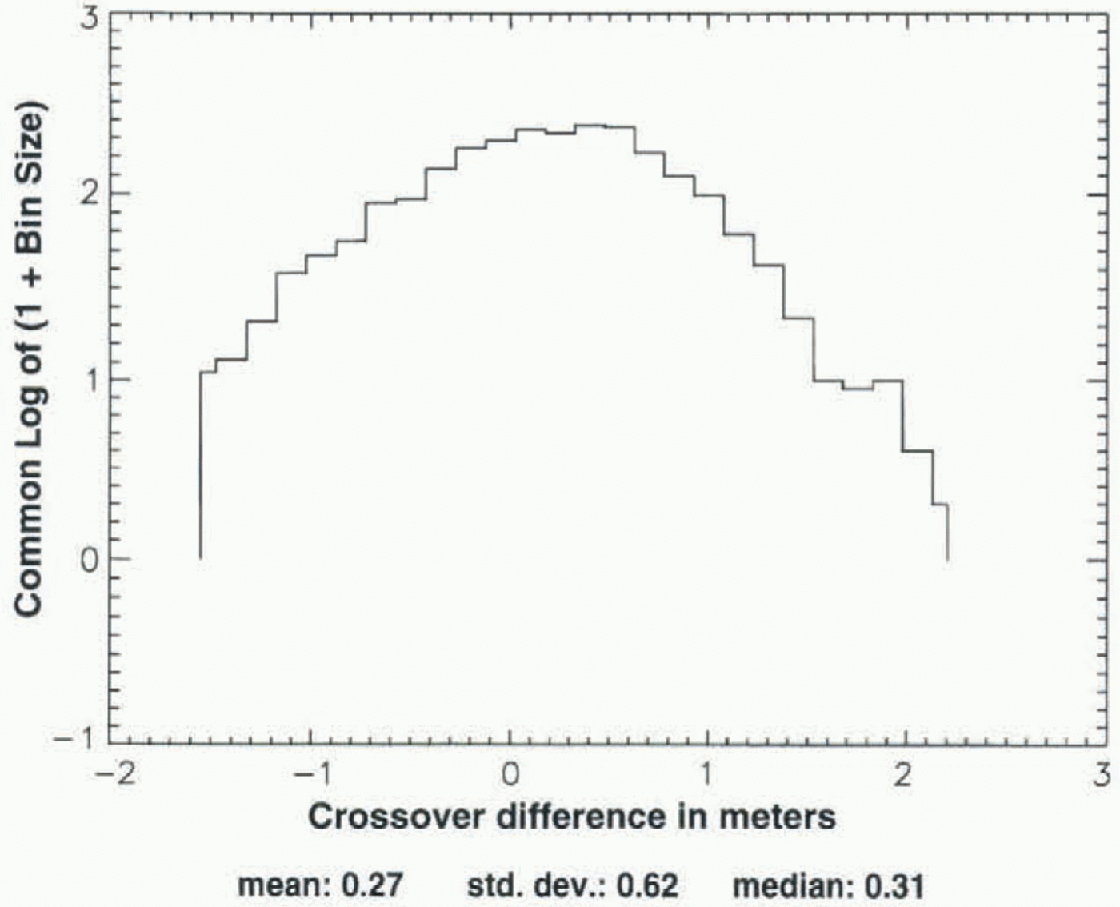
Fig. 8. Distribution of sea-ice crossovers, Seasat-Geosat ERM (ALW 1987), for area shown in Figure 11, after application of 3σ edit.
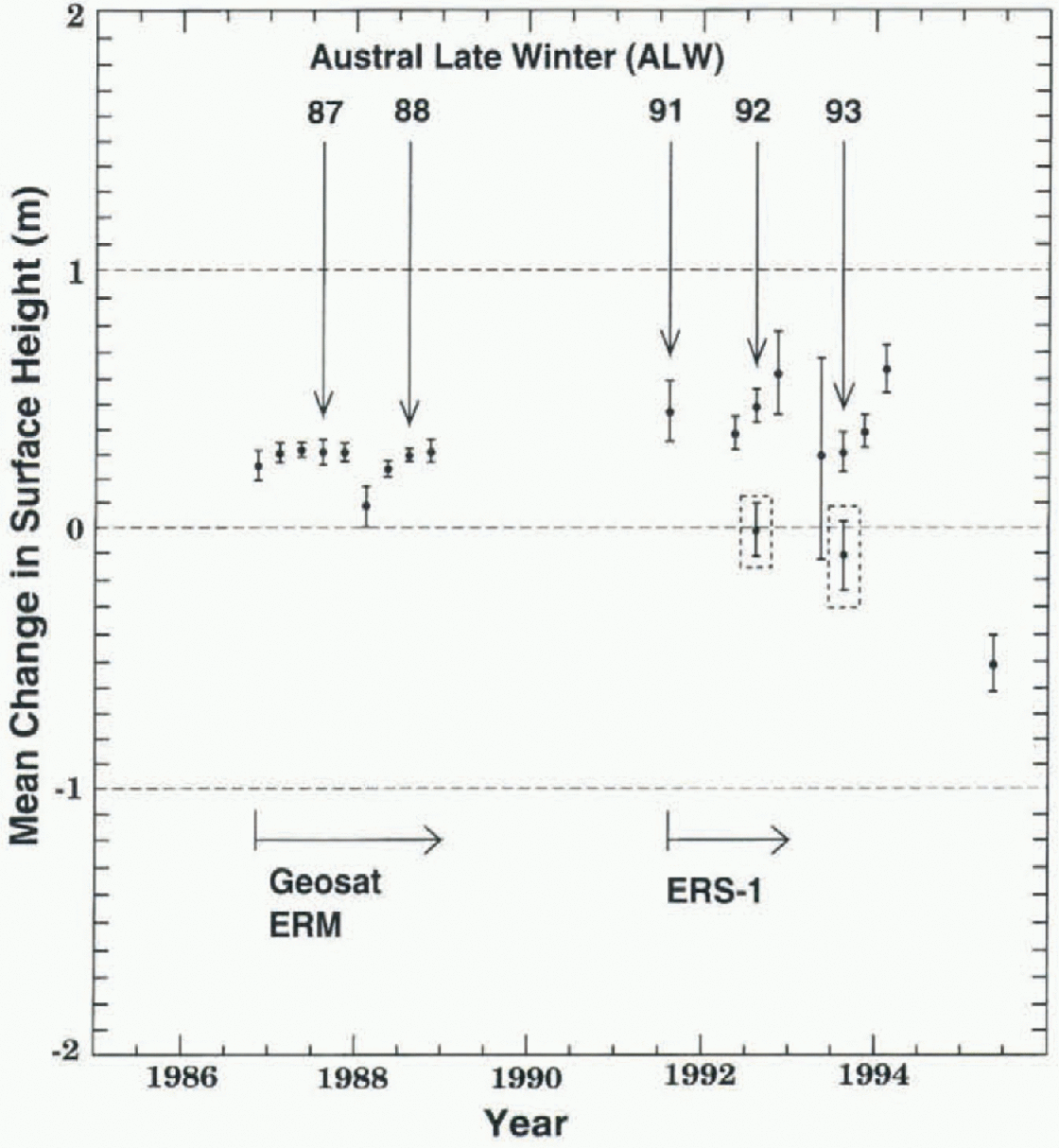
Fig. 9. Results of slope-corrected Seasat altimetry (ALW 1978) crossed with slope-corree ted altimetry from the subsequent austral seasons of the Geosat ERM and ERS-1. The ALW seasons corresponding to the Seasat time-frame are marked with arrows. The error bars represent 3σ of the mean. Seasons 4-9 of Table 1 omitted, as are seasons 36, 37 and 4L These results are not adjusted for intersatellite radial bias. (See text.)
of Seasat. Each dala point represents the mean change of the surface height throughout the area shown in Figure 1, between ALW 1978 and the season at the time of the data point, as measured by the crossover differences. A positive change means the surface was higher, on average, than during ALW 1978. The labeled vertical arrows (ALW 1987, etc.) indicate the same-season changes, i.e. the points corresponding to the ALWs of the years after 1978. The error bars represent 3σ of the mean for the crossover differences in each case. The seasons having the largest number of acceptable crossover differences after the 3σ edit, as described above, thus generally have the smallest error bars. The Seasat crossed with Geosat GM results are excluded from this plot, because the slope corrections for the Geosat GM data appear to be characterized by significant systematic errors (compare the first six values of the “Mean change of surface height” column in Tabel 1with the rest of the same column in Table 1, and with the analogous first six values in Table 2). Also omitted from 9ur are seasons with an exceptionally small number of acceptable crossover differences (which passed the selection criteria), with gross imbalance between the number of ascending-descending vs descending-ascending crossovers. These seasons include austral late fall 1994, ALW 1994, and ALW 1995 (see Table 1).
Figure 10 and Table 2 show, for comparison, the results of the crossover analysis carried out using surface heights not corrected for slope-induced errors. 10ur does not differ dramatically from Figure 9. The average mean change of the surface height for Seasat crossed with all seasons of the Geosat ERM (seasons 10-18 in Table 2) is 0.22 m. The average of the same seasons computed using slope-corrected altimetry (seasons 10-18 in Table 1) is 0.27 m. The average-change of the surface height for all seasons of Seasat crossed
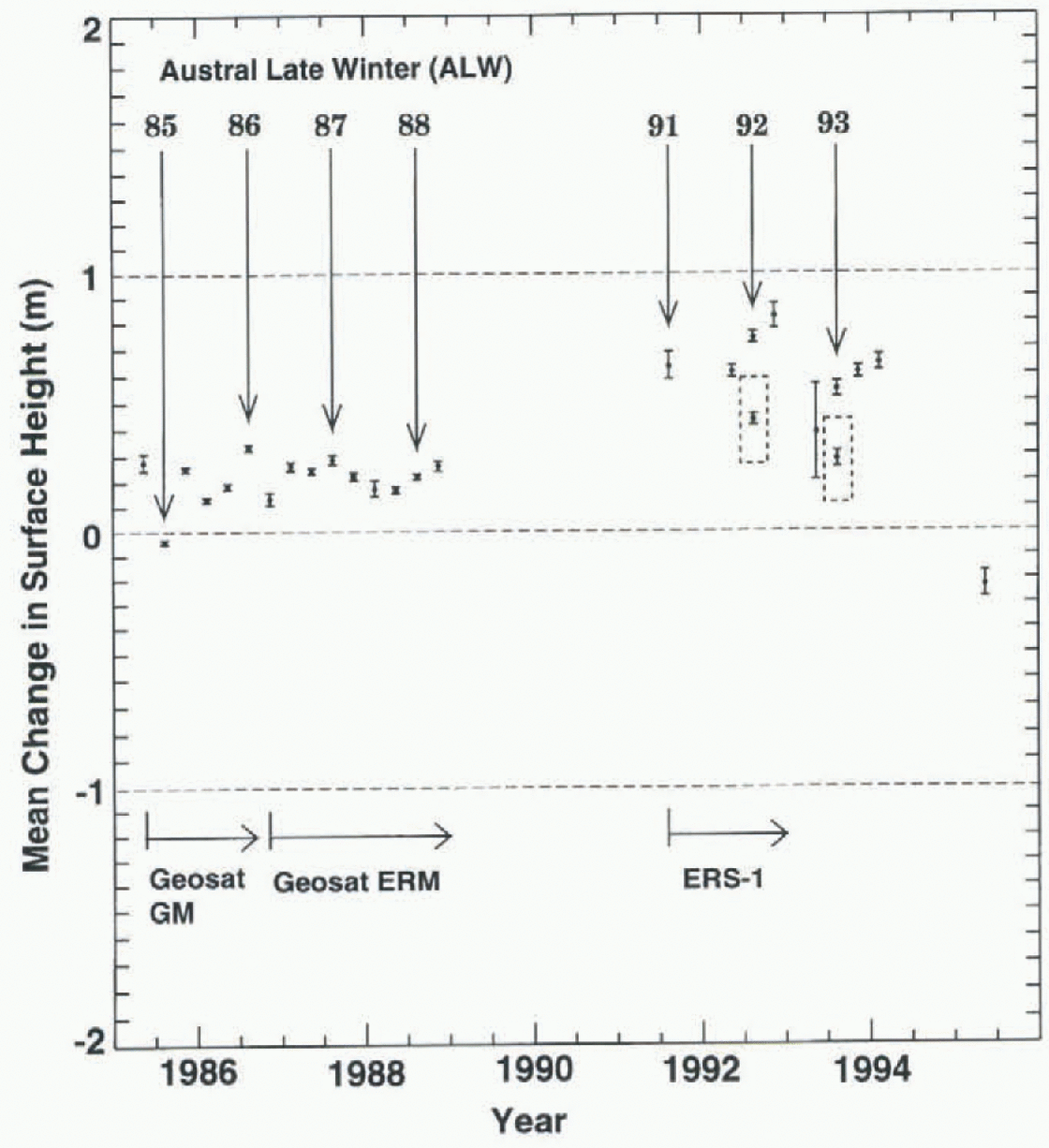
Fig. 10. Results of non-slope-correcled Seasat altimetry (ALW 1978) crossed with non-slope-corrected altimetry from the subsequent austral seasons of Geosat and ERS-1. The error bars represent 3σ of the mean. Seasons 36, 37 and 41 of Table 2are omitted. These results are not adjusted for intersatellite radial bias. (See text.)
with ERS-1, omitting those with extreme values (seasons 27 and 40) and those with statistically insignificant numbers of crossover differences (seasons 36, 37 and 41) is 0.62 m. The average of the same seasons computed using slope-corrected altimetry is 0.45 m. in a case where the crossover differences occur along exact-repeat orbits, such as between Seasat and the Geosat ERM, it would seem that slope corrections should make no difference, because of constant (or near-constant) correlation between the altimeter surface and the “real” Surface. figures 9 and 10 and tables 1 and 2 show that this is almost (though not exactly) the case. Where the crossover differences are among orbits not exactly repeating, and also having differing inclinations, as in Seasat vs ERS-1, it would seem that not slope-correcting the data might lead to substantial errors in the results. The difference between the slope-corrected vs not slope-corrected cases for Seasat crossed with ERS-1 is certainly greater than for Seasat crossed with the Geosat ERM, but the difference is not of large magnitude.
Finally, ALW 1987 of Geosat was crossed with ALWs 1992 and 1993 of ERS-1, using the continental ice-sheet data from the area shown in Figure 1. This was done in spile of the shorter 5-6 year time interval, because the analogous sea-ice crossover analyses (ALW 1987 to ALWs 1992 and 1993; area shown in Fig. 11) were carried out using sea-ice altimetry retracked using the GSFC v.4 method, as were the continental ice-sheet data, thus enabling greater confidence in the use of the sea ice as a reference surface. (See next section, and note that the Seasat sea-ice altimeter data were not retracked, although the histogram shown in 8ur suggests that these data are relatively “well behaved” after the iterative 3σ edit.) The results of this crossover analysis, carried out over the continental ice sheet using both slope-corrected altimetry and altimetry not corrected for slope-induced errors, are shown as the last two lines of Tables I and 2, respectively. These results are also shown as the points inside dashed boxes in figures 9 and 10. Note that for these points the zero datum represents the mean surface height at the time of Geosat ALW 1987 (not Seasat ALW 1978).

Fig. 11. Locations ofcrossover points on ALW sea ice, Seasat, to ERS-1 (ALW 1992). The mask used to define the sea-ice region was digitized from Reference Gloersen, Campbell, Cavalieri, Comiso, Parkinson and ZwallyGloersen and others (1992). See Table 3
7. Sea Ice: a reference surface
The results of the crossover analyses shown in figures 9 and 10 appear to indicate that the mean surface was generally higher during the Geosat years (1985—89) than during ALW 1978 (Seasat), and somewhat higher still during the early ERS-1 years (1991-93) relative to Seasat. The ALW 1987-89 changes during the Geosat ERM years (Fig. 9; Table 1), however, do not suggest a rising surface, nor do the ALW 1986-88 changes of the Geosat GM and ERM (Fig. 10; Table 2). Similarly, the ALW to ALW changes during the ERS-1 years do not suggest a rising surface for those seasons having sufficient crossover differences to be considered statistically significant (ALWs 1991-93 in tables 1 and 2). This implies that the apparent increases of the surface height from Seasat to Geosat and ERS-1, respectively, may be expressions of intersatellite radial bias, defined, as noted above, as the combined effect of intersatellite orbit bias, inst rumental bias and other factors contributing to differing measurements of the same surface by different altimeters.
The large expanses of sea ice surrounding Antarctica during the ALWs (Fig. 11; sea-ice boundary defined from Gloersen and others, 1992) form a potential geoid-parallel reference surface for inland ice-sheet altimetry. The area-averaged thickness of undeformed East Antarctic sea ice, which comprises approximately 70-80% of the sea-ice area with in the 60-150u Ε sector (10, is about 0.5 m (Reference Allison and WorbyAllison and Worby, 1994; Worby and others, in press). The sea-ice surface is thus within roughly 0.05 m of sea level over most of its area due to flotation, and the multi-year mean rate-of-change of the surface height measured by altimeters should be close to zero. Apparent vertical changes in the ALW sea-ice surface measured between satellites should thus constitute a measure of intersatellite radial bias.
In practice, however, sea-ice altimeter data are relatively noisy (see Reference LaxonLaxon, 1994). The reasons for this include spatial variation in the dielectric properties of the surface caused by leads, and phenomena such as penetration of ocean swells for hundreds of km into the pack from the open sea. (According tojosberger and Mognard (1996), the highest waves worldwide occur, on average, in the Southern Ocean north of the East Antarctic pack.) Worby and others (in press) point out that this causes surface Hooding due to water squirting up between floes within swell-affected regions, particularly as the floes are compressed in the troughs. The result is a continuing, spatially varying process of surface flooding followed by refreezing. According to M. O. Jeffries (personal communication, 1997), spatially variable surface flooding is also widespread in the Amundsen-Bellingshausen Seas, although in that region this phenomenon is unrelated to penetration of the pack by ocean swells.
Despite these considerations, we employ crossover differences from the region of ALW sea ice shown in 11ur as a means for estimating the intcrsatellitc radial bias between Seasat and Geosat, Seasat and ERS-1, and Geosat and ERS-1. This is done because the sea ice was at maximum extent during the 1978 time-frame of Seasat. If estimates of intersatellite radial bias were made using altimetry acquired over the ice-free ocean farther north, those estimates would be of doubtful applicability, due to the large distances separating the ice-free ocean from the measurement area (1 on the continent.
The sea-ice data are corrected for ocean tides, as well as the geoidal component of the solid-earth tide. The same data-selection criteria and iterative 3σ edit procedures described above for the inland ice-sheet altimetry were applied. The results, shown in Table 3, indicate an apparent mean increase of the surface height of the sea ice of 0.28±0.03 m between Seasat and the ALW 1987 and 1988 seasons (averaged) of the Geosat ERM. As a check, Geosat ALW 1987 was crossed with Geosat ALW 1988. The mean change of the surface height, as noted in Table 3, was found to be 0.002±0.013 m, which is negligible, indicating that the apparent “step up” of the sea-ice surface between Seasat and Geosat can be taken as an estimate of radial bias between the two satellites.
Table 3. Crossover results computed on the ALW East Antarctic sea ice (11
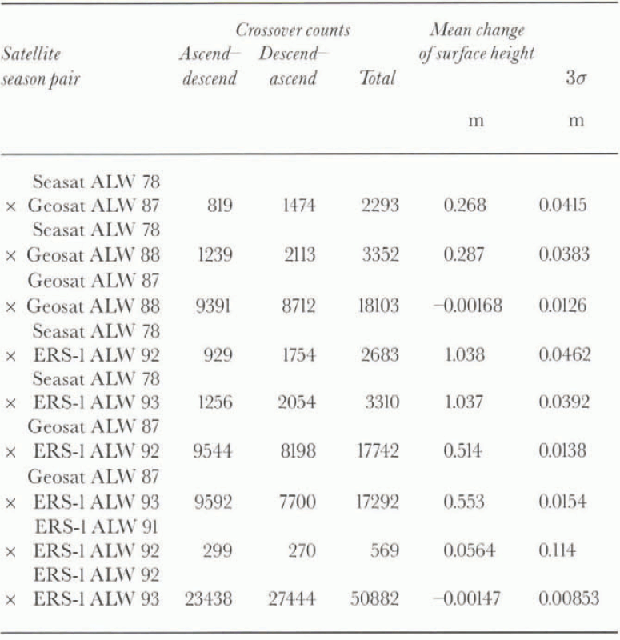
The Seasat sea-ice orbits were then crossed with the ERS-1 orbits from the same region. The results, also shown in Table 3, indicate an apparent mean increase of the sea-ice surface of 1.04±0.03 m, between ALW 1978 and ALW 1992 and 1993 (averaged). Again, as a check, ALW 1991 of ERS-1 was crossed with ALW 1992. The apparent mean change in the surface height was 0.056±0.114 m (table 3), which is small. The number of valid crossover diflcrcnccs between these two seasons is less than optimal, however, so ALW 1992 of ERS-1 was crossed with ALW 1993. The mean change in the surface height was -0.001±0.009 m (table 3), which is negligible.
The Seasat Antarctic sea-ice data have not been retracked, but the Geosat and ERS-1 sea-ice data have been retracked using the GSFC v.4 method, lb test the possibility that the intersatellite sea-ice results are an expression of this, the ALW 1987 orbits of the Geosat ERM were crossed with the ALW 1992 and 1993 orbits of ERS-1 over the same sea-ice area (11. As noted in Table 3, the results show an apparent mean increase of 0.53 ±0.01 m (both seasons averaged) of the sea-ice surface between Geosat and ERS-1. When added to the Seasat to Geosat (apparent) radial bias of 0.28±0.03 m, this implies a total radial bias, Seasat to ERS-1, of 0.81 ±0.03 m (not 1.04± 0.03 m). This, in turn, implies a contribution from non-retracking of the Seasat sea-ice altimetry to the apparent radial bias between the satellites, or, alternatively, a larger instrumental bias between Seasat and ERS-1 than between Seasat and Geosat.
The results of the sea-ice crossover analyses shown in Table 3indicate that the altimeter data referenced toJGM-2 orbits have high consistency for each of the three satellites, but there are significant intersatellite radial biases between Seasat and Geosat, between Seasat and ERS-1, and between Geosat and ERS-1. Between Seasat and Geosat ALW 1986 (table 2), we take this bias to be the average of the entries on the first two lines in Table 3(0.28±0.03m, Geosat surface higher). Between Seasat and Geosat ALWs 1987 and 1988, we use the entries on the corresponding lines in Table 3. Between Seasat and ALW 1991 of ERS-1, we use the average of the Table 3 entries corresponding to the Seasat x ERS-1-1992 and 1993 (1.04 + 0.03 m, ERS-1 surface higher). Between Seasat and ALWs 1992 and 1993 of ERS-1, we use the entries on the corresponding lines in Table 3. An alternative minimum Seasat to ERS-1 bias estimate is also used, calculated analogously, consisting of Seasat to ALW 1987 of Geosat plus ALW 1987 of Geosat to ALW 1992 (also 1993) of ERS-1, from Table 3in the former case, this is 0.78 ± 0.04 m; in the latter case, it is 0.83 ±0.04 m (ERS-1 surface higher).
8. Surface height changes, adjusted for intersatellite radial bias
The adjusted mean rates of change of the surface height on the inland ice sheet are shown in Table 4; note that all values are in mm a−1. They were estimated by choosing the ALW seasons from Table 1(slope-corrected altimetry) and Table 2(altimetry not slope-corrected) for which consistent
Table 4. Mean rates-of-change of surface height (mm a−1), derived from tables 1 and 2 and adjusted for intersatellite radial bias using Table 3
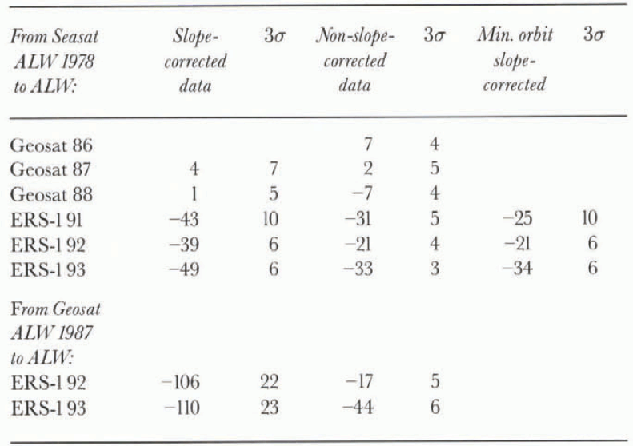
results were obtained for at least two different years, both having a sufficient number of valid crossover differences to be considered statistically significant. The inland ice-sheet results are adjusted using the inlersatellite radial biases estimated from the sea-ice altimetry (table 3), as described above, which were also determined by choosing the ALW seasons for which consistent results were obtained for at least two different years, both having sufficient valid crossover differences. These criteria eliminated ALWs 1994 and 1995 (tables 1 and 2) from consideration. in addition, the slope-corrected results for Seasat crossed with the Geosat GM (ALWs 1985 and 1986) are not used, for the reason stated in section 6.
As noted in the previous section, the Seasat sea-ice altimeter data used to estimate the intersatellite radial bias between Seasat and Geosat, and Seasat and ERS-1, were not retracked. The Geosat and ERS-1 sea-ice altimetry, however, were retracked. This introduces uncertainty as to the reliability of the intersatellite radial-bias estimates derived using the unret racked Seasat sea-ice altimetry, particularly because the total radial bias, Seasat to ERS-1 (about 1.04 m; Table 3), differs from the same bias derived using the sum of the Seasat to Geosat radial bias (about 0.27-0.29 m; Table 3) and the Geosat to ERS-1 radial bias (about 0.51-0.55 m; Table 3). That is, the latter sum gives about 0.8 m for the total radial bias, Seasat to ERS-1. Consequently, crossover analyses were run over the continental ice-sheet area shown in Figure 1, using the altimetry from Geosat ALW 1987 crossed with the altimetry from ERS-1 ALW 1992, and 1993. The runs were carried out using both slope-corrected altimetry and altimetry not slope-corrected. The results appear as the last two lines in tables 1 and 2, respectively, and are also shown as the points enclosed in dashed boxes in figures 9 and 10, for which the zero datum in the same figures represents the mean surface at the time of Geosat ALW 1987 (not Seasat ALW 1978). These continental ice-sheet results were then adjusted using the sea-ice results for Geosat ALW 1987 crossed with ERS-1 ALW 1992 and 1993 (table 3), respectively, where both of the latter analyses were carried out using retracked sea-ice data.
Using slope-corrected data over the continental ice sheet, the result obtained for ALWs Geosat 1987 crossed with ERS-1 1992 is: (-0.015 ±0.107) - (0.514 ± 0.014) = 0.529 ± 0.108 m. That is, the adjusted mean elevation rate is -106 ±22 mm a−1 over the 5 year time interval. For ALWs Geosat 1987 crossed with ERS-1 1993, the result obtained using slope-corrected data is: (0.112 ±0.135) - (0.553±0.015) = -0.665 ±0.136 m. That is, the adjusted mean elevation rate is -111 ±23 mm a−1 over the 6 year time interval (surface lowering in both cases).
Using data not slope-corrected over the continental ice sheet, the result obtained for ALWs Geosat 1987 crossed with ERS-1 1992 is: (0.431 ±0.023) - (0.514 ± 0.014) = -0.083 ±0.027 m. That is, the adjusted mean elevation rate is -17±5 mm a−1 over the 5 year time interval. For ALWs Geosat 1987 crossed with ERS-11993, the result obtained using data not slope-corrected is: (0.287 ±0.033) - (0.553 ± 0.015) = -0.266 ± 0.036 m. That is, the adjusted mean elevation rate is -44±6 mm a−1 over the 6 year time interval (surface lowering in both cases). These results for the mean rates-of-change of the surface heights, obtained using all-retracked sea-ice data (Geosat to ERS-1) to adjust the results obtained using retracked data over the continental ice sheet (Geosat to ERS-1) appear as the last two lines in Table 4
9. Comparison of adjusted results to other work
An estimate of the mass balance of the Wilkes Land sector of EAIS was made by Reference YoungYoung (1979), using oversnow traverse data. He concluded the sector was approximately in mass balance. (See also Reference Budd and YoungBudd and Young, 1979; Reference Raynaud, Lorius, Buddand and YoungRaynaud and others, 1979.) This conclusion was based on the uncertainty range for the measured surface velocities, expressed as mean velocities through the ice depth, which overlapped the uncertainty range for the balance velocities derived from accumulation measurements over the up-glacicr catchment areas. Young (1979) did not express his results in terms of an uncertainty range for the rate of thickening (thinning) of the up-glacicr catchment areas, but it is possible to do so by using the velocity error ranges from his table I, his stated uncertainty of ±20% for the accumulation data, and the catchment-basin areas (assumed to have negligible error) from his table II, and by assuming that the measured ice thicknesses in his figure 5, which vary around 3000 m and for which no error range is given, have an uncertainty of roughly ±20 m (personal communication from M. Nolan, 1997). Using a “box model” for the snow catchment area, with mass input from accumulation over the top surface of the box and mass dis-charge through the traverse line which constitutes the downstream face of the box, and propagating the errors, suggests that mean rates-of-change of the surface height upstream from the traverse line with in the range +90 to -90 mm a−1, approximately, would be consistent with Young's (1979) conclusion that the Wilkes Land sector is in mass balance. The catchment areas for Youngs study are south of 72.1° S (i.e. outside the altimetry measurement area shown in Figure 1), but it is worth noting that the adjusted rates-ol-change of the surface height shown in Table 4(except for the “slope-corrected” case, last two lines) are all well within our inferred uncertainty range, corresponding to Young's (1979) conclusion that the Wilkes Land sector is in mass balance.
The rates-of-change of the surface height estimated from altimetry for the region north of 72.1'' S and above the 1500 m elevation contour can also be compared to evidence from ice cores for accumulation changes during recent decades, and to numerical modeling results indicating the probable effect of these accumulation changes, if they have been widespread, on the time rate-of-change of the snow surface.
Evidence from widely spaced EAIS ice cores suggests that accumulation rates have increased during the decades since 1955—65 (personal communication from E. Mosley-Thompson, 1997). Pourchet and others (1983) found that at Dome C, precipitation increased by 30% after 1965 compared with 1955-65. Reference Morgan, Goodwin, Etheridge and WookeyMorgan and others (1991) found an increase in accumulation rates following a minimum around 1960, leading to recent rates about 20% above the long-term mean in the Wilkes Land sector of EAIS. Two of their cores, showing 23% and 26% accumulation increases, respectively, were located north of 72° S. Reference Mosley-ThompsonMosley-Thompson and others (1995) found that the accumulation rates at South Pole station have increased by about 30% since 1955. More recent data (personal communication from E. Mosley-Thompson, 1997) indicate that the increase was about 18-19%, on average, between 1955-64 and 1965-95. Unpublished data from a suite of shallow cores obtained at a remote site on the EAIS plateau, at 84° S, 43° Ε (elevation 3300 m), indicate that accumulation rates there have increased by about 23% during the past 150 years (personal communication from E. Mosley-Thompson 1997).
The time rate-of-change of the surface height at a given location on an ice sheet is given by the surface kinematic equation, which is a function of the accumulation rate, the vertical velocity and terms representing the rate of advection of higher-elevation ice from up-glacicr (e.g. Reference HutterHutter, 1983, p. 45.3). Lingle and Troshina (1998) show, using a time-dependent three-dimensional numerical model, that the positive change in the time rate-of-change of the surface height on the (non-equilibrium) EAIS north of 72° S, caused by a linearly increasing accumulation rate, is essentially equal to the lacrease in accumulation rate over time periods as short as 20-40 years after the start of the increase. Using the South Pole station value for the near-surface density of snow (360 kg m ' ; Mosley-Thompson and others, 1995), and the mean value of the accumulation rate with in the measurement area of this study (0.22 mm a−1 of ice, calculated by Lingle and Troshina (1998) using gridded accumulation data from Reference DrewryDrewry (1983)), and using the 23-26% increase in the accumulation rate from 1955-65 to 1975-85, measured by Morgan and others (1991) in their cores GD03 and GD15 as representative of the change north of 72° S (1, the implied positive change in the rate-of-change of the surface height is about 110 mm a (snow equivalent).
This modeling result should be viewed as a maximum, because increased rates of accumulation over the ice sheet would also result in increased rates of snow compaction. Given that, however, this result is clearly much greater than the rates of change inferred here from altimetry (table 4). This, in turn, leads us to speculate that the accumulation increases during recent decades measured in EAIS ice cores may have been counterbalanced somewhat by disequilibrium, or may not have been widespread throughout the measurement region shown in 1ur or, alternatively, that the increases may not have been typical of the relatively-recent 1978-93 time-frame considered here.
10. Discussion
The problem of using satellite altimetry to estimate mean changes of elevation on an ice sheet over time periods longer than the lifetime of one satellite is closely tied to the problem of estimating intersatellile radial bias over the measurement region, where “intersatellite radial bias”, as noted above, is defined as the sum of intersatellite orbit bias, instrumental bias and other sources of error causing different altimeters to yield systematically differing measurements of the same surface. We address that problem for the measurement region over the EAIS north of 72.1° S (1 by using the offshore ALW sea ice (11 as a reference surface. As also noted above, however (in section 7), sea ice can be less than ideal for that purpose. in this section we discuss some of the uncertainties associated with this procedure, and some additional sources of uncertainty associated with satellite measurement of small changes in surface elevation on the EAIS.
The potential error introduced by using non-retrackeel Seasal sea-ice altimetry in conjunction with retracked Geosat and ERS-1 sea-ice altimetry was investigated by independently using retracked Geosat and retracked ERS-1 sea-ice altimetry to estimate the intersatellite radial bias between those two satellites (table 3). This was then used to adjust the results obtained over the continental ice sheet between Geosat and ERS-1, using retracked altimetry between the same two sets of years. The results over the continental ice sheet, not adjusted using the sea-ice results, are shown by the points inside the clashed boxes in figures 9 and 10. These can be seen to be qualitatively similar to the results of Seasat crossed with ERS-1, although the apparent elevation increase is less (relative to the datum, representing in this case the Geosat surface), which is apparently due to the lesser radial bias between Geosat and ERS-1. When the Geosat x ERS-1 results are adjusted using the retracked sea-ice crossover results between the same two satellites, the results are also qualitatively similar to the adjusted Seasat x ERS-1 results (see last two lines in Table 4). However, in the case of the relatively noisy slope-corrected continental ice-sheet data, the Geosat to ERS-1 elevation rate is substantially more negative (about - 111 mm a−1) than any of the other cases (table 4), leading to suspicion that this result is less reliable than the results obtained using data not corrected for slope-induced errors. This suspicion is due to the slope corrections being derived by gridding the non-slope-corrected altimetry, then computing the slope corrections, then rcgridding the slope-corrected elevations after the first iteration, etc., in a method of successive improvements (see Brenner and others, 1983) which also has the effect of propagating the gridding errors back on to the elevation measurements. This outcome is reflected in the larger error bars for the slope-corrected crossover results shown in Figure 9, relative to the error bars in Figure 10.
An additional (potential) source of error in sea-ice altimetry could be outliers caused by, for instance, snagging on leads. Outliers from this and other causes are effectively eliminated, however, by the iterative 3σ edit. 8ur shows that the distribution of edited sea-ice crossover differences is similar to (although slightly less symmetrical than) the edited distribution of continental ice-sheet crossover differences (figs 4 and 7), even though the Seasal sea-ice data were not retracked.
Whether inlersatellite radial bias over a given measurement region (the ice sheet) can be estimated using a reference surface located somewhere else (the sea ice) is more of an open question. Although instrumental bias can be considered a constant function of position, geographically correlated intersatcllite orbit bias must be assumed to vary gradually in a spatial sense. The longitudinal component of this variation would be averaged similarly over the sea ice and ice sheet, but if this variation also has a latitudinal component, an error may be introduced by applying the sea-ice estimated bias to the continental ice-sheet altimetry. This error, if it exists, is noi taken into account.
Mean changes in the surface height, when computed on a same-season basis, are also subject to interannual variability. figures 9 and 10 show, for example, that when the Seasat altimetry of ALW 1978 was crossed with the subsequent ALW seasons of Geosat, the apparent change and rate-of-change of the surface height was not uniform, and ALW 1985, in particular, appears as an outlier with respect to ALWs 1986-88 (10. Interannual variability is also present in the Seasat to ERS-1 results, and if the outlier seasons that were eliminated from figures 9 and 10 (seetables 1 and 2) are included, the apparent seasonal variability is greater still. We have attempted to minimize the random component of the interannual variability by choosing ALW seasons having consistent crossover results for 2-3 years (for Seasat x Geosat, then Seasat x ERS-1) for computation of the elevation rates shown in Table 4
The altimetry-derived mean changes in surface height throughout the region shown in 1ur may, in addition, have a contribution due to isostatic uplift caused, in turn, by retreat and thinning of the Antarctic ice sheet since the Last Glaciol Maximum (LGM) about 20 000 years ago. A maximum estimate of the magnitude of this contribution can be made by noting that elsewhere, beneath the central Ross Ice Shelf in West Antarctica where much greater retreat has occurred since the LGM, Lingle and Clark (1979) predicted that the present rate of relative sea-level fall (mostly isostatic uplift) is likely to be about 12 mm a−1. Near the present grounding lines of the West Antarctic ice streams entering the Ross Ice Shelf, the present rate of isostatic uplift was predicted to be about 25 mm a−1 by Reference Greischar and BentleyGreischar and Bentley (1980), and about 15 mm a−1 by Lingle and Clark (1985). The rates of isostatic uplift around the coast of East Antarctica (1 are likely to be less, because the retreat distance from the edge of the continental shelf there is substantially less than retreat through the Ross Sea in West Antarctica, and the associated ice unloading would have been correspondingly less (although the Amery Ice Shelf area may be an exception). in any case, altimetry-derived elevation rates of the order of 10 mm a−1, comparable to the maximum positive rates in Table 4, may have a substantial contribution from isostatic uplift. Negative elevation rates, such as the minimum values in Table 4, are less likely to have a substantial isostatic component if thinning and retreat since the LGM have not been reversed during recent centuries.
11. Summary
Mean changes of surface height on the EAIS have been estimated during the 13 year time period between Seasat (ALW, 10 July-9 October 1978), and the corresponding ALW seasons of the Geosat GM (1986), the Geosat ERM (1987,1988), and ERS-1 (1991-93), using the method of orbit crossover analysis. Altimeter-derived surface heights corrected for slope-induced errors were used, and surface heights not corrected for slope-induced errors were also used for comparison. The data were corrected for atmospheric and ionospheric effects, solid-earth tides and, over the sea ice, ocean tides. Errors due to high noise levels in the data were minimized using the data and crossover selection procedures described above, and by averaging the crossover differences throughout the entire region north of 72.1−1S and above 1500 m elevation (1. Errors caused by the nature oHhe retracking method were minimized by using altimetry from all three satellites retracked using the same technique (GSFC version 4). Errors due to systematic ascending-descending bias among the orbits of the same satellite (intrasatellite orbit bias) were cancelled in the averaging procedure. The systematic biases between different satellites, including orbit bias and other sources of systematic radial error such as instrumental bias, were estimated using crossover differences on the ALW sea ice (employed as a gcoid-parallel reference surface), and were used to adjust the intersatellite elevation changes estimated on the continental ice sheet. The altimeter-derived surface heights from all three satellites are referenced to JGM-2 orbits and the WGS84 ellipsoid.
The numerical results, which are summarized below in terms of ranges of values, represent the total range from the lowest value less 3σ to the highest value plus 3σ of the mean (seeTable 4). The additional random errors associated with the corrections for intersatellite radial bias are included in these uncertainty ranges.
Between ALW 1978 of Seasat and ALWs 1987 and 1988 of Geosat, the estimated mean rate-of-change of the surface height, computed using slope-corrected altimetry, was -4 to +11 mm a−1.The ratc-of-change of the surface height estimated using non-slope-corrected altimetry between Seasat and ALWs 1986-88 of Geosat was 11 to +11 mm a−1, where the minus value implies decreasing surface height.
Between Seasat and ALWs 1991-93 of ERS-1 the mean rate-of-change of the surface height, computed using slope-corrected altimetry and a minimum estimate of Seasal to ERS-1 radial bias, was 40 to - 15 mm a . Using non-slopc-corrected altimelry and the minimum bias estimate, it was -22 to Omm a−1.
Between Seasat and ALWs 1991-93 of ERS-1, the mean rate-of-change of the surface height, computed using slopc-corrected altimetry and a maximum estimate of Seasat to ERS-1 radial bias, was 55 to 33 mm a−1. Using non-slopc-corrected altimetry and the maximum bias estimate, it was -36 to-17 mm a−1.
Finally, the Seasat to ERS-1 results were checked for consistency by computing the mean rate-of-change of the surface height between ALWs 1987 of Geosat and 1992 and 1993 of ERS-1, and similarly adjusting the results for inter-satellite radial bias estimated using sea-ice crossover differences computed on a same-season basis between the same sets of years. LIsing slope-corrected altimetry over the continental ice sheet, the adjusted mean rate-of-change of the surface height was 130 to 84 mm a~−1. Using altimetry not corrected for slope-induced errors over the continental ice sheet, the mean rate-of-change of the surface height was -50 to -12 mm a−1. The latter result is consistent with the Seasal to ERS-1 elevation rates (table 4). The former result may be less reliable, because the slope-corrected Geosat 1987 to ERS-1 1992 and 1993 crossover differences are relatively noisy (note the 3rr error limits in Table 4).
The mean rate-of-change of the surface height estimated using all crossover analyses between Seasat and Geosat (ALW 1978 to ALW 1986-88) was thus with in the range -11 to + llmma~', which is not significantly different from zero. Between Seasat and ERS-1 (ALW 1978 to ALW 1991-93), the mean rate-of-change of the surface height estimated using all crossover analyses (but excluding the slope-corrected cases, last two lines of Table 4) was with in the range -55 to 0 mm a−1, which suggests that the surface may have lowered, on average, during this time interval. The inconsistency of the bias-adjusted Seasat to Geosat vs Seasal to ERS-1 results may be an expression of interannual variability, or an indication that orbits more accurate thanJGM-2 are needed for measurement of regional multi-year mean changes of elevation on the EAIS. Alternatively, it may be a reflection of the differing orbit inclinations of Seasat and ERS-1.
Acknowledgements
We thank the NASA Polar Research Program for supporting this work with grant NAGW-4371 to C Lingle; the Cray Research, Inc., University Research and Development Grant Program for additional financial support; the European Space Agency for acquiring ERS-1 Antarctic altimelry; and the Arctic Region Supercomputing Center for computational support. We also thank J. Zwally, A. Brenner, J. Dimarzio and B. Legcer for providing the v.4 and earlier level 2 altimeter data used in this study, for information regarding the tapes, and useful comments and conversations; E. Troshina for modeling computations; E. Mosley-Thompson for providing accumulation data and related information from her East Antarctic ice-core studies; K. Partington for useful conversations; and J. Ridlev and an anonymous reviewer for comments that improved the manuscript.

















