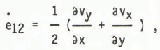1. Introduction
Strain-rate measurements on a firn pit 20 m deep were made to gain a better insight on the movement of the firn of a temperate glacier. The firn pit originally had a depth of 20 m, a diameter of 2 m and an approximately circular cross-section. At 14 levels of different depths 6 or 7 gauges on each level were set in the pit walls, which were measured once a year in July between 1967 and 1978. Yearly-averaged strain-rates are obtained, no seasonal variations being taken into account. Greater details on the measurement and analysis of the strain-rates are given in Eisner and Ambach (1981).
The stratigraphy and the density profile at the site of the measurements were taken from studies on an analogous firn pit in the immediate neighbourhood (Ambach and Eisner 1966). The firn pit lies in the central region of the accumulation area, the slope of the surface being approximately 5°. The averaged water equivalent of the annual net accumulation for the period from 1967 to 1980 amounts to 1.3 m. The transition zone of firn into glacier ice lies approximately 25 to 28 m deep (Behrens and others 1979). Meltwater percolation through the firn occurs during midsummer in warm periods. The site of the measurements cannot be claimed as a neutral zone in relation to the state of stress.
It is the aim of the present paper to give new information on the rheological properties of the firn of a temperate glacier from strain-rate measurements on a firn pit. Field experiments of this kind are better than laboratory experiments as the firn and ice structure and the stress correspond to conditions in nature.
2. Strain-Rates
The following deformation effects have become evident (Eisner and Ambach 1981).
-
(a) The creep profile obtained by the measured shear strain can be approximated by a straight line. The velocity gradient is thus approximately constant and independent of the depth. From the linear creep profile and the shear stress the effective shear viscosity can be calculated as a function of depth.
-
(b) The deformation of an approximately circular cross-section into an elliptical one is marked by the hexagonally arranged gauges. Changes of the measured strain-rates with time cannot be confirmed clearly, and no statements on the effects of secondary and tertiary creep can be made.
-
(c) Progressive immersion of the levels into the firn takes place, due to the vertical component of movement, which is generated by both the settlement of the snow by compression and the thinning of the snow layers by the tensile stress occurring in the accumulation area of glaciers. This tensile stress is related to the increase of the velocity in the direction of the flow.
All strain-rates were calculated as averaged strain-rates over the period of measurements. Therefore, no time dependence of the strain-rates can be taken into account. The linear creep profile in the firn of a temperate glacier shows a shear deformation similar to that of the well-settled snow pack (Reference McClungMcClung 1980) and differs significantly from parabolic creep profiles obtained in incompressible glacier ice (Savage and Paterson 1963).
3. Effective Shear Viscosity and Effective Bulk Viscosity
For determining the shear viscosity and the bulk viscosity of firn, a stress strain-rate relation must be derived. As the firn is a compressible medium having a multi-axial state of stress with superimposed shear stress, the problem can be solved in terms of invariants. Great efforts have been made to create a constitutive Equation describing the Theological behaviour of snow in general (Salm 198Z). However, for practical application, a simplified model is needed to reflect the predominant properties of the firn.
3.1. Constitutive Equation
The stress tensor and the strain-rate tensor can be written in the form
and
where σij eij are the components, σij eij are the deviators σijare the first invariants and δij eij is the Kronecker symbol. The shear viscosity u and the bulk viscosity n are introduced by definition as follows:
and
Therefore it holds that
and
Introducing the parameter k by
the constitutive Equation (7) can be rewritten
and the ratio n/u becomes by comparison of Equation (3) and Equation (4)
The parameter k is a quantity depending mainly on the compressibility of the firn, with k = 1, when the material is noncompressible. k is related to the viscose analogical form of the Poisson’s elastic ratio v, which is defined for an uniaxial state of stress by
From Equation (9) it holds with σ11=I1

and by comparison of Equations (11) and (12) results in
The quantity k, the shear viscosity μ and the bulk viscosity n depend on density and on other structural parameters and/or on stress invariants (Reference SalmSalm 1977). As the dependence of the shear and bulk viscosity from the state of stress is unknown in this experiment, numerical values are introduced as effective viscosities which are only valid for the state of stress under investigation. The idea behind this approach is that the field experiment indicates natural conditions which are difficult to reproduce in laboratory tests.
3.2. Results
The following quantities are known from the field experiment: the strain-rates ė11, ė22, ė33, ė12 and the stresses α22, α12. Index 1 denotes the direction of the flow, 2 the direction of depth, and 3 the direction transverse to the flow.
The evaluation was made by the following steps:
-
(a) Calculation of the shear viscosity >i as a function of depth, obtained from the creep profile and the shear stress (table 1) by
with(14) and(15)
and(15) where ρ is the density, g the gravity, a the slope and vx, Vy are the components of the velocity in the direction of the flow and the direction of the depth. It follows from velocity measurements on the glacier surface that the term ρ Vy/ ρ × can be neglected (Schneider unpublished).(16)
where ρ is the density, g the gravity, a the slope and vx, Vy are the components of the velocity in the direction of the flow and the direction of the depth. It follows from velocity measurements on the glacier surface that the term ρ Vy/ ρ × can be neglected (Schneider unpublished).(16)
-
(b) Calculation of the quantity k as a function of depth from Equation (13). The ratio v, being by definition reciprocal to the cross-section number, is given as a function of density by Bader and others (1951). Any dependence of k from the state of stresses is neglected, as the state of stresses is unknown.
-
(c) Calculation of the bulk viscosity q as a function of depth by
using the shear viscosity u and the quantity k as a function of depth (Table I).

Fig. 1. Axial viscosity of firn of a temperate glacier (1) calculated from the effective shear and effective bulk viscosities of the present paper by nE = 9(μeeff neff)/(3neff + μeff) (Reference MellorMellor 1975). Comparison of axial viscosities of different snow types (A to E) after Mel lor (1975). Data of the present analysis (1) are temperature: summer 0°C, winter -10°C (estimated); stresses: shear stress -7.74 to -16,65xl03 Pa; vertical axial snow load -87 to -185xl03 Pa; μeff and neff see Table I.
Table 1. Shear Strain-Rate ė12, Shear Stress α12, Axial Snow Load α22, Effective Shear Viscosity μ And Effective Bulk Viscosity N, Of Firn In Dependence Of Depth, Density And Cross-Section Number

Both the effective shear viscosity and the effective bulk viscosity increase with depth, partly due to increasing density and incompressibil ity and partly due to increasing normal stress in agreement with results obtained for a well-settled snowpack (McClung unpublished). The results fit very well into a graph showing the viscosity as a function of density for different types of snow (Fig.l).
In the present analysis, it is a hypothesis that snow is an Isotropie medium and that the stress deviator tensor is linearly proportional to the strain-rate deviator tensor, the constant of proportionality being independent of speed and memory effect.
Conclusions
The following critical considerations must be taken into account. Firstly, the shear viscosity y and the bulk viscosity n depend strongly on temperature, structure and state of stresses. The numerical result must therefore be understood in terms of effective shear viscosity and effective bulk viscosity. It is not possible to determine the viscosity function as introduced by Reference Salm and OuraSalm (1967). Secondly, the firn is an anisotropic material because of its horizontal stratification. However, the Equations used in this paper are those for an isotropic material. Therefore the effective shear viscosity determined from the shear stresses may differ from that determined from axial stresses. Thirdly, the calculated effective viscosities are mean values valid for each individual level. It must be considered that significant changes in depth, density and stresses occur for each level during the period of measurements. However, the influence of temperature is of less importance, as the firn pit was dug in a temperate glacier.
Acknowledgements
The project was assisted with the financial support of the Osterreichische Akademie der Wissenschaften, Vienna. Transport was supplied by the Bundesministerium für Inneres, Vienna. The authors express their thanks to Dr H Jessberger, Dr D McClung, Dr C Raymond and Dr B Salm for making comments on the problem and to Mr K Kimeswenger for cooperating in the evaluation. The more detailed manuscript will be submitted to Zeitschrift für Gletscherkunde und Glazialgeologie