INTRODUCTION
Since 1967 snow storage in Norway has been estimated by the gamma-ray spectrometer method (Figure 1), based on systematic measurements of natural gamma-rays detected from aircraft (Dahl and 0degaard 1970). After a test period from 1967 to 1972 to obtain a satisfactory routine, the method has been applied since 1973 for operational measurements in a number of basins in southern Norway. Measurements are undertaken twice each winter in nine high mountain basins. The fiightlines total about 1 000 km.

Fig. 1. Principle of measuring the snow water equivalent (SWE) by the gamma method.
The “total count” method is used. The terrestrial gamma radiation will mainly be emitted from potassium-40, bismuth-214 and thallium-208. Thus the net count rate in the energy-interval 0.05-3.00 MeV is detected. The average flight altitude is 150 m above the ground. Navigation is visual from maps (I: 50 000). The snow water equivalent (SWE) normally ranges between 250 and 700 mm. The greatest amount of snow accumulates in basins near the west coast. Measurements of natural gamma radiation from the ground are taken along the fiightlines in autumn before snowfall and in winter,
These surveys are organized by the Norwegian State Power System as a part of their efforts to determine the available water resources for their water reservoirs. Data from ten years of measurements have been studied to evaluate the method and give guidelines for improvements in operational routines. This work is reported by Andersen and Johnsrud (1984).
As wind drift causes redistribution of the snowpack, snow distribution is uneven in high mountain basins. Physiographic factors such as topography and vegetation, as well as the main direction of the wind, play an important role in how the snowpack is redistributed.
A simple computer model is developed to study the influence of different snow distributions and various sizes of snowfree area to the results from the gamma method.
BASIS OF METHOD
Snow cover attenuates the gamma radiation from the ground. From well-known principles in radiation theory, the water equivalent of the snowcover (SWE) can be calculated (Kogan and others 1971):

where J = intensity of gamma field, N = number of energy levels, q = volume source density, μs, μw and μa are respectively linear absorption coefficients of surface, “water and air, Ea = exponential integral of second kind, B = build-up factor, A ·= altitude, and W = snow water equivalent.
For snowcovers thicker than 100 mm, water equivalent Equation 1 could be adequately approximated by an empirical relation (Dahl and Ødegaard 1970).
No= net count rate without snow, N8 = net count rate with snow.
a and b are constants

For calibration of a and b the direct ground measurements of the snow were carried out simultaneously to the gamma-ray surveys. Inserting Equation 3 into Equation 2, we obtain the equation used for operational measurements in Norway.
DESCRIPTION OF THE MODEL
The model may calculate the intensity of the radiation field from the surface for various snow distributions. Equa-tion 1 between SWE and gamma radiation is non-linear. Sharp decrease in gamma ray count corresponds to an increase in SWE. Unevenness of snow cover and the presence of snow-free areas are thus clearly indicated in the results of the survey (Cork and Loijens 1980).
A detector placed in an aircraft will “see” the surface as a disc (Figure 2), which is divided into small elements. The area of each element and the distance from the detector is easily calculated. The gamma radiation intensity △Ji from one element with the area △S can be calculated by:

δ = areal source density, element to the detector and ra = distance from the

Fig. 2. Principle of the method used to divide the disc into small elements.

The intensity from the whole disc is calculated by:

K is the number of elements in the disc μa and μw are regarded as constants through the absorbing media. It is now possible to “put” all kinds of snow distributions on the disc, by giving each element a fixed SWE.
USE OF THE MODEL
The effective radiation area
Measuring the radiation intensity at a given point, the gamma-rays from the areas closest to the detector have the highest possibility of reaching the detector. The area from which 90% of the radiation is emitted is called “the effective radiation area” (Aeff). At an altitude of 150 m above the surface Aeffis 0.32 km2, when μa= 0.0082 m1 and μw = 6.3 m1. The radius of this area is about 320 m, approximately twice the flight altitude. The calculations are made without snow on the ground and the areal source density is taken to be uniform.
Even snow distribution
In lowlands below the tree limit (1 000m a.s.l.) variations of snow cover are different from those in high mountains. The coefficient of variation is typically 0.1-0.2 (Gottschalk and Jutman 1979). As a basis for comparing various uneven snow distributions, the intensity of the gamma radiation field from an even snow cover is calculated.
The transmission quotient expressed in per cent, T, is defined as follows:

where J o and J 8 are the calculated intensity respectively with and without snow on the ground.
Figure 3 (curve 1) shows how T acts as a function of SWE with an even snow cover. With T = 50% SWE is 72 mm. when SWE exceeds 265 mm then T is less than 10%.
Uneven snow distributions
Snowdrifts together with physiography cause uneven snow distribution, particularly above the tree limit. The snow concentrates at places with relatively low winds, eg along leeward slopes and in valleys, hollows and river beds; this results in a strong redistribution of the snowpack. In
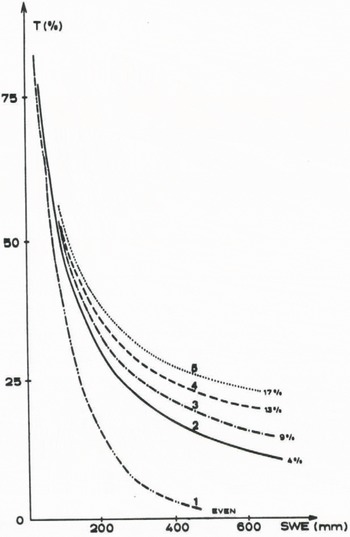
Fig. 3. Graphs from model calculations with various snowfree areas in the snow distribution. 1: even snow distribution, 2: Nea distribution 4% snowfree, 3: Nea distribution 9% snowrree, 4: Nea distribution 13% snowfree, 5: Nea distribution 17% snowfree.
Norway only a few attempts have been made to map snow distribution in high mountain areas.
For calculations with the model a snow distribution curve from the basin Nea (a high mountain area, see Figure 4) based on snow courses measured on the ground is used (Killingtveit og Aam 1978). The snow distribution is digitized in the model in a way that makes SWE vary both radially and circularly on the disc. 4% of the area is set snowfree in these conditions.
When the snow storage increases, the gamma radiation decreases rapidly. With an average SWE on the disc equal to 94 mm, the intensity in the gamma radiation is reduced to 50% (Figure 3). When SWE reaches 260 mm the gamma radiation intensity from the surface is decreased to 25%.
Variation in the unevenness of snow distribution
Meteorological conditions vary through the winter and from year to year. Main wind direction and the amount of snow are important for the actual snow distribution. Figure 5 shows the snow distributions along a snow course at West Hardangervidda in 1982, 1983 and 1984.
To show the importance of such variations for the gamma method the gamma intensity of three different snow distributions are calculated in the model. The snowfree area is fixed, 4%. Figure 6 illustrates the calculated T as a function of SWE. Note the difference between the Nea distribution (solid line) and the most uneven snow distribution (dashed line). When T = 29% the difference in SWE between the two snow distributions is 100 mm. When T - 20% the difference is 175 mm.
Variation of the snowfree area
When the measurements are taken, melting may have removed the snow from some local areas in the basin. With

Fig. 4. Snow distribution curves used in the model calculations. 1: extreme uneven snow distribution (constructed), 2: Nea distribution (measured along snow courses on the ground), 3: constructed medium uneven snow distribution.
the snow distribution from Nea as a basis, the snowfree area will increase as a function of the snow melting. If the gamma method is used to assess the snow storage during the melt period, the size of the snowfree area must be taken into account.
In the model calculations the snowfree area has been increased by removing the lower part of the Nea distribution. Figure 3 shows the graphs from the calculations with different snowfree areas with curves for 9%, 13% and 17% of the disc snowfree in addition to Nea-distribution and even snow distribution.
As the storage of the snowpack increases, the graph moves asymptotic to a transmission per cent equal to the part of the snowfree area. The graphs (Figure 3) show how sensitive the gamma method is to variation in the snowfree area, especially with a high SWE.
DISCUSSION
In high mountain areas with little or no vegetation snow distribution is determined by weather conditions and topography. The unevenness of snow distribution has been taken into consideration in the most recent development of the gamma method in Norway. An empirical relation has been derived for the transmission as a function of directly measured snow storage.
Model calculations including variations of snow

Fig. 5. Snow distribution curves from three years along a course at west Hard anger vidda.

Fig. 6. Results of model calculations from the snow distributions in Figure 4. Graph 1 corresponds to curve 3 in Figure 4, Graph 2 to curve 2, and Graph 3 to curve
covered area show that when average SWE exceeds 250 mm only small variations in the snowfree area are decisive for the measurements. For reliable results it is essential to make gamma surveys before melting starts in areas with thin snow cover. The gamma radiation will be too high when large snow free areas are included, and snow storage will be underestimated.
With varying weather conditions the snow distribution will change from year to year. Model calculations with different snow distributions and constant average SWE will give diversities of T. In reality the snow distribution will not change to the same degree as on Figure 4. At most measurements in Norway, T is within the range of 20-30%. With great snow masses small variations in the snow distribution will cause considerably effect the measurements. If T deviates 1% from the empirical graph at 400 mm it will give an effect of 4% in the results. Corresponding for 600 mm the effect will be about 7%.
Measurements when SWE exceeds 500 mm must be considered unreliable. Knowledge of the snowfree part of the area would improve the surveys.








