Introduction
Cold, high-altitude Alpine glaciers which are located close to source regions of atmospheric pollution represent an important archive of climate history in central Europe. Ice cores have been drilled at four sites in recent decades, namely, on Colle Gnifetti and upper Grenzgletscher, Monte Rosa, Switzerland (Reference Oeschger, Schotterer, Stauffer, Haeberli and RothlisbergerOeschger and others, 1978; Reference Schotterer, Oeschger, Wagenbach and MunnichSchotterer and others, 1985; Reference Wagenbach, Munnich, Schotterer and OeschgerWagenbach and others, 1988; Reference Doscher, Gaggeler, Schotterer and SchwikowskiDoscher and others, 1996; Reference Schwikowski, Brutsch, Gaggeler and SchottererSchwikowski and others, 1999b), the Fiescher-horn, Switzerland (Reference Schwikowski, Doscher, Gaggeler and SchottererSchwikowski and others, 1999a), and Col du Dome, Mont Blanc, France (Reference De Angehs and GaudichetDe Angelis and Gaudichet, 1991; Reference Vincent, Vallon, Pinglot, Funk and ReynaudVincent and others, 1997).
Interpretation of the ice cores requires knowledge of the specific flow behavior of these small glaciers. Irregular surface and bed topographies lead to a complex three-dimensional flow field. Effects of firn compaction cannot be neglected since about one-third of the total glacier thickness consists of firn with densities below bubble close-off. Strong spatial and temporal variations of accumulation rates and surface temperatures further complicate the interpretation of the climatic record in these cores. Therefore ice-dating methods derived for polar sites (e.g. the model of Reference Dansgaard and JohnsenDansgaard and Johnsen, 1969) and flowline models are of limited suitability Knowledge of the full flow field is mandatory for determining the optimal location of a new drill site, for reliable constraints on the dating of ice cores and for a map of the source regions.
The Colle Gnifetti Drill Site
Colle Gnifetti is the uppermost part of the accumulation area of Grenzgletscher, forming a saddle between Zumsteinspitze and Punta Gnifetti of Monte Rosa, at 4400–4550 m a.s.l. The ice flows from both peaks to the main outflow of Grenzgletscher, or breaks off over a steep ice cliff on its northeastern margin (Fig. 1). The glacier is located between the recrystallization-infiltration zone and the cold infiltration zone (Reference Mean, Haeberli and SchadlerMean and others, 1984). Meltwater produced occasionally by intense solar radiation at elevated air temperatures refreezes some centimeters below the surface. Measured ice temperatures never exceed the range –9° to –14°G (Reference Mean, Haeberli and SchadlerMean and others, 1984; Reference Haeberli and FunkHaeberli and Funk, 1991; Reference LuthiLuthi, 1999). Measured accumulation rates are 0.2–1.1 ma–1 we with very strong spatial and temporal variations due to the wind exposed location of Colle Gnifetti (Reference Mean, Haeberli and SchadlerMean and others, 1984).
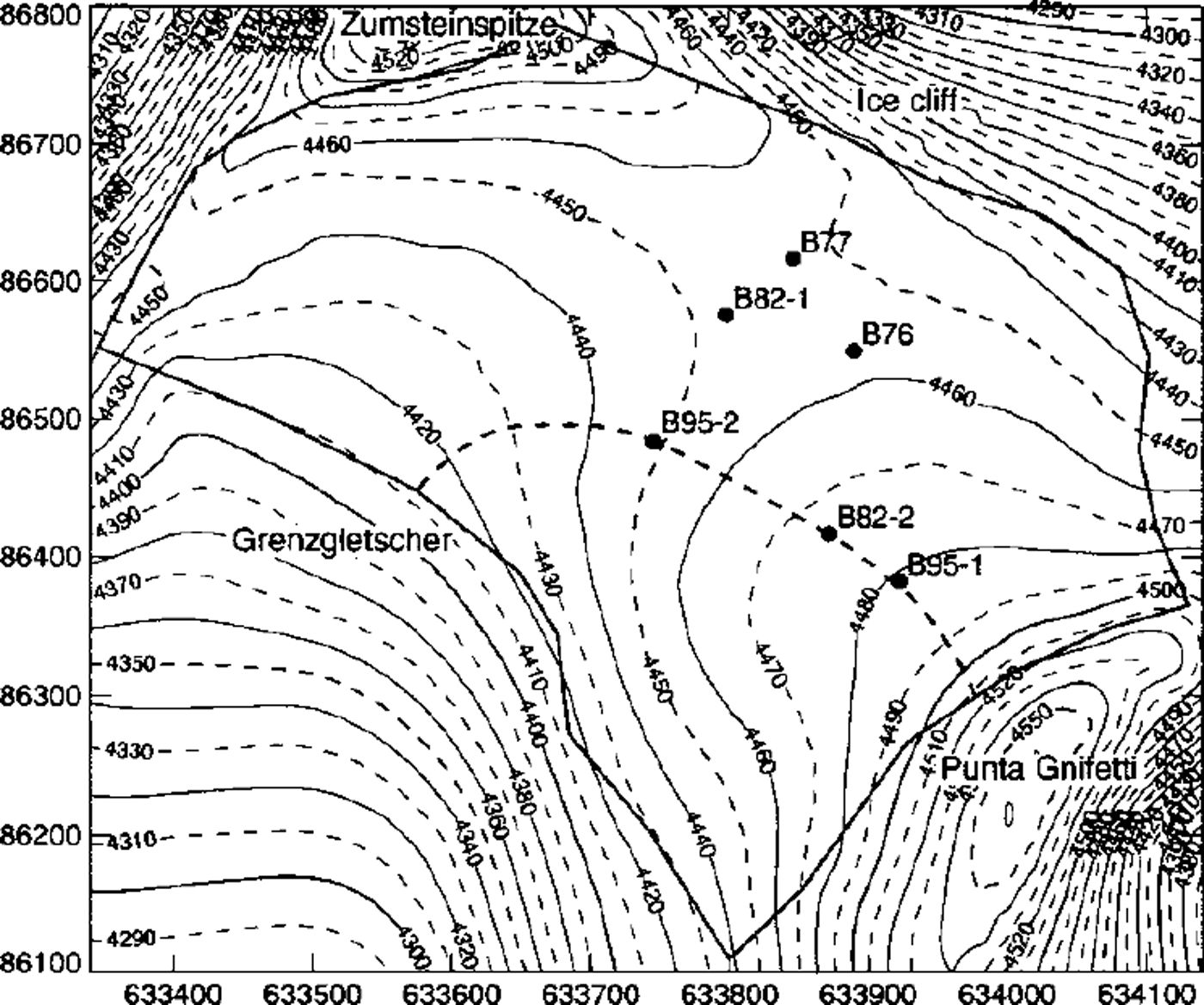
Fig. 1. Surface elevation map of Colle Gnifetti. The thick line indicates the border of the study area, and points mark the drill sites. Boreholes reached near bedrock at depths of 124m (B82–1), 66 m (B82–2), 61m (B95–1) and 101m (B95–2). Boreholes B76 (33m) and B77 (55 and 65 m) stopped far above bedrock. Coordinates are in meters and correspond to the official Swiss coordinate system; contour lines indicate the altitude above sea level. The location of the flowline model is marked with a thick dashed line.
These conditions conserve the accumulation history over a long time period. Consequently, Colle Gnifetti was one of the first glaciers in the Alps from which ice cores were investigated to obtain climatic information. Locations and designations of drill sites are shown in Figure 1. A first firn core was drilled to 33 m depth in summer 1976 (B76), followed by two cores from location B77 which reached depths of 55 and 65 m (Reference Oeschger, Schotterer, Stauffer, Haeberli and RothlisbergerOeschger and others, 1978; Reference Schotterer, Haeberli, Good, Oeschger and RothlisbergerSchotterer and others, 1981). Two drillings in 1982 stopped near bedrock at depths of 124 m (B82–1) and 66 m (B82–2) (Reference Schotterer, Oeschger, Wagenbach and MunnichSchotterer and others, 1985; Reference Wagenbach, Munnich, Schotterer and OeschgerWagenbach and others, 1988). In 1995, a new drilling program of the Universities of Heidelberg and Bern reached close to bedrock at depths of 61 m (B95–1) and 100 m (B95–2). These boreholes gave us the unique opportunity to perform in situ measurements of borehole closure and borehole inclination which allow conclusions to be drawn about the rheological properties of cold firn. A detailed description of the experiments is given below.
While the upper part of the ice cores has been dated back some 400 years by identifying well-known Sahara dust events and volcanic eruptions, the age of the lowest third is still undetermined (Reference Wagenbach, Geis, Leinen and SarntheinWagenbach and Geis, 1989; Reference Doscher, Gaggeler, Schotterer and SchwikowskiDoscher and others, 1996). Several observations lead to the conclusion that the ice is some thousands of years old, and some evidence supports the hypothesis that the lowest meters were deposited during the last ice age (e.g. Reference Wagenbach, Haeberli and StaufferWagenbach, 1994).
Flow models of increasing sophistication (Reference Haeberli, Schmid and WagenbachHaeberli and others, 1988; Reference WagnerWagner, 1996) were used to date the cores, and produced a good agreement with the chemically dated layers. Nevertheless they are not conclusive for the dating of the basal ice, predicting ages of 2000–15 000 years. This large time-span is due partly to uncertainties in bedrock topography and englacial temperatures, and mainly to the use of a mere velocity parameterization or neglect of the effects of firn compressibility.
Bedrock topography
Ice-thickness measurements performed in 1980 with single point radio-echo soundings resulted in a first bedrock topography map (Reference Haeberli, Schmid and WagenbachHaeberli and others, 1988). A total of 13 quasi-continuous high-frequency radar profiles were measured in 1989 and 1996 in collaboration with G. Meyer (Communication Technology Laboratory of ETH Zürich, Switzerland). Digital signal processing and seismic data-analysis methods (migration, resampling and static correction based on a density-dependent signal velocity model) allowed the ice thickness to be determined over a large part of the glacier to an accuracy of 4 m (Reference WagnerWagner, 1996; Reference LuthiLuthi, 1999). The maximum difference in the depths of boreholes reaching close to the bed is 2 m. The resulting ice-thickness map is shown in Figure 2, along with the location of the radar profiles. Ice thicknesses range from 60 m on the plateau below Punta Gnifetti to a valley 130 m deep in the central saddle area and towards the outflow into Grenzgletscher. The differences between the valley-shaped bedrock and the saddle-shaped surface lead to a complex ice-flow pattern in the glacier and especially in the vicinity of the saddle point between boreholes B77 and B82–1.
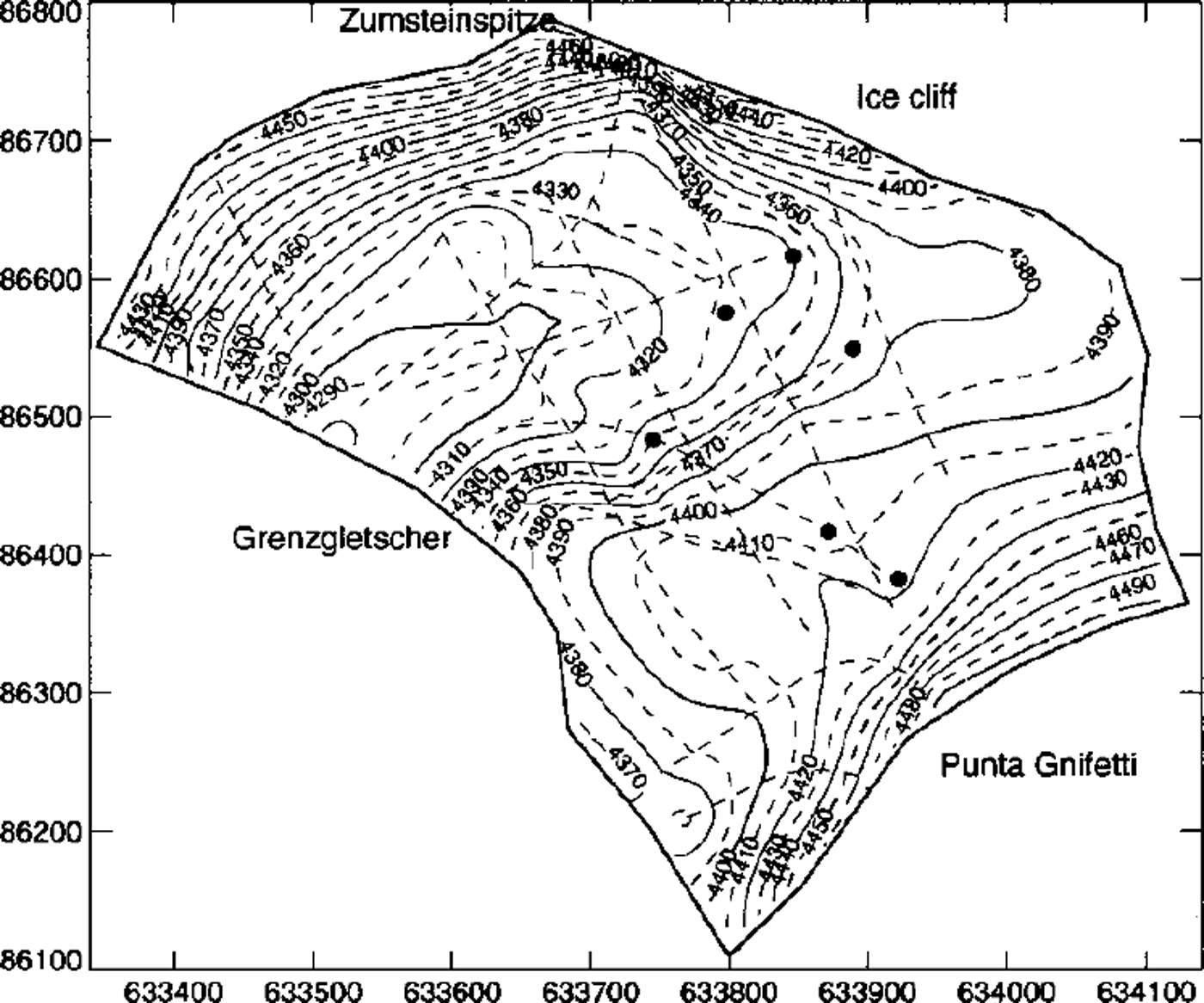
Fig. 2. Ice-thickness map of Colle Gnifetti based on radio-echo soundings indicated with dashed lines. The points mark the same drill sites indicated in Figure 1.
Borehole Experiments
Analysis of borehole closure and deformation is an important source of experimental evidence on the rheology of ice (e.g. Reference NyeNye, 1953; Reference PatersonPaterson, 1977). The closure of the 100 m deep borehole B95–2 drilled in 1995 was measured up to 431 days after completion of the drilling. Subsequently, tiltmeters and thermistors were installed in the borehole and frozen to the surrounding ice, which could be monitored for another year.
Borehole closure
The diameter of borehole B95–2 was measured with a three-leg caliper probe (manufactured by GEOCOM GmbH, Celle, Germany). The caliper was kept in the center of the borehole by the legs at the lower end and additional steel springs on the top. Only after the first measurements was it recognized that the electronic part of the caliper suffered from severe temperature-stability problems, as a result of which it was redesigned. Therefore, the initial borehole diameter is not known from measurements. We assume that it is only slightly enlarged by the drill passing up and down several times. The outer diameter of the drill was 104.8 mm (personal communication from H. Rufli, 1998), so the initial borehole diameter is assumed to be 106 mm.
The caliper was calibrated with seven plastic tubes at –15°C and at room temperature to an accuracy of ±0.3 mm. Recalibration in the field allowed eventual offset values to be determined which were accounted for in the data processing. The accuracy of the borehole-diameter measurements is about ±0.5 mm, and errors in the vertical position are ≤ 10 cm. The caliper was lifted with a hand winch, and instrument readings were recorded at 0.5 s intervals with a data logger, resulting in sampling intervals of 5–10 cm, depending on the fitness of the winch operator.
Due to the problems described above, only two of five field trips provided accurate borehole diameter logs. The borehole radius measured 140 and 431 days after completion of the drilling is shown in Figure 3. The measured radius exceeds the assumed initial radius in the uppermost 20 m, due at least partly to the strong forces exerted by the caliper legs on the firn. Since we have no means to infer the initial borehole radius, we assume a constant initial radius of 53 mm.
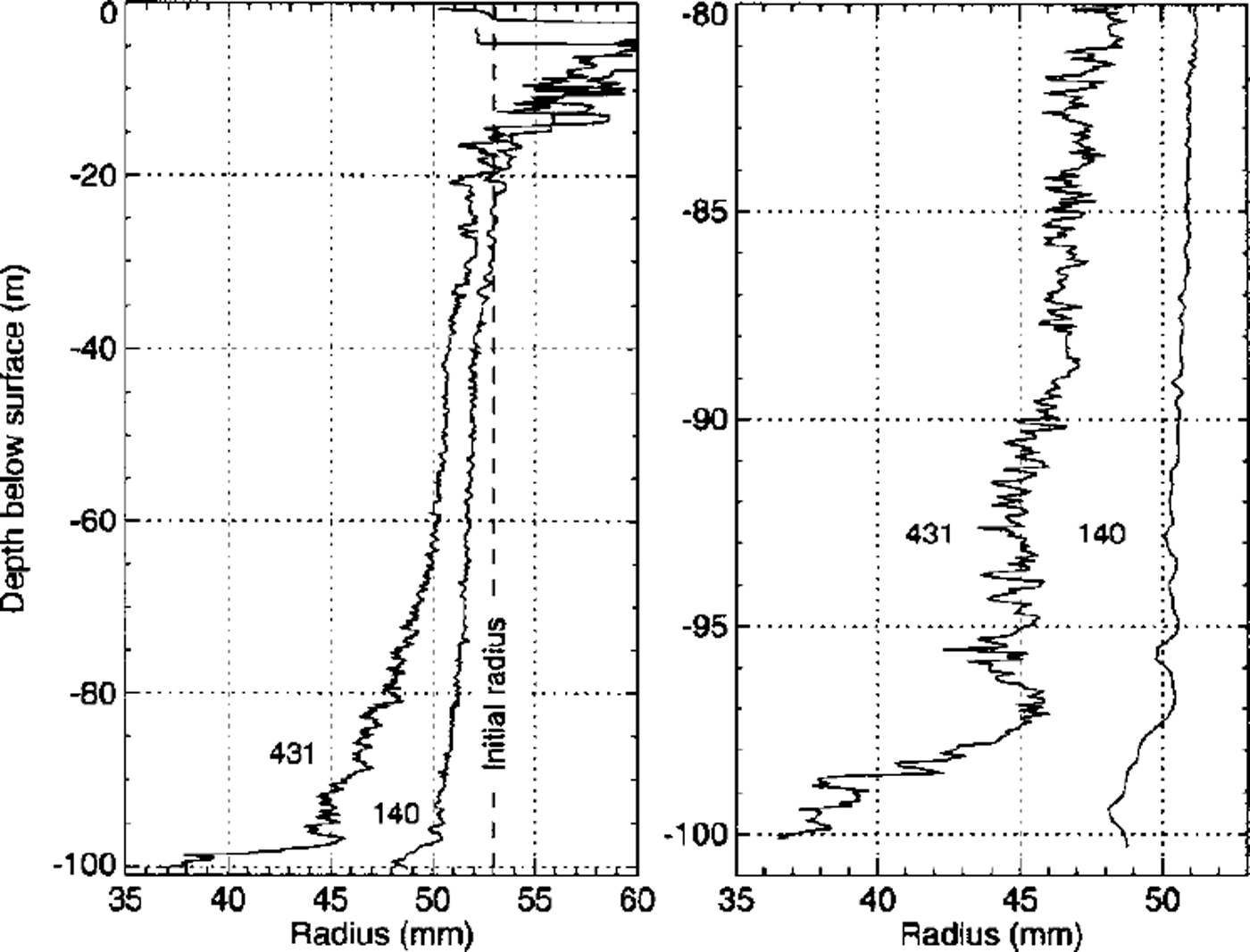
Fig. 3. Left: Radius of the 100 m deep borehole B95–2 measured 140 and 431 days after completion of the drilling The assumed initial radius is indicated with a vertical dashed line. Right: A close-up of the lowest part of the borehole where enhanced closure in the lowest 3 m is apparent.
The borehole shape (Fig. 3) exhibits some interesting features. Between 40 and 60 m depth the borehole radius does not vary substantially. This is an effect of the steadily increasing viscosity of the firn, counteracting the equally increasing compressive stress. Indeed, the bend at 40 m corresponds to the density of air-bubble close-off, which is about 815 kg m–3 at –13.5°C (Reference Martinerie, Lipenkov, Raynaud, Chappellaz, Barkov and LoriusMartinene and others, 1994). At this transition density, firn densification changes from the intermediate to the final stage (Reference DuvalDuval, 1985).
Anomalously fast borehole closure was observed in the lowest 3 m near bedrock, which is shown in an enlarged view in the right panel of Figure 3. An initially inclined borehole, which would lead to an apparently smaller borehole radius, can be ruled out as an explanation, since the shape of several features in the borehole-radius log evolves with time. This zone of enhanced closure is further discussed below.
Discussion
An analysis of the closure of an infinitely long cylindrical hole was developed by Reference NyeNye (1953) and was subsequently applied to the interpretation of borehole closure measurements (e.g. Reference PatersonPaterson, 1977). All physical quantities depend only on the radial coordinate τ if variations along the hole axis are neglected. The closure rate, measured at the borehole wall at distance R from the center, is defined by
![]() . Measurements R1 and R2
of the borehole radius at times t1 and t2
give an averaged closure rate over the time interval (Reference PatersonPaterson, 1977)
. Measurements R1 and R2
of the borehole radius at times t1 and t2
give an averaged closure rate over the time interval (Reference PatersonPaterson, 1977)

Closure rates calculated with this formula and an initial radius R0 of 53 mm are shown in Figure 4, together with measured density and temperature profiles. The borehole closure rate below 70 m depth did not change from the first to the second period, but varied considerably above. This and the negative closure rates in the uppermost 20 m stem, at least partially, from an inaccurate initial radius which is not known from measurements. Furthermore, measurement inaccuracies are introduced by the strong forces exerted by the caliper legs on the low-density firn above 20 m depth. For these reasons we confine our discussion mainly to the middle panel of Figure 4, showing closure rates calculated from the borehole radius after 140 and 431 days.
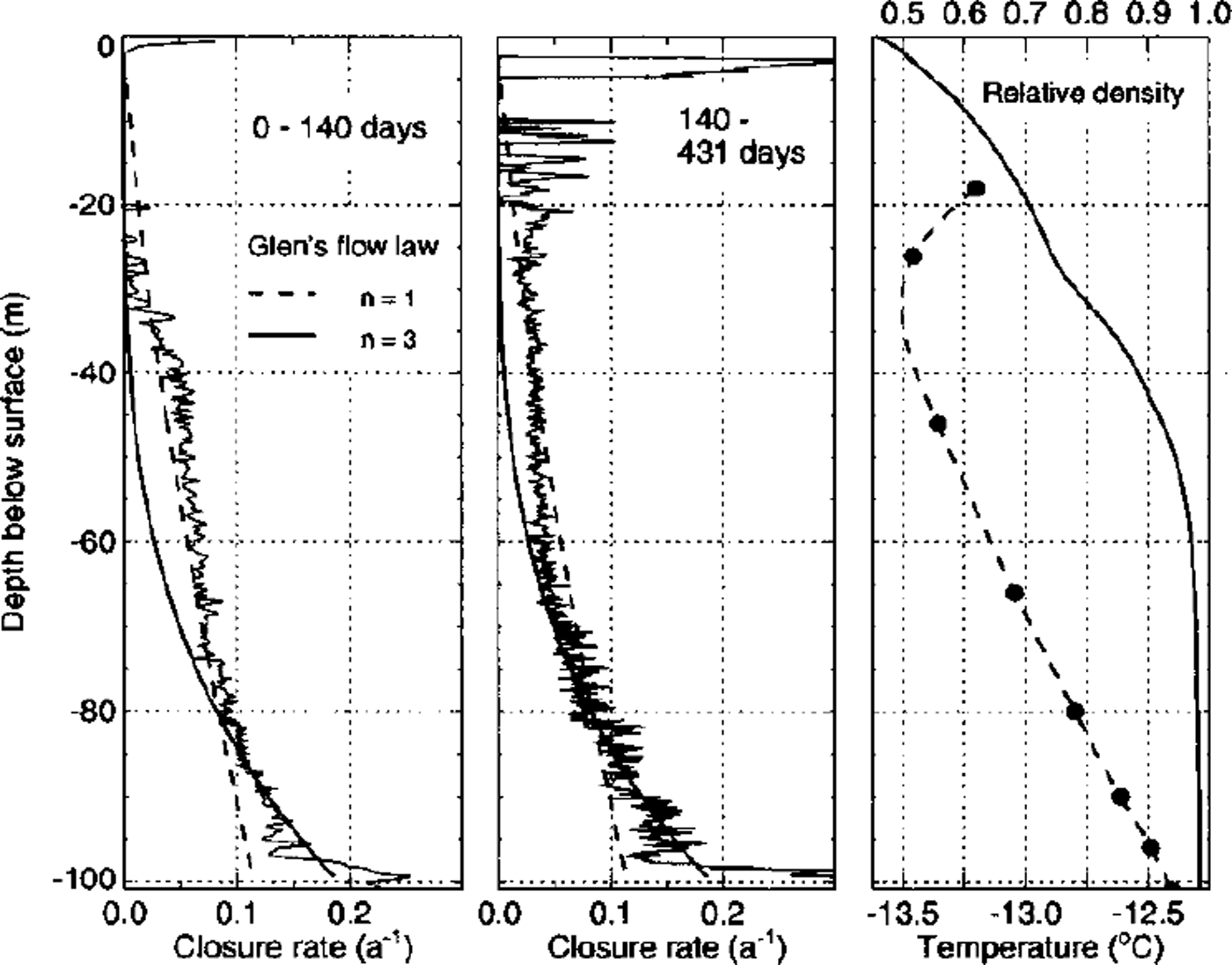
Fig. 4. Left and middle: Borehole-closure rates calculated from the borehole diameter measured after 140 and 431 days. Closure rates calculated with Nye’s formula for incompressible ice are shown with thick solid and dashed lines for n = 3 and n=l. Right: The smoothed firn density measured on the core (personal communication from R. Weisshaar, 1998) is shown as dimensionless relative density D=ρ/ρice. The dashed line is an interpolation of measured borehole temperatures indicated with dots.
Our measurements do not allow conclusions to be drawn about the eventual non-steady effects of borehole closure. These include the transient flow behavior of glacier ice detected in borehole closure measurements (Reference PatersonPaterson, 1977; Reference Naruse, Okuhira, Ohmae, Kawada and NakawoNaruse and others, 1988), as well as changing rheological properties due to firn densification. An interpretation of the measurements in terms of steady creep is attempted below.
The enlarged view of the closure rates near the bed in Figure 5 shows that the lowest 3 m exhibit enhanced deformation rates. A comparison with the high-resolution density profile measured at the University of Heidelberg (right panel of Fig. 5; personal communication from R. Weisshaar, 1998) reveals that narrow layers of low-density ice correspond to zones of enhanced borehole closure, especially at 94, 96 and 99 m depth. However, the high closure rates of the lowest 3 m cannot be explained by lower densities of the basal ice. Other possible explanations of this behavior are:
-
(i) The lowest part of the core exhibits a high impurity content (personal communication from L. Keck, 1999). This may cause altered rheological properties and thus enhanced deformation rates.
-
(ii) The steep bedrock slope at the drill site induces high deformation rates of the basal ice, which leads to a deformed borehole cross-section and thus to a reduced apparent diameter of the borehole. Indeed, exceptionally high tilt angles are observed in the lowest part of the borehole (see next subsection).
-
(iii) A thin zone of intense shear or a slip plane could cause the observed narrowing of the borehole diameter.
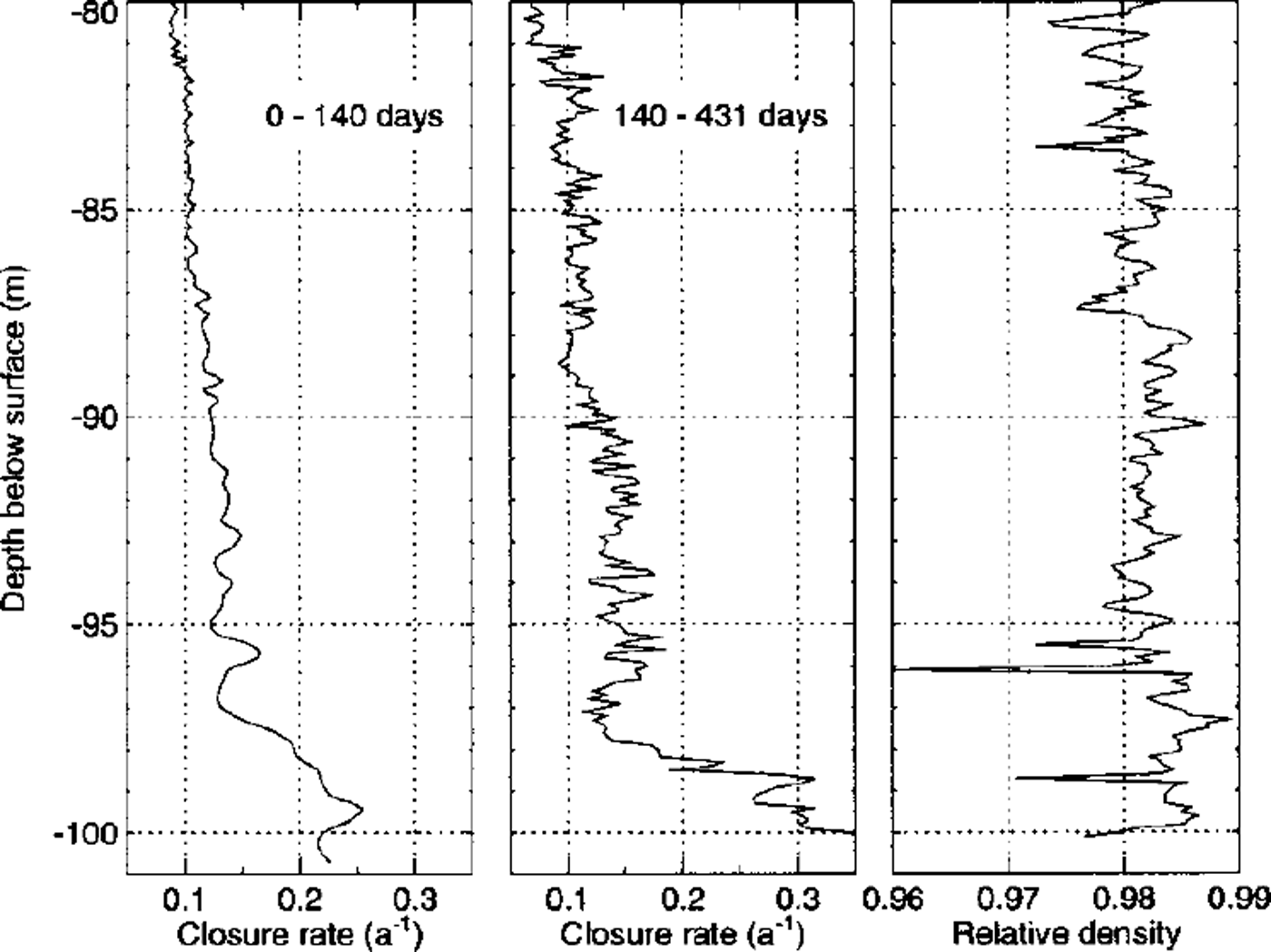
Fig. 5. An enlarged view of the bottom part of Figure 4. The borehole-closure rates are nearly constant during both time intervals between 80 and 97 m depth. Note the strongly enhanced closure rates in the lowest 3 m. The right panel shows the high-resolution density profile (personal communication from R. Weisshaar, 1998). Enhanced closure rates may be partly correlated to strata of lower density.
The observed constant closure rates near the bed favor the first two possibilities, which are likely to act together to produce the observed effect. It is impossible to determine the relative importance of their contributions from these measurements alone.
A similar abrupt change in closure rates has been observed in the lowest 3 m of a borehole in Devon Ice Cap, Canadian Arctic. Reference PatersonPaterson (1977) attributed this to the apparent softness of ice deposited during the Wisconsin glaciation, probably due to smaller grain-sizes and higher impurity content, but he also considered the effect of the small-scale bedrock topography to be a possible explanation.
Borehole tilt measurements
Five tiltmeters were installed 431 days after completion of borehole B95–2, at the bottom of the hole and 5, 15, 28, 48 and 68 m above bedrock. The tiltmeters were dual-axis electrolytic tilt cells with a measurement range of ±15° (HL-Planar NS15/V2, HL-Planartechmk GmbH). Each tiltmeter was individually calibrated to an accuracy of ±0.02° (by the method described in Reference Gudmundsson, Bauder, Luthi, Fischer and FunkGudmundsson and others, 1999; Reference LuthiLuthi, 1999) and was cased into a sealed steel tube with waterproof connectors. The uppermost tilt sensor never worked satisfactorily and is therefore excluded from further discussion.
The initial borehole inclination is not known, but from the fact that the drill cable never touched the borehole wall (personal communication from H. Rufli, 1998) a negligible maximum deviation of 0.12° from the vertical can be calculated. Readings of total tilt angle 90 just after installation in the borehole are listed inTable 1. Since the tiltmeters were only suspended on their cables, the measured tilt angles may deviate from the actual borehole inclination. An upper bound Δθmax can be calculated with the borehole diameter which was measured at the same time. Unless the borehole curvature is large, the sensor is in contact with the borehole wall, and thus the measured tilt angles are interpreted as borehole inclination except possibly at the lowest inclinometer. Tiltmeter CI was outside the calibrated measurement range after 431 days. Comparison with the other tiltmeters shows that exceptional deformation must have taken place, and the calculated tilt rates 90 exceed those of the other inclinometers by at least a factor of 5.
Table 1. Tilt measurements of the inclinometers installed in borehole B95–2
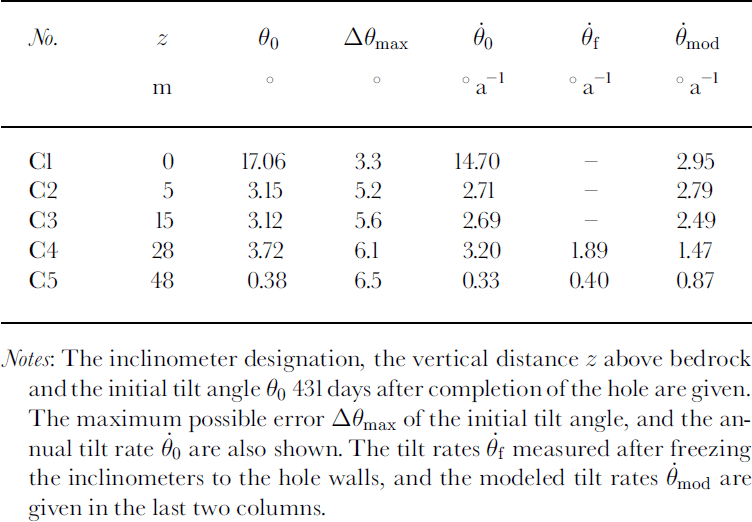
Average borehole tilt rates measured after freezing the inclinometers to the borehole walls are shown in the 0{ column inTable 1. The lowest three tilt sensors were outside the calibrated measurement range, presumably due to some insulation error, and are therefore ignored.
Firn temperature
Firn temperatures were measured below the zone of annual variation with eight thermistors calibrated to an accuracy of ±0.05 °C. The temperature profile, shown with a dashed line in Figure 4, exhibits a marked bend towards warmer temperatures at 30 m depth. Such a feature has not been observed so far on Colle Gmfetti, and an earlier modeling study concluded that firn temperatures were in a steady state in 1983 (Reference Haeberli and FunkHaeberli and Funk, 1991). With a transient heat-flow model of Monte Rosa, taking account of the geometry, possible permafrost degradation, density-dependent conductivities and ice advection, the bend could be attributed to the decadal warming trend observed at nearby meteorological stations (Reference LuthiLuthi, 1999). These questions will be addressed in a subsequent paper.
Rheology of Gold Firn
Mechanical and thermal properties of snow and firn are strongly dependent on the density (e.g. Reference MellorMellor, 1977; Reference DuvalDuval, 1985). Firn compaction is the dominant deformation process in the near-surface part of polar accumulation areas and has been studied by many authors (e.g. Reference BaderBader, 1962; Reference Herron and LangwayHerron and Langway, 1980). Many firn-deformation experiments under complex load conditions have been performed in situ as well as in the laboratory (e.g. Reference LandauerLandauer, 1957a, b; Reference Ebinuma and MaenoEbinuma and Maeno, 1985).
While on a microscopic scale the whole complexity of the sintering processes has to be taken into account, it is desirable to use a relatively simple flow law for simulating the flow behavior of a whole glacier. Such a relation provides an averaged response of the effects of stress concentrations around voids or between the contact areas of neighboring grains. This connection of microscopic processes to a macroscopic scale is conveniently expressed in terms of a scalar strain-rate potential (Reference CocksCocks, 1994; Reference Ponte Castañeda and SuquetPonte Gastaheda and Suquet, 1998).
Flow laws formulated in terms of an isotropic, viscous, compressible fluid are used in this study, where effective viscosities are dependent on the stress state and on temperature and density as scalar state variables. In the limit of full density this constitutive equation should take the form of a power-law fluid (i.e. Glen’s flow law).
Denoting the stress tensor by σlp
the mean stress is
![]() and the stress deviator tensor
and the stress deviator tensor
![]() . Glen’s flow law is written as
. Glen’s flow law is written as
where A0
and n are flow-law parameters and the effective shear stress is defined by
![]() It is assumed that the temperature dependence may be separated into a multiplicative factor B(T).
It is assumed that the temperature dependence may be separated into a multiplicative factor B(T).
The flow law for a power-law creeping material containing spherical voids (Reference Sofronis and McMeekingSofroms and McMeeking, 1992; Reference CocksCocks, 1994) extends Equation (2) to include a compressible part proportional to σ–m. Two parameters a(D) and b(D) describing the influence of the relative firn density D = p/ρice
(where ρice
= 917 kg m–3) are introduced. The strain rates
![]() depend on the stress deviator tensor
depend on the stress deviator tensor
![]() and the mean stress according to the relation
and the mean stress according to the relation

where the ˚effective" effective shear stress σD is defined as
In the limit of full density (D → 1) the contribution of the compressible part must vanish so that Glen’s flow law is recovered. These requirements restrain the limiting behavior of the parameters to
The parameter b(D) can be derived analytically for the isotropic compression of a power-law creeping material containing spherical voids (Reference Wilkinson and AshbyWilkinson and Ashby, 1975), resulting in

(subscript ˚0" indicates that this result is valid only at high densities). The factor a(D) was calculated by several authors who obtained slightly different parameterizations (Reference Sofronis and McMeekingSofroms and McMeeking, 1992; Reference Duva and CrowDuva and Grow, 1994). We will use the one derived by Duva and Grow (employed by Reference Gagliardini and MeyssonnierGagliardim and Meyssonnier, 1997),

The flow-law parameters σ0(D) and b0(D) given in these studies are valid only at relative densities exceeding D = 0.8. Altered grain contacts and additional diffusive processes operate at lower densities and require a different flow law. Alternatively they can be approximately taken into account in a suitable parameterization. Based on the density profile of Site 2, Greenland, such a parameterization has been derived by Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (1997). Their equation (15) (corrected for a typographic error; personal communication from O. Gagliardini, 1998) reads

These parameterizations are shown in Figure 6 and correspond to the orders-of-magnitude variation of firn viscosity with density found in experimental studies (e.g. Reference MellorMellor, 1977).
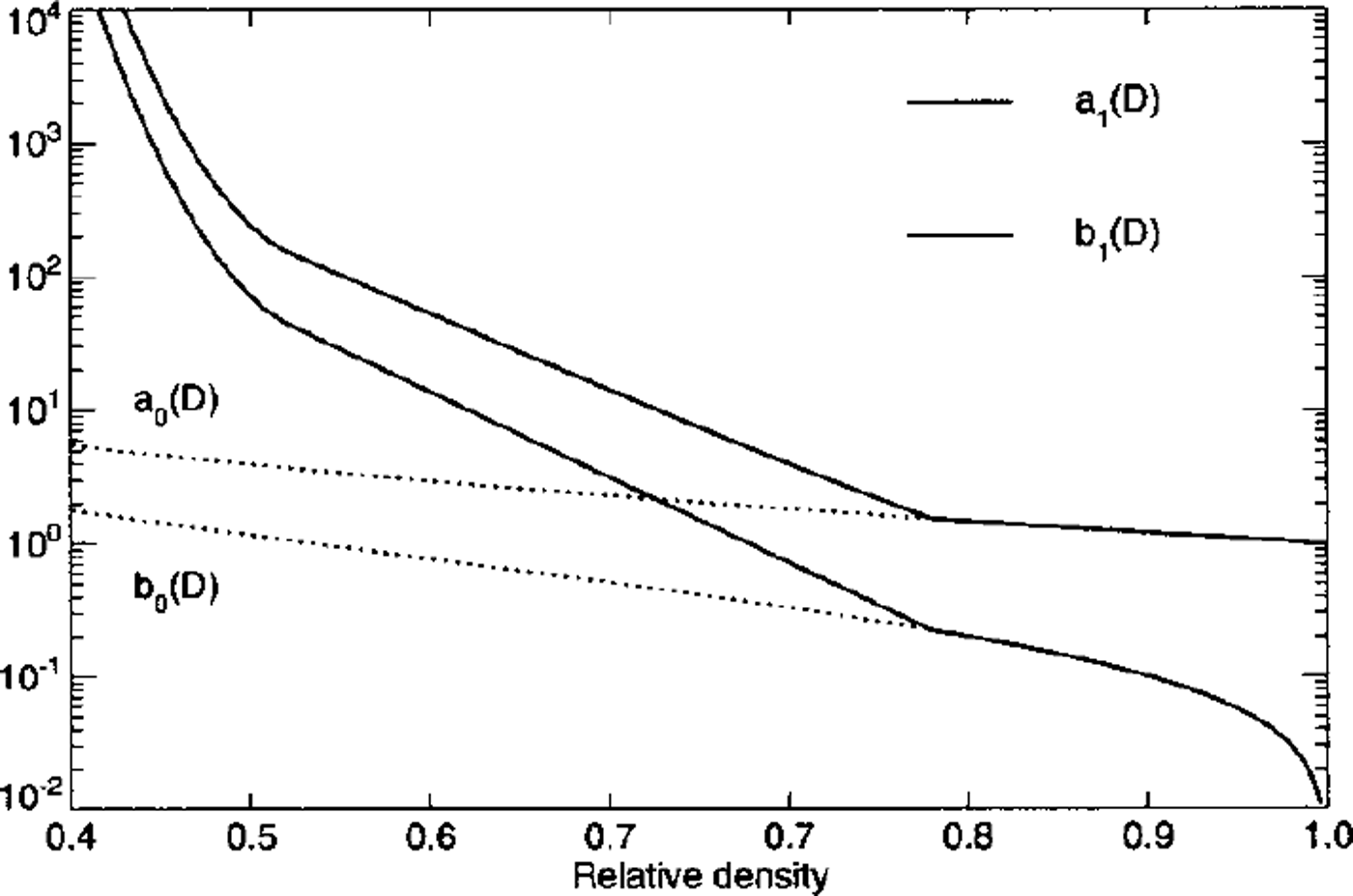
Fig. 6. Density dependence of the flow-law parameters a1(D) (solid line) and b1D) (dashed line) in the flow law for coldfirn. The functions σ0(D) and b0(D), valid at high densities, are indicated with dotted lines for comparison.
Flow-law parameters
The parameter A0 = 0.0264 bar a"1 (8.33 × KT16 sȡ1 kPa–3) at a temperature of –10°C (1.7 times the value recommended by Reference PatersonPaterson, 1994, p. 97) and a flow-law exponent n = 3 were used throughout this study. The dependency on the temperature T (in degrees Celsius) of the rate factor was taken from Reference Smith and MorlandSmith and Morland (1981):
Bubble close-off
The firn close-off density is the paramount quantity biasing the amount of densification in the high-pressure part of the glacier (Reference Salamatin and DuvalSalamatin and Duval, 1997). Since the exact bubble close-off density is not known for Colle Gnifetti, model runs were conducted with densities of 780, 825 and 917 kg m–3 (relative densities 0.85, 0.9 and 1.0). The effects of the pressure Ph in trapped air bubbles on densification was taken into account by replacing σm in Equation (3) with σm + ρh. From the state equation of ideal gases we obtain

where subscript ˚c" denotes quantities at close-off The pressure Pc at close-off is the mean atmospheric pressure which is about 740 hPa at Colle Gmfetti.
Flow Model
The data presented in previous sections can be interpreted with the help of numerical flow models. The constitutive equations (3) for cold firn were implemented in two finite-element (FE) codes, FEMTOOL (Reference Rutschmann, Morgan, Ofiate, Periaux, Periaire and ZienkiewiczRutschmann, 1993; a universal FE-solver developed at VAW, ETH Zürich) and MARC (commercial software). Two-dimensional plane-strain calculations were performed using eight-node isoparametric, arbitrary quadrilateral elements with biquadratic interpolation and Galerkin weighting. The three-dimensional model was run using a 20–node isoparametric hexahedral brick element with triquadratic interpolation. These elements have quadratic interpolation for the velocity and linear interpolation for pressure. The densities and the temperatures are given as scalar state variables at all nodes and thus are also interpolated quadratically
The accuracy of the models was checked for model geometries and load conditions with known analytical solutions, resulting in maximum velocity differences of 1% (Reference LuthiLuthi, 1999). Comparisons of model runs performed with both codes on the same mesh differed by ω1 % for complex model geometries.
Borehole-closure model
The borehole-closure experiment described above was analyzed with a cylindrical^ symmetric flow model. Measured densities and temperatures were prescribed and a density-dependent gravity force was applied. The borehole wall was kept stress-free, and the nodes at the bed were fixed in the vertical direction but were free to move horizontally. The boundary condition at the outer vertical margin (one ice thickness from the center) was either a prescribed horizontal stress or fixed nodes in the radial direction. Identical results were obtained for both boundary conditions.
Model results for incompressible ice (D = 1, i.e. Glen’s flow law) were compared to the analytical solution for the closure rate s and the radial velocity τ of a hole with radius R and a compressive stress P far from the hole (Reference NyeNye, 1953):

Interpreting measured borehole-closure rates with this formula is not strictly valid, since the assumption of an infinite medium with a uniform stress at infinity is not fulfilled. However the difference compared to numerical solutions taking into account the full stress field is small. Equation (10) was evaluated at all depths h with the overburden load P(h) and for flow-law exponents n = 1 and n = 3. Measured borehole temperatures were taken into account in the parameter B(T), and the flow-law parameter A0 was used as a scaling factor in order to match the measured borehole-closure rates.
Comparing these results with the measured closure rates (Fig. 4, middle panel) shows that the lowest 40 m of the borehole, where the densities are close to the density of ice, are reasonably fitted with flow-law parameters n = 3 and A0 = 4.9×10–16 s–1 KPa–3 6 6 6 6 6 6 6 6 , 6 the value for –10°C recommended by Reference PatersonPaterson (1994, p. 97). In the upper part of the borehole, n = 1 seems more appropriate. It is clear, however, that the observed constant closure rate at 40–60 m depth cannot be obtained with any formula relying on Glen’s flow law. Moreover, the assumption of incompressibility clearly fails to explain the measured large closure rates in the uppermost 20 m of the borehole.
Borehole-closure rates modeled with the firn flow law (Equation (3)) and the flow-law parameters discussed above are compared to the measurements of the second period (140–431 days) in Figure 7. Below 40 m, the measured closure rate is perfectly reproduced by the model. Modeled closure rates are greatly enhanced in the uppermost 30 m where relative firn densities are ω0.8 and where measured closure rates are also enhanced. From the progressive densification of firn one would expect the modeled closure rates, which were calculated with the initial density profile, to give an upper bound. Differences between the high-resolution density profile (measured at the University of Heidelberg; personal communication from R. Weisshaar, 1998) and the smooth density profile (Fig. 4) show the large inhomogeneity of the firn near the surface. Ice lenses and frequent icy layers of refrozen meltwater have been observed in snow pits (Reference Mean, Haeberli and SchadlerMean and others, 1984). These layers induce large viscosity variations and are likely to strengthen the firn and thus to slow down the closure of the borehole.
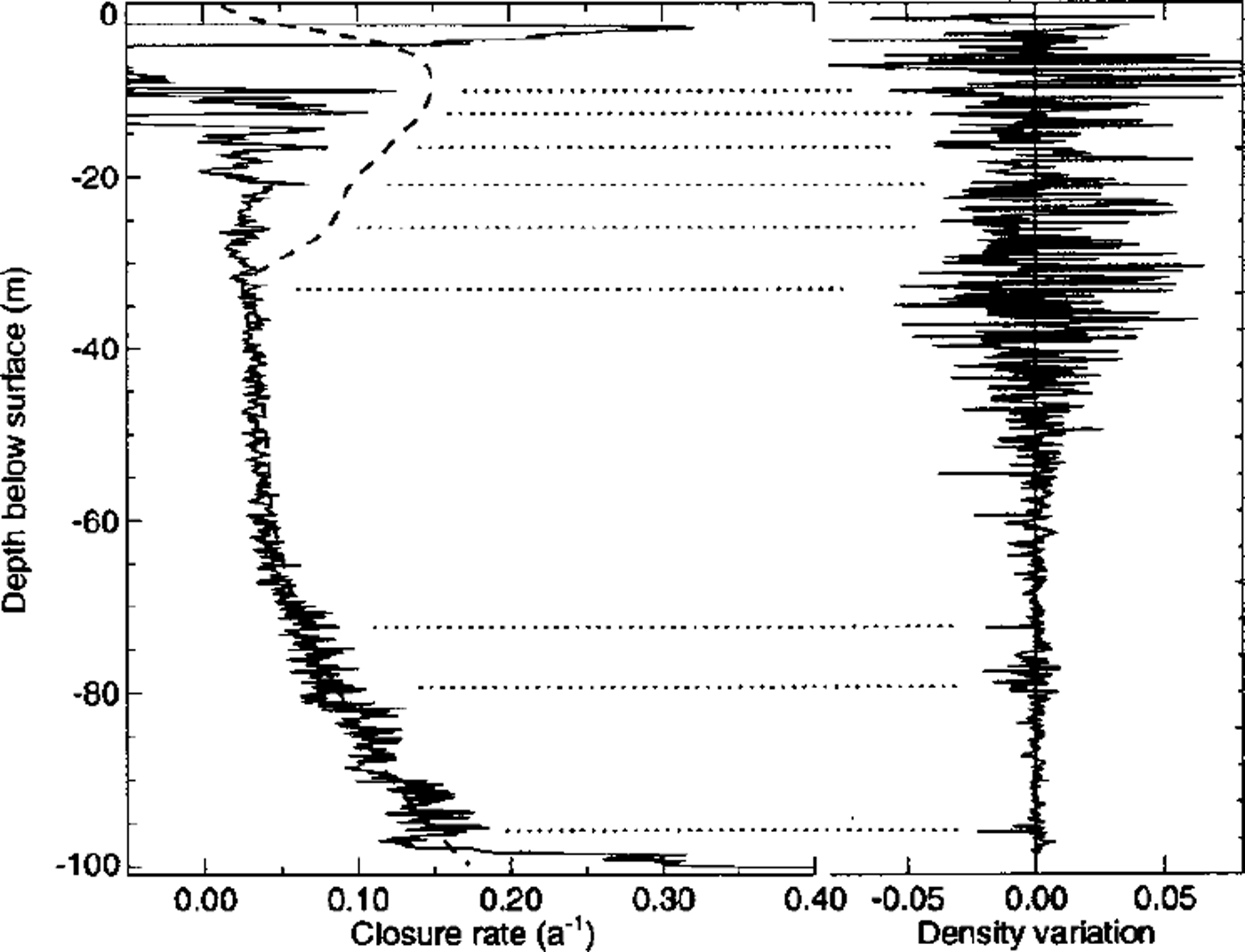
Fig. 7. Left: Borehole-closure rates modeled with the firn flow law (dashed line) are compared to measured closure rates between 140 and 431 days. Right: Differences between the high-resolution firn-density profile measured on the core (personal communication from R. Weisshaar, 1998) and the smooth firn-density profile are given as relative density. Horizontal dotted lines help identify layers of enhanced closure rates with low-density firn.
A further possible source of disagreement is that the firn flow law (Equation (3)) is not appropriate at strongly deviatoric stress states at low densities. The assumption of a constant ratio of the density-dependent factors (i.e. ajh = σ0/b0 in Equation (8)) is justified neither by theory nor by observation. A flow law taking better account of the physical processes involved in the deformation of firn at low densities is likely to give different results.
We believe that the nearly perfect overall agreement of modeled and measured borehole-closure rates at relative densities of >0.8 suggests that the non-steady effects in the borehole closure are small and that the firn flow law suitably describes firn deformation in cold glaciers. The model results presented below show that the flow law is appropriate for modeling the steady creep of glacier flow under mildly deviatoric stress states.
Flowline Model of Colle Gnifetti
A two-dimensional flow model along an approximate flowline is shown in Figure 8. Starting below Punta Gmfetti, it passes through the borehole locations B95–1, B82–2 and B95–2 (thick dashed line in Fig. 1) and ends at the big crevasse in the outflow to Grenzgletscher. This flowline follows a radar profile where surface velocities were measured at nine stakes. The model is used to estimate the influence of boundary conditions and physical properties of the firn on the flow field. Several quantities were varied in a parameter study in order to assess their relative importance, namely, the firn temperature profile, the firn density distribution, the flow law (firn rheology), the firn close-off density ρc and the mechanical boundary condition at the outflow to Grenzgletscher (Reference LuthiLüthi, 1999).
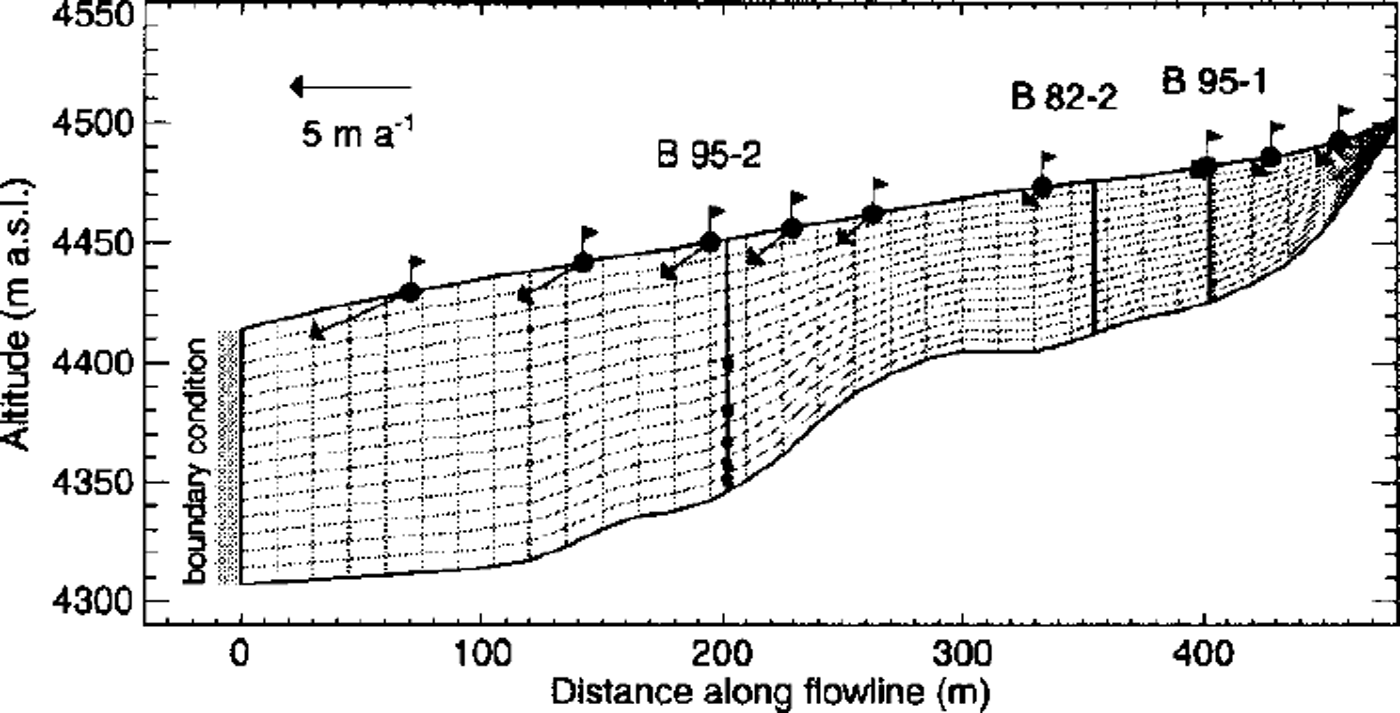
Fig. 8. The FE mesh of the flowline model of Colle Gnifetti. The geometry of the mesh is based on digital terrain models of the glacier surface and the glacier bed, and the grid consists of 480 elements. The locations of three boreholes are indicated with thick vertical lines. Surface velocities were measured at stakes signified by flags. The approximate position of the inclinometers is represented by black boxes in borehole B95–2. Mechanical boundary conditions are prescribed at the left margin (gray shaded), as explained in Figure 9.
The model relies on the assumption of a steady state of the geometry, the density profile and the measured ice temperatures. While the surface elevation did not change notably during the last century (Reference WagnerWagner, 1996), englacial temperatures are not in a stationary state, as was revealed with a transient heat-flow model (Reference LuthiLüthi, 1999).
Ages of chemically dated layers in ice cores and surface velocities measured at nine stakes on the flowline were used as benchmark for the validity of the model calculation. Stake positions were measured five times at intervals of 4 months to an accuracy of 25–35 mm. The measured progressive stake inclination was taken into account in calculating the velocities, which are accurate to ±0.1 m a"1.
The mechanical boundary condition at the left margin of the model, which corresponds to the outflow into Grenzgletscher, is not known. An abrupt increase of surface slope (up to 30°) and an unknown bed topography lead to the formation of a huge crevasse of undetermined depth. Consequently, the horizontal stresses at the left boundary have to be parameterized. We assume a crevasse of depth hc which is stress-free, and a linear increase of horizontal stresses below (Fig. 9). The vertical gradient of the prescribed horizontal stress is set to k = 0.1 bar m–1.
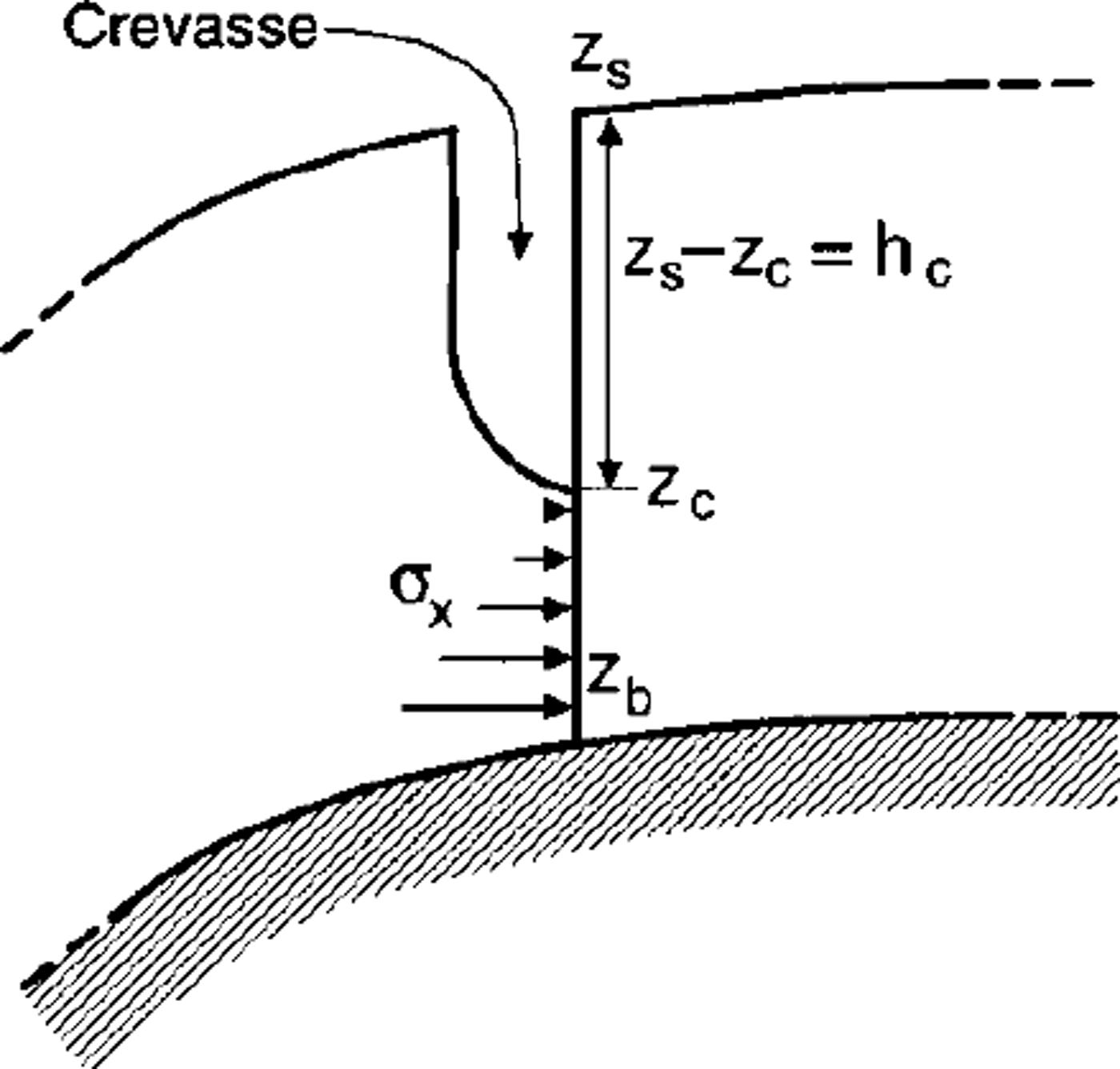
Fig. 9. A sketch of the quantities used to parameterize the stress boundary condition at the large crevasse in the outflow to Grenzgletscher. The depth of the crevasse, where the wall is kept stress-free, is hc = zs ― zc. Below, a linearly increasing horizontal stress σxx(z) = k(zc ― z) is prescribed. The parameter zc is varied in different model runs. The modeled geometry (Fig. 8) is on the righthand side of the crevasse.
A flow model at a constant temperature of –13°C, a crevasse depth of 30 m, a horizontal stress gradient k = 0.1 bar m–1 and a constant density profile along the flowline was used as reference in the parameter study (later referred to as ˚reference model").
While it is clear that a flowline model is a poor approximation in the downstream part of the model geometry where ice flow is largely influenced by the topography in three dimensions, it is likely to be a reasonable approximation of the ice flow in the upper part of the glacier. However, also in this range a horizontal stretching perpendicular to the main ice flow has been measured, which should be kept in mind in interpreting the model results.
The flow velocities calculated with the reference model are plotted on several cross-sections in the lower part of Figure 10. A qualitative comparison with velocities measured at nine stakes shows a good agreement in the region between the boreholes. A noteworthy feature is the unusual shape of the velocity profiles, with an increasing horizontal velocity near the surface. This is a consequence of the low viscosity of the firn layer. A quantitative comparison of modeled and measured surface velocities is shown in the upper part of Figure 10. Substantial deviations occur towards the left model margin because of the inaccurate boundary condition at the big crevasse.
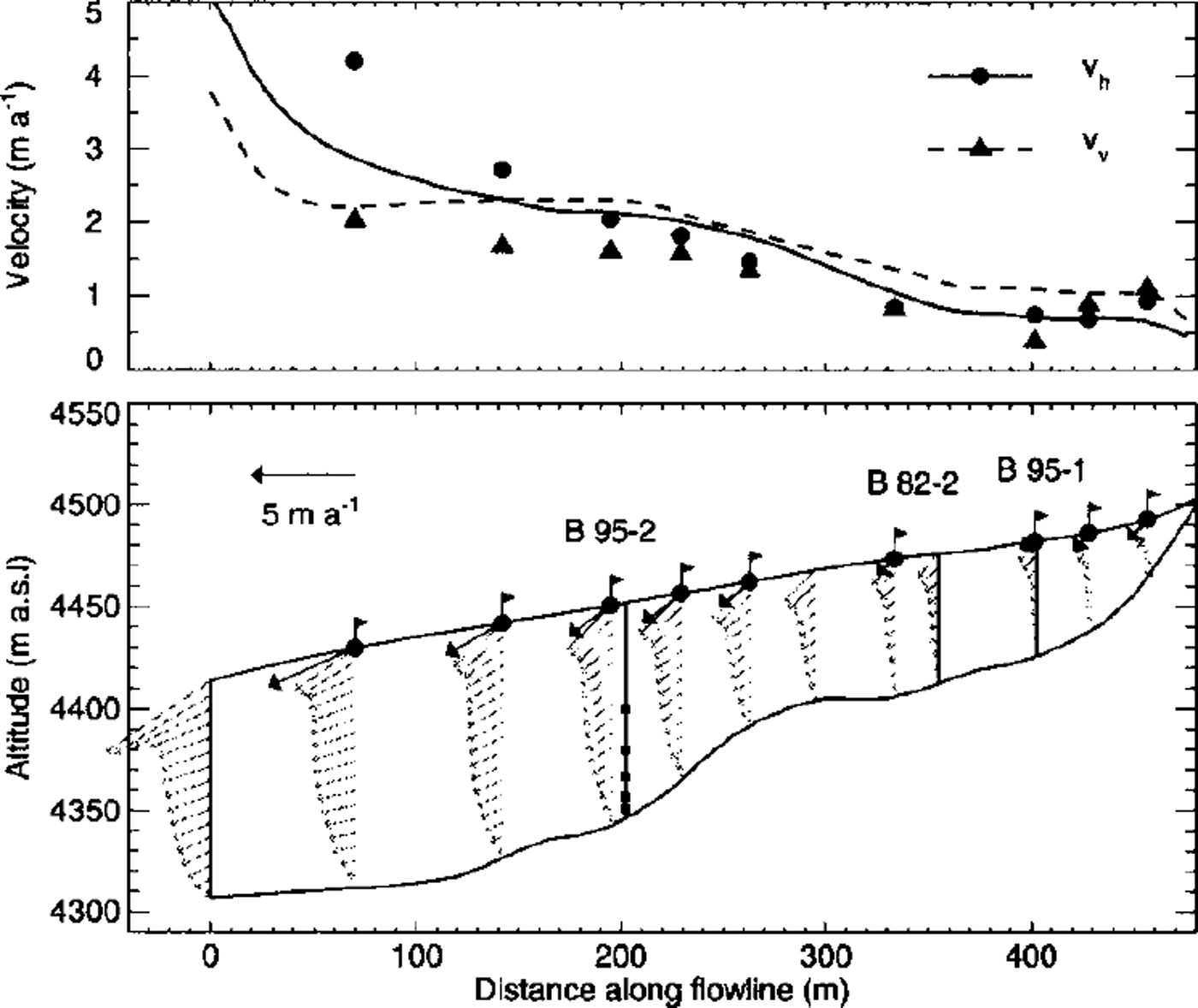
Fig. 10. Comparison of modeled surface velocities from the reference model run with velocities measured at stakes. Absolute values of the modeled horizontal (solid line) and vertical (dashed line) velocity are shown in the upper graph. Measurements are indicated with dots for the horizontal, and triangles for the vertical, velocity component. The lower graph shows the flow field at the position of the stakes. Note the unusual shape of the velocity profiles, with an increase of horizontal velocities near the surface. This is an effect of the low viscosity of the firn layer.
Three-Dimensional Flow Model
The geometry of the three-dimensional flow model of Colle Gmfetti is based on the surface topography and the ice-thickness map shown in Figures 1 and 2. Average temperature and density profiles were prescribed and the depth of the crevasse in the outflow to Grenzgletscher was set to hc = 60 m (Fig. 9). Relative close-off densities of Dc = 0.85 and 0.9 were used in Equation (9).
Modeled surface velocities are shown in Figure 11 together with velocities measured at stakes (Reference Haeberli, Schmid and WagenbachHaeberli and others, 1988; Reference WagnerWagner, 1996; Reference LuthiLuthi, 1999). A good agreement of the flow direction and the speed is obtained in the southeastern part of the glacier where most boreholes are located. The larger differences in the northwestern part stem from several inaccuracies in the model input. Main problems are the glacier bed which is only approximately known due to the narrow valley rendering it difficult to interpret radar measurements, and poorly determined ice temperatures towards Zumsteinspitze, which are known to be considerably higher than in the southeastern part of Colle Gnifetti (Reference Haeberli and AleanHaeberli and Alean, 1985).
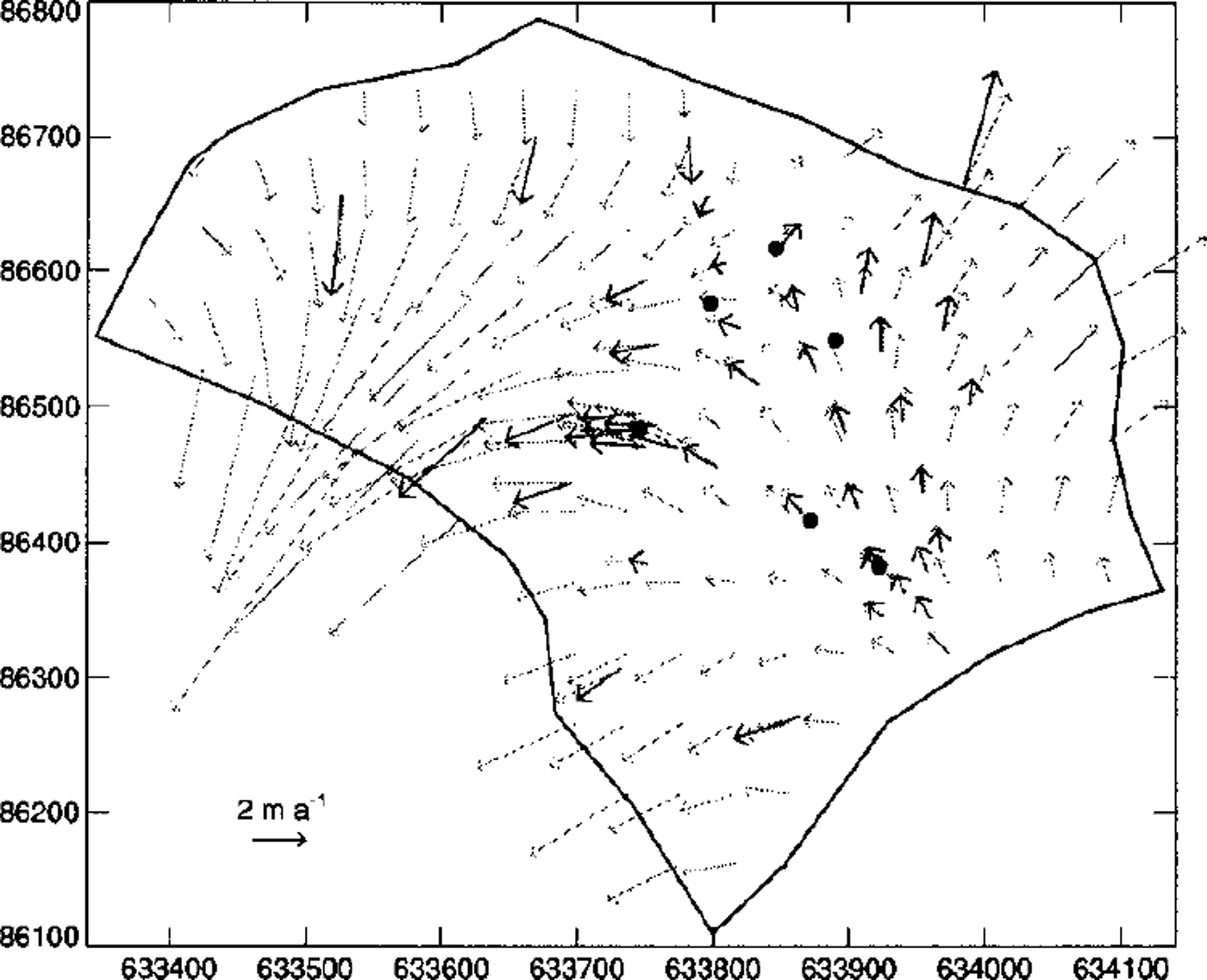
Fig. 11. Comparison of surface velocities from the three-dimensional flow model (gray arrows) with measured surface velocities (black arrows).
The modeled velocity field was used to calculate the inclination of the tiltmeters with the method described by Reference Gudmundsson, Bauder, Luthi, Fischer and FunkGudmundsson and others (1999). Calculated annual tilt rates 9mod are compared to measurements in Table 1. All measured tilt rates are reasonably reproduced by the flow model except for the lowest inclinometer, CI, which exhibits a greatly enhanced tilt rate.
Firn-densification model
The firn densification was calculated on the same model grid with an altered FE heat-transfer code, including streamline-upwind Petrov-Galerkin weighting. As model input the velocity field from the flow model was used, together with a constant density of 410 kg m–33 (D = 0.45) as surface boundary condition. Starting from an approximate initial density distribution, the flow model and the densification model were run iteratively Due to the slow convergence rate of the fixed point iteration, some 200 steps were necessary until convergence was obtained. The solution of the fully coupled system in three dimensions is therefore very restricted by the enormous computation times.
The resulting densities are compared to smoothed measured density profiles in Figure 12. The agreement is very good for all cores except B82–1, where the measured constant density below 50 m seems unrealistic. All measured density profiles are bent towards lower values at 20–30 m depth. This feature cannot be reproduced by the model, indicating either an incorrect firn rheology or a climatic signal. The density anomaly occurs at different densities in different cores, but corresponds to the time-span 1940–50. We therefore presume that this anomaly is due to some climatic effect, most probably a variation in accumulation rate or surface temperature.
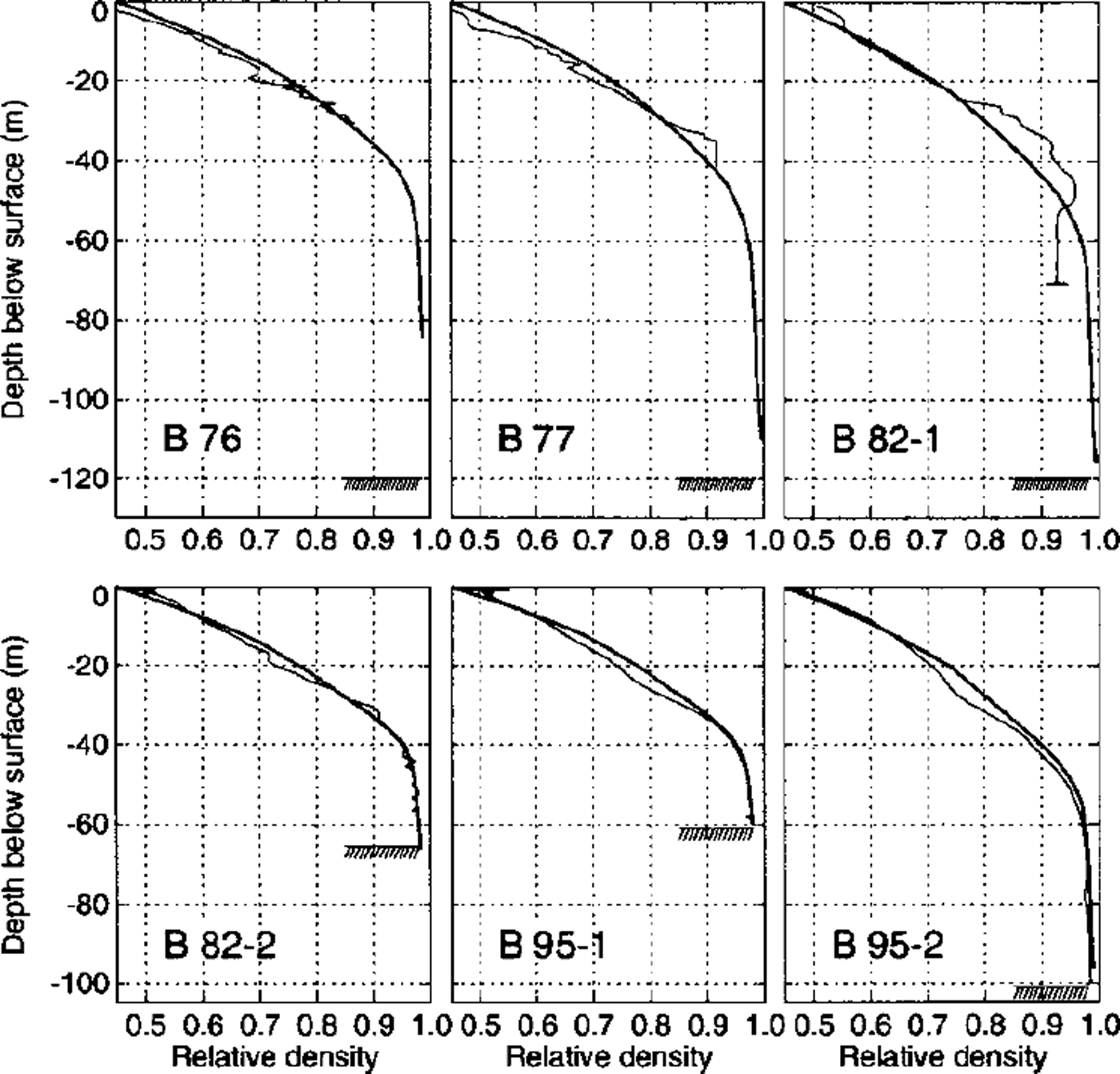
Fig. 12. Fun densities calculated with the coupled three-dimensional models (thick lines), compared with smoothed density profiles measured on six deep cores (thin lines).
Dating of ice cores
Large seasonal variations in accumulation and wind erosion render it difficult to date ice cores from Colle Gnifetti by counting annual layers. Reference datings have been derived for layers containing bomb tritium, as well as for unique patterns of Sahara dust events (Wagenbach and Geis, 1989; Reference Doscher, Gaggeler, Schotterer and SchwikowskiDoscher and others, 1995; Reference Gaggeler, Stauffer, Doscher and BlunierGaggeler and others, 1997). Other layers have been dated by matching known volcanic eruptions and Sahara dust events to layers of high acid or dust concentration. Datings have been given for the four deep cores and two cores not reaching bedrock, namely, B76 and B77 (Reference Schotterer, Haeberli, Good, Oeschger and RothlisbergerSchotterer and others, 1981). Depth-age relations compliant with the three-dimensional flow model of Reference WagnerWagner (1996) have been established for cores 82–1 (blue core, data from Reference Doscher, Gaggeler, Schotterer and SchwikowskiDoscher and others, 1995, Reference Doscher, Gaggeler, Schotterer and Schwikowski1996; Reference Gaggeler, Stauffer, Doscher and BlunierGaggeler and others, 1997; personal communication from M. Schwikowski, 1998; personal communication from A. Daellenbach, 1999; Reference Schwikowski, Doscher, Gaggeler and SchottererSchwikowski and others, 1999) and B82–2 (Reference SchaferSchafer, 1995). Preliminary datings have been accomplished for the recently drilled cores B95–1 and B95–2 (personal communication from L. Keck, 1999). All dated layers are indicated with dots in Figures 13 and 14.
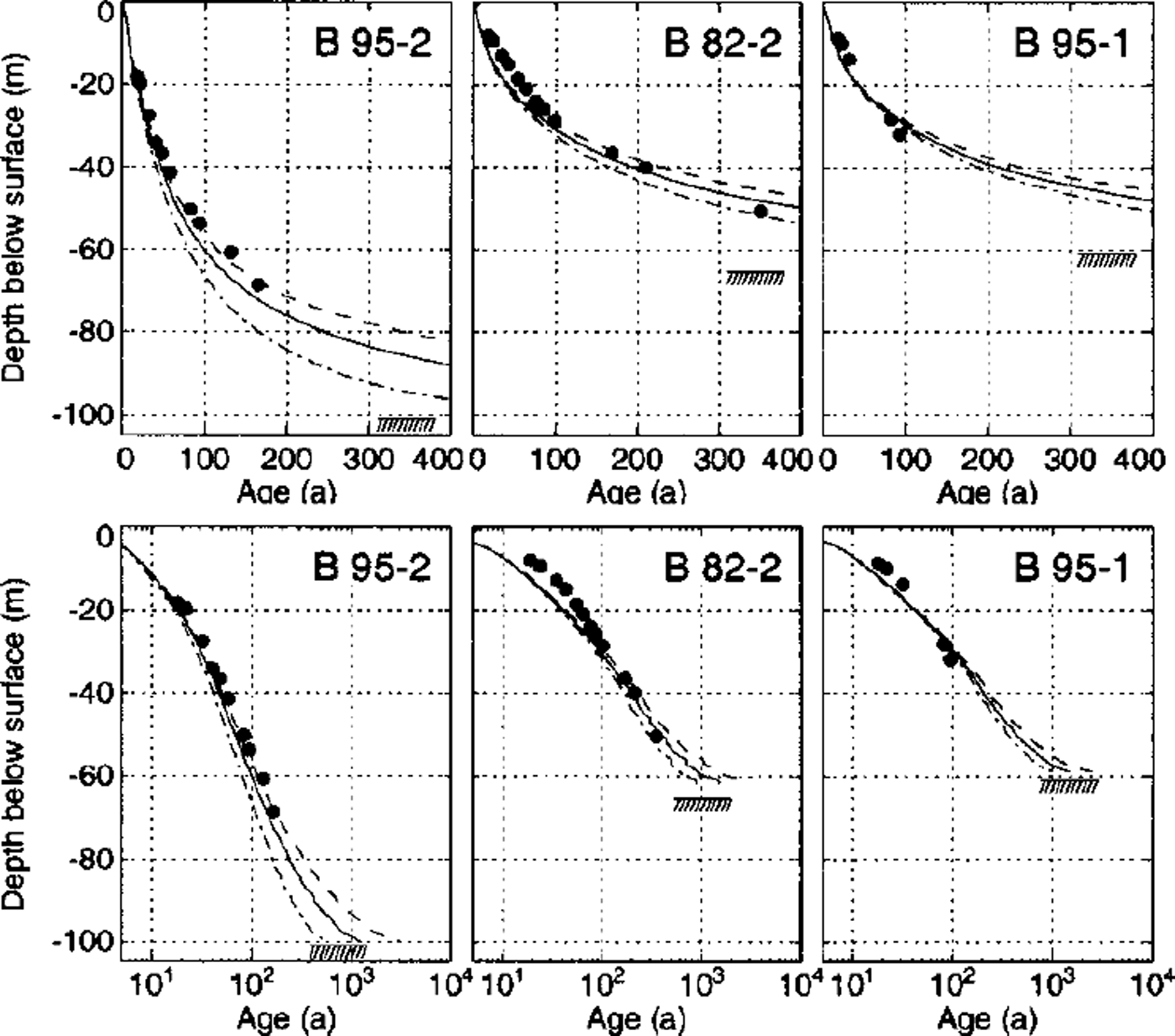
Fig. 13. Comparison of the measured depth-age relation with results from the flowline model. The solid line indicates results from the reference model run; black dots represent dated layers from chemical analyses. Bedrock is indicated by the hatched area. Datings from two model runs with altered close-off density are shown with a dashed line (Dc =0.85) and a dash-dotted line (Dc =1). The lower plot shows the same datings on a logarithmic time-scale.
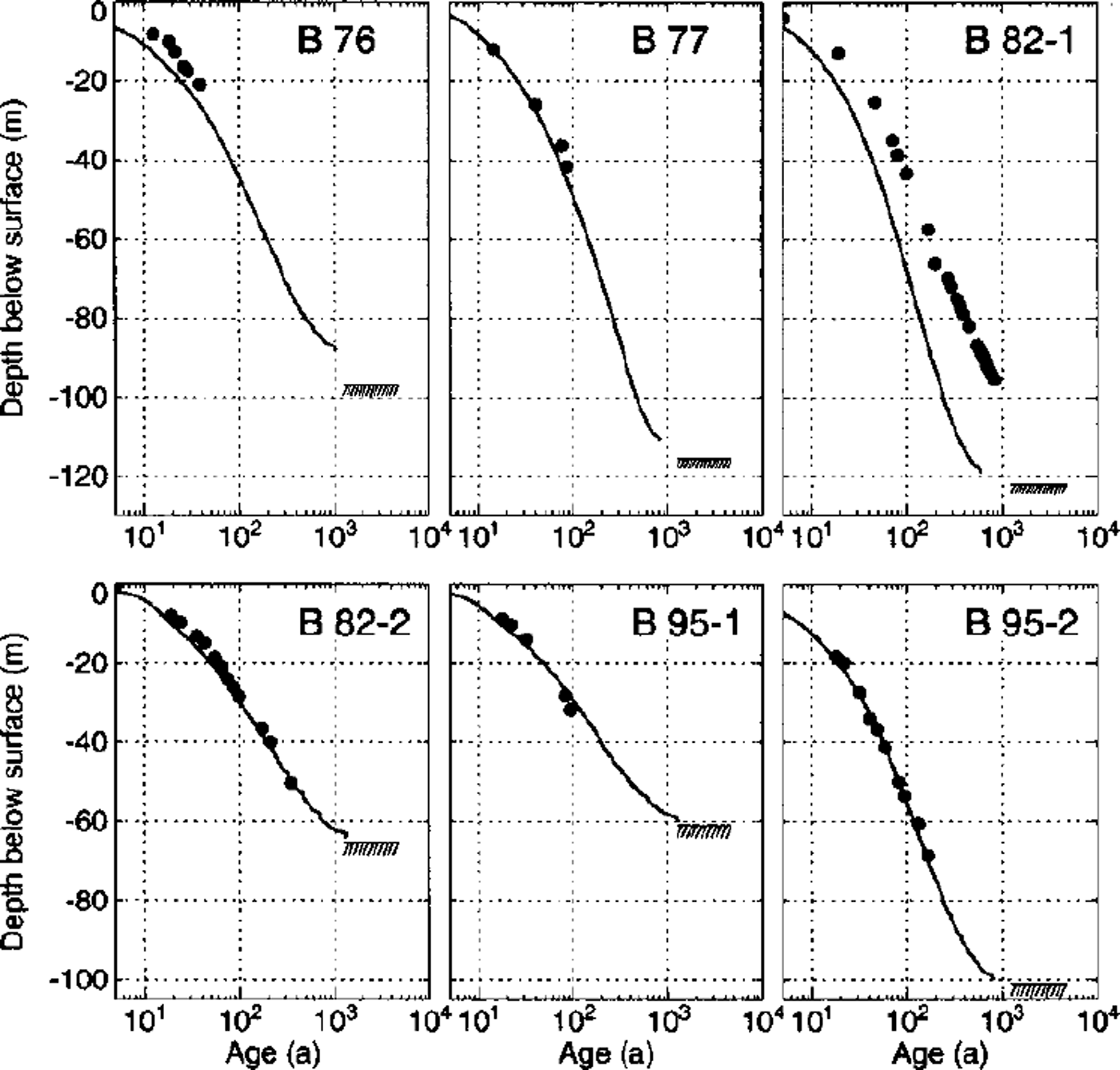
Fig. 14. Datings of six deep cores with the three-dimensional flow model. The depth of the bedrock is indicated with a hatched area.
Glacier flow models provide independent constraints on the dating of the cores. Depth-age relations were calculated by backtracking modeled flowlines starting at the boreholes. This was accomplished using a Runge-Kutta method and interpolating the velocities with the element shape functions. The depth-age relations calculated with the flowline model are plotted in Figure 13. Avery good agreement of measured and modeled ages is obtained for all three cores located on the flowline. Results from two model runs with altered close-off densities are also shown in Figure 13. As would be expected, the ice is younger if the effects of bubble close-off are neglected (Dc = 1, dash-dotted lines) and older if the close-off density is diminished (Dc = 0.85, dashed lines).
It is interesting to observe that the model predicts the youngest basal ice in the deepest core B95–2. This is certainly an effect of the high submergence velocities and thus higher accumulation rates around the drill site (Fig. 10; accumulation rates are largely determined by the submergence velocity on Colle Gnifetti, which is an effect of accumulation redistribution by wind drift). Increasing flow velocities together with a considerable increase in ice thickness along the flowline thus lead to an enhanced downward advection of younger ice.
The depth-age relations calculated with the three-dimensional flow model are presented in Figure 14. The agreement with chemically dated layers is good, except for core B82–1. This drill site is located close to the saddle point where horizontal surface velocities vanish. The depth-age relation thus depends critically on the precise local density and velocity field. Several inaccuracies in the model input, mentioned in the discussion of the velocity field, influence the saddle-point position and thus the dating of this core.
The other five cores have been drilled in locations where the surface velocities are well reproduced by the model. The good agreement of modeled ages with the dated layers allows dating to be continued down to the glacier bed (Fig. 14). The maximum modeled age of the ice some meters above the glacier bed is 1000–2000 years. However, the model geometry and the boundary conditions are not accurate enough to calculate the age of the ice close to the glacier bed.
Basal ice
The age of the basal ice cannot be predicted with the flow models discussed above. The bedrock topography is not known in sufficient detail to model flow disturbances caused by small-scale bedrock undulations. These could lead to disturbed isochrones or folds, and old ice could be trapped in overdeepenings by flow separation (Reference GudmundssonGudmundsson, 1997).
Transient effects of an evolving glacier geometry, changing accumulation rates and ice temperatures were not taken into account in the models which are based on steady conditions. The bubble close-off density is temperature-dependent (Reference Martinerie, Lipenkov, Raynaud, Chappellaz, Barkov and LoriusMartinene, 1994) and would thus be affected by changes of englacial temperature. In the discussion of Figure 13, we found a strong dependence of the age of basal ice on the close-off density. This implies that colder firn temperatures in the past would have increased the close-off density, therefore inducing slightly younger basal ice. A counteracting effect was detected by Reference Gaggeler, Stauffer, Doscher and BlunierGaggeler and others (1997) who found that air is isolated from the atmosphere by ice layers at densities of about 700 kg m–3. This would lead to higher air pressures at bubble close-off, a lower effective close-off density and older basal ice.
In both the borehole-closure and the borehole-inclination experiments we observed an enhanced deformation of the basal ice, which is likely to be caused by special Geological properties. This conclusion is corroborated by recent investigations on ice-core samples (personal communication from L. Keck, 1999).
Conclusion
The flow law for cold firn proposed by Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (1997) proved to be suitable for glacier flow models. The measured closure of a 100 m deep borehole was excellently reproduced where relative firn densities exceed 0.8. Enhanced closure rates are predicted by the model at lower densities, which could only partially be observed. We attribute this difference mainly to ice layers altering the bulk rheological properties of the firn near the surface.
Flow models of Colle Gnifetti in two and three dimensions were used to further validate the applicability of the flow law. Measured surface velocities, borehole tilt rates and ages of chemically dated layers are well reproduced by the model using standard values of the flow-law parameters A0 and n = 3. The firn-densification problem was calculated with the three-dimensional flow model, providing good agreement with the measured density profiles at all borehole locations.
Exceptional deformation rates were observed in the lowest 3 m of the borehole. These are attributable to flow irregularities caused by the unknown small-scale bedrock topography and the effect of special rheological properties of the ice near the base. Further investigations are required in situ and on core samples in order to determine the relative importance of these processes.
In this study we showed that accurate modeling of firn-covered cold glaciers can be achieved if the compressibility and the special rheological properties of firn, as well as the air-bubble close-off, are taken into account. Special emphasis should be given to the small-scale bedrock topography and reasonable boundary conditions at the model margins, which are critical for accurate flow models of such small, cold mountain glaciers.
Acknowledgements
This study builds on many results and discussions with S. Wagner. We thank G. Meyer for the radar equipment and his help during the fieldwork. We are greatly indebted to A. Iken who supported this study in all its stages and carefully read the manuscript. Special thanks are due to D. Wagenbach, L. Keck and R. Weisshaar for providing the opportunity to perform the borehole measurements and making preliminary results available to us. Many thanks to H. Gaggeler and M. Schwikowski for interesting discussions and unpublished data and to A. Daellenbach for preliminary results. We thank H. Rothlisberger for important literature hints, H. Rufli for his support in the field, and both for many amusing discourses. We also highly appreciate the collaboration with J. Meyssonnier and O. Gagliardini. The fieldwork under sometimes adverse conditions was supported by M. Wegmann, U. H. Fischer, G. Blasi, H. Boesch G. Kap-penberger, L. Keck, E. Kuriger, E. Plüss, S. Suter and R. Zergenyi. Many thanks are due to J. Luthiger and G. Senn for carefully manufacturing the mechanical and the electronic part of the equipment, to P. Rutschmann for adapting his code to our needs and to B. Nedela for the drawing. The helpful comments of two anonymous referees improved the clarity of the presentation. This project was funded by ETH research grant No 0–20–982–95.

















