1. List of Symbols
A Driving stress strength
B i Ice hardness (Pa s1/n )
D Sill depth scale (m)
f Buttressing parameter
G Basal drag strength
g (= 9.81) Gravitation acceleration (m s–2)
H Thickness scale (m)
h(x) Thickness (m)
h 0 Upstream thickness (m)
L Length scale (m)
m Basal flow-law exponent
n = 3 Ice flow-law exponent
r sw Non-dimensional sea-water density
t Time (s)
U Along-flow velocity scale (m s–1)
u Along-flow velocity component (m s–1)
u 0 Upstream velocity (m s–1)
x Along-flow coordinate (m)
δ/δx Longitudinal derivative (m–1)
ν Viscosity (Pa s)
ρ i (= 917) Density of ice (kgm–3)
τ b Dynamic basal drag scale (Pa)
2. Introduction
A local reversal in the surface slope of an ice sheet or ice stream is of interest both because slope reversal indicates anomalous basal conditions and because subglacial water flow is sensitive to the potential gradient provided by the ice/air surface slope.
Reversed ice/air surface slopes are observed in nature in the form of ice rumples on ice shelves (Reference Swithinbank and LucchittaSwithinbank and Lucchitta, 1986), lakes on the surface of the Greenland ice sheet and on the surface of Matanuska Glacier, Alaska, USA (Reference Alley, Lawson, Larson, Evenson and BakerAlley and others, 2003), and perhaps most importantly, on the down-glacier side of Vostok lake, Antarctica (Reference StudingerStudinger and others, 2003). Ice flowing over any localized reduction in basal lubrication or any bedrock high will tend to slow, thereby reducing the magnitude of the surface slope up-glacier of the obstacle or reversing that slope, and steepening the slope over the obstacle. Owing to the important role of longitudinal stresses over distances of less than a few ice thicknesses (Reference BuddBudd, 1970), there is no prohibition on local reversal of ice/air surface slope.
Here we examine the tendency to form such a slope reversal for an ice shelf grounding over a sill. We focus our efforts on the equilibrium profile of the ice flowing over a flat sill. This requires the simultaneous solution of the steady-state force and momentum balance. We next describe the model we use for this solution.
3. Model Description
The model equations used here are derived in detail in chapter 2 of Reference DupontDupont (2004), and the notation, listed above in section 1, is adopted from chapter 4 of Reference DupontDupont (2004). A brief derivation is included here as an Appendix. Our treatment of the force balance is similar to the one-dimensional approach of Reference Van der VeenVan der Veen (1986), and, although one-dimensional, is also similar in approach to the two-dimensional (plan-view) treatments found in Reference Morland, Van der Veen and OerlemansMorland (1987) for ice shelves, and appendix A of Reference MacAyealMacAyeal (1989) for ice streams and shelves. We adopt the geometry shown in schematic form in Figure 1 and the dimensional scales shown in Table 1. All variables are non-dimensional unless otherwise noted. The flow is from left to right, with x being designated the along-flow coordinate direction, and with the point x = 0 specified as the initial grounding point.
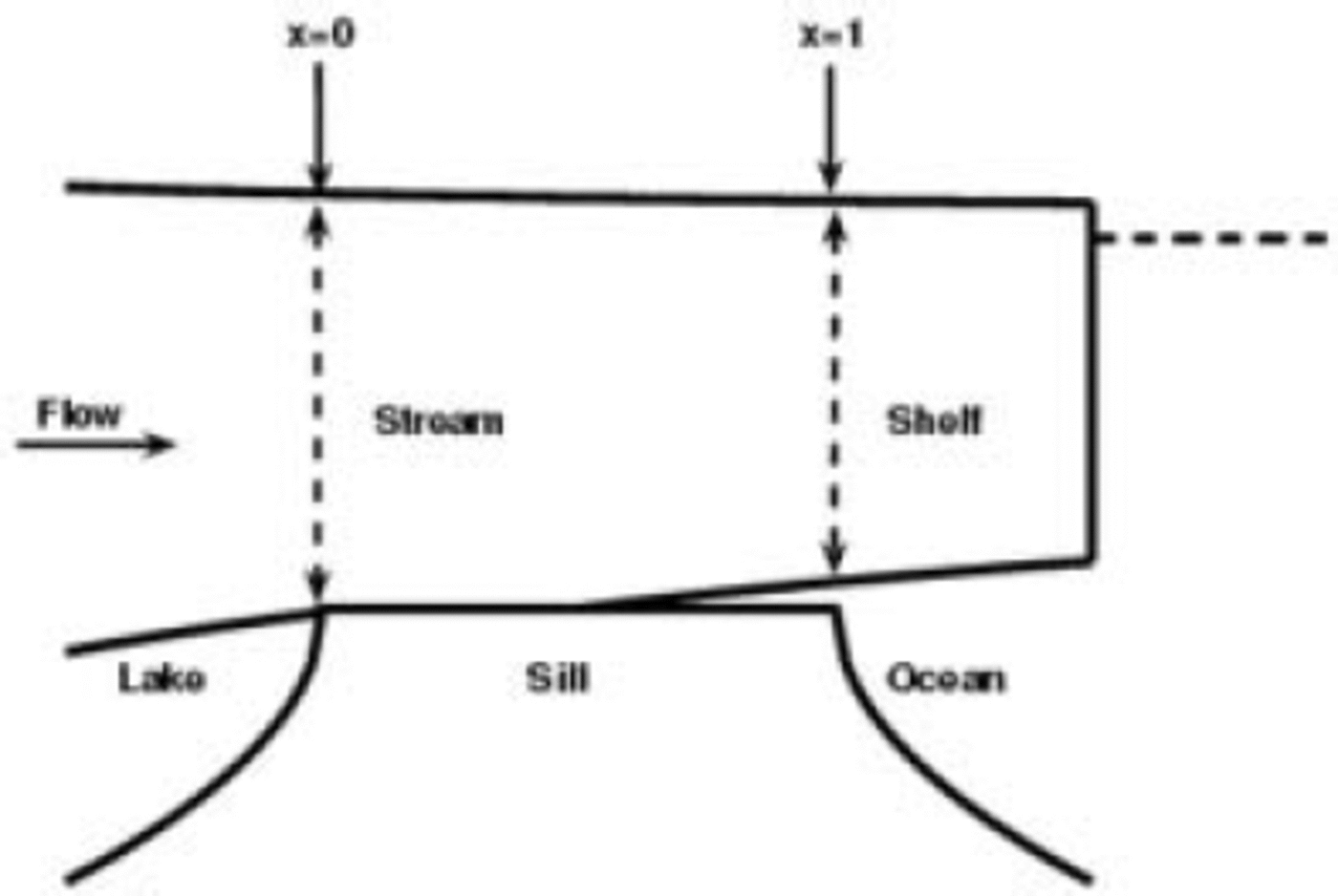
Fig. 1. Schematic geometry for the model problem. Flow is from left to right in the x direction. The domain extends from the upstream and downstream limits of the sill, at x = 0 and x = 1, respectively.
Table 1. Scales used to non-dimensionalize the force- and mass-balance equations along with their boundary conditions. The range of scales for A and G are those resulting from the full range of the scales on which these parameters depend

One scale of special note is the thickness scale H. For the present study we specify that this scale correspond to the flotation thickness for a sill depth of D given the ratio r sw of sea-water density to ice density, such that
This scaling implies that where the non-dimensional thickness is greater than unity the ice is grounded, and where the thickness is less than or equal to unity the ice is afloat.
3.1. Governing equations
If we neglect, primarily for the sake of simplicity, cross-flow variations in velocity and thus lateral drag, then the appropriate governing equation for the x-directed force balance is the depth-integrated Stokes equation, which in non-dimensional form is

where h is the thickness, u is the velocity and m is the exponent for basal friction. The effective viscosity ν is defined as

where n = 3 is the flow-law exponent for ice. The non-dimensional constants A and G measure the importance to ice flow of thickness gradients and basal drag, respectively. The values of A and G are determined by the choice of scales and parameter values according to the following definitions:


where ρ i is the density of ice, g is the acceleration due to gravity, H = r sw D is the thickness scale, B i is the ice hardness, U is the velocity scale, L is the length scale and τ b is the basal stress scale. Table 1 lists the values or range of values adopted for these scales and constants, as well as the resulting range of values for A and G.
There are two boundary conditions for the force balance.
The first is that we prescribe the velocity at the inlet (x = 0)
The second boundary condition is imposed at the terminal end (x = 1)

where f is an ice-shelf buttressing parameter and b(1) is the (undetermined) ice thickness at the terminal end of the domain. Equation (˚) is simply a linear combination of two reasonable end-members for the stress state at x = 1, with the weight we give each end-member being determined by the value we prescribe for f. The first end-member, found by imposing f = 0, is the usual ice-front condition, where the difference between the depth-integrated glaciostatic and hydrostatic pressures is balanced by a tensile depth-integrated longitudinal deviatoric stress, implying a positive longitudinal strain rate ∂u/∂x. This is the stress state one would expect at an ice front or at the junction with a freely floating ice shelf. The second end-member, found by setting f = 1, is a ‘fully buttressed’ condition, with zero depth-integrated deviatoric stress, resulting in zero longitudinal strain rate. The utility of f is that it allows for situations where the ice beyond x = 1 could be losing some momentum due to local grounding or perhaps lateral shear. In such a situation, the momentum flux that must be transmitted upstream (into the modeled domain) is reduced relative to the case of a free-floating ice shelf; we model this situation by setting f to something greater than zero.
Mass balance is governed by the evolution equation
where t is the non-dimensional time coordinate, and we neglect any source (or sink) of mass via accumulation (ablation). Equation (9), which is derived from mass continuity, simply states that the time rate of change in thickness is equal to the convergence of horizontal mass flux. At the upstream boundary (x = 0) we prescribe the thickness
Given that we are interested in scenarios where the ice is at least partially grounded as it flows across the sill, and given that we have defined the thickness scale such that h ≤ 1 implies flotation, we restrict the upstream thickness to being greater than unity
3.2. Numerical model and experiments
Our goal, given values for our poorly known parameters A, G, u 0, f and h 0, is to find out if the resulting equilibrium thickness distribution has a slope reversal. To find an equilibrium thickness distribution, we start at some initial guess for the thickness and let Equation (9) evolve toward steady state, subject to the boundary conditions (7), (˚) and (10), with the velocity given by Equation (3) at each instant in the evolution. Linear finite elements are used to discretize both Equations (3) and (9) in space. Equation (9) is discretized in time using semi-implicit finite differences, with a Petrov–Galerkin upwind-weighting scheme adopted in the spatial discretization to improve the stability and efficiency Reference Dupont(Dupont, 2004). An evenly spaced, 201-node mesh is used for the spatial discretization. In order to satisfy the strain-rate dependent viscosity and the force-balance equation (3) simultaneously, a simple substitution iteration is employed, usually requiring fewer than eight of these iterations to reach convergence within a given time-step. The numerical implementation of the force balance was tested against analytic solutions for steady-state ice shelves, with maximum errors less than 10–5. Implementation of the mass-balance component was checked using the analytic solution for an advected step function, showing maximum errors smaller than 10–4, as discussed in appendix B of Reference DupontDupont (2004).
4. Results and Discussion
We perform five sets of experiments, as outlined in Table 2. Within each set of experiments, we set the values for h 0, u 0, f and m and find equilibrium profiles for a range of A and G. For each profile we ask whether the profile has a surface slope reversal. We also ask whether the ice is grounded over the full extent of the domain, in which case we designate the profile as having ‘no shelf’, as it is fully grounded; otherwise the profile is designated as having a ‘partial shelf’, as the ice along some portion of the domain is floating.
Table 2. Sets of parameter values for the various numerical experiments. Note that the ranges for A and G adopted here fall within the broader range noted in Table 1

The results for the standard experiment are shown in Figure 2. There is clearly a transition from normal to reversed surface slope within the range of A and G chosen. The tendency is toward normal slope and partial grounding in the high-driving-stress, low-basal-drag portion of the space, and reversed slope and full grounding in the low-driving-stress-strength, high-basal-drag portion of the region. Two profiles are shown in Figure 2, as examples of the no-shelf (fully grounded), reversed surface-slope case and the partial-shelf, normal surface-slope case. Note that the other two possible cases, those of partially grounded, reversed surface-slope and fully grounded, normal-slope profiles, do in fact occur but occupy a smaller region of the parameter space explored.
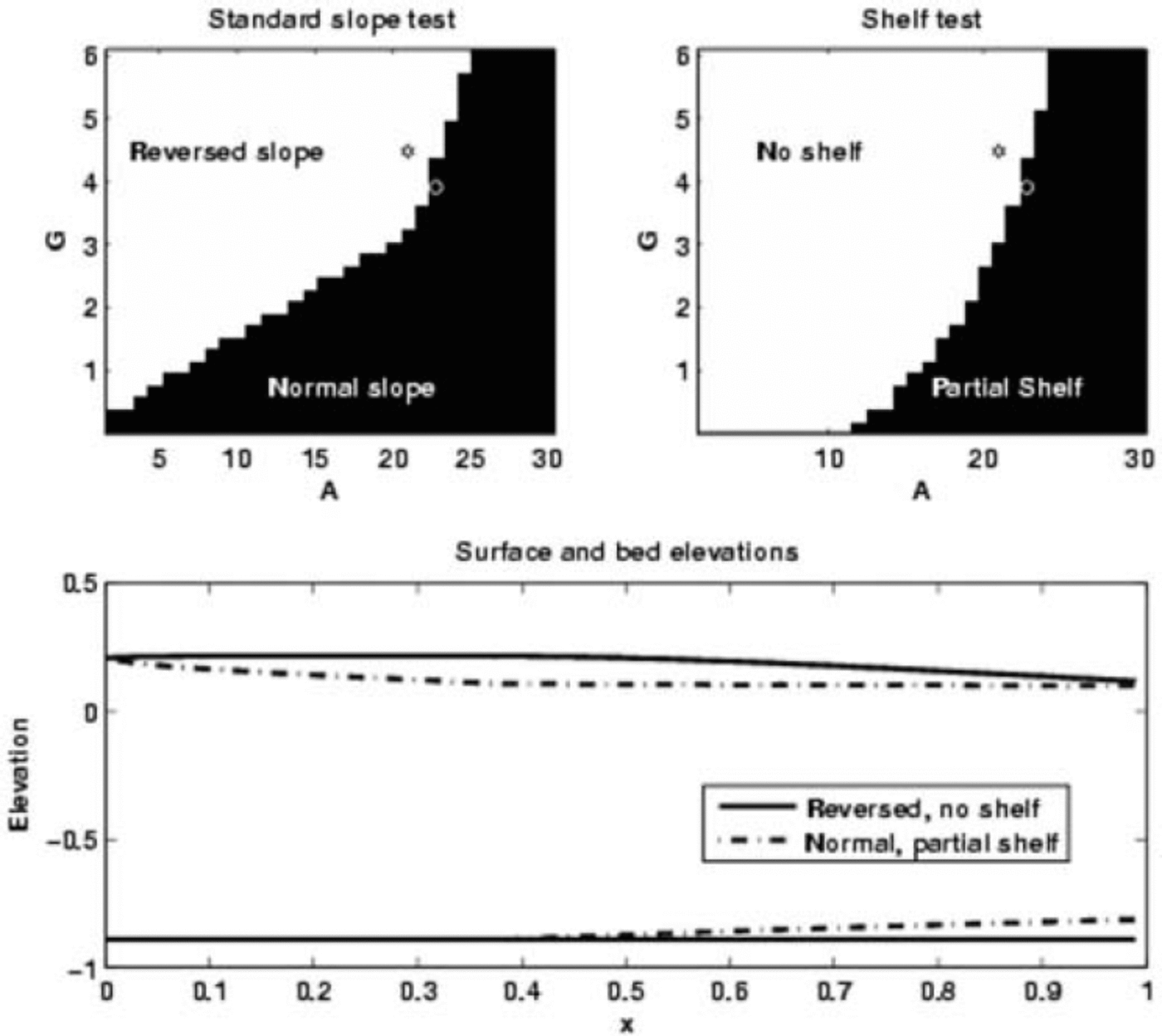
Fig. 2. Results of the standard experiment. The upper left panel shows the transition, in A–G space, from normal to reversed surface slope. The upper right panel shows the transition from profiles with no shelf (fully grounded) to those with a shelf on some portion of the domain. The lower panel shows the equilibrium surface and bed profiles for the two points in A–G space marked on the upper panels, chosen to exemplify profiles on either side of the transitions. The grounding point for the normal-slope, partial-shelf profile is at x = 0:38. For the reversed-slope, no-shelf profile, the slope changes sign at x = 0:21.
Figures 3 and 4show how perturbations in the standard set of parameter values affect the position, in A–G space, of the normal/reversed slope and no-shelf/partial-shelf transitions. The results of perturbing the bed rheology exponent (m) show essentially no difference from the standard
experiment. This is because it is the non-dimensional velocity u, which is always near unity, that the inverse of this exponent acts on in Equation (3). In effect, our non-dimensionalization precludes a strong response to variations in m. Because of this lack of sensitivity, we elect not to plot these results in the figures.
Decreasing the upstream thickness produces an expansion of the area of reversed surface slope for low driving stress and low basal drag. For higher driving stress and higher basal drag, decreasing the upstream thickness produces a contraction of the region of reversed surface slope. Thus, systems that are near the slope transition should be expected to seal (unseal) when low (high) in driving stress and basal drag and subjected to an upstream thinning. Similarly, upstream thinning produces an expansion of the partially grounded region in A–G space. This is expected in the sense that, as the ice thins upstream, the whole of the flow must thin, which will allow ice near flotation to reach flotation and unground. This ungrounding, for high driving stress and basal drag, leads to a transition to normal slope as the area over which basal drag operates is reduced.
Increasing the upstream velocity relative to the standard case produces an expansion of the reversed surface-slope and fully grounded regions of A–G. This is expected because higher velocity makes the profile become more advection-dominated. Similarly, introducing buttressing expands the reversed surface-slope and fully grounded regions. This follows from a weakening of the stretching required within the ice as buttressing is introduced at the downstream end.
5. Conclusions
From our exploration of parameter space, we see that the reversed surface-slope region invariably occupies the lower A, higher G portion of parameter space. Because these parameters are, respectively, directly and inversely proportional to the thickness scale, we see that thinning tends toward slope reversal. Similarly, making the bed stickier, as measured by G, tends toward slope reversal. Conversely, decreasing buttressing tends toward normal slopes. Thus we see that a transition to slope reversal is favored by thinning, strengthening the bed and increasing ice-shelf buttressing.
Given that the parameter values used in this study are well within reasonable glaciological values, we can say with confidence that we should expect slope reversals. To the extent that these slope reversals aid in trapping water within subglacial lakes, we can say that these results are at least consistent with outburst flooding, as described by Alley and others (in press).
Acknowledgements
This work was supported by US National Science Foundation grants OPP-0126187 and ESH-9814774. The manuscript benefited from discussions with B.R. Parizek, S. Anadakrishnan, M. Spencer, A. Huerta, R. Najjar, J. Kasting and D. Elsworth, as well as comments from J. Johnson and T. Hughes.
Appendix
Non-Dimensional Treatment
The goal of this appendix is to arrive at the non-dimensional forms of the depth-integrated force-balance equation and the terminal boundary condition (Equations (3) and (˚), respectively). Dimensional versions of the simplified force-balance equation and boundary condition will first be derived. Through the introduction of a non-dimensional mapping, these equations will be rendered into the forms used in the main body of the paper.
Force-balance equation
We begin with equation (1) of Reference MacAyealMacAyeal (1989), which is an x-directed momentum balance equation appropriate for ice streams and shelves. Using different notation, the dimensional equation is

where h is the ice thickness, z s is the ice/air surface elevation, x and y are the along-flow and cross-flow coordinates, u and v are the depth-averaged x- and y-directed velocities, ρ i is the density of ice, and g is the gravitational acceleration. τ b(u) is the basal friction. We assume the basal rheology follows a power-law form τ b(u) ≡ B b u1/m , where m is the basal flow-law exponent and B b is the basal friction coefficient.

Fig. 3. Effect of perturbations in upstream thickness (h 0), upstream velocity (u 0), and buttressing (f), on the position of the transition line from normal to reversed surface slope. The specific values of the perturbations to the various parameters are listed in Table 2. Note that the results of a perturbation in the basal rheology exponent (m) are not shown, as they are indistinguishable from the standard experiment.
ν is the depth-averaged effective viscosity

where B i is the ice hardness parameter and n is the flow-law exponent. The stress/strain-rate relation adopted here is σi ≡ 2ν ɛ ii , where i can be either x or y and the strain rate may accordingly be ɛ xx = ∂u/∂x or ɛ yy = ∂v/∂y, respectively.
For simplicity we now focus our efforts on wide, but confined, channelized flow, with negligible cross-flow velocity. This restriction allows the neglect of terms in Equations (A1) and (A2) involving the cross-flow velocity v and the cross-flow gradient ∂/∂y. We also restrict consideration to flow over a flat sill of depth D, such that grounded ice has a basal elevation z
b = –D, floating ice has a basal elevation of ![]() and the condition for flotation is h ≤ r
sw
D, where r
sw = ρ
sw
/ρ
i is the ratio of the density of sea water to that of ice.
and the condition for flotation is h ≤ r
sw
D, where r
sw = ρ
sw
/ρ
i is the ratio of the density of sea water to that of ice.
Adopting these simplifications and noting that the ice/air surface and basal elevations are related by z s = h + z b, the expressions for the force balance and viscosity, Equations (A1) and (A2), respectively, reduce to


Equations (A3) and (A4) are the dimensional forms of Equations (3) and (4).

Fig. 4. Effect of perturbations in upstream thickness (h 0), upstream velocity (u 0) and buttressing (f), on the position of the transition from a fully grounded (no-shelf) to partially grounded (partial-shelf) profile. The specific values of the perturbations to the various parameters are listed in Table 2. Note that the results of a perturbation in the basal rheology exponent (m) are not shown, as they are indistinguishable from the standard experiment.
Terminal boundary condition
Here we wish to derive a representation of the stress condition at the terminal end of the domain, where x = L. It is useful to note that the expression within the braces on the lefthand side of Equation (A4) is depth-integrated longitudinal stress
If the terminal end of the domain is an ice front, then at this point the depth-integrated longitudinal stress within the ice must balance the depth-integrated longitudinal stress provided by the sea water. Because sea water is effectively inviscid compared to ice, the depth-integrated longitudinal stress within the ocean is, to good approximation, the depth-integrated hydrostatic pressure. With sea level set to z = 0, the ice-front stress condition is then

This condition is also appropriate for the junction with a freely floating, laterally confined ice shelf. The condition implies a positive (stretching) depth-integrated longitudinal deviatoric stress, thus producing a longitudinal gradient in velocity at this point. We refer to this condition as unbuttressed.
An alternative to this unbuttressed, ice-front-like condition is one in which there is no longitudinal deviatoric stress. In this situation, the ice at the terminal end is buttressed by lateral or basal drag acting on ice downstream of x = L; for this fully buttressed case, the depth-integrated longitudinal stress is purely due to the depth-integrated glaciostatic pressure
Ideally, we would like to examine scenarios intermediate between these fully buttressed and unbuttressed cases. A simple way to accomplish this is through a linear combination of these two end-members

where f is the buttressing parameter, defined such that f = 1 and f = 0 imply a fully buttressed and unbuttressed condition, respectively. Equation (A5) is the dimensional form of Equation (˚).
Non-dimensionalization
To isolate key parameters we now introduce a non-dimensional mapping of the variables. The terms on the lefthand side of this map are dimensional variables. The terms on the right consist of the non-dimensional versions of these same variables, multiplied by a constant scale. The ice density, ρ i, gravitational acceleration, g, and the ice hardness, B i, are all treated as constants, thus requiring no non-dimensionalization.

where L, U and H are the scales for length, velocity and thickness, respectively. The scale for the basal drag, τ b, is introduced as concatenation of the arbitrary basal friction parameter B b and U 1/m . Note that the scale for the thickness is defined such that ice with a thickness of H is just at flotation over the sill of depth D.
Inserting this non-dimensional mapping into Equations (A3–A5), and doing a little algebra yields



where the parameters G and A result from division of the scales for basal drag and the longitudinal gradient in depth-integrated glaciostatic pressure, respectively, by the scale of the longitudinal gradient in the depth-integrated longitudinal deviatoric stress









