Introduction
Recently Reference BrownBrown (1981) proposed the use of jump equations for evaluating Shockwaves in snow. Normally Shockwave propagation is evaluated by seeking a direct solution to the governing equation of motion:
where T-ij is the stress tensor, p is the density, bj is the body force vector, and aj is the acceleration vector. If a proper constitutive law relating T-jj to the strain tensor εij is available, this equation can be substituted into Equation (1) and solved directly for the displacements.
Normally this method of solution is quite tedious, since the resulting equation is often nonlinear if the constitutive equation is nonlinear. Also, if large strains are involved, the wave equation becomes nonlinear by virtue of the kinematics involved. These types of equations can be solved numerically by the finite difference method. However, this method is sometimes complicated by stability problems. The particular problem of a pressure wave propagating through medium- to high-density snow (p>350 kg m−3) was solved (Reference BrownBrown 1980[b]). Large computation times were required since small time increments were required in order to avoid an unstable solution.
The problem of Shockwave propagation in low-density dry snow (100< p < 300 kg m−3) can be a complicated problem for several reasons. The material is much more compressible than high-density snow. This high degree of porosity allows a more complicated set of deformation mechanisms to take place during deformation. The resulting constitutive equation required to describe the material behavior is therefore more complicated. Due to the high porosity of low-density snow, the air wave which propagates through the pore space becomes more significant. Johnson (unpublished) indicates that effects of this wave cannot necessarily be neglected. Such effects further complicate the problem.
In the following sections, the problem of plane Shockwave propagation in low-density snow is studied. First a solution is presented to describe how a Shockwave propagates in snow when the effects of the air wave are neglected. A rate-sensitive constitutive law for low-density snow is used in this analysis. These results are compared with experimental results obtained by the author during a two-year test program. Finally, an analysis is presented for the case when the material is represented as a porous material made up of an ice structure with an air phase. In both of the above analyses, large-amplitude, plastic waves are studied.
Theory
We present here only a summary of the analytical formulation, since the formulation has been developed in detail earlier (Reference BrownBrown 1981). In that paper, the propagation of inelastic Shockwaves was developed in terms of jumps across the wave front. The wave front is treated as a singular surface propagating into an undisturbed medium. The wave produces jumps or discontinuities in pressure, density, particle velocity and other material parameters. Mathematically, the wave front is defined to be a smooth one-parameter family of points Y(t), such that Y(t) gives the position of the wave front at any time t. The wave velocity is
If f(X, t) is any material variable such as pressure or density, the jump or discontinuity produced across the wave is
where for any δ>0,
and
F− is the value of f just behind the wave front, and f+ is the value just ahead of the wave. Therefore, [f] represents the change in f due to the Shockwave. Normally Shockwave analysis is concerned with the evaluation of rates of change [p] and [p] as well as the actual calculation of [p] and [p].
A set of governing equations can be developed which describe the variation of [p] and [p] as the stress wave propagates through the snowpack. Rather than working with the density p, the density ratio a is used, where
pm being the density of the matrix material, in this case, ice. The governing equations used in this analysis are
v is the particle velocity, and the subscripts t and x imply the derivatives with respect to time and position, respectively. ![]() are, respectively the tangent, secant, and rate moduli behind the shockwave and are defined by the expressions
are, respectively the tangent, secant, and rate moduli behind the shockwave and are defined by the expressions
A superposed dot also implies time differentiation. It should be noted that [a] and [a]t are not the same expressions. [ȧ] represents the jump in ȧ, whereas [a]t is the rate of change of the jump [a], as indicated by Equation (9).
The three moduli are dependent upon the material properties and the wave amplitude. In the above, the pressure response p of the material was assumed to be rate dependent as well as dependent on α. In cases where p does not depend on α, E1 would vanish, and the above governing equation would simplify somewhat.
Material Properties
Since we are concerned here with plane waves, only a volumetric constitutive law relating pressure to density changes is needed. Snow is a rate-dependent material, although this dependency becomes less significant at higher rates of deformation. Brown (1980[b]) formulated a volumetric constitutive law for snow. This constitutive law was based on a granular geometric model which determines deformation in terms of pressure sintering. It has been shown to represent the volumetric properties of snow for large, high-rate compactions of snow. The constitutive law is
where
R, a0, Δ and L are the average values of grain radius, initial pore radius, neck radius and bond length. A, C, S0 are material constants for ice. C1, C2, C3 are constants which have the values of 1.12 × 10−2, 1.67, and 6.4 × 10−3. αQ and p0 are the initial values of the density ratio and density.
During deformation, the bond radius and bond length both vary, but the grain radius changes very little, since the grains are structurally much more rigid than the necks. Δ and L may be related to the snow structure and the pressure. These relations have proved to be cumbersome to use, and here an approximate relation is used to calculate these values. For Δ, the following expression is used:

This equation was found to approximate adequately the more complicated expressions used earlier (Reference BrownBrown 1980[b]).
The neck length L is found by solving the equation:
where

and
N represents the number of bonds per grain, and is seen to vary with density.
For a more detailed discussion of the constitutive law, the reader is referred to Brown (1980[b]). This constitutive law describes the behavior of snow for densities between 150 and 700 kg m−3 and for values of α ranging from -10−4 to as large as -105 s−1. In Equation (14), the last term is insignificant for values of |α| below 103 s−1. In the case of Shockwaves this term cannot be neglected.
Solution of Wave Problem
Equations (5) to (14) can be used to evaluate the manner in which the Shockwaves propagate through snowpack. In particular the decay rates [p]t, [α]t. and [α]|t are found and then integrated to evaluate their variation with time.
A finite difference solution is used, since the nonlinearities associated with the constitutive law preclude an exact solution, [α] and [α] are prescribed as the initial conditions. These two variables characterize the wave amplitude, [α] measures the jump in density due to the Shockwave, and [α] reflects the wave frequency in the sense that as [α] increases, the wave front becomes sharper with a higher rate of loading.
The solution technique will not be discussed in detail, since the procedure followed here is similar to that used by Brown (1980[a]). In that paper, only medium- to high-density snow was studied, since a different constitutive law was used. The study reported here allows a more detailed study of shock-wave propagation, since the constitutive law is defined in terms of micro-structural parameters such as bond geometry, grain size, etc. Consequently, this can provide some insight previously not available.
In implementing the finite difference method, density ratios α![]() at specific time points t‘ and coordinate positions xj are calculated by integrating the governing equations. It is assumed that p, v, ax, and a are all zero in front of the wave. Then the jumps [p], [v], [αx], and [α] equal, respectively, the values p, v−, αx, and α− behind the wave. Equations (9) (with f = α) and (10) can be put in the following difference forms (Reference BrownBrown 1981)
at specific time points t‘ and coordinate positions xj are calculated by integrating the governing equations. It is assumed that p, v, ax, and a are all zero in front of the wave. Then the jumps [p], [v], [αx], and [α] equal, respectively, the values p, v−, αx, and α− behind the wave. Equations (9) (with f = α) and (10) can be put in the following difference forms (Reference BrownBrown 1981)


Equation (23) and Equation (24) may then be used to solve directly for the rates of change [α]t and [α]t. In these equations the superscript implies the time t1 = t1-l + Δt, and the subscript implies the position Xj = Xj-1 + VJ_tΔt. The constitutive laws are used to evaluate the moduli in the above equations; Equation (8) is used to calculate the wave speed at each time, and Equation (7) is used to find the particle velocity. Equation (23) and Equation (24) are used to find new values of [α] and [α], i.e.
The difference between the procedure followed here and the one used earlier (Reference BrownBrown 1981) is that the constitutive law for this problem is much more complicated. The jumps in Δ, L, and N had to be calculated in order to evaluate the moduli ĒT, Ē s, and Ē1 just behind the wave. In order to do this, Equations (20) to (22) had to be utilized to find the respective jumps in Δ, L, and N.
The Shockwave solutions are shown in Figures 1 to 4, which are essentially parametric studies of attenuation rates for various snowpack properties. For instance, Figure 1 illustrates how density affects attenuation rates for waves which have the same initial pressure. Figures 2 and 3 compare the theoretical results with experimental results for two different density ranges. Figure 4 demonstrates how intergranular bonding affects Shockwave propagation. In this case, the average bond diameter was varied from 10% to as high as 40% of the average grain radius. Finally, Figure 5 illustrates the effect of initial value of the density ratio rate [α] on the rate of pressure attenuation [p]t.

Fig. 1. Effect of initial density on shockwave propagation in low-density snow.

Fig. 2. Comparison of experimental data with theoretical calculations.

Fig. 3. Comparison of experimental data with theoretical calculations.

Fig. 4. Effect of intergranular bonding on attenuation rates in low-density snow. Bonding is characterized by bond radius/grain radius ratio, Δ/R.
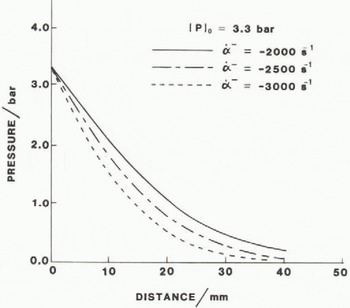
Fig. 5. Effect of wave frequency on attenuation rates Have frequency is roughly measured by the jump in & across the wave.
Snow as a Porous Medium
In the previous work by Brown (1980[a], 1981) the snowpack was treated as a continuous medium, and the interaction between the pore pressure and the ice structure was not evaluated. One of the few studies on snow which has considered the interaction between the air phase in the pores and the ice structure is that of Johnson (unpublished), who restricted his study to stress waves with the ice structure characterized as an elastic material. The air wave in the pores was found to be responsible for some of the dissipative processes observed in the acoustic waves studied.
Here we use a formulation similar to that of Reference Bowen and EringenBowen (1976). Again the wave is assumed to be a plane wave propagating in the X-direction such that the only macroscopically observable displacements are in the X-direction. This is a less general approach than Johnson’s study since his work involved more complicated displacement fields. Here we are concerned with intense plastic waves in which the material constitutive relations are quite complicated, and the simple geometry of plane waves will help to facilitate the analysis. Further, with plastic waves which produce pressures well in excess of 1 bar, the wave attenuation due to internal dissipation becomes the predominant factor characterizing this type of wave propagation, and this effect is adequately studied in the plane wave.
We now consider the snow to be made up of two materials, ice and air, which have respectively the partial stresses Пi, and Пa. These represent the portion of the actual pressure produced within the snowpack due to the Shockwave. In addition, we need to define momentum supplies ![]() i and
i and ![]() a for the ice and air which reflect the manner in which these two constituents interact with each other. The partial stresses and the momentum supplies are assumed to have the following forms:
a for the ice and air which reflect the manner in which these two constituents interact with each other. The partial stresses and the momentum supplies are assumed to have the following forms:

where va and Vi are the specific volumes for the two constituents. Va and ![]() ¡
are the material time derivatives of the specific volumes, i.e. they reflect the rate change of the specific volumes as each particular constituent motion is followed. During the shock loading each constituent will have different motions, and the material derivatives must follow each constituent motion. Therefore v
¡
are the material time derivatives of the specific volumes, i.e. they reflect the rate change of the specific volumes as each particular constituent motion is followed. During the shock loading each constituent will have different motions, and the material derivatives must follow each constituent motion. Therefore v ![]() a implies
a implies

Xa is the undeformed position of the air particle, xa is its time dependent deformed position, and ![]() a is the velocity of the air particle. Similar relations hold for the ice phase.
a is the velocity of the air particle. Similar relations hold for the ice phase.
Each phase, the ice and air, must satisfy mass balance and momentum balance postulates. These postulates for uniaxial motion in the x-direction are (Reference Bowen and EringenBowen 1976)


![]() a and
a and ![]() j are the accelerations, b is the body force, and vao and ViO are the initial values of specific volume in the undeformed configuration. Likewise pao and pio are initial densities.
j are the accelerations, b is the body force, and vao and ViO are the initial values of specific volume in the undeformed configuration. Likewise pao and pio are initial densities.
The momentum equations differ from the usual momentum balance equations in that the momentum supplies representing constituent interactions are now present. The mass-balance equations are the usual ones, since we assume mass exchanges due to phase changes are not significant. These governing equations may be solved in a manner identical to that used by Reference BrownBrown (1981) for Shockwaves in snow. Consequently the details of the solution will not be given here. The procedure results in the following set of equations governing the growth and decay of shock-waves:
where Fa = ∂xa/∂X, Fi = ∂xi/∂X are the deformation gradients



where ETia, E1ia. ETai, E1ai- are coupling tangent moduli and rate moduli

We see from Equation (30) and Equation (31) that the attenuation rates are affected by the momentum supplies and additional terms involving the coupling moduli. One can make a direct comparison between Equation (10) and Equation (30) and see that indeed differences do arise when the effect of the pore mass and its interaction with the ice structure are allowed. In fact, we end up with a set of coupled differential equations for the growth and decay of the shocks in both the ice and the pore mass.
Before a solution can be attempted, constitutive equations for the two phases are needed. They need to include terms which allow the calculation of the coupling moduli given in Equation (32). A possible form for the ice phase is:

and for the fluid or air phase
In the above, we take α = ρmvi, since the specific volume of the ice phase very closely approximates the value of 1/ρ for the snow. The above formulation assumes the same constitutive behavior as was used earlier for the ice phase, except the term Q(va/vao) is added to represent the coupling with the air phase. 0 is a coupling coefficient between the volume change of snow and the air. The fluid equation represents that of a gas plus the effect of coupling.
Finally the momentum supply would have to be of the form
where the coefficient A would be a function of α and vj. Then, with this assumed form,

With the use of Equation (28) and Equation (35) Equation (30) and Equation (31) become

and

In the above, the initial ice specific volume vio is just α0/ρm, where α0 is the initial density ratio ρm/ ρ0 for the snow, and ρm is the density of solid ice.
By comparing Equation (10) and Equation (39), the attenuation rate of the wave in the ice structure is augmented by the amount
The question about the order of these terms must then be considered. Based on previous work by the author and calculations by Johnson (unpublished), the following magnitudes may be attributed to the above terms in a Shockwave which produces a stress of 5 bar on the snow phase and a comparable pressure on the air phase

The above values for [vi]t, [vi,], and [vi,] were obtained from values calculated by Reference BrownBrown (1981). The following orders of magnitude result with the following equation:

If [va]t is of the same order as [v¡]t, the effect of Q[va]t/vao would be negligible. However, since [va] can be an order of magnitude larger than [vi], it appears reasonable that [va]t may exceed [vj]t by an order of magnitude. Therefore the effect of the air phase may actually become significant.
At the time of writing this paper, the author had no accurate values for the coefficient A. However, in order for this to be a significant factor, it would have to have a value with an order of magnitude of 105. In spite of this, it appears that coupling between the air and ice phases is large enough to increase attenuation rates appreciably. This would apply to the case of intense plastic waves which produce large partial stresses Пa in the air phase. With the current information available, a more definite quantitative statement cannot be made. More research into this problem is needed before the effect of the air phase on Shockwave propagation in snow can be determined quantitatively.
Discussions and Conclusions
The first part of this study was devoted to the propagation of nonsteady Shockwaves in low-density snow. The effect of the air phase in the pores was neglected. Only strong shocks producing massive compaction of the material were considered. The results of this analysis are illustrated in Figures 1 to 5. Some comparisons with experimental results obtained by the author is also presented in these figures.
Figure 1 gives a parametric illustration of the attenuation experienced as a function of propagation distance (X) and initial density. An initial pressure of 6.5 bar was used. A rather surprising result was that the Shockwaves in the higher-density snow attenuated more quickly. This appears to be characteristic only of inelastic Shockwaves which produce finite amounts of compaction. One explanation for this result is that the shocks traveled faster in the lower- than in the higher-density snow, since the former underwent much more compaction. Consequently, the low-density snow experienced more work-hardening. The resulting stiffening of the low-density snow due to this added compaction resulted with larger wave speeds.
Figures 2 and 3 compare data with theoretical calculations, and the results appear reasonable. Figure 4 illustrates how temperature gradient metamorphism can affect Shockwave attenuation. In this case attenuation for snow with three different bond radius/grain radius ratios were compared for snow. The initial shock pressures were adjusted so that the same density jump was initially produced in all three cases. Reduced intergranular bonding results with increased rates of Shockwave attenuation.
Finally, Figure 5 gives a qualitative measure of how wave frequency affects attenuation rates. Frequency here is roughly interpreted as proportional to the jump in the strain rate i due to the Shockwave. However, unless the shock structure is known, an exact correlation between the dominant wave frequency and the value of [a] cannot be specified in an exact manner. What can be said is that attenuation tends to increase with frequency.
The final part of the paper considered the wave propagation problem when the snow was modeled as a porous material with air filling the pores. The governing equations defining the attenuation rates of both the wave in the ice structure and the wave in the pore space were formulated. Since some of the constitutive coefficients describing the coupling effects between these two waves have not been accurately determined, the governing equations were not solved. However, an order of magnitude analysis did show that the interaction between the air and ice structures might significantly increase the attenuation rates. More work in this area is needed before a quantitative evaluation of this can be made.
Acknowledgment
The work reported in this paper was funded by US National Science Foundation (NSF) Grant No. CEE-7918050. The author wishes to express his appreciation to NSF for their support.







