1. Introduction
The satellite radar altimeter is an invaluable instrument for providing height measurements over ice sheets and ice shelves. The periodic monitoring of the polar regions using such measurements has long been proposed by the climate-change and glaciological communities (Reference RobinRobin, 1966). The first altimeter study on the Amery Ice Shelf, East Antarctica, was made by Reference Brooks, Williams, Ferrigno, Krabill, Oliver, James and JagoBrooks and others (1983) using Scasat data. They compared an altimeter-derived digital elevation model (DEM) with levelling data from a traverse made 9 years previously to look for evidence of elevation change over that period. A subsequent study looking for evidence of elevation changes in the Lambert Glacier-Amery Ice Shelf system employed orbit crossover analysis of Seasat and Gcosat altimeter data (Reference Lingle, Lee, Zwally and SeissLingle and others, 1994).
The internal consistency of altimeter height measurements can be determined by comparing surface heights along repeating tracks, and at exact crossover locations (Brooks and others, 1978). However, in order to assess the quality of the absolute height measurement and to determine flow well the altimeter height profile represents the true surface, an independently surveyed reference surface, referenced to the same ellipsoid and from the same epoch, is required. Such a surface can he obtained using kinematic-global positioning system (GPS) surveying techniques. This paper presents the results of a GPS survey carried out on the Amery Ice Shelf during the austral spring of 1995, designed to provide a height reference surface for the European remote-sensing satellite (ERS-1 and ERS-2) altimeters.
2. GPS Field Survey and Data Processing
The field programme took place on the Amery Ice Shelf between 25 October and 14 November 1995. A 120 km by 20 km grid, comprising twenty-four 10 km squares, was surveyed using kinematic GPS. The orientation of the survey grid is shown in Figure 1, together with the ground tracks of the 35 day repeal ERS orbits that cross it. Six base camps (C2-C12) were established along the centre line of the grid at 20 km spacing, starting at the southern end and moving north. The kinematic survey used two Leica 299 geodetic GPS receivers sampling at 5 second intervals, one serving as a local reference station at the base camps, the other mounted on a Skidoo which was driven around each of the four 10 km squares surrounding the base camps at approximately 10 km h . Static GPS data (30 s sampling) were collected from each base camp after the kinematic survey for the 2-3 day period for which it was occupied. For the entire duration of the survey, a fixed reference station was located on rock at Beaver Lake (a small tidal lake adjacent to the western edge of the ice shelf), using a third Leica 299 geodetic receiver observing at the same sampling intervals.
2.1. Static GPS processing and extraction of tidal signal
The multiple-day static GPS observations at each of the six Amery base camps were divided into approximately 2 hour segments. By combining each of these segments with data from the Beaver Lake site, Davis, Mawson and other Southern Hemisphere GPS tracking sites, a position was computed for each 2 hour segment using the Massachusetts Institute of Technology GPS analysis software GAMIT and GLOBK Reference King and BockKing and Bock, 1994). GAMIT uses coordinates at an epoch and enforces constraints on known coordinates. GLOBK combines GAMIT solutions, accounting for differences in a priori coordinates and allowing for constraining velocities to an a priori model. The 2 hourly averaged positions were calculated using a precise 3 day orbit for each camp, which overcame the discontinuities associated with short-span data in 24 hour segments. The movement was transformed into horizontal and vertical components tangential and normal to the surface of the World Geodetic System 1984 (WGS84) ellipsoid, which closely represent surface ice flow and vertical height variations, respectively.
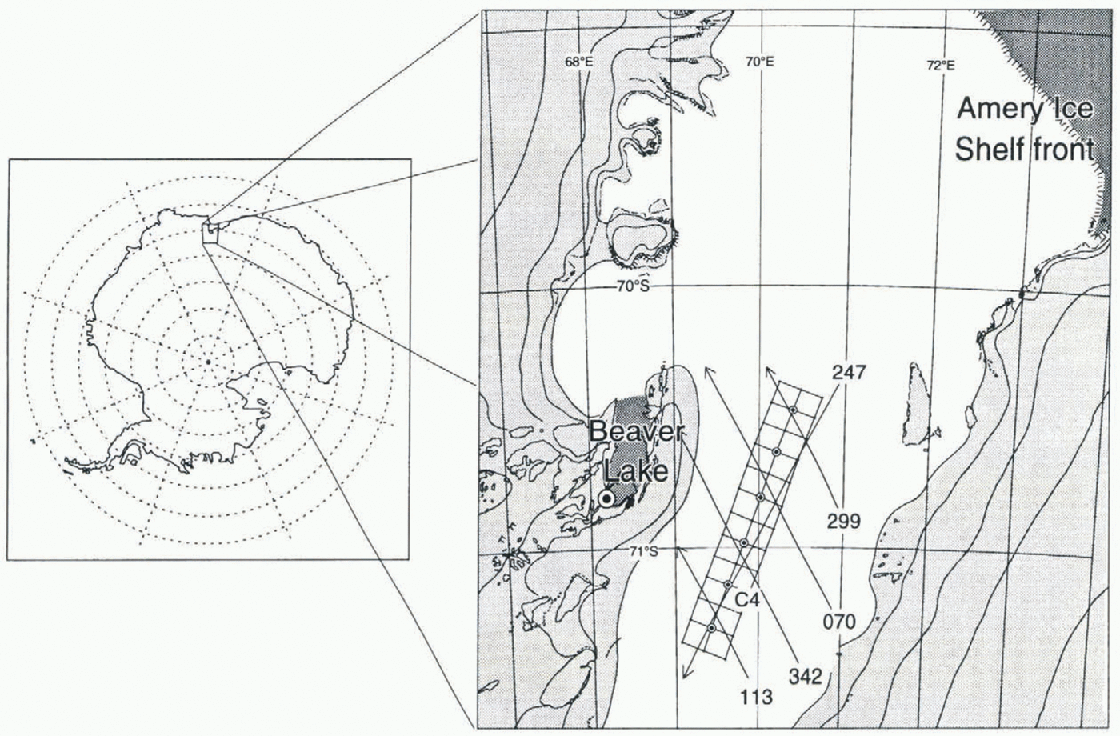
Fig. 1. Location of survey grid and ERS altimeter ground tracks on the Amery Ice Shelf The survey grid dimensions are 120 km × 20 km (adjacent grid nodes are 10 km apart). Base camps (C2-C12) were established at every second grid node along the centre line, and at Beaver Lake. Arrows on ERS tracks indicate the direction of satellite travel. Areas of no shading denote the approximate extent of the ice shelf light shading denotes grounded ice; and the darkest shading indicates open or ice-covered water.
A tide model, constructed from tide observations collected over a 22 day period during 1990-91, is available for Beaver Lake from the Australian National Tidal Facility.
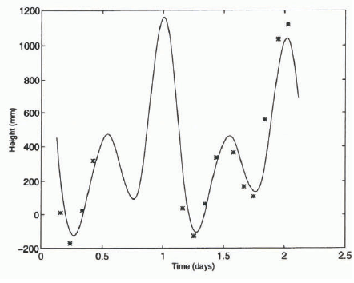
Fig. 2. Time series of the tide-induced vertical variation at the northernmost Amery base camp, computed at 2 hour intervals (stars), and the predicted tidefor Beaver Lake (solid line). A mean offset between the two time series has been removed.
Figure 2 shows the vertical-height variation at the northernmost Amery base camp, together with the predicted tide from the Beaver Lake model. This suggests that at this base camp the ice shelf responds hydrostatically, with little or no damping effects, to tidal forcing. in fact, the GPS vertical signal follows the tide values predicted by the Beaver Lake tide model to within 10-50 mm (Phillips and others, 1996). Only one of the six base camps (C4 in Fig. 1) did not display close similarities to the Beaver Lake tidal signal. This is most likely because the ice shelf is partially grounded (or sticking) at this point.
2.2. Kinematic GPS processing
The reduction of GPS kinematic data relies on having at least one known stationary point. There were two options for this survey: the Beaver Lake rock site or the Amery base camps. The first option provides the most stable station but has the disadvantage of having longer baselines (60-100 km), and hence uncertainties in resolving ambiguities. The base camps are in constant horizontal and vertical motion due to ice flow and tides, and differential processing with the rover unit on the Skidoo is problematical with con-ventional GPS processing software. To minimise these effects, the data were processed using both options, and the results combined. GAMIT was used for the static GPS processing, and Leica's Static Kinematic (SKI) software for the kinematic data.
With the base camps as the stationary points, only 2 out of 24 squares of kinematic data were processed completely; others could be processed only part-way round a square. Using the Beaver Lake site, 21 out of 24 squares were processed completely, although ambiguities were not resolved.
The GPS closure, i.e. the rms differences in the base-camp station coordinates between the start and finish of the survey, was approximately 0.4 m in all three components (latitude, longitude and height).
3. Altimeter data processing
The ERS altimeters have been operated with different orbital repeat periods: 3, 35 and 168 days. in this analysis we have used data from both the 35 day phase (October and November 1995) and the 168 day geodetic phase (April 1994-March 1995).
By using the 35 day data from the same time period as the field survey, we hope to have minimised any temporal height bias due to seasonal variations in penetration depth of the radar signal, resulting from changes in surface proper! ics of the ice shelf (Reference Ridley and PartingtonRidley and Partington, 1988). Figure I shows the five ERS satellite ground tracks from the 35 day-phase that cross the GPS survey grid. There are two repeat cycles of ERS-2 and one cycle of ERS-1 available from October and November 1995, all in ice mode.
The 168 day data provide a much denser spatial coverage over the survey region: 2-3 km between adjacent ground tracks, compared to approximately 30 km between adjacent tracks for the 35 day data. There are 48 ERS-1 satellite tracks from the geodetic phase that cross the GPS survey grid, all in ice mode.
There are a number of known biases and errors inherent in surface heights inferred from altimeter range measurements collected over an ice sheet or ice shelf. Those that have been corrected for in this analysis are listed below.
3.1. Merging of precise orbits
Highly precise orbits (relative to the WGS84 ellipsoid) produced with the Delft Gravity Model DGM-E04, based on satellite laser ranging, altimeter residuals and altimeter crossovers, were recently made available by the Delft University of Technology (Scharoo and others, in press). These orbits were used to update the spacecraft position. The radial precision of the Delft orbits is approximately 90 mm.
3.2. Retracking
The power received from each return altimeter echo is recorded as a waveform within a finite-width range window, quantised into 64 range bins of equal width (1.82 m in ice mode), with the leading edge corresponding to the initial interaction with the surface. The range measurement is made to the midpoint of the range window, and therefore, to obta in the true range, the distance to the leading edge-needs to be determined. The technique used to do this is the simple offset centre of gravity (OCOGJ algorithm, described byReference Wingham, Rapley and GriffithsWingham and others (1986). A percentage threshold value, determined by the total power under the waveform, is used to locate the retrack point on the leading edge. Retracking corrections in this analysis were made using the 10%, 25% and 50% threshold values.
3.3. Tidal correction
The ocean-tide values supplied in the altimeter records were derived from a model that is not valid over ice shelves. As previously mentioned, the GPS vertical height variation observed over the ice-shelf survey region closely matches that predicted by the Beaver Lake tide model, so this model was used to correct both the kinematic GPS data and the ERS altimeter data used for this analysis. All altimeter and GPS heights collected on the Amery Ice Shelf were referenced to the same datum (epoch-fixed), using the predicted tidal value for the observing epoch.
Table 1. Mean and rms of the height differences (m) at the intersecting points of the 35 day and 168 day ERS tracks and the GPS survey

The estimated error in the Beaver Lake tide model is about 10 mm (personal communication from M.Tait, 1996). The error in using the Beaver Lake tide model for the Amery Ice Shelf is approximately 50 mm (Phillips and others, 1996), based on GPS comparisons. There will, however, be a greater discrepancy in any regions of the ice shelf that are partially grounded (e.g. near base camp C4).
3.4. Atmospheric corrections
Mean atmospheric corrections were calculated (as in Reference CudlipCudlip and others, 1994) from in situ data: daily air pressure and temperature measured at the survey site; total integrated water-vapour values from atmospheric balloons launched at Davis and Mawson stations; and total electron-content shell from GPS data collected at Mawson station. The total combined correction (dry tropospheric, wel tropospheric and ionospheric) is 2270±15 mm. This compares with corrections supplied with the altimeter data of 2267 ± 25 mm for the 35 day dataset, and 2260 ± 28 mm for the 168 day dataset.

Fig. 3. Spatial distribution of height differences at intersecting points of 168 day ERS tracks and the GPS survey. The squares are scaled according to the magnitude of the rms height difference, with the inset square representing an rms error of 1 m.

Fig. 4. Surface heights generated from GPS data on a 0.5 km grid using kriging, with a combined spherical and exponential semi-variogram model. Units of the x and y axes are kilometres along and across the GPS survey, respectively (note the different scales). Units of the z axis are metres, greatly exaggerating the plot in this direction. The origin is in the southeast corner (71.43° S, 69.60° E).
3.5. Removal of quasi-specular returns
There were five waveform sequences in the 168 day data over the survey region that contained quasi-specular returns. This occurred when the altimeter passed over a recently refrozen meltstream, causing a strong reflection of the radar pulse back to the satellite (Phillips, 1998). The altimeter tended to lock on to these features, a problem known as snagging, leading to an erroneous range measurement. These returns were removed from the data.
4. Intercomparison of GPS and ERS Altimeter Data
There is a fundamental difference between the height measurements obtained by the two techniques under consideration. For the FLRS altimeters, it is a mean height for the whole pulse-limited footprint (approximately 2 km in diameter), whilst for GPS it is a height ofa single point in space. Three methods for intercomparison were used in this study.
4.1. Direct comparison at intersecting points
There are 83 intersecting points between the 35 day ERS tracks and the GPS survey; and 216 intersecting points between the 168 day ERS tracks and the GPS survey. Linear interpolation was used to obta in the altimeter-derived and GPS-derived height values at the exact point of intersection; only altimeter measurements separated along track by less than 600 m were used in the interpolation.

Fig. 5. ERS and GPS surface-height profiles along three of the five 35 day ERS tracks (070,113 and 247). The open squares represent ERS points, and the smaller solid squares the GPS surface height at each point.

Fig. 6. Surface heights generated from ERS-I altimeter data, on the same 0.5 km grid shown in Figure 4, using kriging with a different combined spherical and exponential semi-variogram model. Units of the x and y axes are kilometres along and across the GPS survey, respectively (note different scales), and units of the z axis are metres. The origin is in the southeast corner.
Table 1 shows the means and rms height différences at the intersecting points of the GPS survey and the ERS ground tracks, at the three retracking thresholds. Figure 3 illustrates the spatial distribution of these differences for the 168 day dataset at the 25% retracking threshold.
It can be seen from the above results that the 25% threshold produces the closest overall agreement with the GPS data, and that the height differences are greater in the southwestern region of the survey. Indeed, when only the intersecting points that lie in the northern part of the survey region (i.e. north of latitude 71°S) are considered, the rms height difference for the 168 day data at the 25% threshold is reduced to 0.9 m. The similarity of the statistics for the 35day and 168day datasets suggests that the temporal height bias over the Amery Ice Shelf is small during the time of the survey.
4.2. Comparison of surface-height profiles
To compare altimeter height profiles with the GPS data, a gridded reference surface over the surveyed region was created from the tide-corrected, kinematic GPS profiles. The technique chosen for the gridding was kriging, a geostatisti-cal technique that produces an optimal prediction of the surface at unobserved points (Cressic, 1993). in order to calculate the spatial variability of the data as accurately as possible, a combined (spherical and exponential) anisotropic semi-variogram was used. The directions chosen for the an-isotropy were oriented along the squares used for the GPS survey, and the variograms were computed using the GSLIBsoftware package (Reference Deutsch and JournelDeutsch andjournel, 1992).
The resulting gridded surface is illustrated in Figure 4. It can be seen from this plot that the survey covered a variety of topographic features. Towards the northern end of the survey, the topography is very smooth, whereas in the southern end two longitudinal depressions are revealed, approximately 3 km wide and about 5 m deep. These features are the refrozen meltstrcams previously mentioned, and described by Phillips (1998). The 35 day ERS data were not affected by snagging, because there was a layer of snow on top of the refrozen ice at the time of the overpass. For the comparison with altimeter heights, the grid resolution of the GPS height surface was decreased to 2 km, the approximate diameter of the altimeter pulse-limited footprint.
The resulting height profiles along three of the five 35 day ERS tracks (070,113 and 247) are shown in Figure 5. The profiles, using the 25% threshold, are plotted against distance in kilometres along the ground track, making the direction of satellite travel from left to right. Only one repeat of each ERS track has been shown, because the tracks repeal very closely. Track 070 has the least topographic variation, and the altimeter follows the surface reasonably well. The profiles along track 113, however, clearly illustrate the problems in using an altimeter to reproduce rough surfaces realistically. For example, the small, 3 m surface bump at 5 km is underestimated using the 25% threshold, and the 10 m rise at 20 km is detected as soon as it comes into the pulse-limited footprint. The longer, descending track 247 shows good agreement over most of the surface. The surface bump in the altimeter profile at 50 km is a real feature, but located to one side of the ground track and therefore not present in the sampled GPS profile.
4.3. Comparison of gridded surfaces
The 168 day ERS-1 altimeter data were gridded onto a 0.5 km grid using kriging. Similar to the gridding of the GPS data, a combined (spherical and exponential) anisotropic semi-variogram was again used, this time the directions chosen for the anisotropy being oriented along the altimeter tracks. Figure 6 illustrates the gridded surface obtained from the altimeter data. This surface is similar to thai generated from the GPS data (Fig. 4), but the altimeter surface is smoother and most of the features appear broader. This is to be expected, because the altimeter measures a mean surface height over the area of the pulse-limited footprint, and also tends to “see” high features early, as seen in track 113 (Fig. 5).
5. Contributions to Observed Height Differences
Differences between the ERS altimeter-derived heights and the GPS-derived heights can arise from a number of possible sources. The combined rms error remaining in the altimeter height measurements after merging in the precise orbits (~90mm) and correcting for propagation delays (~15mm) and tidal motion (~50mm) is ~104mm. The rms error introduced by the OCOG retracking method is 0.49 m per waveform in ice mode (Scott and others, 1994), which amounts to ~80 mm for the 35 day dataset (83 inter-sections), and ~50 mm for the 168 day dataset (216 intersections). The potential remaining sources of bias are:
Terrain bias: the shape of the altimeter waveform received by a radar altimeter is dependent on the properties of the surface with which the pulse interacts, and will be distorted to a varying degree, depending on inhomo-geneities on the surface. No simple retracker can account for these non-uniform waveforms, and techniques such as waveform migration (Wingham and others, 1993) are being developed to cope with this problem.
Surface layer penetration: this problem has been approached by Davis (1993) in his surface and volume retracking program, but has not been fully tested for ice mode, where there is a wider range window and the waveforms are more coarsely sampled. Surface penetration is of the order of 1 m on the Amery Ice Shelf, which introduces a height bias of about 10 cm (personal communication from J. Ridley, 1997).
6. Conclusions
It has been shown that the ERS altimeters can reproduce the surface topography ofan ice shelf, closely matching that obtained through ground survey, especially when the surface topography is smooth. At the 25% threshold in the OCOG algorithm, the mean and rms height differences at the intersecting points of the ERS-1 geodetic phase tracks with the GPS survey are 0.0 ± 0.1 m and 1.7 m, respectively. The spatial distribution of the height differences is highly correlated with the topographic variations evident in the gridded surface.
The total rms error remaining in the ERS altimeter height measurements, after merging in the precise orbits and correcting for propagation delays, tidal motion and tracking error, is at most 0.13 m. This error, combined with the GPS closure error of 0.4 m, does not fully account for the rms height difference of 1.7 m between the ERS and GPS heights. The only remaining sources of discrepancy are biases in the ERS heights arising from terrain effects and, to a lesser extent, surface layer penetration. An a priori knowledge of the surface topography would he required to extract more accurate height information from satellite alti-metry over ice regions.
This study has provided an accurate ground-truthing reference surface for the ERS altimeters, due to the large survey area and the high precision of the GPS coordinates. Data from the geodetic phase of ERS-1 are being used with in the Antarctic CRC to generate a high-resolution, accurate DEM of the Amery Ice Shelf. The reference surface will also be used, in conjunction with height measurements from future altimeter missions, to provide ongoing monitoring of elevation change on the Amery Ice Shelf.
Acknowledgements
The authors would like to thank: the Amery team members for the fieldwork (M. Craven, R. Manson, A. Ruddell, P. Johnson, S. Anglesey and P. Scholtz); the Australian National Tidal Facility at Flinders University, South Australia, for Beaver Lake tidal predictions; M. Craven for producing Figure 1; J. Ridley and R. Massoni for rev iewing early versions of the manuscript; R. Manson for her role in processing the GPS data; and X. Adams for supplying atmospheric data. The ERS radar altimeter data are copyright to the European Space Agency, 1991-96, and provided through AO project ERS.AO2.AUS103.









