1. Introduction
The history of the Earth over the past 65 Ma (the Cenozoic) is characterized by a general cooling trend from a ‘greenhouse’ to an ‘icehouse’ world (Reference Lear, Elderfield and WilsonLear and others, 2000). The variability in climate has increased considerably over time from a world with little continental ice prior to 34 Ma to an ice-dominated climate after this transition (e.g. Reference LiuLiu and others, 2009). This variability is strongly reflected in benthic deep-sea sediment records (Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others, 2001), which serve as a proxy for global ice volume and local deep-water temperature (e.g. Reference Chappell and ShackletonChappell and Shackleton, 1986; Reference Bintanja, van de Wal and OerlemansBintanja and others, 2005a).
In this study, both sea level and temperature over the second half of the Cenozoic era have been investigated with axisymmetrical one-dimensional (1-D) ice-sheet models (Reference Wilschut, Bintanja and van de WalWilschut and others, 2006) simulating glaciations on both hemispheres using benthic δ18O as model forcing. The continental mean surface-air temperature for the Northern Hemisphere (NH) has been reconstructed with an inventive inverse procedure. This procedure linearly relates the NH temperature to the difference between the modelled and observed benthic δ18O 100 years later (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2005a). As a result, a mutually consistent and continuous record of benthic δ18O, sea level and temperature has been obtained over the past 35 Ma with a 0.1 ka resolution. Moreover, the sea-level record has been derived from ice-volume fluctuations representative of all significant continental ice sheets that existed during the past 35 Ma.
Simulations have been performed with five hypothetical ice sheets: in the NH, two contintental ice sheets represent glaciation on the Eurasian (EAS) and North American (NAM) continents, respectively, and another ice sheet simulates the Greenland ice sheet (GIS). Antarctic glaciation has been simulated with two separate ice sheets. This separation was included to create a more climate-sensitive West Antarctic ice sheet (WAIS), i.e. to make it more responsive to temperature and sea-level fluctuations than the East Antarctic ice sheet (EAIS). Furthermore, key processes for simulating ice-sheet evolution have been included in the model such as the feedback mechanisms between mass balance and albedo and between surface height and surface mass balance, as well as adjustment for the underlying bedrock.
2. Model Formulation
The model is an axisymmetrical 1-D ice-sheet model that simulates ice flow over an initially cone-shaped ‘continent’, i.e. with a constant negative bedrock slope in the radial direction (values and constants are listed in Tables 1 and 2, respectively). The input for the model is benthic δ18Oobs data (Reference Lisiecki and RaymoLisiecki and Raymo, 2005; Reference Zachos, Deickens and ZeebeZachos and others, 2008) that are used to derive the continental mean NH temperature with an inverse procedure (observation-constrained forward modelling), linearly relating the temperature relative to the present day, (PD), ΔT, to the difference between the modelled and observed benthic δ18O 100years later (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2005a):
where ![]() is the mean NH temperature (°C) of the preceding (pm) 1000 years and c represents the temperature response with respect to changes in the observed δ18Oobs record, per 100 years (Table 2). These values were determined by minimizing the difference between modelled and observed δ18O, i.e. the observed δ18Oobs record must be accurately followed.
is the mean NH temperature (°C) of the preceding (pm) 1000 years and c represents the temperature response with respect to changes in the observed δ18Oobs record, per 100 years (Table 2). These values were determined by minimizing the difference between modelled and observed δ18O, i.e. the observed δ18Oobs record must be accurately followed.
Table 1. Model parameters for the five ice sheets

Table 2. Constants used in the model; values are adopted from Reference Wilschut, Bintanja and van de WalWilschut and others (2006) except for the tuning parameters used in Equation (1) Tuning parameter.

The derived NH temperature was used to run the ice-sheet model in forward mode over 100 years, as shown in Figure 1. The temperature anomaly is used in two procedures: the ice-sheet model (left) and the evaluation of the deep-water temperature anomaly ΔT o (right). Within the ice-sheet model, the isotopic content and ice volume are calculated with a time-step of 1 month and are fed into the ocean isotope module. Global sea level relative to PD is internally calculated from all ice volumes. After each output time-step of 100 years, the modelled benthic isotope (δ18Ob, Equation (2)) is evaluated and forwarded to the inverse method to calculate the temperature anomaly for the next time-step.

Fig. 1. The continental mean NH surface-air temperature anomaly from present day, ΔT, is calculated every 100 years using the inverse routine described by Equation (1).
The inverse method is based on the fact that the two dominant contributions to the benthic δ18Ob signal, i.e. ice volume and deep-water temperature, are closely related to the mid-latitude-to-subpolar NH temperature, which controls the waxing and waning of the EAS and NAM ice sheets (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2005a). The derived surface-air temperature anomaly ΔT is therefore representative of both continents and can be directly applied to the EAS and NAM ice-sheet models.
To apply the temperature anomaly ΔT to the Antarctic and Greenland ice sheets, however, a temperature difference from EAS/NAM ice sheets needs to be derived. This temperature difference between the continents can be interpreted as a combination of two components: the different geographical location (i.e. a higher latitude leads to lower temperatures) and the presence of an ice sheet which lowers temperatures through feedbacks to the local climate.
The differences for the PD climate were determined by calculating the continental mean temperatures from the Climate Prediction Center dataset (1948–2008; Reference Fan and Van den DoolFan and Van den Dool, 2008) for Antarctica and from the Climate Research Unit TS3 0.5˚ dataset (1901–2006; Reference Brohan, Kennedy, Harris, Tett and JonesBrohan and others, 2006) elsewhere. Temperatures were reduced to sea level using the PRISM (Parameter elevation Regressions on Independent Slopes Model) dataset (Reference Edwards, Kineman and OhrenschallEdwards, 1992) with a lapse rate of 6.5˚C km−1, equivalent to the lapse rate used in the models.
The geographically induced differences from the NH continental mean temperature, δT NH, can be directly applied to the surface temperature calculated from the inverse routine ΔT and are listed in Table 1 . The choice of δT NH is a subject for discussion, and the sensitivity of the model to different values of δT NH is tested in section 3.4. For both the EAIS and GIS, however, δT NH has been used to tune the volume changes to a strong volume increase of the EAIS around the Eocene–Oligocene boundary (Reference DeConto and PollardDeConto and Pollard, 2003) and to a simultaneous initiation of the GIS with the large NH ice sheets, respectively. For the latter, the initiation of NH glaciation (and especially initiation of the GIS) is still under discussion (e.g. Reference Bartoli, Sarnthein, Weinelt, Erlenkeuser, Garbe-Schönberg and LeaBartoli and others, 2005), but most evidence points to an initiation around 3 Ma bp (e.g. Reference WhitmanWhitman, 1992; Reference Sato and KameoSato and Kameo, 1996).
The feedback mechanism between ice sheet and climate is less straightforward and has been tested as a parameterization dependent upon the ice-sheet radius. The model outcome including this parameterization, however, did not show any large differences from the original results. We therefore excluded an additional correction to temperature in order to keep the interpretation of sea-level and temperature variations as transparent as possible.
2.1. Including stable oxygen isotopes
The benthic δ18Oobs data used as input for the model originate from the calcite shell of benthic foraminifera and serve as a proxy for global ice volume and local deep-water temperature (Reference Chappell and ShackletonChappell and Shackleton, 1986). The δ notation represents the ratio relative to the Vienna 18O/16O Pee Dee Belemnite (VPDB) standard. To separate the two signals we used an equation for the modelled benthic δ18Ob value based on mass conservation of δ18O in ice and ocean water (see Appendix):

where Viand V
o represent the ice-sheet and ocean volume in metres sea level equivalent (m s.e.), respectively, and ![]() is the mean oxygen isotope content of the ice sheets (‰). Listed in Table 1 are the PD values of equivalent sea level (adopted from Reference Bintanja, van de Wal and OerlemansBintanja and others, 2002) and
is the mean oxygen isotope content of the ice sheets (‰). Listed in Table 1 are the PD values of equivalent sea level (adopted from Reference Bintanja, van de Wal and OerlemansBintanja and others, 2002) and ![]() (from Reference Lhomme, Clarke and RitzLhomme and others, 2005). For the isotope content of the ice sheet, δ18Oi, we use the formulation introduced by Reference CuffeyCuffey (2000):
(from Reference Lhomme, Clarke and RitzLhomme and others, 2005). For the isotope content of the ice sheet, δ18Oi, we use the formulation introduced by Reference CuffeyCuffey (2000):
where δ18OPD (‰) is the PD distribution over the ice sheet as a function of the mean annual temperature, corrected for surface elevation T ma (°C). For the GIS we adopted the relation derived by Reference Zwally and GiovinettoZwally and Giovinetto (1997):
which is also applied to the EAS and NAM ice sheets. Although we cannot constrain the isotopic depletion of the EAS and NAM ice sheets, the δ18Oi will most probably be close to (but slightly higher than) that of the GIS. This difference, however, is included due to the applied temperature difference 5 TNH between Greenland and NAM/EAS. For the EAIS and WAIS, we used a different equation adopted from a similar study for Antarctica:
(Reference Giovinetto and ZwallyGiovinetto and Zwally, 1997). The additional terms in Equation (3) relate δ18Oi to changes in temperature (°C) and surface elevation (km) with respect to PD. Values for the isotopic parameters βT and βZ are listed in Table 1 and selected within the range presented by Reference Lhomme, Clarke and RitzLhomme and others (2005).
The last term on the right-hand side of Equation (2) represents the contribution of the ocean deep-water temperature ΔTo (°C), where y = −0.28.‰°C−1 (Reference Duplessy, Labeyrie and WaelbroeckDuplessy and others, 2002). To calculate the deep-water temperature we adopted a parameterization used by Reference Bintanja, van de Wal and OerlemansBintanja and others (2005a), for which the deep-water temperature ΔTo is linearly related to the 3 ka mean NH temperature ΔT (˚C):
In this way, ΔTo can be seen as an NH mean (similar to ΔT) deep-water temperature anomaly relative to PD. The 3 ka time lag can be qualitatively understood from the response timescales of the ocean with respect to the atmosphere (the former has a timescale of several ka; the latter a few months). According to Reference Bintanja, van de Wal and OerlemansBintanja and others (2005a), longterm variations in deep-water and surface temperatures show sufficient coherence to justify the use of this relationship. Furthermore, the processes involved (e.g. vertical mixing and deep-water formation) are far too complex to include in our simplified modelling study.
The coupling coefficient Adw was determined using a simplified atmosphere-ocean climate model (Reference Bintanja and OerlemansBintanja and Oerlemans, 1996) by correlating atmosphere to deep-water temperatures in a series of transient climate runs. In Reference Bintanja, van de Wal and OerlemansBintanja and others (2005a), Adw = 0.20 (denoted by a in the supplementary information of Reference Bintanja and Van de WalBintanja and Van de Wal, 2008). This value is also adopted for the NH-only experiment. In contrast, for the full model a slightly lower value of Adw = 0.15 was used. This resulted in a lower reconstructed sea level during the Pleistocene with respect to the latter value, and better agreement with observed sea-level variations. A more thorough discussion of model sensitivity to this parameter is included in section 3.4.
2.2. Ice-sheet height and bedrock adjustment
The 1-D ice-sheet model is applied along a flowline on an equally spaced grid, although the number of gridpoints and the grid spacing is different for each ice sheet (shown in Table 1). The height of the ice sheet H and the bedrock elevation b (in m) are explicitly calculated on each gridpoint with a time-step of 1 month. The rate of change of the ice-sheet height is given by the continuity equation (Reference Van der VeenVan der Veen, 1999; Reference Wilschut, Bintanja and van de WalWilschut and others, 2006):
where U is the mean horizontal velocity (ms−1), B is the local surface mass balance (ma−1) and r is the distance from the centre (m). The mean horizontal velocity consists of a deformation velocity, which results from driving stresses and is based on the shallow-ice approximation, and a Weertman-type sliding velocity representing velocities at the bed (Reference Van der VeenVan der Veen, 1999):
where f d (Pa−3s−1) is the deformation and fs (Pa−3 m2s−1) is the sliding parameter, listed in Table 2. The driving stress Td (kgm−1 s−2) is proportional to the ice thickness H and the slope of the ice surface. n = 3 is the exponent in Glen’s flow law.
The adjustment of the bedrock to the ice load is based on the principle of local isostatic equilibrium (Reference Van der VeenVan der Veen, 1999) and is given by:

where Tb is the relaxation time of the asthenosphere in years and k is the ratio of the density of ice and the underlying bedrock material, listed in Table 2. The initial state of the bedrock is given by b0 = H b c – (db/dx)x, where H bc is the central bedrock height (m) and db/dx is the slope of bedrock, as listed in Table 1.
The choice of these parameters is critical for the model results; changing the bedrock slope has a significant impact on both temperature and sea level. As a second tuning target in the model, these two parameters were chosen such that the simulated NH ice volume at the Last Glacial Maximum (LGM, around 20 ka) is close to the generally established sea-level drop of 120 ± 10m (e.g. Reference RohlingRohling and others, 2009). For the Antarctic and Greenland ice sheets, the values were chosen such that ice volume (ms.e.) at PD is close to the PD value shown in Table 1.
2.3. Mass balance
The mass-balance parameterization is an important aspect of an ice-sheet model and serves as the coupling between temperature and ice volume. Both mass-balance components (accumulation and ablation) are calculated explicitly for each gridpoint. The ablation rate A (ma−1) is a function of temperature and solar insolation, and is based on PD mass-balance observations and modelling results for Antarctica and Greenland (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2002):
where Q is the monthly mean incoming shortwave radiation at the top of the atmosphere (Wm−2) which varies over time (Reference Laskar, Robutel, Joutel, Gastineau, Correia and LevrardLaskar and others, 2004). For each ice sheet, a different latitude was used to calculate the monthly mean values: 65˚N for EAS and NAM; 70˚N for GIS; and 80˚S for EAIS and WAIS. The constant C abl indicates a certain threshold value for ablation to begin, depending on temperature and insolation. For the two NH ice sheets, C abl = –28. This balances the PD yearly mean insolation, requiring ablation to be non-zero for temperatures above freezing.
Values for Greenland and Antarctica were based on their PD temperature differences as discussed in section 2, resulting in C a b l = –48, –76 and –90 for GIS, WAIS and EAIS, respectively. Although these are slightly different from the values determined by Reference Bintanja, van de Wal and OerlemansBintanja and others (2002), they have been selected for as much consistency as possible in the model. The temperature Tms (˚C) is the mean surface-air temperature corrected for height with a lapse rate of –6.5˚Ckm–1 and for seasonality by a superimposed sine function. The surface albedo α is defined:
where α g, α sn and α su are the soil, snow and surface (soil or ice) albedo, respectively (listed in Table 2), d is the snow depth (m) and A is the ablation rate at the previous time-step, calculated from Equation (8). The e-folding term represents the effect of snow thickness and patchiness on the albedo, with the snow depth determined within the model as a function of the cumulative mass balance (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2005b).
Accumulation is determined using temperature and ice-sheet extent. Firstly, temperature influences the moisture content of the atmosphere, i.e. higher temperatures lead to higher humidity and thus relatively more precipitation. This relation is taken into account by means of an exponential dependence on temperature T ms (˚C), based on the Clausius–Clapeyron relation. Secondly, a bigger ice sheet prohibits the deposition of snow on the ice sheet. This is taken into account by relating the precipitation to an e-folding critical radius (Reference OerlemansOerlemans, 2004a), approximately the maximum extent of the ice sheet:
where P 0 (m a−1) is the uncorrected precipitation constant, R is the radius of the ice sheet and R c the critical radius (km) (Table 1).
Finally, monthly snow accumulation is obtained as a temperature-dependent fraction of precipitation (Reference Bintanja, van de Wal and OerlemansBintanja and others, 2002). The values of P 0 represent ice-sheet climate sensitivity, based on PD observational data, and are chosen such that: (1) the NH is wetter than Antarctica; (2) the WAIS is more sensitive than the EAIS; and (3) the NAM ice sheet is more sensitive than the EAS ice sheet.
3. Results
3.1. Validation for the Northern Hemisphere
Firstly, to support the 35 Ma simulations presented below, the outcome of the simplified 1-D ice-sheet model was compared to previous simulations conducted using a comprehensive three-dimensional (3-D) ice-sheet model (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008). Similar to the 3-D model experiment, we performed simulations over the past 4Ma with the EAS and NAM ice sheets only, forced with the LR04 global stack of 57 benthic δ18O records (Reference Lisiecki and RaymoLisiecki and Raymo, 2005), linearly interpolated to a 100 year resolution. Moreover, we assumed that the NH ice sheets contributed to 85% of global sea level and 95% of benthic isotope variations, in agreement with the assumptions made by Reference Bintanja, van de Wal and OerlemansBintanja and others (2005a). These two corrections were applied to Equations (A5) and (2), respectively.
Over the past 3 Ma, the results for NH glaciation simulations with the 1-D model are similar to the 3-D model results (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008), as can be seen in Figure 2. On average, the absolute differences are 1.0˚C for NH temperature and 6.2 m for sea level. The difference (root-mean-square) between modelled and observed benthic δ18O is very small and less than 0.005‰. Furthermore, the orbital frequencies present in the benthic isotope signal (see Reference Lisiecki and RaymoLisiecki and Raymo, 2007) are reproduced by temperature and ice volume. This is illustrated for temperature in Figure 3, which clearly shows the shift from the 41 ka world to the 100 ka glacial cycles of the late Pleistocene.
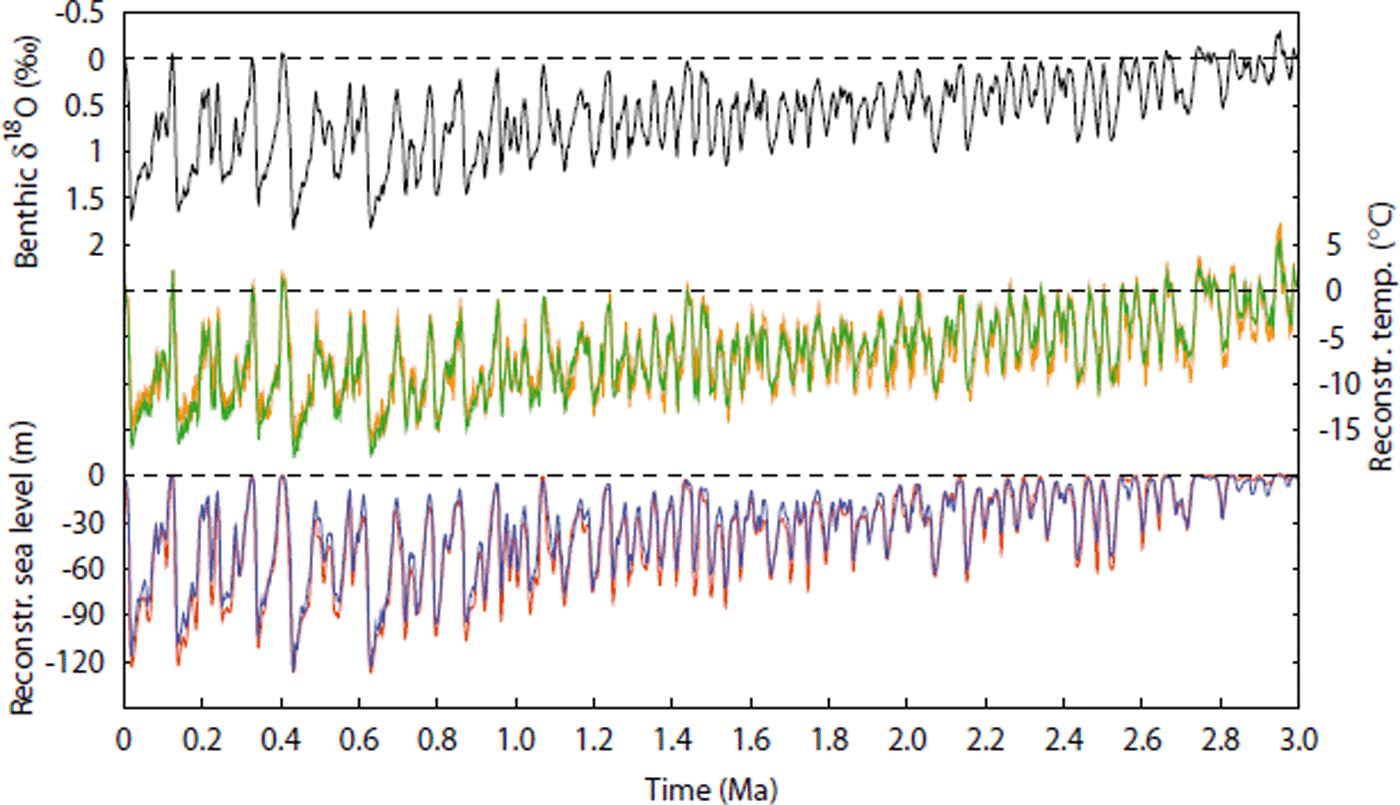
Fig. 2. Reconstructions over the past 3 Ma. From top to bottom, the LR04 (Reference Lisiecki and RaymoLisiecki and Raymo, 2005) global stack of benthic δ1 8O in black; 1-D model reconstructed NH temperature in green; and global sea level in blue. The 3-D model results (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008) are shown in orange for temperature and in red for sea level. All values are relative to PD.
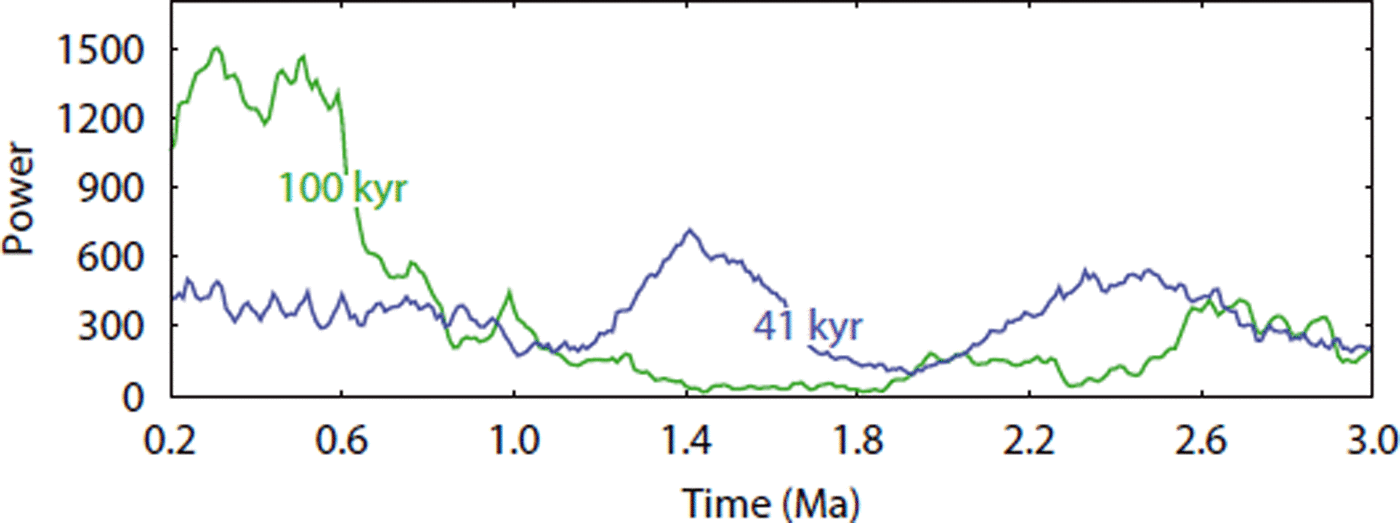
Fig. 3. Change of the 100 ka (green) and 41 ka (blue) frequency power of reconstructed NH temperature over the past 3 Ma. We applied a Blackman–Tukey spectral analysis with a Parzen window, 95% confidence limits and 3600 lags (90% of the data) to a moving window of 400 ka shifting with 10 ka (361 data points in total). Analysis was conducted using the AnalySeries program (version 2.0.3; Reference Paillard, Labeyrie and YiouPaillard and others, 1996).
Generally, temperatures in the 1-D model are higher than in the 3-D model. The timing of maxima and minima agrees well with the 3-D model, also supported by the similarity of the power spectra (not shown). Sea-level differences are relatively smaller, although ice-sheet growth is initiated at a few degrees above PD. This is in contrast to the 3-D model (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008), for which a threshold of –5˚C was observed. As already pointed out by Reference Wilschut, Bintanja and van de WalWilschut and others (2006), the simplified geometry of the 1-D model is the major cause of the dissimilarities between the two models.
3.2. A 35 Ma record of sea level and temperature
For the complete simulation including ice sheets in both hemispheres we used the updated composite benthic δ18O dataset of Reference Zachos, Deickens and ZeebeZachos and others (2008), shown in Figure 4a, smoothed over eight data points and linearly interpolated to 100year resolution. As can be seen in Figure 4b and c showing reconstructed sea level (blue) and temperature (green), respectively, both variables closely follow the pattern of the δ18O record as for the NH-only experiment discussed in section 3.1.
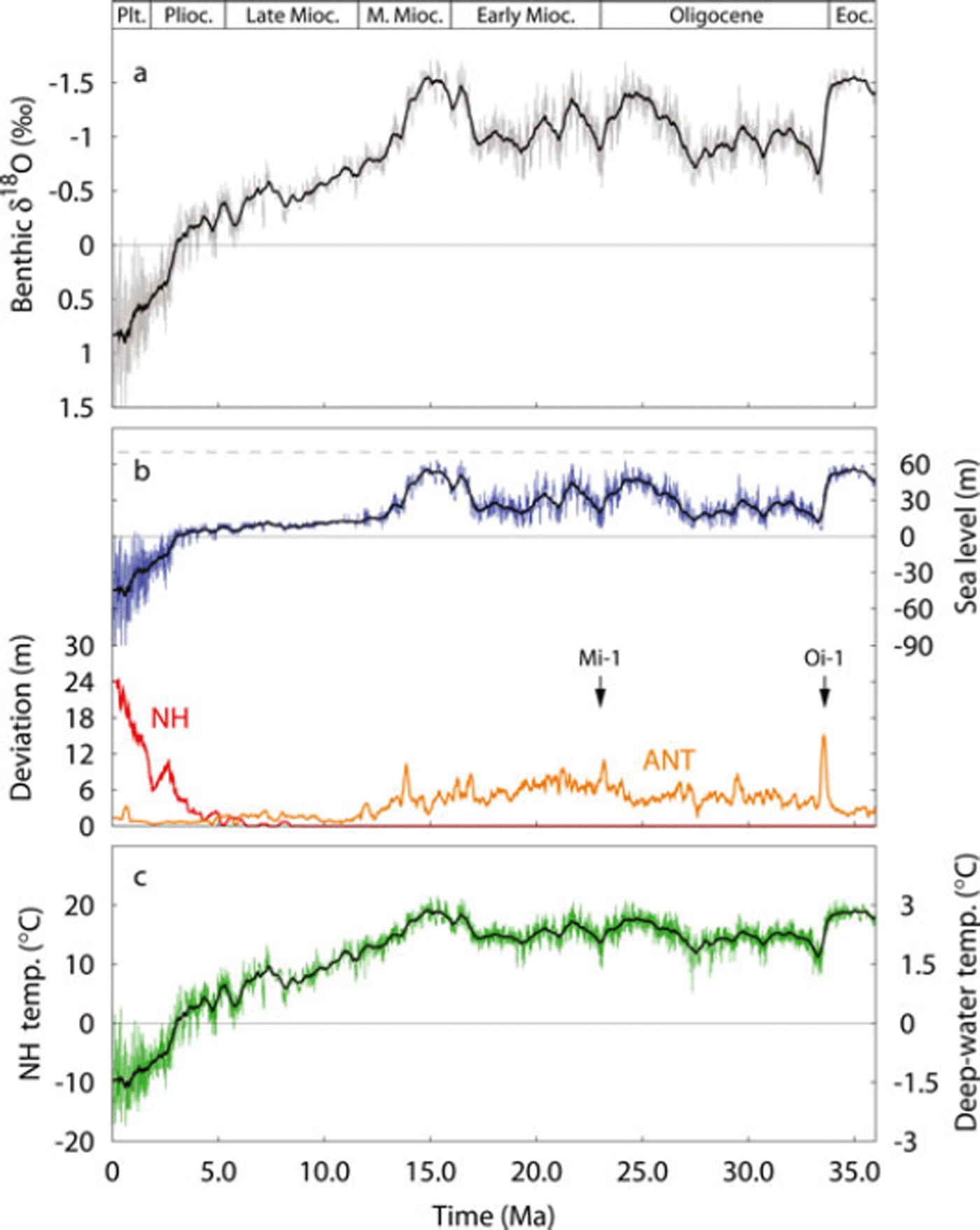
Fig. 4. (a) The Zachos benthic δ O data input (grey) over the past 35 Ma relative to PD (3.23‰). (b) Reconstructed sea level (blue) with the average standard deviation of the ice sheets calculated over 400 ka periods for the NH (red) and Antarctic (orange). (c) Reconstructed temperature (green). All values are relative to PD, and black lines represent the 400 ka running mean.
The lower part of Figure 4b shows the average standard deviation (a measure of variability) of NH and Antarctic ice-volume change (in m s.e.) over 400 ka periods. Clearly visible is the strong increase of NH glacial variability beginning at around 5 Ma, illustrating the waxing and waning of the EAS and NAM ice sheets in the Pleistocene.
Summarized in Table 3 are the tuning targets (or model constraints) for our simulations which are all met. Sea level at the LGM, however, is around 100 m below PD due to a lower amplitude in the Reference Zachos, Deickens and ZeebeZachos and others (2008) record compared to the LR04 forcing (Reference Lisiecki and RaymoLisiecki and Raymo, 2005). For the NH-only experiment, constraint 3 in Table 3 is therefore satisfied. Furthermore, the difference between modelled and observed δ18O remains within 0.005‰. Other prominent features in the history of the Antarctic ice sheet, such as the short drop in sea level around the Oligocene-Miocene boundary (Mi-1; –23 Ma) and the increase in ice volume in the mid- to late Miocene (15–10 Ma) (Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others, 2001) are well reconstructed by the model.
Table 3. Tuning targets for the full Cenozoic simulations

The two separate signals of the δ18Ob record are shown in Figure 5, illustrating the large variability in contributions of deep-water temperature and ice volume to the total δ18Ob signal. Although the variability is large, some distinct features can be recognized. Firstly, ice volume is the dominant signal during the Oligocene and the early to mid-Miocene, contributing to about 60% of changes in benthic δ18Ob.

Fig. 5. Percentage contribution of deep-water temperature (green) and ice volume (blue) to changes in benthic δ18Ob over the past 35 Ma, plotted as a 400 ka running mean.
Secondly, during the late Miocene (around 12–13 Ma), deep-water temperature becomes the major contribution to δ18Ob (–70%). During this time interval, the modelled EAIS reached its maximum extent, resulting in little change in sea level thereafter (see Fig. 4b). Since the benthic δ18Ob is still increasing during the late Miocene (see Fig. 4a), temperature lowers (see Fig. 4c) in order to satisfy the requirement that the difference between modelled and observed δ18O is minimized.
Thirdly, over the past 3 Ma, ice volume is again the dominant signal due to the waxing and waning of the NH ice sheets. The percentage contribution is only slightly larger than 50%, however.
The model outcome compares favourably with individual δ18Ob contributions (at the LGM) discussed in the literature. For example, Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others (2001) stated a contribution of the Antarctic and NH ice sheets of 1.2 and 1.1 ‰, respectively. Reference MillerMiller and others (2005) found a slightly lower contribution of the Antarctic ice sheet, 0.8–0.9‰, with a similar NH value of 1.2‰. These values are similar to the outcome of our model simulations, with contributions at the LGM of 1.0 and 0.8‰ relative to PD, respectively.
3.3. Equilibrium experiment
To further highlight the transition from Southern Hemisphere (SH-) to NH-controlled climate, we conducted an equilibrium experiment using a stepwise changing δ18O as input, with steps of 0.1 ‰. The experiment was initiated at a δ18O value of 1.1 ‰ then increased to a maximum value of 5.1 ‰, from which δ18O was reduced back to the initial value. Each δ O value was kept constant for 60 ka allowing the ice sheets to develop to a steady state, resulting in an equilibrium temperature and sea level corresponding to every δ18O value.
The experiment shows little hysteresis (Fig. 6; black line). An almost equal relationship between temperature and sea level is present compared to the transient experiment (blue boxes with bars). The shift from SH- to NH-dominated climate is well illustrated by the transition period centred around interglacial temperatures (∼0–8°C above PD). This indicates that interglacials are relatively stable periods compared to ice-volume change over the past 35 Ma, with the Antarctic ice sheet being in a more or less steady state and featuring minor to no glaciation in Eurasia and North America.
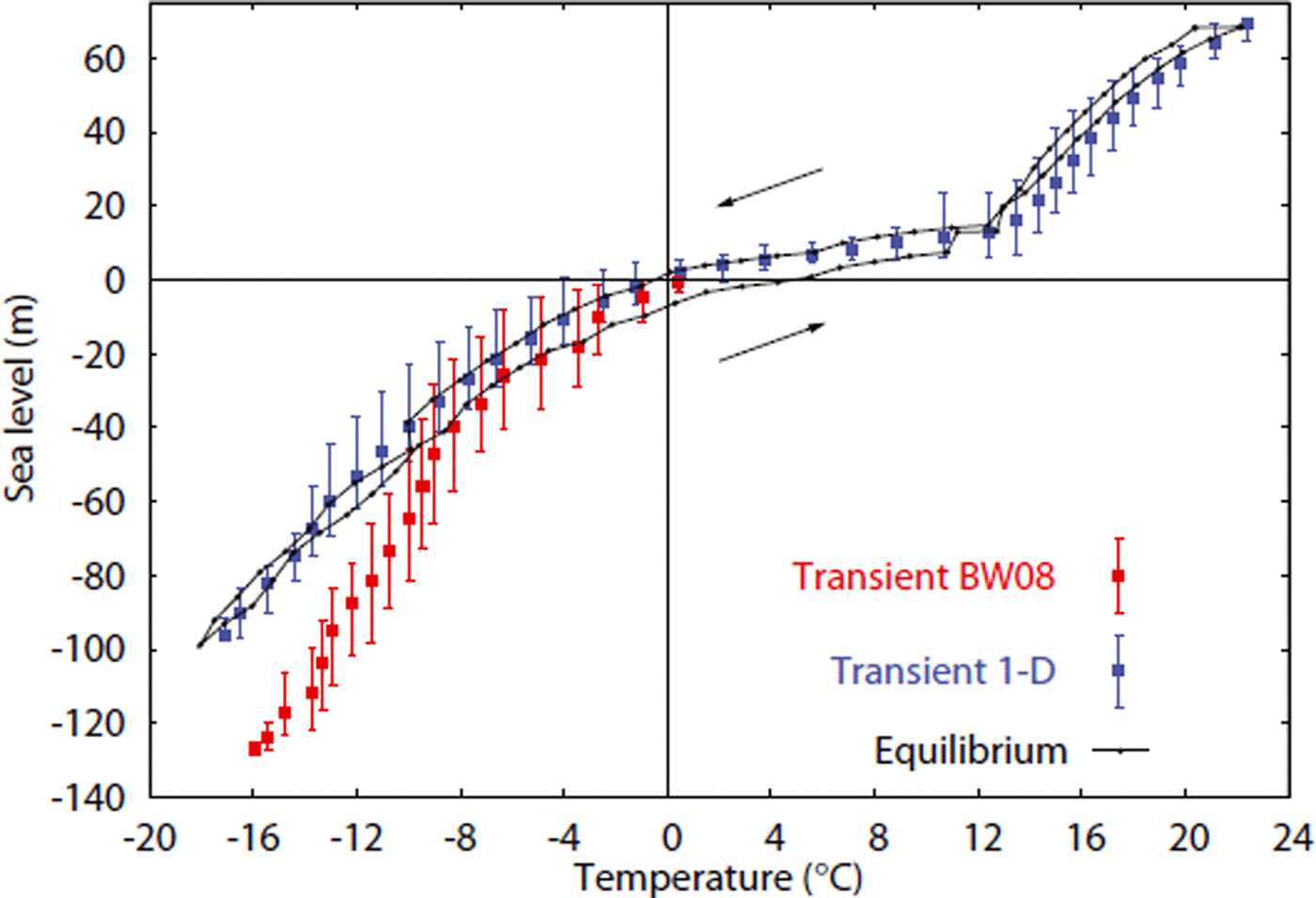
Fig. 6. The equilibrium experiment plotted for each δ18O step (black); arrows indicate the direction of stepwise changing δ18O . Average sea level and temperature from the transient simulations for each δ18O value (within a range of ±0.05‰): 1 Ma run of the 3-D model (red) and 35 Ma transient run of the 1-D model (blue). The bars indicate the range in sea level.
The red boxes with bars in Figure 6 represent the transient simulations with the 3-D ice-sheet model (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008) over the past 1 Ma. The results are similar to the 1-D model (in blue) for temperatures until ∼8°C below PD. For lower temperatures, however, there is a significant difference between the two models, for which the 1-D model results reveal lower temperatures for the same ice volume. These differences are mainly due to the inclusion of slightly different isotopic equations, such as Equations (2) and (3), and due to the simplified geometry. As was also mentioned by Reference Wilschut, Bintanja and van de WalWilschut and others (2006), the lack of hysteresis can also be ascribed to the simplified geometry of the 1-D model.
3.4. Sensitivity Tests
A large number of parameters in the model can be varied to satisfy the tuning targets implemented in our methods, which are shown in Table 3. Two parameters, i.e. the deep-water to surface-air temperature coefficient Adw and the temperature difference with the NH ice sheets, 5 TNH, were investigated for their sensitivity to model results.
Because the model includes ice sheets in both hemispheres, the outcome of the sensitivity experiments can be divided into two regimes: (1) before inception of NH ice sheets with higher than PD temperatures and (2) a regime including ice in the NH with temperatures (on average) lower than PD, roughly the past 3 Ma. As is implemented in our methods, the modelled δ18Ob closely follows the observed δ18Oobs record. In order to satisfy this requirement, each change in deep-water temperature or ice volume is compensated by its counterpart (see Equation (2) or (A3)).
This is also shown in Table 4; the rightmost two columns list the changes in contribution to δ18Ob (equal in magnitude and of opposite sign). For experiment A, we replaced the deep-water to surface-air temperature coefficient Adw by the values shown in the table. The changes are shown with respect to the result with a value of Adw = 0.20. For experiment B, the difference between Antarctica and the NH ice sheet, JTNH, was increased/decreased by 4°C. Changes are shown with respect to δTNH = –10 and –6°C for the EAIS and WAIS, respectively.
Table 4. Averaged changes of the two sensitivity experiments over the two periods

Experiment A: deep-water temperature
A topic which was also addressed with the 3-D model (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008) is the coupling between deep-water and surface-air temperature. This relationship is based on an idealized climate-ocean model that linearly relates the deep-water temperature to the 3 ka mean NH temperature; see Equation (4). Reference Bintanja and Van de WalBintanja and Van de Wal (2008) used a value of 0.20 for Adw, which we also adopted for the NH-only experiment described in section 3.1. Similar to the tests performed by Reference Bintanja and Van de WalBintanja and Van de Wal (2008), the 1-D model was tested with two additional values for Adw (0.15 and 0.25; experiment A) as depicted in Figure 7a.

Fig. 7. Sensitivity tests performed with the model shown as 400 ka running mean over the past 35 Ma. (a) Varying the deep-water to surface-air temperature coupling, NH temperature (top) and sea level (bottom) over the past 35 Ma. The default experiment with λ dw = 0.20 is shown in black. (b) Varying the temperature difference from the NH ice sheets. Values indicate deviations from the gradients shown in Table 1 (black line), δT NH = –12 and –8˚C (–4, green) and δT NH = –4 and 0˚C (+4, blue) for the EAIS and WAIS, respectively.
As can be seen in Table 4, changing the Adw value resulted in coherent changes in temperature and sea level (ice volume). The parameterization within the model is adjusted by changing Adw, therefore affecting the deep-water temperature calculation first. Since temperatures are calculated relative to PD, a lower Adw results in deep-water temperatures closer to PD, i.e. deep-water temperatures are lower and higher prior to and after 3 Ma, respectively.
In order to compensate for the changes in deep-water temperature contribution to benthic δ18Ob, both surface temperatures and ice volume counteract the deep-water temperature changes. In summary, a lower (higher) Adw leads to a decrease (increase) of deep-water temperatures prior to 3 Ma, resulting in higher (lower) surface temperatures and sea level, i.e. less (more) ice volume. After 3 Ma, the changes are reversed.
Experiment B: north-south temperature gradient
A second parameter which has been tested is the temperature difference from the NH ice sheets, δ TNH, indicating the difference between the Antarctic (or Greenland) and NH continental mean temperature reduced to sea level (without any ice). Although the values shown in Table 1 are selected from a realistic range, there is still some uncertainty related to this parameter. Three different sets of values for Antarctica have been chosen to test the sensitivity of the model output in steps of 4˚C, i.e. δT NH = –14 and –10˚C and δT NH = –6 and –2˚C as extreme values. Central values are shown in Table 1 : δT NH = –10 and –6˚C for the EAIS and WAIS, respectively.
The results with respect to the central values are presented in Figure 7b and clearly show that the separate regimes are also present for this experiment. Prior to 3 Ma the differences are quite large; for the past 3 Ma, however, changes in temperature and sea level are much smaller (Table 4). For the latter regime this is due to the limited variability of the EAIS and WAIS, as both have reached the continental margins prior to this period.
As can be seen in Figure 7b and Table 4, a reduction in ice volume is accompanied by an increase in temperature and vice versa (in contrast to experiment A). Changes prior to 3 Ma, however, are quite straightforward. Antarctic surface-air temperature is lower when the temperature difference δT NH is larger, i.e. more negative. Although precipitation is reduced due to a reduction in the moisture-holding content of the atmosphere, the accumulation increases (more snow) and ice volume is increased. To compensate for the increase in ice-volume contribution to benthic δ18Ob, deep-water and surface temperatures are higher.
The differences over the past 3 Ma, when temperatures are generally below PD, are mainly due to a small reduction in EAIS volume due to a change in accumulation as a result of lower (or higher) temperatures. In summary, a larger (smaller) δT NH increases (decreases) ice volume prior to 3 Ma, resulting in an increase (decrease) in ice-volume contribution to δ18Ob. This is compensated by an increase (decrease) in deep-water and surface-air temperatures.
The choice for the parameters used in the standard experiment is based on our tuning targets. We used λ dw = 0.15 because of a better agreement with Plio–Pleistocene sea-level and NH temperature variations. Furthermore, the choice for δT NH is less significant since its influence is mostly limited to Antarctic ice volume (for which the PD ice volume and a strong increase at Oi-1 are satisfied in all cases). The intermediate values of δT NH, –8 and –4˚C for East and West Antarctica, respectively, are therefore used.
4. Discussion
A reconstruction of global sea level and NH surface-air temperature over the past 35 Ma has been presented. Following the inverse procedure introduced by Reference Bintanja, van de Wal and OerlemansBintanja and others (2005a) with benthic δ18Oobs as input, we have separated the δ18Ob signal into an ice-volume and deep-water temperature contribution.
The results of the 1-D model, however, can be affected by several model parameters such as the deep-water to surface-air temperature coupling (λ dw) and the difference between the Antarctic and NH continental temperature (δT NH). It has been shown that both parameters have a significant influence on the individual contributions of ice volume and temperature to the δ18Ob signal. The largest differences in model results were found prior to 3 Ma. Changes in the contribution of ice volume were about 10%, which are essentially changes in Antarctic ice volume as NH ice sheets had not yet developed.
Due to the simple geometry and the use of a fixed-grid ice-sheet model, the modelled Antarctic ice sheets showed little sensitivity to sea-level change. Tests have been carried out using a stretching grid, but over the past 35 Ma differences were very small compared to the fixed-grid simulations. For these long-term changes, the low sensitivity is therefore not a concern for Antarctic ice-volume evolution.
Over the past 3–5 Ma, however, Antarctic ice volume stays more or less constant, which is not in agreement with several other studies (e.g. Reference Conway, Hall, Denton, Gades and Wadding-tonConway and others, 1999; Reference HuybrechtsHuybrechts, 2002; Reference Pollard and DeContoPollard and DeConto, 2009). The large sea-level fluctuations during the Pleistocene allowed the grounding line of the WAIS to migrate through the shallow Ross and Weddell Seas (Reference Conway, Hall, Denton, Gades and Wadding-tonConway and others, 1999), increasing its volume significantly during glacial maxima. Although sea-level and temperature fluctuations over the Plio–Pleistocene are mainly caused by changes of the NH ice sheets, the simple geometry of the Antarctic ice sheets does not allow for large changes in West Antarctica. According to other modelling studies, differences in Antarctic ice volume could be of the order of 10 m of sea level (Reference HuybrechtsHuybrechts, 2002). For the Pleistocene, therefore, a significant uncertainty range ( 10%) can be accounted for during glacial periods.
4.1. Comparison of reconstructed sea level
Although there is some uncertainty related to our short-term changes, over the past 35 Ma our reconstruction of sea level and temperature is comparable to observations and other studies. For example, Reference OerlemansOerlemans (2004b) used a continuity model for the Antarctic ice sheet to separate the deep-water temperature and ice-volume signals from the benthic δ18Ob record. Overall the methodology is quite different, but in this study an axisymmetric model is also used with a sloping bed.
The method of Reference OerlemansOerlemans (2004b) is based on a linear relation between δ18Ob and both deep-water temperature and ice volume:
where a is related to the deep-water temperature for δ18Ob = 0, when the stable oxygen isotope ratio is at the VPDB standard level. From Equation (11), the deep-water temperature is derived as a function of δ18Ob (input) and ice volume (calculated with the model). Furthermore, the Antarctic temperature is related to the deep-water temperature (Reference OerlemansOerlemans, 2004b, equation (7)) as a function of Δ, a constant temperature difference between the deep-sea and Antarctic continent, and to an additional feedback parameterization between ice sheet and climate.
For a more straightforward comparison with our methodology, Equation (11) can be restated relative to PD (similar to the treatment of Equation (A3) in the Appendix):
When comparing Equations (12) and (A4), the biggest difference is the constant c; it is assumed that the isotopic content of the ice-sheet and ocean volume remains constant throughout the Cenozoic. Nevertheless, as shown in Table 5, the constants are similar to those used in our study.
Table 5. Comparison of model constants used in this study and by Reference OerlemansOerlemans (2004b)

A comparison of both reconstructions is shown in Figure 8, for which we used the original compilation by Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others (2001) interpolated to 0.1 ka as input for a better comparison with Reference OerlemansOerlemans (2004b) (who used the same input smoothed to a 100 ka resolution). From the Eocene to the middle Miocene (–10Ma), our reconstructed Antarctic ice volume (blue curve in Fig. 8b) is very similar to that of Reference OerlemansOerlemans (2004b) for Δ = 9°C (shown in orange). The deep-water temperature reconstructions, however, are less similar as shown in Figure 8a. In particular, 1-D model temperatures are significantly lower during the Oligocene (33–26 Ma) and mid-to late Miocene (15–4 Ma). The average trend over the latter period, however, is comparable, with approximately equal temperatures at 15 and 4 Ma.
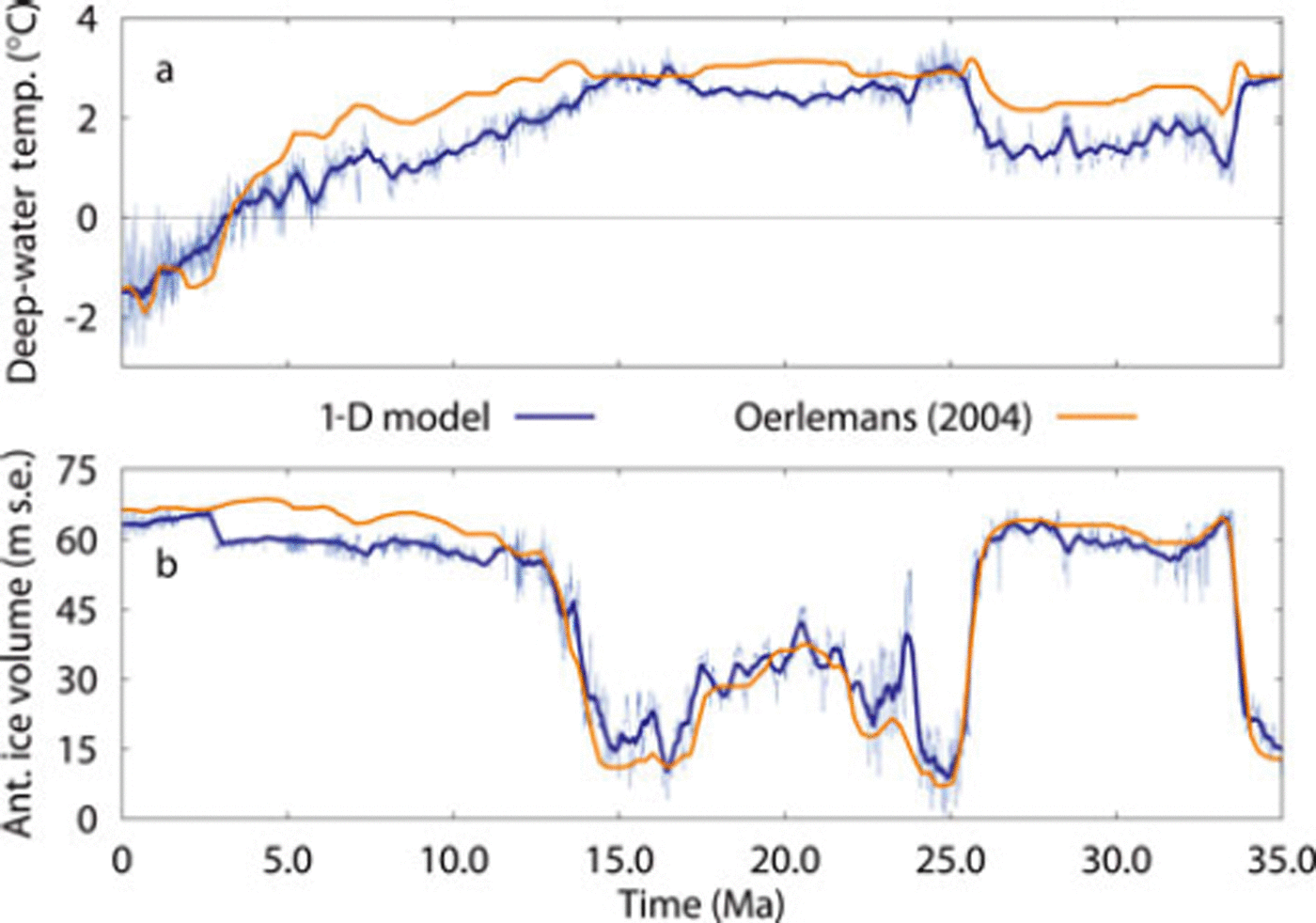
Fig. 8. Reconstructed (a) deep-water temperature relative to PD and (b) Antarctic ice volume of the 1-D model (blue). The dark blue curve is the 400 ka running mean, and the results from Reference OerlemansOerlemans (2004b) for Δ = 9˚C are in orange.
In addition to the comparison with other modelling results, Figure 9a shows a comparison with two long-term records over the past 35 Ma by Reference Müller, Sdrolias, Gaina, Steinberger and HeineMuller and others (2008) (red) with error envelope and Reference MillerMiller and others (2005) (green). The Muller curve shows a reconstruction of the effects of changes in crustal production, sediment thickness, ocean-basin depth and area on sea level, and illustrates sea-level changes owing to long-term effects other than ice-volume fluctuations. Although the mean (thick red line) curve does not show much variability over the past 35 Ma, the error envelope is significant and shows that there is still much debate about past sea-level height. Nevertheless, the volume of the ocean basin only changes by a maximum of ∼1% (Reference Müller, Sdrolias, Gaina, Steinberger and HeineMuller and others, 2008) and therefore shows that our assumption of a constant ocean depth and area is acceptable.

Fig. 9. Reconstructed sea level (blue) compared with other sea-level reconstructions: (a) over the past 35 Ma with sea-level curves of Reference Müller, Sdrolias, Gaina, Steinberger and HeineMüller and others (2008) in red with error envelope and Reference MillerMiller and others (2005) in green; and (b) over the past 0.5 Ma with Red Sea basin sediment δ18O records (Reference RohlingRohling and others, 2009) and New Guinea and Barbados coral reef data (Reference Lambeck and ChappellLambeck and Chappell, 2001).
The Reference MillerMiller and others (2005) sea-level record (in green) prior to 9 Ma is based on ‘backstripping’ a New Jersey stratigraphic record, which mainly accounts for the effects of sediment compaction, loading and water-depth variations. Changes in Antarctic ice volume are taken into account, but are smaller than the 1-D model simulations (blue curve). The record shows strong variability and, prior to 10 Ma, seems to agree more with the record of Reference Müller, Sdrolias, Gaina, Steinberger and HeineMuller and others (2008) than with our sea-level curve derived from ice volume.
Over the past 10Ma the similarities are evident. Over this period, however, the Reference MillerMiller and others (2005) record is directly derived from δ18O using a scaling of 0.1 ‰ per 8 m and correcting the data prior to 2.5 Ma by 0.5‰ due to deep-ocean cooling. This is inconsistent with our findings as shown in Figure 5. Nonetheless, it is not surprising that both records show a coherent drop in averaged sea level over the past 5 Ma.
A completely independent comparison can be seen in Figure 9b, which shows past sea-level changes derived from Red Sea sediments (Reference RohlingRohling and others, 2009) and coral reef data from New Guinea and Barbados (Reference Lambeck and ChappellLambeck and Chappell, 2001). In terms of timing of glacial maxima, i.e. minima in sea level, the agreement is evident although the comparison for Termination V(–0.42 Ma) has improved with respect to a previous reconstruction (Reference SiddallSiddall and others, 2003). The amplitude of our reconstructed sea level (blue curve) is, however, smaller for all past terminations, mainly due to the small amplitude in the Reference Zachos, Deickens and ZeebeZachos and others (2008) δ18O record.
5. Conclusions
We have presented a full ice-volume reconstruction, mutually consistent with NH surface-air temperatures and benthic δ18Ob over the past 35 Ma, using a consistent method to derive the ice volume and temperature signal from benthic δ18Ob records. The method has worked well for a combination of five ice-sheet models representing glaciation of all the major ice sheets which existed during the Cenozoic.
The main result of our 1-D ice-sheet model simulation over the past 35 Ma shows that the contributions of ice volume and deep-water temperature to the benthic δ18Ob data exhibit large variations and cannot be assumed constant. Moreover, the results show a shift from a climate dominated by SH ice sheets to one dominated by NH ice sheets over the past 35 Ma, and reveal that the relationship between sea level and temperature is not constant with time.
Furthermore, it is shown that the 1-D ice-sheet model performs in line with the 3-D model results presented in Reference Bintanja and Van de WalBintanja and Van de Wal (2008) over the past 4 Ma and agrees well with observed sea-level records. The ice-sheet model, however, is a simplified representation of an actual ice sheet and has several limitations such as the unrealistic geometry, which does not support the merging of ice sheets and the formation of ice shelves. A more in-depth investigation of the associated ice-sheet dynamics, climate and sea-level changes will be presented in a future study, when we apply the same methods to the 3-D model (Reference Bintanja and Van de WalBintanja and Van de Wal, 2008) including ice-sheet models for Antarctica and Greenland.
Acknowledgements
Financial support was provided by the Netherlands Organization of Scientific Research (NWO) in the framework of the Netherlands Polar Programme (NPP). Thanks are due to colleagues of the IMAU and two anonymous reviewers for providing useful comments leading to improvements in the manuscript.
Appendix: Separating The δ18O Signal
The separation of the benthic δ18O record into an ice-volume and temperature signal is based on mass conservation of the stable oxygen isotope 18O.
First, we consider a simple mass conservation relation between the ratio of this isotope in ice and in the ocean water:
where V
o and Vi are the ocean and ice volume km3 water equivalent), respectively, and δ18Oo and ![]() are the ocean-water and mean ice-sheet δ18O, respectively.
are the ocean-water and mean ice-sheet δ18O, respectively.
Secondly, to include the total benthic δ18Ob signal, we need to subtract the deep-water contribution from the benthic data to determine the ocean-water signal and substitute this into Equation (A1):
The value of γ is adopted from Reference Duplessy, Labeyrie and WaelbroeckDuplessy and others (2002), in which they showed a linear relation between benthic δ18O and deep-water temperatures with a slope of –0.28‰ °C−1 .
So far we have considered absolute values of the above variables. We want, however, to calculate δ18Ob with respect to PD. To do so, first we rewrite Equation (A2):

which shows the separation of the ice-volume signal (first term on the right-hand side) and deep-water signal (second term on the right-hand side) of the benthic isotope signal δ18Ob. Secondly, Equation (A3) is restated relative to PD:
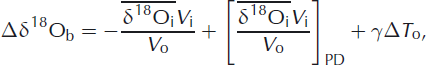
where Δ denotes values relative to PD. Furthermore, V o is calculated as the PD depth of the ocean (D o = 4 km) minus the calculated global sea level (ΔS) times the area of the world’s ocean (O area), which is assumed to remain constant at 3.62 × 108 km2:
















