Introduction
Blowing and drifting snow influences human activities in various ways. For example, in mountainous regions snow-drifting is a key factor in the formation of slab avalanches; the quality of avalanche-danger mapping and land-use planning depend significantly on the correct assessment of snow-redistribution by drifting in the avalanche-release zones.
Most previous work on this topic focused on field experiments (Reference SchmidtSchmidt, 1980; Reference TakeuchiTakeuchi, 1980) and wind-tunnel studies (Reference Naaim-BouvetNaaim-Bouvet, 1995). Only a few attempts have been made to simulate snowdrifting effects numerically (Reference Uematsu, Kaneda, Takeuchi, Nakata and YukumiUematsu and others, 1989; Reference Liston, Brown and DentListon and others, 1993; Reference SundsbøSundsbø, 1997). These numerical models are restricted to a two-dimensional case. A three-dimensional simulation was carried out by Reference Uematsu, Nakata, Takeuchi, Arisawa and KanedaUematsu and others (1991) for a simple topography. Most of the field studies were undertaken on flat terrain with a homogeneous wind field. Attempts to measure snowdrifting and its distribution in mountainous terrain are equally scarce (Reference FöhnFöhn, 1980; Reference Föhn and MeisterFöhn and Meister, 1983; Reference Schmidt, Meister and GublerSchmidt and others, 1984). In all these cases only a few or no wind data are available.
This study is divided into two parts: (1) presentation of a numerical model For snowdrifting; (2) comparison between numerical simulations and field measurements.
Numerical Model
Physical Basis
Conceptually, drifting snow is a turbulent multi-phase flow that consists of a continuous and dispersed phase. For each phase, air as the continuous phase and the snow particles as the dispersed phase, the principles of mass and linear momentum balance ought to be formulated. However, for extended areas with a complex topography, the computational effort becomes too great. Therefore, we should restrict ourselves.
It is common to distinguish between three transport modes in snowdrifting; creeping, saltation and suspension. Saltation and suspension are responsible for the main mass transport. Hence, creeping is not included in the model. Figure 1 shows a schematic diagram of the processes involved in the drift system.

Fig. 1. Schematic diagram of the processes involved in the drift system. The symbols denote: wind speed at the height z, U(z); shear stress, τ; airborne shear stress, τa; grain-borne shear stress, τg; aerodynamic entrainment, Qcae; ejection rate, Qcej; deposition rate, Qcd; turbulent entrainment, Qct; settling rate due to gravity, Qcs; horizontal mass flux, Qm; feedback, F.
The driving force is the wind field, where the shear stress, τ, is an index for the av ailable power. The snowpack will be affected by the airborne shear stress, τa, and the grain-borne shear stress, τg. τa determines the aerodynamic entrainment, Q cae, which is responsible for the initiation of drifting. After initiation, the drastic increase of drifting particles is determined by particle impacts, which exercise a shear stress τg on the snowpack. These impacting particles eject other particles, denoted as Q cej in Figure 1. Because of the interaction between the particles and the wind field within the saltation layer, the drifting particles will be accelerated whereas the flow will be decelerated and so τg increases, whereas τa decreases, as they must sum up to τ:
Hence, the importance of aerodynamic entrainment decreases, whereas the importance of particle impacts increases until a steady state is reached. The drifting snow particles extract a certain amount of momentum from the flow. Experiments show that this effect is similar to an increase of the effective roughness height (Reference BagnoldBagnold, 1941). Due to the increasing roughness height, the wind speed in the boundary layer decreases, jumping particles gain less energy from the wind field and consequently fewer particles will be ejected due to particle impacts. This mechanism serves as a negative feedback and is responsible for achieving a steady state. Due to the turbulence of the flow, a certain number of particles go into suspension. In the figure, this part is denoted as Qct. In all cases, gravity acts as a counter balance on the particles in saltation as well as those in suspension and accounts for the settling rate Q cs.
Mathematical Formulation
Suspension Mode
In the suspension mode, the particle concentration is small and simple mixture theory is applicable. So we solve the continuity. Equation (2), and Reynolds averaged Navier-Stokes equations Equation (3) for the air. For the snow particles in suspension as well as for the precipitation an additional scalar equation for the concentration is introduced Equation (4).



Here u and u′ denote the mean velocity vector and the velocity fluctuations of the air, respectively. In a similar way c and c′ denote the mean concentration and the fluctuation part. As long as the concentration of snow in suspension is small, the density, ρ, of air can be used, g denotes the gravity vector. Averages involving products of fluctuating quantities are overlined. We assume that the particle velocity is equal to up = u + Wf, where Wf is the free-fall velocity of a particle. In Equation (3) the viscous shear-stress terms are dropped. For the turbulent-flux terms, we use the eddy-viscosity hypothesis and the eddy-diffusivity hypothesis, which means that all turbulent fluxes are linearly related to the mean gradients. For the Reynolds stress, we write:

and for the Reynolds flux:
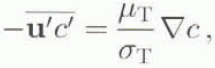
where δ is the Kronecker tensor. For the necessary closing of the turbulent equation we use the k – ε equations,


where k and ε stand for the turbulent kinetic energy and the dissipation, respectively, P denotes the shear production of turbulent energy and G the production due to buoyancy. μeff represents the effective viscosity defined by:

In the k – ε model, it is assumed that turbulent viscosity. μT is given by

c1, c2, c3, cμ, σT and σk/ε are constants given by Reference RodiRodi (1980).
For the boundary condition of the wind field at the snow-pack surface, the well-known wall-function is used, where we modify the effective roughness height. It is reasonable to assume that the roughness height, z 0, depends on the saltation height, hs , and concentration, cSa within the saltation layer
However, only a little is known about this relationship and almost all authors drop the dependence on the concentration, e.g. Reference OwenOwen (1964). This might be justified as long as saturation is assumed. In a first attempt to include the concentration here we use the expression

where w0 is the vertical lift-off velocity of a particle and d p is the particle diameter. So, depending on the panicle concentration, the roughness height increases until a maximum value is readied. This maximum value is similar to that given by Reference OwenOwen (1964). In the literature the values for the constant C 0 vary from 0.013 to 0.18. The part depending on the concentration is motivated by Reference LettauLettau (1969), who gave an expression for the roughness height in the case of fixed obstacles on a plane.
Saltation Mode
The saltation mode will be described by two equations. The first one is for the volume-averaged mass balance of the snow (Equation (13))

where A i are the areas of the vertical sides of the control volume V, Qcs is gravitational settling out of the suspension layer and Qct is the turbulent entrainment of snow into the suspension layer. These source terms are given by
Here, c− and c+ denote the volume fraction of snow particles just below and above the boundary between the saltation and suspension laver respectively. A t is the area of that boundary. Wf is the particle free-fall velocity and the fluctuation velocity, W′, is estimated as
Until now, little has been known about the ejection rate, the aerodynamic entrainment and the deposition rate for snow. Reference Anderson and HaffAnderson and Haff (1991) gave some splash functions for sand which are based on computer simulation. To adopt these “ansatzes” for snow is critical as far as sand is cohesion-less, whereas the properties of the snowpack depend strongly on particle cohesion. For the aerodynamic entrainment rate, Qcae , the difference between snow and sand might be small, so the expression
which was given by Reference Anderson and HaffAnderson and Haff (1991) can be used. Certainly, differences are expected in the threshold shear stress, τc, and the constant of proportionality. ζ. In the formula above, V p is the particle volume and As is the surface area of the snowpack.
It is reasonable to assume that the ejection rate is a function of kinetic energy of the impacting particle, E
imp, and the binding energy of the surface particles, E
B. Since little is known about the distribution function of impact energy, we work with its averaged value, ![]() . In addition, we introduce the fraction of particles whose actual impact energy exceeds the threshold value, EB
; it is a function of both
. In addition, we introduce the fraction of particles whose actual impact energy exceeds the threshold value, EB
; it is a function of both ![]() and
and ![]() . Then, the ejection rate can be expressed as follows
. Then, the ejection rate can be expressed as follows

where ![]() is the number of grains ejected per particle impact. In our state, we assume that the impact energy, Eimp
, has a normal distribution and the deviation is
is the number of grains ejected per particle impact. In our state, we assume that the impact energy, Eimp
, has a normal distribution and the deviation is ![]() and
and ![]() the probability that Eimp
exceeds EB
. cV/ti
gives the number of impacts per second and here ti
denotes the mean jump time of a particle. The number of ejections is determined by the energy balance
the probability that Eimp
exceeds EB
. cV/ti
gives the number of impacts per second and here ti
denotes the mean jump time of a particle. The number of ejections is determined by the energy balance

where E0 and Ee are the kinetic energy of the rebounding particle and ejected particle, respectively. E D is the energy dissipated in the snowpack.
The deposition rate depends on the probability of a particle to rebound, P r:
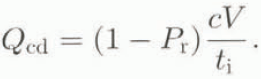
The second equation for the saltation mode is a momentum balance

If we know the rate of momentum loss due to particle impacts and ejection, ![]() , the momentum equation can be used to determine the airborne shear stress, τa. This equation describes the balance between the force necessary to accelerate the mass of the rebounding and ejected snow particles m
Ar\e in the time of a particle jump t
i from the start velocity
, the momentum equation can be used to determine the airborne shear stress, τa. This equation describes the balance between the force necessary to accelerate the mass of the rebounding and ejected snow particles m
Ar\e in the time of a particle jump t
i from the start velocity ![]() to the impact velocity
to the impact velocity ![]() , and shear stress τ at the surface of the saltation layer, and the airborne shear stress Ta at the top of the snowpack, respectively. In the equation above, subscripts
, and shear stress τ at the surface of the saltation layer, and the airborne shear stress Ta at the top of the snowpack, respectively. In the equation above, subscripts ![]() mark velocity components parallel to the surface of the snowpack and ϕ is the slope angle of the snowpack. mA
is the sum of the mass of the particle, mAr
, rebounding during the time ti
and the mass of the particles, mAe
, ejected during that time.
mark velocity components parallel to the surface of the snowpack and ϕ is the slope angle of the snowpack. mA
is the sum of the mass of the particle, mAr
, rebounding during the time ti
and the mass of the particles, mAe
, ejected during that time.
Thus far in the analysis, the particle velocities in the saltation layer are unknown. To close the obtained system of equations, we assume that all particle velocities are proportional to the wind speed at the upper surface of the saltation layer.
The whole model is implemented in the commercial flow solver CFX4.1, a program based on the finite-volume technique. The program allows all the necessary procedures for the drift simulation to be written in so-called FORTRAN USER ROUTINES. In order to evaluate the snowpack, we use a transient grid that is adjusted to the new snow depth at regular time intervals.
Field Observations and Measurements
During the winter of 1996-97, a test site 2 km north of the Institute building at Weissfluhjoch, Gaudergrat ridge (2305 m a.s.l.), was equipped with instruments to measure meteorological, snow and wind-field parameters. The ridge has a rather sharp crest — the slope angles ranges from 28° to 38° — and might be regarded as prototypical of Alpine topography. The mean wind direction during strong precipitation periods is more or less northwest and so perpendicular to the crest line.
Before and after snowdrifting periods, the volume and mass of snow were determined by measuring snow depth along equidistant lines across the crest, roughly 8.5 m apart and over 200 m long. Soundings were taken at 4 m intervals along these lines. Thus, every field campaign resulted in around 300 data points. All measurement points were marked by thin bamboo stakes. In this manner, uncertainties in the depth measurements due to the small-scale topography could be minimized. To convert to snow mass, density measurements were also made at several points. Through these measurements, the recently eroded and deposited snow mass could be evaluated and mapped.
To verify the numerical model, it is also necessary to get an impression of the wind field around the crest. We therefore installed five wind masts in the surrounding area and made measurements of the wind-speed profiles during drifting periods. Then the measurements were compared with the simulated wind field.
In the first simulation, it could be observed that the simulated wind field differs significantly from the measurements. Also, in contrast to the snow measurements, the simulated erosion area extended over the crest into the leeward side. One reason for this phenomenon was the poor resolution of the grid at the crest. The 25 m grid spacing of the digital topography model DHM25 leads to significant smoothing of the rather sharp and narrow crest. Because of this, the recirculation and the deposition zone start some distance down the slope. This explanation is supported by the erosion pattern observed by Reference Föhn and MeisterFöhn and Meister (1983). Their figure shows the erosion/deposition for a rounded crest. The erosion area also extends into the leeward slope.
Hence, in a second step, we refined the DHM25 in the surroundings of our test site with the aid of additional points on a 5 × 5 m grid. After this procedure, the features of the crest could be resolved quite well. The comparison between wind-field measurements and simulations done with the improved grid gives satisfactory results.
A simulation of the snow distribution for an area comprising the Gaudergrat test site is shown in Figure 2. The simulated snow depth, H, is normalized against the initial snow depth, H 0. This figure shows the potential erosion-deposition areas. In this case, a northwesterly wind direction was assumed. Along the upwind face, we assumed a logarithmic wind profile with a wind speed of 6 m s−1 at 5 m above the snowpack and a precipitation rate of 10−4 kg m−2 s−1. The figure also gives an impression of the test site.

Fig. 2. Simulation of snowdrift under wind from the northwest. The contour interval is 20 m. The white points mark positions of the masts for the wind and the meteorological measurements and our hut. Also shown are the corners of the area where the soundings were made. They are marked by black points (topographic data from DHM25: ©Swiss Federal Office of Topography).
Figure 3 shows a comparison of a measured new snow depth, HN, and a corresponding simulation for one period. The new snow depth is normalized against the reference depth, H ref, which corresponds to the new snow depth in an undisturbed area. The measurements show great variability but also some trends could be seen. One can see the erosion area on the windward slope near the crest line, at the ridge the formation of a cornice, and just behind the crest an area where the snow depth is less than the reference depth. Downslope one can find areas, where HN is two or three times Href , and again areas where it is less than Href , It can also be seen that local terrain features cause large differences in the erosion and deposition patterns. The simulation does not show this variability but does reproduce some of the characteristics. So these first results are encouraging.

Fig. 3. Comparison between measured new snow depth and a simulation for the drift period from 4 to 6 April 1997, with winds from the northwest. The black points mark the position of the masts and of the hut (topographic data DHM25: ©Swiss Federal Office of Topography ).
One of the reasons for the differences between the measurements and the simulation might be the assumption of a homogeneous snowpack in the simulation. In reality, this assumption can be justified only for the new snow layer. If the old snowpack is included, variations in the threshold shear stress have to be taken into account, but this is a poorly known feature of a snowpack property.
A second reason is because of the wind-field simulation. Figure 4 shows a excerpt from the time plot of the wind speed components u, v, and w for the drifting period from 4 to 6 April 1997. Here, the great variability in all three components can be seen, expressing the high turbulence of the wind field during a storm. If we assume that the drifting snow mass depends on a power of the wind speed ![]() , short gusts are responsible for a great amount of snow redistribution. At this point, we should mention that one characteristic of all numerical turbulence models is time-averaging. So the gusts which can be observed in reality will be averaged in the simulation. This is a potential source for significant errors in numerical simulations (Reference CastelleCastelle, 1995).
, short gusts are responsible for a great amount of snow redistribution. At this point, we should mention that one characteristic of all numerical turbulence models is time-averaging. So the gusts which can be observed in reality will be averaged in the simulation. This is a potential source for significant errors in numerical simulations (Reference CastelleCastelle, 1995).

Fig. 4. Time plot of the wind-speed components u (east), v (north) and w (vertical) at the top of Gaudergrat ridge at 3 m above the snow surface (10 s averages).
Concluding Remarks
A numerical model for drifting and blowing snow has been developed. Comparison between a first numerical simulation and field measurements demonstrates the problems involved in the simulation of complex terrains. The primary modelling difficulties are that grid resolution must match the length scale of the terrain and the wind field at the boundary of the computational domain needs to be interpolated correctly. Another critical point is the poorly known interaction between the air and the snow particles, e.g. how the effective roughness height depends on particle concentration. Nevertheless, the preliminary results hold promise that numerical simulations of snowdrifting will develop into a powerful tool for land-use planning and maybe avalanche forecasting once the problems mentioned above have been solved.
Acknowledgements
I am indebted to C. Fierz, M. Hiller, D. Issler, G. Krüsi, R. Meister and P. Weilenmann, as well as the staff of the mechanical workshop for their help in preparations for the field measurements. Similarly, I am grateful to C. Camponovo, S. Harvey, C. Marty, R. Mullins and K. Plattner for their assistance in the field, and F. Naaim-Bouvet and M. Naaim for fruitful discussions during my stay at CEMAGREF in Grenoble.
This work was supported by the Swiss Federal Office of Education and Science under the contract OFES 93.0082 as part of the European “Human Capital and Mobility” project “Contribution to avalanche dynamics with the aim of mapping hazardous areas”, contract CE CHRX-CT 93-0307.






